八年级数学下册课件-18.2.3 正方形1-人教版(共20张ppt)
文档属性
| 名称 | 八年级数学下册课件-18.2.3 正方形1-人教版(共20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 673.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-05 19:07:35 | ||
图片预览

文档简介
课题:正方形的性质(3)
难点:正方形性质和三角形有关知识结合的综合应用
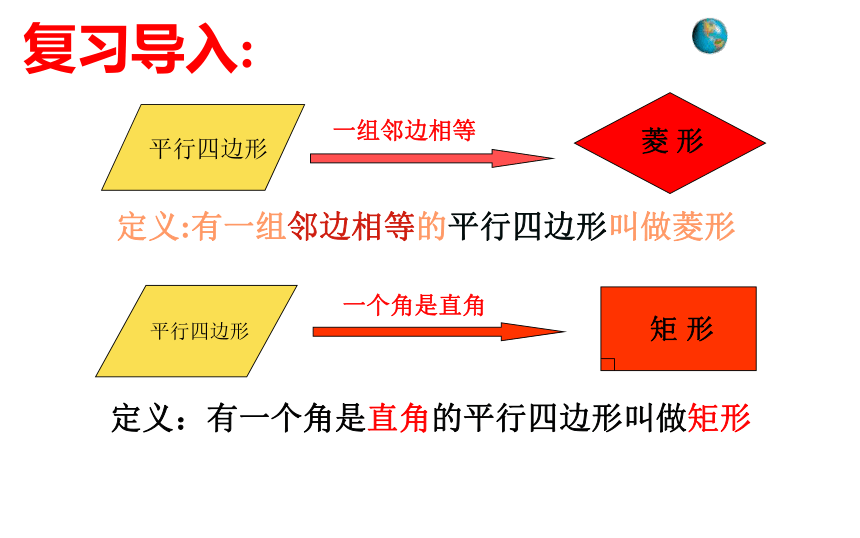
平行四边形
菱 形
定义:有一组邻边相等的平行四边形叫做菱形
平行四边形
一个角是直角
矩 形
定义:有一个角是直角的平行四边形叫做矩形
一组邻边相等
复习导入:
矩 形
正方形
〃
〃
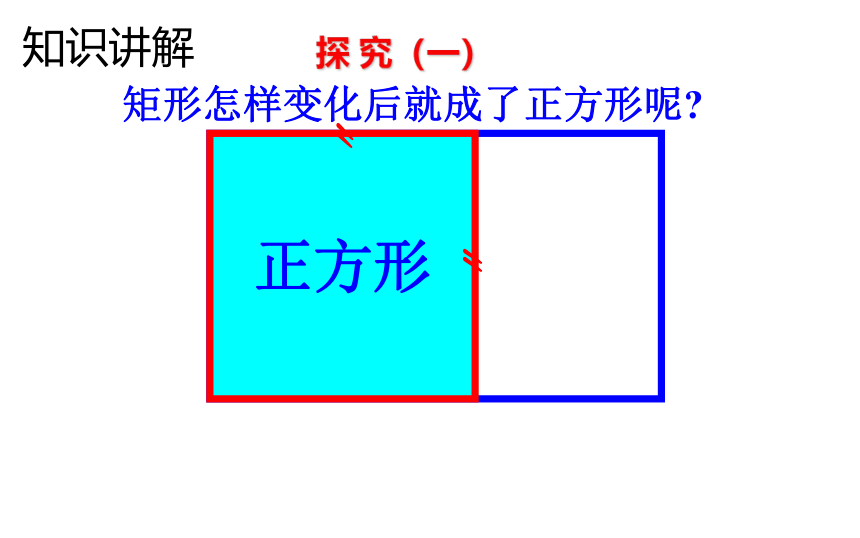
矩形怎样变化后就成了正方形呢?
探 究(一)
知识讲解
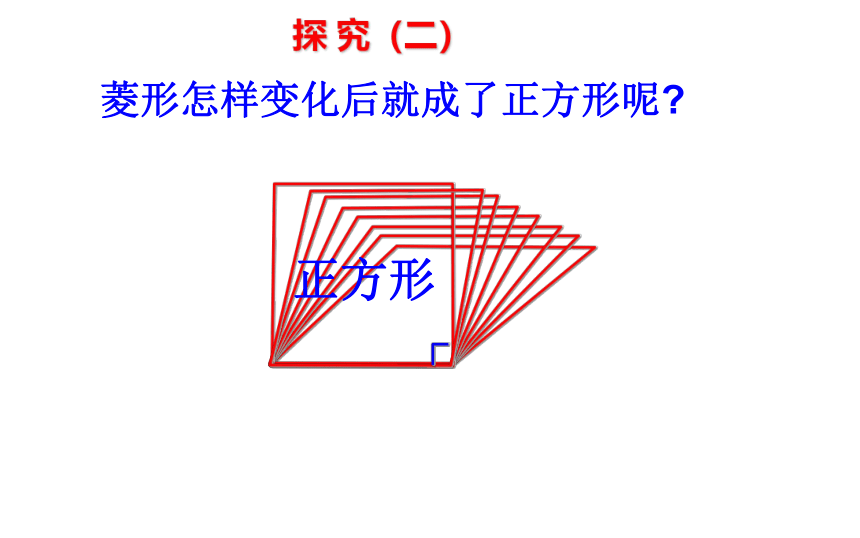
探 究(二)
菱形怎样变化后就成了正方形呢?
正方形
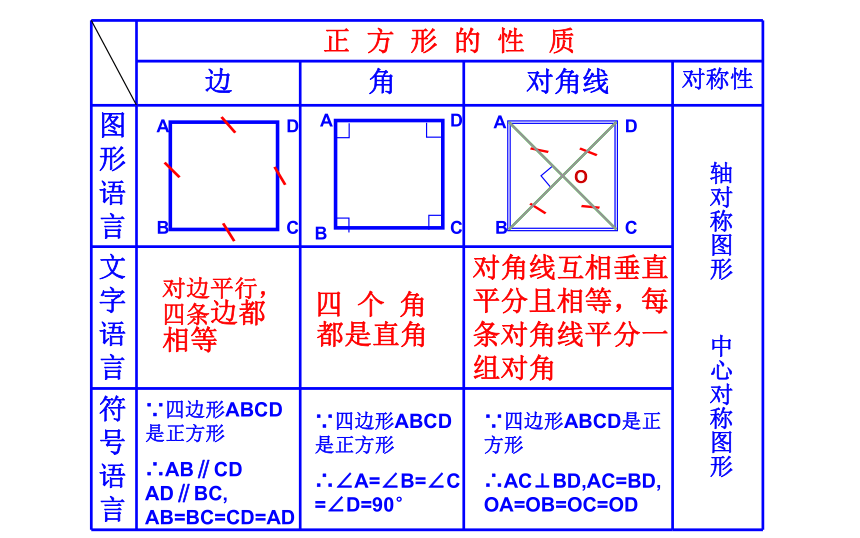
正 方 形 的 性 质
边
角
对角线
对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行, 四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD 是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形 中心对称图形
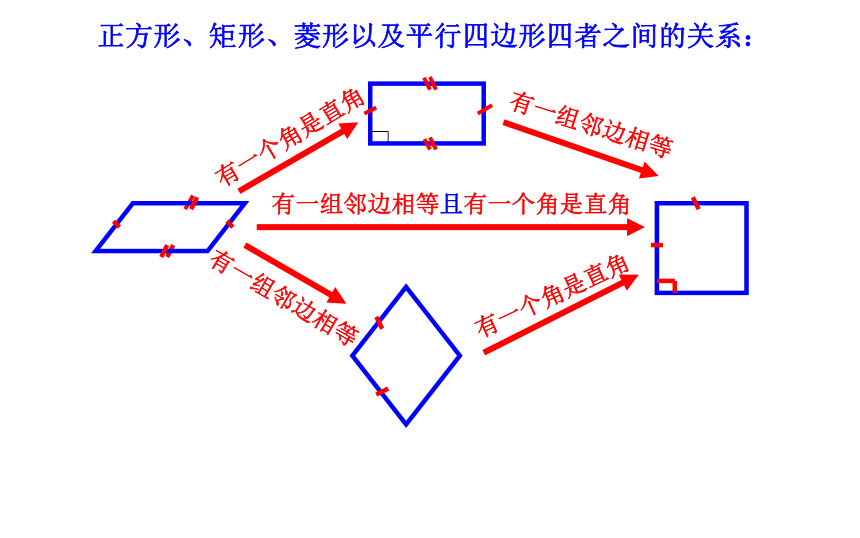
正方形、矩形、菱形以及平行四边形四者之间的关系:
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
平行四边形
矩形
菱形
正
方
形
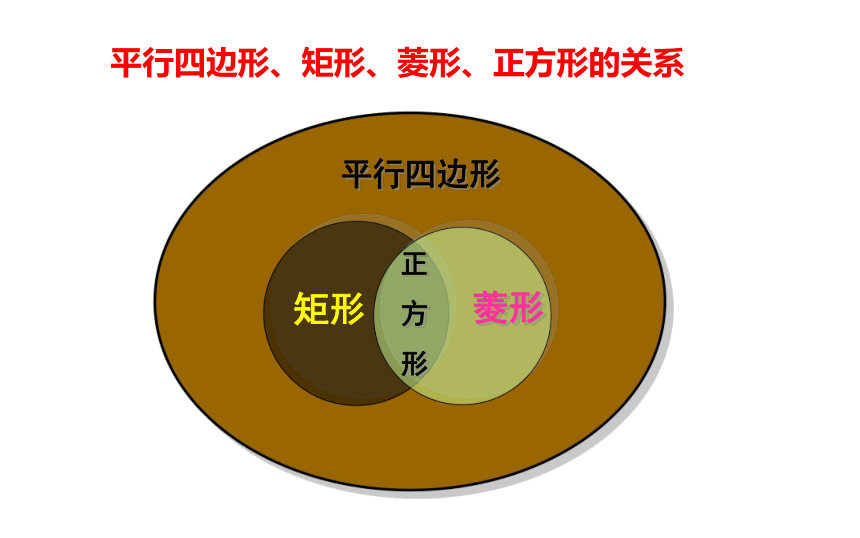
平行四边形、矩形、菱形、正方形的关系
E
A
B
C
D
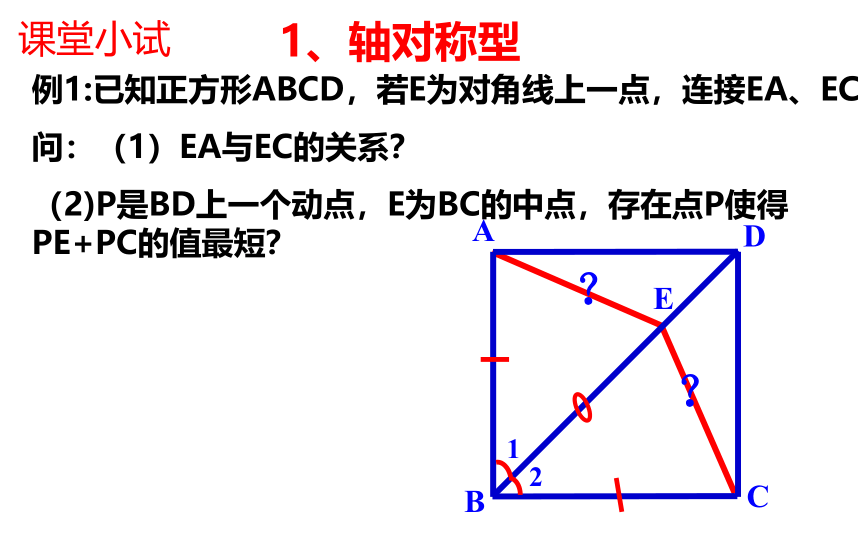
例1:已知正方形ABCD,若E为对角线上一点,连接EA、EC.
问:(1)EA与EC的关系?
(2)P是BD上一个动点,E为BC的中点,存在点P使得PE+PC的值最短?
1
2
?
?
课堂小试
1、轴对称型
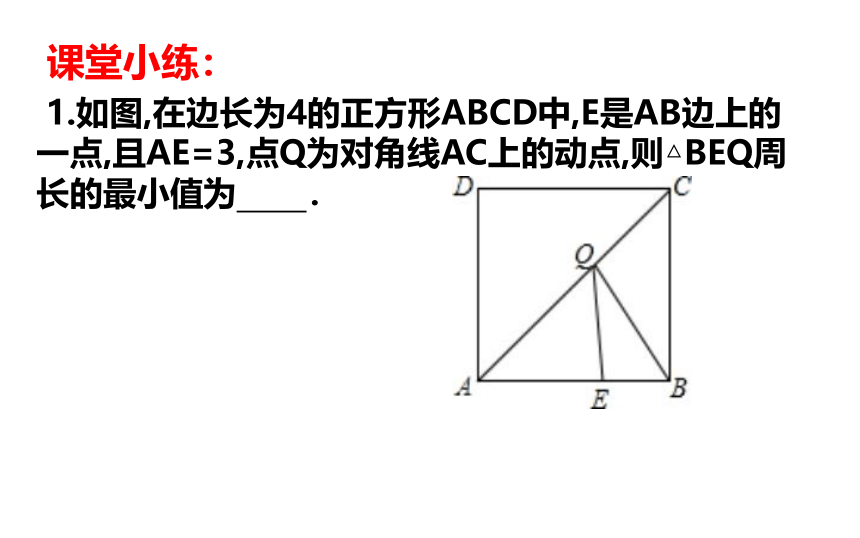
1.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为 .
课堂小练:
能力提升中考链接
1.(2017广东)如图1-23-5,在正方形ABCD中,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是 ( )
A.①③
B.②③
C.①④
D.②④
C
2、手拉手型
例2:正方形ABCD和正方形AEFG,
E
F
A
G
B
C
D
ED和BG的关系?
C
3.正方形中互相垂直的两条线段相等。
(十字架型)
例3:(1)正方形ABCD,E为BC边上一点,AE⊥BF。
A
B
C
D
E
F
G
H
(2)E为AD上任意一点,EF⊥GH
B
A
C
D
E
F
那么AE与BF的关系?
.在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
小小设计师
1. 边长相等的两个正方形ABCD与正方形A′ B ′ C ′ O,点O是正方形ABCD对角线的交点,又是正方形A′ B ′ C ′ O 的一个顶点。当正方形A′ B ′ C ′ O 绕O点旋转时,请回答下列问题:
(1)当B、C 两点分别落在A′ O、C ′ O上时,如图(1),重叠部分的面积与正方形ABCD面积有何数量关系?
知识应用
图(1)
例2 边长相等的两个正方形ABCD与正方形A′ B ′ C ′ O,点O是正方形ABCD对角线的交点,又是正方形A′ B ′ C ′ O 的一个顶点。当正方形A′ B ′ C ′ O 绕O点旋转时,请回答下列问题:
(2)当旋转到如图(2)所示的位置时,重叠部分的面积与正方形ABCD面积有何数量关系?并说明理由.
知识应用
图(2)
3. 如图,正方形ABCD中,点E,F分别在
AD,CD上,且DE=CF,AF与BE相交于点G.
(1)求证:BE=AF;
(2)若AB=4,DE=1,求AG的长.
试试自己的能力有多大吧!
4.半角模型
例4:正方形ABCD,∠FAE=45°,如图所示,有什么结论?
(1)BE+DF=EF
(2)∠AEB=∠AEF=∠ANM=∠DNF;
∠AFD=∠AFE=∠AMN=∠BME;
(3)△ANM∽ △AEF∽ △BEM∽△DNF
(4)AN=NE,AN⊥NE
(5)MN:EF=
小试牛刀
4.如图,正方形ABCD中,点E、 F分别在线段BC、CD上运动,且满足∠EAF=45°,AE、AF分别与BD相交于点M、N,下列说法中:①BE+DF=EF;②点A到线段EF的距离一定等于正方形的边长;③若tan∠BAE=,则tan∠DAF=;④若BE=2,DF=3,则S△AEF=15.其中结论正确是 .
总结
1、正方形的性质。
2、正方形性质的综合应用。
3、轴对称型、手拉手型、十字架型、半角型。
难点:正方形性质和三角形有关知识结合的综合应用
平行四边形
菱 形
定义:有一组邻边相等的平行四边形叫做菱形
平行四边形
一个角是直角
矩 形
定义:有一个角是直角的平行四边形叫做矩形
一组邻边相等
复习导入:
矩 形
正方形
〃
〃
矩形怎样变化后就成了正方形呢?
探 究(一)
知识讲解
探 究(二)
菱形怎样变化后就成了正方形呢?
正方形
正 方 形 的 性 质
边
角
对角线
对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行, 四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD 是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形 中心对称图形
正方形、矩形、菱形以及平行四边形四者之间的关系:
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
平行四边形
矩形
菱形
正
方
形
平行四边形、矩形、菱形、正方形的关系
E
A
B
C
D
例1:已知正方形ABCD,若E为对角线上一点,连接EA、EC.
问:(1)EA与EC的关系?
(2)P是BD上一个动点,E为BC的中点,存在点P使得PE+PC的值最短?
1
2
?
?
课堂小试
1、轴对称型
1.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为 .
课堂小练:
能力提升中考链接
1.(2017广东)如图1-23-5,在正方形ABCD中,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是 ( )
A.①③
B.②③
C.①④
D.②④
C
2、手拉手型
例2:正方形ABCD和正方形AEFG,
E
F
A
G
B
C
D
ED和BG的关系?
C
3.正方形中互相垂直的两条线段相等。
(十字架型)
例3:(1)正方形ABCD,E为BC边上一点,AE⊥BF。
A
B
C
D
E
F
G
H
(2)E为AD上任意一点,EF⊥GH
B
A
C
D
E
F
那么AE与BF的关系?
.在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
小小设计师
1. 边长相等的两个正方形ABCD与正方形A′ B ′ C ′ O,点O是正方形ABCD对角线的交点,又是正方形A′ B ′ C ′ O 的一个顶点。当正方形A′ B ′ C ′ O 绕O点旋转时,请回答下列问题:
(1)当B、C 两点分别落在A′ O、C ′ O上时,如图(1),重叠部分的面积与正方形ABCD面积有何数量关系?
知识应用
图(1)
例2 边长相等的两个正方形ABCD与正方形A′ B ′ C ′ O,点O是正方形ABCD对角线的交点,又是正方形A′ B ′ C ′ O 的一个顶点。当正方形A′ B ′ C ′ O 绕O点旋转时,请回答下列问题:
(2)当旋转到如图(2)所示的位置时,重叠部分的面积与正方形ABCD面积有何数量关系?并说明理由.
知识应用
图(2)
3. 如图,正方形ABCD中,点E,F分别在
AD,CD上,且DE=CF,AF与BE相交于点G.
(1)求证:BE=AF;
(2)若AB=4,DE=1,求AG的长.
试试自己的能力有多大吧!
4.半角模型
例4:正方形ABCD,∠FAE=45°,如图所示,有什么结论?
(1)BE+DF=EF
(2)∠AEB=∠AEF=∠ANM=∠DNF;
∠AFD=∠AFE=∠AMN=∠BME;
(3)△ANM∽ △AEF∽ △BEM∽△DNF
(4)AN=NE,AN⊥NE
(5)MN:EF=
小试牛刀
4.如图,正方形ABCD中,点E、 F分别在线段BC、CD上运动,且满足∠EAF=45°,AE、AF分别与BD相交于点M、N,下列说法中:①BE+DF=EF;②点A到线段EF的距离一定等于正方形的边长;③若tan∠BAE=,则tan∠DAF=;④若BE=2,DF=3,则S△AEF=15.其中结论正确是 .
总结
1、正方形的性质。
2、正方形性质的综合应用。
3、轴对称型、手拉手型、十字架型、半角型。
