八年级数学下册课件-19.1.1 变量与函数58-人教版(共14张ppt)
文档属性
| 名称 | 八年级数学下册课件-19.1.1 变量与函数58-人教版(共14张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-05 00:00:00 | ||
图片预览






文档简介
19.1.1 变量与函数(1)
——变量与常量
第十九章 一次函数 19.1 函数
万物皆变
一、教学目标:
1.知识与技能:了解常量与变量的含义,能分清实例中的常量与变量,学会用含一个变量的代数式表示另一个变量。
2.过程与方法:经历观察、分析、思考等数学活动过程,发展合情推理,以提高分析问题和解决问题的能力
3.情感态度与价值观:引导学生探索实际问题的数量关系,渗透事物是运动的,运动是有规律的辩证思想。
二、教学重点:
认识变量与常量,会用式子表示变量间的关系
三、教学难点:
用含一个变量的式子表示另一个变量
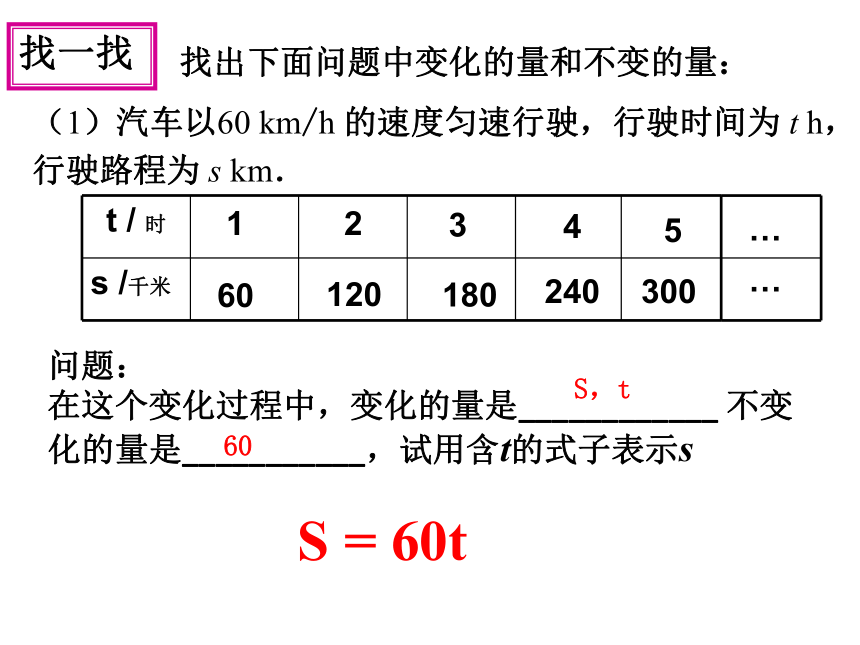
找一找
(1)汽车以60 km/h 的速度匀速行驶,行驶时间为 t h,
行驶路程为 s km.
t / 时
s /千米
1
60
2
120
3
180
4
240
5
300
问题:
在这个变化过程中,变化的量是____________ 不变化的量是___________,试用含t的式子表示s
找出下面问题中变化的量和不变的量:
S,t
60
S = 60t
…
…
(2)每张电影票的售价为10 元,设某场电影售出x 张票,票房收入为y 元.
第一场售出150张票,则第一场电影的票房收入为 __元;?
第二场售出205张票,则第二场电影的票房收入为______元;?
第三场售出310张票,则第三场电影的票房收入为 元.?
……
1500
2050
3100
问题:
在这个变化过程中,变化的量是_______________
不变化的量是___________,试用含x的式子表示y
x ,y
10
y =10 x
(3)圆形水波慢慢地扩大,在这一过程中,当圆的半径r 分别为10 cm,20 cm,30 cm 时,圆的面积S 分别
为多少?在这个过程中,哪些量是变化的?
{2D5ABB26-0587-4C30-8999-92F81FD0307C}半径r(cm)
10
20
30
…
圆面积S(cm2)
…
问题:
在这个变化过程中,变化的量是____________
不变化的量是________,试用含r的式子表示S
r ,S
找一找
x
y
A
B
C
D
(4)用10 m长的绳子围一个矩形,当矩形的一边长x
分别为3 m,3.5 m,4 m,4.5 m 时,它的邻边长y 分
别为多少?在矩形改变形状的变化过程中,哪些量是
变化的?哪些量是固定不变的?
问题:
在这个变化过程中,变化的量是_______________
不变化的量是________,试用含x的式子表示y
x, y
10
y=5- x
说一说
上述运动变化过程中出现的量,你认为可以怎样分类?
在一个变化过程中,数值发生变化的量为变量.
变量:
在一个变化过程中,数值始终不变的量为常量.
常量:
说一说
你能举出一个变化过程的例子,并说出其中的变量
和常量吗?试一试!
练一练
(1)直角三角形中的一个锐角α与另一个锐角β之间的
关系。
写出下列问题中的关系式,指出下列变化过
程中的变量和常量:
(2)用20cm长的铁丝所围成的长方形的长x(单位:cm)与面积s(单位:cm)的关系
(3)一个盛满30t水的水箱,每小时流出0.5t水,试用流水时间t(单位:h),表示水箱中的剩余水量y(单位:t)
(4)甲、乙两地相距y km,一人骑自行车以每小时10 km的速度从甲地向乙地行驶,试用行驶时间t(单位:h)表示该人离乙地的距离s(单位:km)
拓展题
5.观察下列图形的构成规律完成各题
……
第1个
第2个
第4个
第3个
(1)第8个图形中有_____个圆,第10个图形中有____个圆
(2)设第n个图形中圆的个数为w,试写出w与n之间的关系式
(3)所确定的关系式中的常量与变量分别是什么?
2.会用一个变量表示另一个变量
1.变量、常量的概念
变量:在一个变化过程中,数值发生变化的量为变量.
常量:在一个变化过程中,数值始终不变的量为常量.
课堂小结
作业:课本71页练习(1)(2)(3)(4)
——变量与常量
第十九章 一次函数 19.1 函数
万物皆变
一、教学目标:
1.知识与技能:了解常量与变量的含义,能分清实例中的常量与变量,学会用含一个变量的代数式表示另一个变量。
2.过程与方法:经历观察、分析、思考等数学活动过程,发展合情推理,以提高分析问题和解决问题的能力
3.情感态度与价值观:引导学生探索实际问题的数量关系,渗透事物是运动的,运动是有规律的辩证思想。
二、教学重点:
认识变量与常量,会用式子表示变量间的关系
三、教学难点:
用含一个变量的式子表示另一个变量
找一找
(1)汽车以60 km/h 的速度匀速行驶,行驶时间为 t h,
行驶路程为 s km.
t / 时
s /千米
1
60
2
120
3
180
4
240
5
300
问题:
在这个变化过程中,变化的量是____________ 不变化的量是___________,试用含t的式子表示s
找出下面问题中变化的量和不变的量:
S,t
60
S = 60t
…
…
(2)每张电影票的售价为10 元,设某场电影售出x 张票,票房收入为y 元.
第一场售出150张票,则第一场电影的票房收入为 __元;?
第二场售出205张票,则第二场电影的票房收入为______元;?
第三场售出310张票,则第三场电影的票房收入为 元.?
……
1500
2050
3100
问题:
在这个变化过程中,变化的量是_______________
不变化的量是___________,试用含x的式子表示y
x ,y
10
y =10 x
(3)圆形水波慢慢地扩大,在这一过程中,当圆的半径r 分别为10 cm,20 cm,30 cm 时,圆的面积S 分别
为多少?在这个过程中,哪些量是变化的?
{2D5ABB26-0587-4C30-8999-92F81FD0307C}半径r(cm)
10
20
30
…
圆面积S(cm2)
…
问题:
在这个变化过程中,变化的量是____________
不变化的量是________,试用含r的式子表示S
r ,S
找一找
x
y
A
B
C
D
(4)用10 m长的绳子围一个矩形,当矩形的一边长x
分别为3 m,3.5 m,4 m,4.5 m 时,它的邻边长y 分
别为多少?在矩形改变形状的变化过程中,哪些量是
变化的?哪些量是固定不变的?
问题:
在这个变化过程中,变化的量是_______________
不变化的量是________,试用含x的式子表示y
x, y
10
y=5- x
说一说
上述运动变化过程中出现的量,你认为可以怎样分类?
在一个变化过程中,数值发生变化的量为变量.
变量:
在一个变化过程中,数值始终不变的量为常量.
常量:
说一说
你能举出一个变化过程的例子,并说出其中的变量
和常量吗?试一试!
练一练
(1)直角三角形中的一个锐角α与另一个锐角β之间的
关系。
写出下列问题中的关系式,指出下列变化过
程中的变量和常量:
(2)用20cm长的铁丝所围成的长方形的长x(单位:cm)与面积s(单位:cm)的关系
(3)一个盛满30t水的水箱,每小时流出0.5t水,试用流水时间t(单位:h),表示水箱中的剩余水量y(单位:t)
(4)甲、乙两地相距y km,一人骑自行车以每小时10 km的速度从甲地向乙地行驶,试用行驶时间t(单位:h)表示该人离乙地的距离s(单位:km)
拓展题
5.观察下列图形的构成规律完成各题
……
第1个
第2个
第4个
第3个
(1)第8个图形中有_____个圆,第10个图形中有____个圆
(2)设第n个图形中圆的个数为w,试写出w与n之间的关系式
(3)所确定的关系式中的常量与变量分别是什么?
2.会用一个变量表示另一个变量
1.变量、常量的概念
变量:在一个变化过程中,数值发生变化的量为变量.
常量:在一个变化过程中,数值始终不变的量为常量.
课堂小结
作业:课本71页练习(1)(2)(3)(4)
