重庆市南开高级中学2020-2021学年高一上学期期中考试数学试卷 PDF版含答案
文档属性
| 名称 | 重庆市南开高级中学2020-2021学年高一上学期期中考试数学试卷 PDF版含答案 |
|
|
| 格式 | |||
| 文件大小 | 247.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 00:00:00 | ||
图片预览




文档简介
重庆南开中学高 2023 级高一(上)期中考试
数学试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.
第Ⅰ卷(选择题 共 60 分)
一、选择题:本大题8 个小题,每小题 5 分,共 40 分,每小题只.有.一.个.选项符
合要求,答案请涂写在机读卡上.
1. 已知集合A??x x?3?,B ???1,0,1,2,3,4,5?,则?CRA??B ?
A. {?1,0,1,2} B. {?1,0,1} C. {3,4,5} D. {x|x?3}
2. “?x?1,x?0.”的否定是
A. ?x ?1,x?0 B. ?x?1,x?0 C. ?x?1,x?0 D. ?x?1,x?0
3. 下列函数是偶函数且在?0,???上单调递增的是
2 2 3
A. y ? ?x B. y ? x ?2x C. y ? x D. y ? x
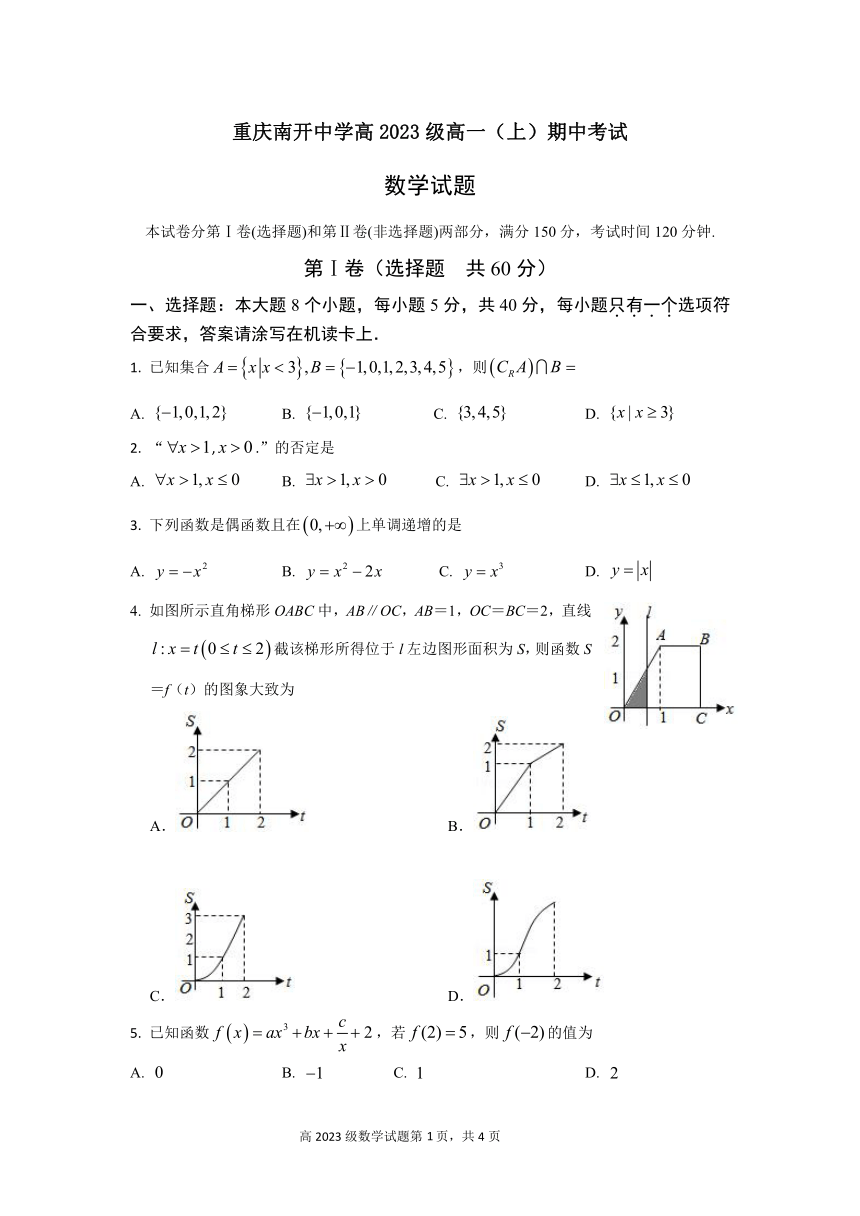
4. 如图所示直角梯形OABC中,AB∥OC,AB=1,OC=BC=2,直线
l:x ?t?0?t ?2?截该梯形所得位于l左边图形面积为S,则函数S
=f(t)的图象大致为
A. B.
C. D.
c
5. 已知函数 3
f ?x??ax ?bx? ?2,若 f(2)?5,则 f(?2)的值为
x
A. 0 B. ?1 C. 1 D. 2
高2023级数学试题第1页,共4页
6. 函数 f ?x?? x?2 x?1的值域为
A. R B. [1,??) C. [0,??) D. (?2,??)
7.已知 y ? f ?x?是定义在R上的偶函数,f(3)?0,且 f(x)在x?[0,??)单调递增,则
不等式(x?2)f(x)?0的解为
A.???,?1??(3,??) B.??2,?1??(2,??)
C.??3,0??(3,??) D.??3,?2??(3,??)
8. 已知x,y ?0,且xy?2x? y ?7,则x? y的最小值为
A. 3 B. 1 C. 4 D. 2
二、多选题:本题共 4 小题,每小题 5 分,共 20 分。在每小题给出的选项中,
有多项符合题目要求。全部选对的得 5 分,有选错的得 0 分,部分选对的得 3
分。
2
9. “?x??1,2?,x ?x?a?0”的充分不必要条件是
A. a????,7? B. a????,5? C. a????,4? D. a??6,???
10. 下列说法正确的是
2 2 1
A. 若a ?b,则ac ?bc B. 存在a,使得不等式a? ?2成立
a
b?m b
C. 若a ?b?0,m?0,则 ? D. 若a?b?c,且a?b?c?0 则ac?bc
a?m a
2
??x ?(2a?4)x x??1
?
11. 已知函数 f ?x???x?a 在R上单调递增,则a可以是
? x??1
?x?2
A. ?1 B. 0 C. 1 D. 3
x?a
12. 已知函数 f ?x?? 2 ,则以下说法正确的有
x ?bx?1
A.若 f ?x?为奇函数,则a?b?0
B.对任意a,b?R, f ?x?不可能是偶函数
C. 当a?b?1时,函数在?0,???上单调递增
D.若不存在M ,使得 f ?x? ? M 恒成立,则b?(??,?2]?[2,??)
高2023级数学试题第2页,共4页
第Ⅱ卷(非选择题 共 90 分)
三、填空题:本大题 4 个小题,每小题 5 分,共 20 分. 各题答案必须填写在答
题卡上相应位置(只填结果,不写过程).
x?2
13.已知函数 f ?x?1?? ,则 f(3)?_____________
x
1
14.已知 f(x) 是定义在 R 上的奇函数,且 2
x ?0 时, f(x)? x ? ,则 x?0 时,
x
f(x)?_____________
x?2
15. 函数 y ? 的单调递减区间为_______________
x?1
?x?1
16. 已知函数 2
f ?x?? ,g?x?? x ?ax ,若对任意x1???1,0?,都存在x2??1,3?,
x?2
使得 f ?x1?? g?x2?,则a的范围是______________
四、解答题:本大题 6 个小题,共 70 分. 各题解答必须答在答题卡上(必须写
出必要的文字说明、演算步骤或推理过程).
17.已知函数 2
f ?x?? x ?ax?3?a 。
(1)若a ?3,求 f ?x?的定义域和单调区间;
(2)若 f ?x?定义域为R,求a的取值范围。
2x?1
18.已知集合A?{x ?1},B ?{x|x?a|?3}。
x?2
(1)若a ?3,求A?B;
(2)若x?A是x?B的充分不必要条件,求a的范围。
2
19.已知二次函数 f ?x??ax ?bx?c,满足 f ?x?1?? f ?x??2x?3,且 f ?x?在R上的
最小值为?1。
(1)求 f ?x?的解析式;
f ?x??k
(2)令g?x?? ,若g?x?在[1,??)上单调递增,求k的取值范围。
x
高2023级数学试题第3页,共4页
20.已知定义在?0,???上的函数 f ?x?对任意x,y均满足 f ?xy??2020? f ?x?? f ?y?,
若对任意x?1, f ?x??2020。
(1)求 f ?1?并判断函数 f ?x?的单调性并证明;
(2)解不等式 f ?x?? f ?x?1?? 4040。
2
?x ?10x?100,0? x?20
?
21. 某工厂生产某种产品,每年生产x万件,总成本为 f(x)?? 3600 (万
?35x? ?180,x?20
? x
元),每件商品售价为34元.通过市场分析,该厂生产的商品能全部售完。
f(x)
(1)求每件产品的成本g(x)? (元/件)的最小值;
x
(2)写出年利润L(x)(万元)关于年产量x(万件)的函数解析式,并求出
年产量为多少万件时,该厂在这一商品的生产中所获利润最大?
2
22.已知函数 2
f ?x???x?1? ?a ,g?x?? 2x x?a ?5 。
(1)若g?x?在?1,2?上单调递增,求a的范围;
(2)若对任意的x???1,1?,都有 f ?x?? g?x?恒成立,求a的取值范围。
高2023级数学试题第4页,共4页
重庆南开中学高 2023 级高一(上)期中考试
数学参考答案
一、选择题
CCDC BCDA
二、多选题
9.AC 10.BCD 11.ABC 12.ABD
三、填空题
2 1 ?1 7?
13.2 14.?x ? 15. ?1,2? 16.? , ?
x ?2 3?
四、解答题
17. (1) 2
f ?x?? x ?3x ,定义域为(??,0]?[3,??)。
(2) f ?x?定义域为R,即 2
x ?ax?3?a?0在R上恒成立,
即 2
??a ?4?3?a??0,解得?6?a?2 。
18. (1)当a ?3时,A?[?1,2),B ??0,6?,A?B?[0,2)
? a?3?2
(2)由x?A是x?B的充分不必要条件,可得A是B的真子集,? ,
?a?3??1
解得?1?a?2。经检验,发现a ??1和a ?2均满足题意,故?1?a?2。
? 2a?2
19. (1) f ?x?1?? f ?x??2a?a?b?2x?3 ,得? ,解得a?1,b?2。此时
?a?b?3
2
f ?x?? x ?2x?c ,当x??1时,函数取得最小值?1,可得c ?0,故 2
f ?x?? x ?2x。
k k k
(2)g?x?? x? ?2,令u ? x? ?2,g?x?在[1,??)上单调递增,即u ? x? ?2
x x x
高2023级数学试题第5页,共4页
k
在[1,??)上单调递增,且u ? x? ?2?0在[1,??)上恒成立。
x
k 2
u ? x? ?2?0在[1,??)上恒成立,可得k ??x ?2x在[1,??)上恒成立,即k ??3
x
k
当k ?0时,u ? x? ?2在[1,??)上单调递增,满足题意
x
当k ?0时,u ? x?2在[1,??)上单调递增,满足题意
k
当k ?0时,要使u ? x? ?2在[1,??)上单调递增,只需 k ?1,即0?k ?1。
x
综上,k 的取值范围是??3,1?
20.(1)任取x1,x2 ?0,设x2 ?tx1,?t ?1?,则x2 ? x1, f ?t??2020
由题意得 f ?x2?? f ?tx1?? f ?x1?? f ?t?? 2020? f ?x1 ?
故 f ?x?在?0,???上单调递减。
(2)令x? y?1可得 f ?1??2020
由 f ?x?? f ?x?1?? 4040,可得 f ?x?? f ?x?1??2020? 2020? f ?1?
即 f ?x?x?1??? f ?1?,由 f ?x?在?0,???上单调递减,
?x?x?1??1
? ?1? 5
可得? x?0 解得0? x?
? 2
? x?1?0
? 100
( ) ??x?10? ,0? x?20
f x
21. (1) x
g(x)? ?? ,
x ? 3600 180
35? 2 ? ,x?20
?? x x
100 100
当0? x?20,g(x)? x?10? ?10?2 x? ?30,当x?10取最小值30。
x x
3600 180 1 1
当x?20,g(x)?35? 2 ? ,令t ? ?(0, ) ,
x x x 20
2 1 3
y ?35?3600t ?180t,当t ? ,即x?40,取最小值32
40 4
综上所述,当x?10取最小值30。
高2023级数学试题第6页,共4页
2
??x ?24x?100,0? x?20
?
L(x)?34x? f(x)?? 3600
??x? ?180,x?20
? x
2 2
0? x?20时,?x ?24x?100??(x?12) ?44?44,当x?12,最大值为44
3600 3600 3600
x?20时,?x? ?180?180-(x? )?180-2 x? ?60,
x x x
当x?60,取最大值60。
综上所述,当x?60,取最大值60。
2
? 2x ?2ax?5 x?a
22(1)g?x??? 2
??2x ?2ax?5 x?a
?a ?
①当a?0时,g?x?在? ,???上单调递增,满足条件
?2 ?
? a? a
②当a ?0时,g?x?在???, ?,?a,???上单调递增,故 ?2或a?1。
? 2? 2
故当a?1或a?4时,若g?x?在?1,2?上单调递增。
2
(2)由于对任意的 2
x???1,1?,都有 f ?x?? g?x?恒成立,可得2x x?a ??x?1? ?a ?5
在x???1,1?上恒成立。
即 2 2 2 2 2 2
2x ?2ax? x ?2x?a ?4或者2x ?2ax??x ?2x?a ?4恒成立。
对于 2 2 2 2 2
2x ?2ax??x ?2x?a ?4,化简得3x ?2?a?1?x?a ?4?0,
2
此时 2 2
?1?4?a?1? ?12?a ?4???2a ?4a?8?0 恒成立,
即 2 2
3x ?2?a?1?x?a ?4?0恒不成立。
故只有 2 2 2 2 2
2x ?2ax??x ?2x?a ?4,即x ?2?a?1?x?a ?4?0在x???1,1?上恒成
立。令 2 2
h?x?? x ?2?a?1?x?a ?4。
2 ?1? 7 ?1? 7
①当 2
??4?a?1? ?4?4?a ??0 即 ?a? 时,
2 2
高2023级数学试题第7页,共4页
2 2
x ?2?a?1?x?a ?4?0在R上恒成立,满足题意
②当 2 2
h?x??0的两根均小于?1时,x ?2?a?1?x?a ?4?0在x???1,1?上恒成立。
? ??0
?
此时?a?1??1,解得a??
??h??1??0
③当 2 2
h?x??0的两根均大于1时,x ?2?a?1?x?a ?4?0在x???1,1?上恒成立。
? ??0
?
此时?a?1?1,解得0?a?1
??h?1??0
??1? 7 ?
综上,a??? ,1?
? 2 ??
高2023级数学试题第8页,共4页
数学试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.
第Ⅰ卷(选择题 共 60 分)
一、选择题:本大题8 个小题,每小题 5 分,共 40 分,每小题只.有.一.个.选项符
合要求,答案请涂写在机读卡上.
1. 已知集合A??x x?3?,B ???1,0,1,2,3,4,5?,则?CRA??B ?
A. {?1,0,1,2} B. {?1,0,1} C. {3,4,5} D. {x|x?3}
2. “?x?1,x?0.”的否定是
A. ?x ?1,x?0 B. ?x?1,x?0 C. ?x?1,x?0 D. ?x?1,x?0
3. 下列函数是偶函数且在?0,???上单调递增的是
2 2 3
A. y ? ?x B. y ? x ?2x C. y ? x D. y ? x
4. 如图所示直角梯形OABC中,AB∥OC,AB=1,OC=BC=2,直线
l:x ?t?0?t ?2?截该梯形所得位于l左边图形面积为S,则函数S
=f(t)的图象大致为
A. B.
C. D.
c
5. 已知函数 3
f ?x??ax ?bx? ?2,若 f(2)?5,则 f(?2)的值为
x
A. 0 B. ?1 C. 1 D. 2
高2023级数学试题第1页,共4页
6. 函数 f ?x?? x?2 x?1的值域为
A. R B. [1,??) C. [0,??) D. (?2,??)
7.已知 y ? f ?x?是定义在R上的偶函数,f(3)?0,且 f(x)在x?[0,??)单调递增,则
不等式(x?2)f(x)?0的解为
A.???,?1??(3,??) B.??2,?1??(2,??)
C.??3,0??(3,??) D.??3,?2??(3,??)
8. 已知x,y ?0,且xy?2x? y ?7,则x? y的最小值为
A. 3 B. 1 C. 4 D. 2
二、多选题:本题共 4 小题,每小题 5 分,共 20 分。在每小题给出的选项中,
有多项符合题目要求。全部选对的得 5 分,有选错的得 0 分,部分选对的得 3
分。
2
9. “?x??1,2?,x ?x?a?0”的充分不必要条件是
A. a????,7? B. a????,5? C. a????,4? D. a??6,???
10. 下列说法正确的是
2 2 1
A. 若a ?b,则ac ?bc B. 存在a,使得不等式a? ?2成立
a
b?m b
C. 若a ?b?0,m?0,则 ? D. 若a?b?c,且a?b?c?0 则ac?bc
a?m a
2
??x ?(2a?4)x x??1
?
11. 已知函数 f ?x???x?a 在R上单调递增,则a可以是
? x??1
?x?2
A. ?1 B. 0 C. 1 D. 3
x?a
12. 已知函数 f ?x?? 2 ,则以下说法正确的有
x ?bx?1
A.若 f ?x?为奇函数,则a?b?0
B.对任意a,b?R, f ?x?不可能是偶函数
C. 当a?b?1时,函数在?0,???上单调递增
D.若不存在M ,使得 f ?x? ? M 恒成立,则b?(??,?2]?[2,??)
高2023级数学试题第2页,共4页
第Ⅱ卷(非选择题 共 90 分)
三、填空题:本大题 4 个小题,每小题 5 分,共 20 分. 各题答案必须填写在答
题卡上相应位置(只填结果,不写过程).
x?2
13.已知函数 f ?x?1?? ,则 f(3)?_____________
x
1
14.已知 f(x) 是定义在 R 上的奇函数,且 2
x ?0 时, f(x)? x ? ,则 x?0 时,
x
f(x)?_____________
x?2
15. 函数 y ? 的单调递减区间为_______________
x?1
?x?1
16. 已知函数 2
f ?x?? ,g?x?? x ?ax ,若对任意x1???1,0?,都存在x2??1,3?,
x?2
使得 f ?x1?? g?x2?,则a的范围是______________
四、解答题:本大题 6 个小题,共 70 分. 各题解答必须答在答题卡上(必须写
出必要的文字说明、演算步骤或推理过程).
17.已知函数 2
f ?x?? x ?ax?3?a 。
(1)若a ?3,求 f ?x?的定义域和单调区间;
(2)若 f ?x?定义域为R,求a的取值范围。
2x?1
18.已知集合A?{x ?1},B ?{x|x?a|?3}。
x?2
(1)若a ?3,求A?B;
(2)若x?A是x?B的充分不必要条件,求a的范围。
2
19.已知二次函数 f ?x??ax ?bx?c,满足 f ?x?1?? f ?x??2x?3,且 f ?x?在R上的
最小值为?1。
(1)求 f ?x?的解析式;
f ?x??k
(2)令g?x?? ,若g?x?在[1,??)上单调递增,求k的取值范围。
x
高2023级数学试题第3页,共4页
20.已知定义在?0,???上的函数 f ?x?对任意x,y均满足 f ?xy??2020? f ?x?? f ?y?,
若对任意x?1, f ?x??2020。
(1)求 f ?1?并判断函数 f ?x?的单调性并证明;
(2)解不等式 f ?x?? f ?x?1?? 4040。
2
?x ?10x?100,0? x?20
?
21. 某工厂生产某种产品,每年生产x万件,总成本为 f(x)?? 3600 (万
?35x? ?180,x?20
? x
元),每件商品售价为34元.通过市场分析,该厂生产的商品能全部售完。
f(x)
(1)求每件产品的成本g(x)? (元/件)的最小值;
x
(2)写出年利润L(x)(万元)关于年产量x(万件)的函数解析式,并求出
年产量为多少万件时,该厂在这一商品的生产中所获利润最大?
2
22.已知函数 2
f ?x???x?1? ?a ,g?x?? 2x x?a ?5 。
(1)若g?x?在?1,2?上单调递增,求a的范围;
(2)若对任意的x???1,1?,都有 f ?x?? g?x?恒成立,求a的取值范围。
高2023级数学试题第4页,共4页
重庆南开中学高 2023 级高一(上)期中考试
数学参考答案
一、选择题
CCDC BCDA
二、多选题
9.AC 10.BCD 11.ABC 12.ABD
三、填空题
2 1 ?1 7?
13.2 14.?x ? 15. ?1,2? 16.? , ?
x ?2 3?
四、解答题
17. (1) 2
f ?x?? x ?3x ,定义域为(??,0]?[3,??)。
(2) f ?x?定义域为R,即 2
x ?ax?3?a?0在R上恒成立,
即 2
??a ?4?3?a??0,解得?6?a?2 。
18. (1)当a ?3时,A?[?1,2),B ??0,6?,A?B?[0,2)
? a?3?2
(2)由x?A是x?B的充分不必要条件,可得A是B的真子集,? ,
?a?3??1
解得?1?a?2。经检验,发现a ??1和a ?2均满足题意,故?1?a?2。
? 2a?2
19. (1) f ?x?1?? f ?x??2a?a?b?2x?3 ,得? ,解得a?1,b?2。此时
?a?b?3
2
f ?x?? x ?2x?c ,当x??1时,函数取得最小值?1,可得c ?0,故 2
f ?x?? x ?2x。
k k k
(2)g?x?? x? ?2,令u ? x? ?2,g?x?在[1,??)上单调递增,即u ? x? ?2
x x x
高2023级数学试题第5页,共4页
k
在[1,??)上单调递增,且u ? x? ?2?0在[1,??)上恒成立。
x
k 2
u ? x? ?2?0在[1,??)上恒成立,可得k ??x ?2x在[1,??)上恒成立,即k ??3
x
k
当k ?0时,u ? x? ?2在[1,??)上单调递增,满足题意
x
当k ?0时,u ? x?2在[1,??)上单调递增,满足题意
k
当k ?0时,要使u ? x? ?2在[1,??)上单调递增,只需 k ?1,即0?k ?1。
x
综上,k 的取值范围是??3,1?
20.(1)任取x1,x2 ?0,设x2 ?tx1,?t ?1?,则x2 ? x1, f ?t??2020
由题意得 f ?x2?? f ?tx1?? f ?x1?? f ?t?? 2020? f ?x1 ?
故 f ?x?在?0,???上单调递减。
(2)令x? y?1可得 f ?1??2020
由 f ?x?? f ?x?1?? 4040,可得 f ?x?? f ?x?1??2020? 2020? f ?1?
即 f ?x?x?1??? f ?1?,由 f ?x?在?0,???上单调递减,
?x?x?1??1
? ?1? 5
可得? x?0 解得0? x?
? 2
? x?1?0
? 100
( ) ??x?10? ,0? x?20
f x
21. (1) x
g(x)? ?? ,
x ? 3600 180
35? 2 ? ,x?20
?? x x
100 100
当0? x?20,g(x)? x?10? ?10?2 x? ?30,当x?10取最小值30。
x x
3600 180 1 1
当x?20,g(x)?35? 2 ? ,令t ? ?(0, ) ,
x x x 20
2 1 3
y ?35?3600t ?180t,当t ? ,即x?40,取最小值32
40 4
综上所述,当x?10取最小值30。
高2023级数学试题第6页,共4页
2
??x ?24x?100,0? x?20
?
L(x)?34x? f(x)?? 3600
??x? ?180,x?20
? x
2 2
0? x?20时,?x ?24x?100??(x?12) ?44?44,当x?12,最大值为44
3600 3600 3600
x?20时,?x? ?180?180-(x? )?180-2 x? ?60,
x x x
当x?60,取最大值60。
综上所述,当x?60,取最大值60。
2
? 2x ?2ax?5 x?a
22(1)g?x??? 2
??2x ?2ax?5 x?a
?a ?
①当a?0时,g?x?在? ,???上单调递增,满足条件
?2 ?
? a? a
②当a ?0时,g?x?在???, ?,?a,???上单调递增,故 ?2或a?1。
? 2? 2
故当a?1或a?4时,若g?x?在?1,2?上单调递增。
2
(2)由于对任意的 2
x???1,1?,都有 f ?x?? g?x?恒成立,可得2x x?a ??x?1? ?a ?5
在x???1,1?上恒成立。
即 2 2 2 2 2 2
2x ?2ax? x ?2x?a ?4或者2x ?2ax??x ?2x?a ?4恒成立。
对于 2 2 2 2 2
2x ?2ax??x ?2x?a ?4,化简得3x ?2?a?1?x?a ?4?0,
2
此时 2 2
?1?4?a?1? ?12?a ?4???2a ?4a?8?0 恒成立,
即 2 2
3x ?2?a?1?x?a ?4?0恒不成立。
故只有 2 2 2 2 2
2x ?2ax??x ?2x?a ?4,即x ?2?a?1?x?a ?4?0在x???1,1?上恒成
立。令 2 2
h?x?? x ?2?a?1?x?a ?4。
2 ?1? 7 ?1? 7
①当 2
??4?a?1? ?4?4?a ??0 即 ?a? 时,
2 2
高2023级数学试题第7页,共4页
2 2
x ?2?a?1?x?a ?4?0在R上恒成立,满足题意
②当 2 2
h?x??0的两根均小于?1时,x ?2?a?1?x?a ?4?0在x???1,1?上恒成立。
? ??0
?
此时?a?1??1,解得a??
??h??1??0
③当 2 2
h?x??0的两根均大于1时,x ?2?a?1?x?a ?4?0在x???1,1?上恒成立。
? ??0
?
此时?a?1?1,解得0?a?1
??h?1??0
??1? 7 ?
综上,a??? ,1?
? 2 ??
高2023级数学试题第8页,共4页
同课章节目录
