4.2.2 图形的旋转同步练习(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第四章 图形的平移与旋转
2 图形的旋转
第2课时
考点突破
考点1 旋转作图
例1 画出△ABC绕点O顺时针旋转120°后得到的△A'B'C'。
思路导引: 点A与点A′是对应点,点O为旋转中心,根据旋转角为120°,且按顺时针方向旋转可确定旋转后的各点的对应点,顺次连接各个对应点即可,
方法归纳
旋转作图的一般方法:
(1)找到旋转中心、旋转方向和旋转角度。
(2)找到已知图形的各关键点,作各关键点的对应点。
(3)连接各对应点,即得所求作的图形。
题组训练
1.下图右侧的四个三角形中,不能由△ABC经过旋转得到的是( )
2.如图所示,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是( )
点A B. 点B C. 点C D. 点D
3.如图,在正方形网格中,以点A为旋转中心,将△ABC按逆时针方向旋转90°,画出旋转后的△A1B1C1.
4.将下面的图案绕点O按顺时针方向旋转90°,请作出旋转后的图形。
考点2 旋转的应用
例2 如图,已知△ACB与△DFE是两个全等的直角三角形,量得它们的斜边长为10 cm,较小锐角为30°,将这两个三角形摆成如图①的形状,使点B,C,F,D在同一条直线上,且点C与点F重合,将图①中的△ACB绕点C顺时针方向旋转到图②的位置,点E在AB边上,AC交DE于点G,求线段FG的长.(保留根号)
思路导引: 根据图形旋转的特征,找出对应线段相等、对应角相等是解决问题的关键。
方法归纳
要灵活运用旋转的性质,对应点到旋转中心的距离相等;任一组对应点与旋转中心的连线所成的角相等;同时注意找出图中隐含的等量关系,综合运用相关知识解决问题.
题组训练
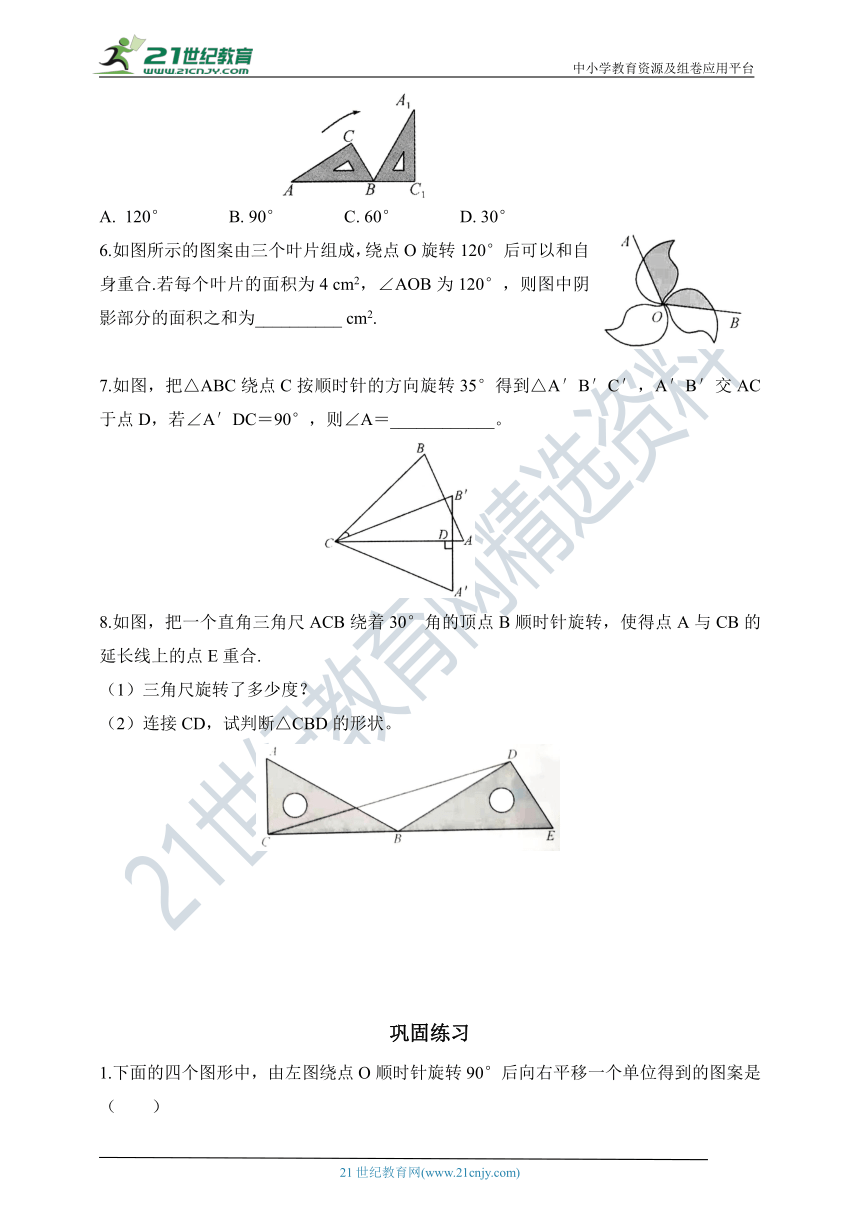
5.如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕点B按顺时针方向转动一个角度到A1BC1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( )
120° B. 90° C. 60° D. 30°
6.如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合.若每个叶片的面积为4 cm2,∠AOB为120°,则图中阴影部分的面积之和为__________ cm2.
7.如图,把△ABC绕点C按顺时针的方向旋转35°得到△A′B′C′,A′B′交AC于点D,若∠A′DC=90°,则∠A=____________。
8.如图,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.
(1)三角尺旋转了多少度?
(2)连接CD,试判断△CBD的形状。
巩固练习
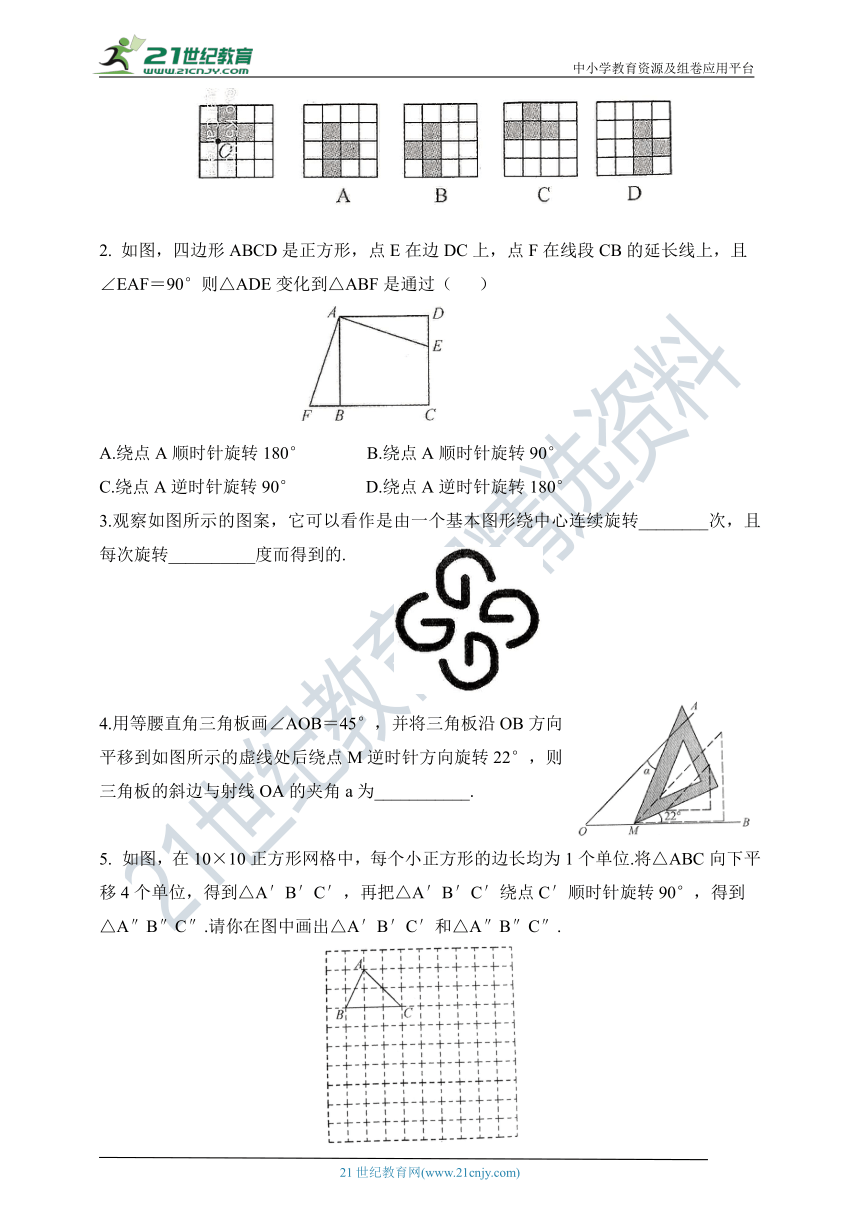
1.下面的四个图形中,由左图绕点O顺时针旋转90°后向右平移一个单位得到的图案是( )
如图,四边形ABCD是正方形,点E在边DC上,点F在线段CB的延长线上,且
∠EAF=90°则△ADE变化到△ABF是通过( )
A.绕点A顺时针旋转180° B.绕点A顺时针旋转90°
C.绕点A逆时针旋转90° D.绕点A逆时针旋转180°
3.观察如图所示的图案,它可以看作是由一个基本图形绕中心连续旋转________次,且每次旋转__________度而得到的.
4.用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°,则三角板的斜边与射线OA的夹角a为___________.
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′顺时针旋转90°,得到
△A″B″C″.请你在图中画出△A′B′C′和△A″B″C″.
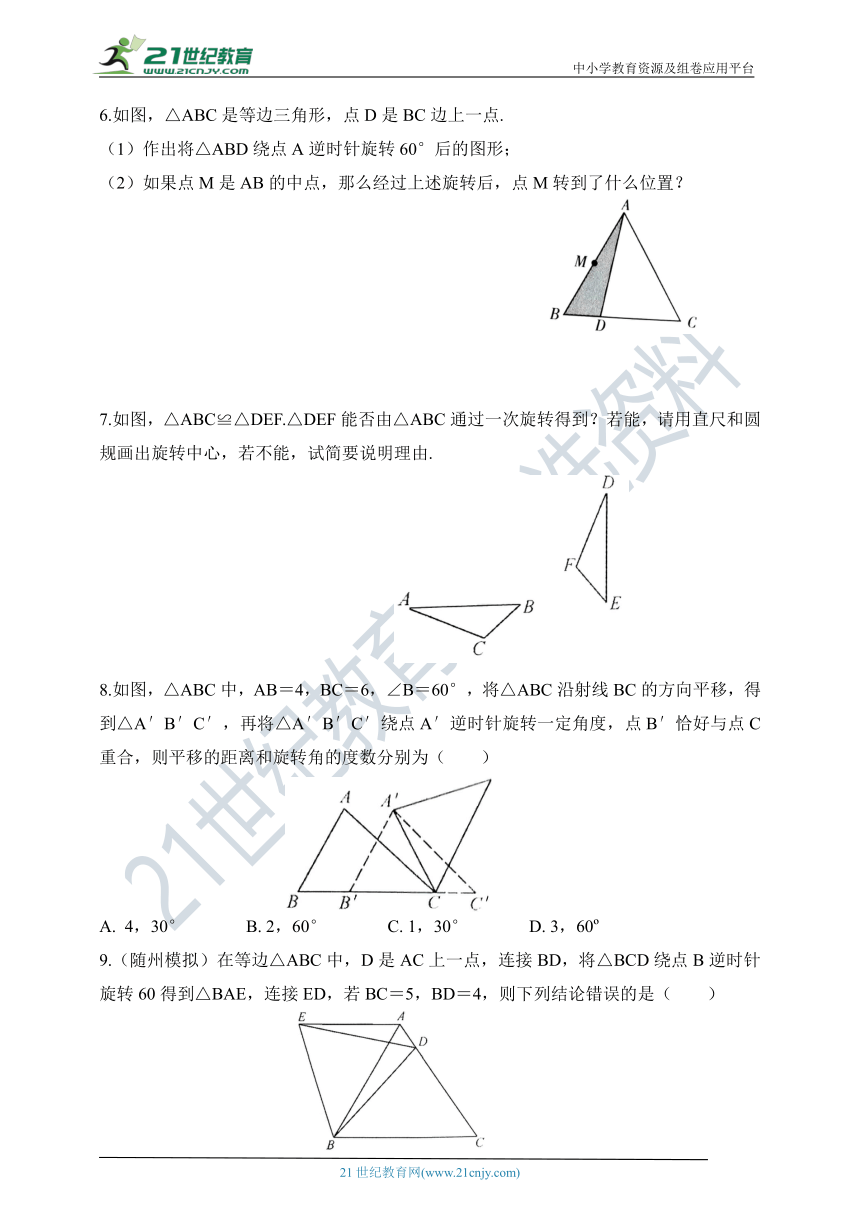
6.如图,△ABC是等边三角形,点D是BC边上一点.
(1)作出将△ABD绕点A逆时针旋转60°后的图形;
(2)如果点M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
7.如图,△ABC≌△DEF.△DEF能否由△ABC通过一次旋转得到?若能,请用直尺和圆规画出旋转中心,若不能,试简要说明理由.
8.如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )
4,30° B. 2,60° C. 1,30° D. 3,60?
9.(随州模拟)在等边△ABC中,D是AC上一点,连接BD,将△BCD绕点B逆时针旋转60得到△BAE,连接ED,若BC=5,BD=4,则下列结论错误的是( )
AE∥BC B. ∠ADE=∠BDC
C. △BDE是等边三角形 D. △ADE的周长是9
10.如图,小明将△ABC绕点O旋转得到△A′B′C′,其中点A′,B′,C′分别是A,B,C的对应点.随即又将△ABC的边AC,BC及旋转中心O及△ABC的位置找到,你认为可以吗?若可以,试确定旋转中心O及△ABC的位置;若不可以,请说明理由.
11.(1)如图1,在正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连接EF,AG.求证:EF=FG.
(2)如图2,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°若BM=1,CN=3,求MN的长.
温馨提示:解答第(2)题时,回忆一下第(1)题的解答方法.
参考答案
考点突破
例1 解:(1)连接OA,OB,OC;(2)分别以OA,OB,OC为一边作∠AOA′=∠BOB′=∠COC′=120°;(3)分别在射线OA′,OB′,OC′上截取OA′=OA,OB′=OB,OC′=OC;(4)连接A′B′,B′C′,C′A′,则△A′B′C′就是△ABC绕点O顺时针旋转120°后的图形。
题组训练
B 2. B
3.解:如图所示:
4.解:如图所示:
例2 解:∵BC=EF,∠B=60°,∴△BCE是等边三角形。
∴∠AFE=30°,∴∠GFD=60°。又∵∠D=∠A=30°,∴∠FGD=90°。
在Rt△DEF中,DE=AB=10 cm,∴EF=BC=AB=5 cm.
∴DF=(cm).∴FG=FD=(cm).
题组训练
5. A 6. 4 7. 55?
8. 解:(1)150?;(2)由CB = BD,可知△CBD是等腰三角形。
巩固练习
D 2. B
3. 3 90 4. 22?
5.解:如图所示:
解:(1)如图,△ACE即为所作图形。
点M转到了AC的中点位置上。
解:能,如下图,点O1就是所求作的旋转中心。
B 9. B
10,解:如图,连接AA', BB',分别作AA', BB'的中垂线相交于点O,则点O即为旋转中心,再作C′的对应点C,连接AC, BC,则△ABC的位置也就确定出来了.
解:(1)证明:∵四边形ABCD是正方形,
∴AB=AD, ∠B=∠ADF=∠ADG=∠BAD=90?.
又∵DG=BE,∴△ABE≌△ADG.∴AE=AG,∠BAE=∠DAG.
∵∠BAD=90?, ∠EAF=45?,∴∠BAE+∠FAD=45?。
∴∠DAG+∠FAD=45?,即∠FAG=∠FAE=45?.
又∵AF=AF,∴△AFE≌△AFG. ∴EF=FG.
(2)如图,将△ABM绕点A逆时针旋转90?,得到△ACD,则CD=BM=1,AM=AD,∠B=∠ACB=∠ACD=45?.连接ND,则∠NCD=90°.∵∠BAC=90°,∠MAN=45?,
∴∠BAM+∠CAN=45?,∴∠DAC+∠CAN=45?,即∠NAM=∠NAD=45?.
又∵AN=AN,∴△ANM≌△AND. ∴MN=ND.
在Rt△CDN中,由勾股定理,得ND=,∴MN=.
_21?????????è?????(www.21cnjy.com)_
第四章 图形的平移与旋转
2 图形的旋转
第2课时
考点突破
考点1 旋转作图
例1 画出△ABC绕点O顺时针旋转120°后得到的△A'B'C'。
思路导引: 点A与点A′是对应点,点O为旋转中心,根据旋转角为120°,且按顺时针方向旋转可确定旋转后的各点的对应点,顺次连接各个对应点即可,
方法归纳
旋转作图的一般方法:
(1)找到旋转中心、旋转方向和旋转角度。
(2)找到已知图形的各关键点,作各关键点的对应点。
(3)连接各对应点,即得所求作的图形。
题组训练
1.下图右侧的四个三角形中,不能由△ABC经过旋转得到的是( )
2.如图所示,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是( )
点A B. 点B C. 点C D. 点D
3.如图,在正方形网格中,以点A为旋转中心,将△ABC按逆时针方向旋转90°,画出旋转后的△A1B1C1.
4.将下面的图案绕点O按顺时针方向旋转90°,请作出旋转后的图形。
考点2 旋转的应用
例2 如图,已知△ACB与△DFE是两个全等的直角三角形,量得它们的斜边长为10 cm,较小锐角为30°,将这两个三角形摆成如图①的形状,使点B,C,F,D在同一条直线上,且点C与点F重合,将图①中的△ACB绕点C顺时针方向旋转到图②的位置,点E在AB边上,AC交DE于点G,求线段FG的长.(保留根号)
思路导引: 根据图形旋转的特征,找出对应线段相等、对应角相等是解决问题的关键。
方法归纳
要灵活运用旋转的性质,对应点到旋转中心的距离相等;任一组对应点与旋转中心的连线所成的角相等;同时注意找出图中隐含的等量关系,综合运用相关知识解决问题.
题组训练
5.如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕点B按顺时针方向转动一个角度到A1BC1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( )
120° B. 90° C. 60° D. 30°
6.如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合.若每个叶片的面积为4 cm2,∠AOB为120°,则图中阴影部分的面积之和为__________ cm2.
7.如图,把△ABC绕点C按顺时针的方向旋转35°得到△A′B′C′,A′B′交AC于点D,若∠A′DC=90°,则∠A=____________。
8.如图,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.
(1)三角尺旋转了多少度?
(2)连接CD,试判断△CBD的形状。
巩固练习
1.下面的四个图形中,由左图绕点O顺时针旋转90°后向右平移一个单位得到的图案是( )
如图,四边形ABCD是正方形,点E在边DC上,点F在线段CB的延长线上,且
∠EAF=90°则△ADE变化到△ABF是通过( )
A.绕点A顺时针旋转180° B.绕点A顺时针旋转90°
C.绕点A逆时针旋转90° D.绕点A逆时针旋转180°
3.观察如图所示的图案,它可以看作是由一个基本图形绕中心连续旋转________次,且每次旋转__________度而得到的.
4.用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°,则三角板的斜边与射线OA的夹角a为___________.
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′顺时针旋转90°,得到
△A″B″C″.请你在图中画出△A′B′C′和△A″B″C″.
6.如图,△ABC是等边三角形,点D是BC边上一点.
(1)作出将△ABD绕点A逆时针旋转60°后的图形;
(2)如果点M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
7.如图,△ABC≌△DEF.△DEF能否由△ABC通过一次旋转得到?若能,请用直尺和圆规画出旋转中心,若不能,试简要说明理由.
8.如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )
4,30° B. 2,60° C. 1,30° D. 3,60?
9.(随州模拟)在等边△ABC中,D是AC上一点,连接BD,将△BCD绕点B逆时针旋转60得到△BAE,连接ED,若BC=5,BD=4,则下列结论错误的是( )
AE∥BC B. ∠ADE=∠BDC
C. △BDE是等边三角形 D. △ADE的周长是9
10.如图,小明将△ABC绕点O旋转得到△A′B′C′,其中点A′,B′,C′分别是A,B,C的对应点.随即又将△ABC的边AC,BC及旋转中心O及△ABC的位置找到,你认为可以吗?若可以,试确定旋转中心O及△ABC的位置;若不可以,请说明理由.
11.(1)如图1,在正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连接EF,AG.求证:EF=FG.
(2)如图2,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°若BM=1,CN=3,求MN的长.
温馨提示:解答第(2)题时,回忆一下第(1)题的解答方法.
参考答案
考点突破
例1 解:(1)连接OA,OB,OC;(2)分别以OA,OB,OC为一边作∠AOA′=∠BOB′=∠COC′=120°;(3)分别在射线OA′,OB′,OC′上截取OA′=OA,OB′=OB,OC′=OC;(4)连接A′B′,B′C′,C′A′,则△A′B′C′就是△ABC绕点O顺时针旋转120°后的图形。
题组训练
B 2. B
3.解:如图所示:
4.解:如图所示:
例2 解:∵BC=EF,∠B=60°,∴△BCE是等边三角形。
∴∠AFE=30°,∴∠GFD=60°。又∵∠D=∠A=30°,∴∠FGD=90°。
在Rt△DEF中,DE=AB=10 cm,∴EF=BC=AB=5 cm.
∴DF=(cm).∴FG=FD=(cm).
题组训练
5. A 6. 4 7. 55?
8. 解:(1)150?;(2)由CB = BD,可知△CBD是等腰三角形。
巩固练习
D 2. B
3. 3 90 4. 22?
5.解:如图所示:
解:(1)如图,△ACE即为所作图形。
点M转到了AC的中点位置上。
解:能,如下图,点O1就是所求作的旋转中心。
B 9. B
10,解:如图,连接AA', BB',分别作AA', BB'的中垂线相交于点O,则点O即为旋转中心,再作C′的对应点C,连接AC, BC,则△ABC的位置也就确定出来了.
解:(1)证明:∵四边形ABCD是正方形,
∴AB=AD, ∠B=∠ADF=∠ADG=∠BAD=90?.
又∵DG=BE,∴△ABE≌△ADG.∴AE=AG,∠BAE=∠DAG.
∵∠BAD=90?, ∠EAF=45?,∴∠BAE+∠FAD=45?。
∴∠DAG+∠FAD=45?,即∠FAG=∠FAE=45?.
又∵AF=AF,∴△AFE≌△AFG. ∴EF=FG.
(2)如图,将△ABM绕点A逆时针旋转90?,得到△ACD,则CD=BM=1,AM=AD,∠B=∠ACB=∠ACD=45?.连接ND,则∠NCD=90°.∵∠BAC=90°,∠MAN=45?,
∴∠BAM+∠CAN=45?,∴∠DAC+∠CAN=45?,即∠NAM=∠NAD=45?.
又∵AN=AN,∴△ANM≌△AND. ∴MN=ND.
在Rt△CDN中,由勾股定理,得ND=,∴MN=.
_21?????????è?????(www.21cnjy.com)_
