人教版数学八年级上册 12.2三角形全等的判定同步测试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学八年级上册 12.2三角形全等的判定同步测试题(一)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 209.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-05 19:12:04 | ||
图片预览

文档简介
三角形全等的判定同步测试题(一)
一.选择题
1.在下列各组条件中不能说明△ABC≌△DEF的是( )
A.AC=DF,BC=EF,∠A=∠D B.AB=DE,∠B=∠E,∠C=∠F
C.AB=DE,∠A=∠D,∠B=∠E D.AB=DE,BC=EF,AC=DF
2.如图,点E、F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是( )
A.AD∥BC B.DF∥BE C.∠A=∠C D.∠D=∠B
3.如图,已知AB=AC,D、E分别为AB、AC上的点,AD=AE,则下列结论不一定成立的是( )
A.∠B=∠C B.DB=EC C.DC=EB D.AD=DB
4.如图,△ABC中,∠B=∠C=65°,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )
A.75° B.70° C.65° D.60°
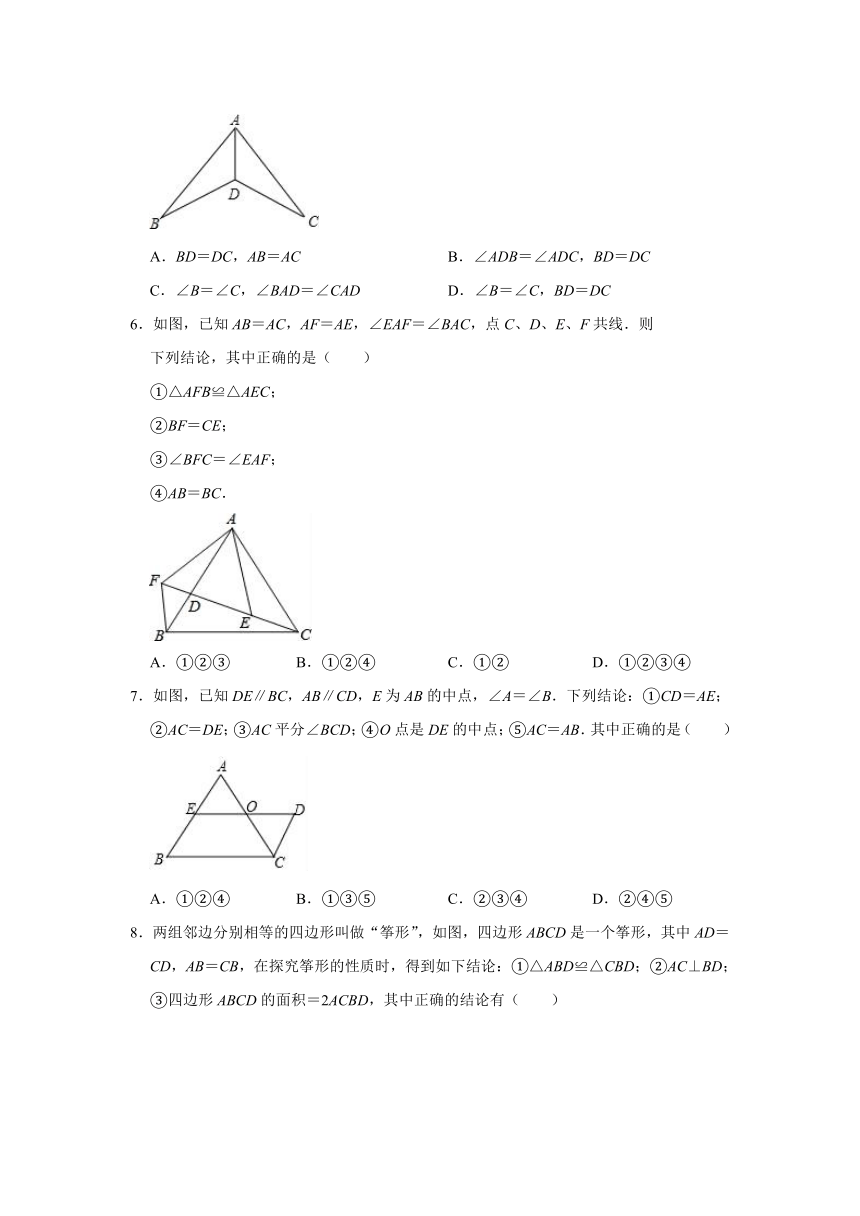
5.如图,下列条件中,不能证明△ABD≌△ACD的是( )
A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC
6.如图,已知AB=AC,AF=AE,∠EAF=∠BAC,点C、D、E、F共线.则
下列结论,其中正确的是( )
①△AFB≌△AEC;
②BF=CE;
③∠BFC=∠EAF;
④AB=BC.
A.①②③ B.①②④ C.①② D.①②③④
7.如图,已知DE∥BC,AB∥CD,E为AB的中点,∠A=∠B.下列结论:①CD=AE;②AC=DE;③AC平分∠BCD;④O点是DE的中点;⑤AC=AB.其中正确的是( )
A.①②④ B.①③⑤ C.②③④ D.②④⑤
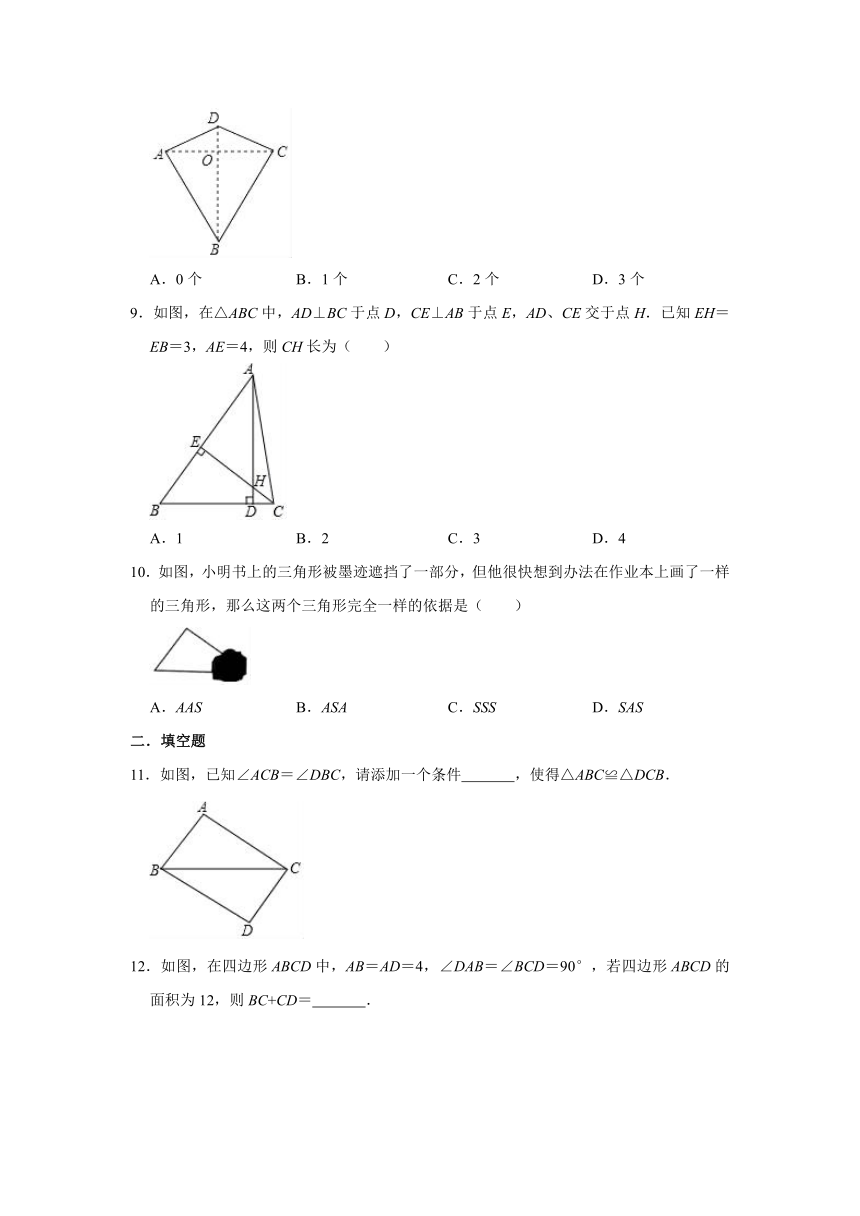
8.两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积=2ACBD,其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个
9.如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点E,AD、CE交于点H.已知EH=EB=3,AE=4,则CH长为( )
A.1 B.2 C.3 D.4
10.如图,小明书上的三角形被墨迹遮挡了一部分,但他很快想到办法在作业本上画了一样的三角形,那么这两个三角形完全一样的依据是( )
A.AAS B.ASA C.SSS D.SAS
二.填空题
11.如图,已知∠ACB=∠DBC,请添加一个条件 ,使得△ABC≌△DCB.
12.如图,在四边形ABCD中,AB=AD=4,∠DAB=∠BCD=90°,若四边形ABCD的面积为12,则BC+CD= .
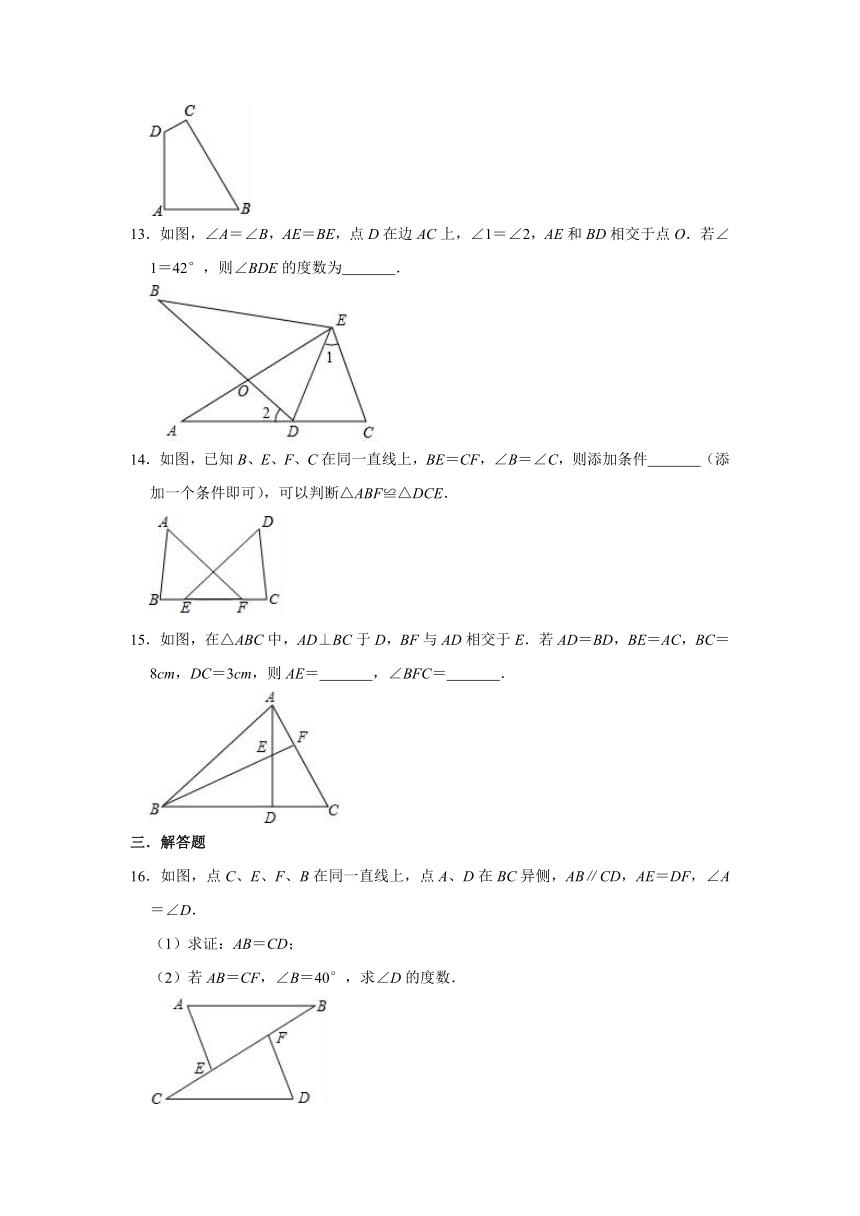
13.如图,∠A=∠B,AE=BE,点D在边AC上,∠1=∠2,AE和BD相交于点O.若∠1=42°,则∠BDE的度数为 .
14.如图,已知B、E、F、C在同一直线上,BE=CF,∠B=∠C,则添加条件 (添加一个条件即可),可以判断△ABF≌△DCE.
15.如图,在△ABC中,AD⊥BC于D,BF与AD相交于E.若AD=BD,BE=AC,BC=8cm,DC=3cm,则AE= ,∠BFC= .
三.解答题
16.如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.
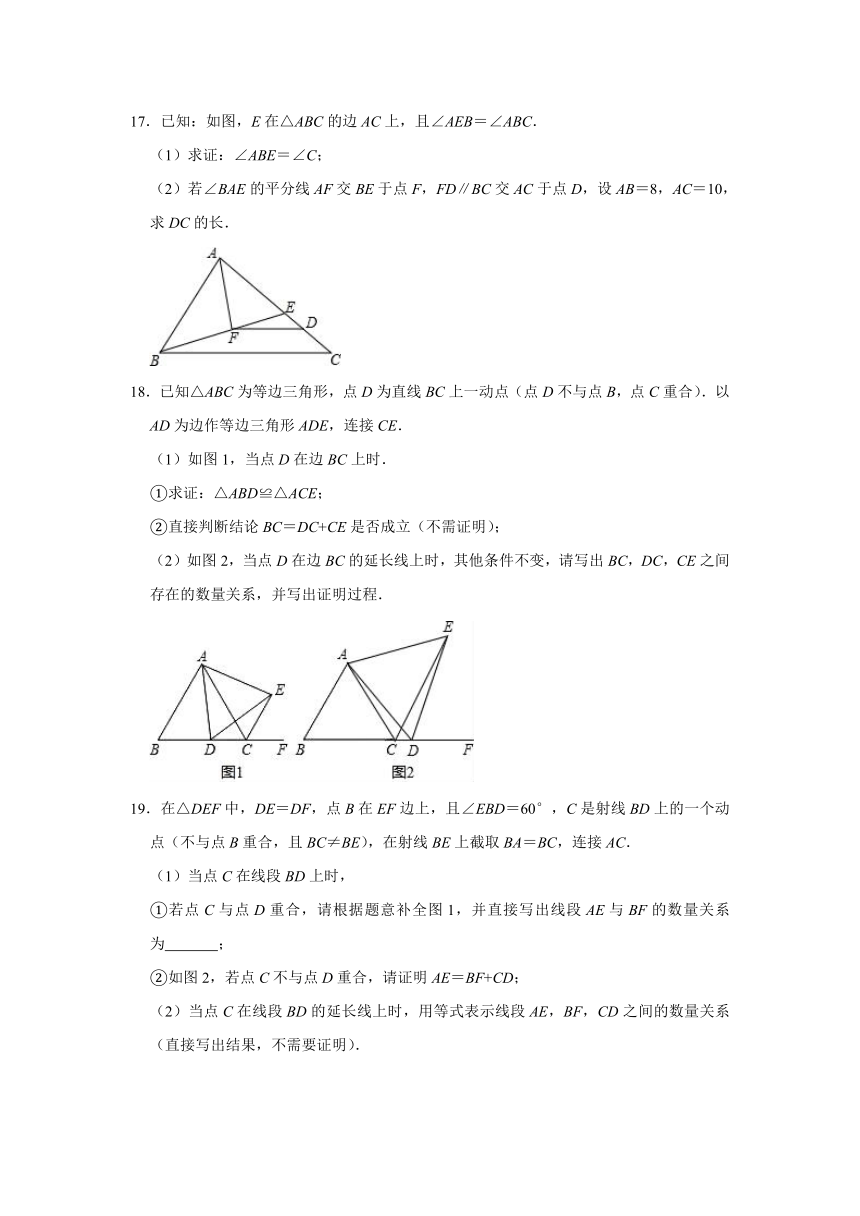
17.已知:如图,E在△ABC的边AC上,且∠AEB=∠ABC.
(1)求证:∠ABE=∠C;
(2)若∠BAE的平分线AF交BE于点F,FD∥BC交AC于点D,设AB=8,AC=10,求DC的长.
18.已知△ABC为等边三角形,点D为直线BC上一动点(点D不与点B,点C重合).以AD为边作等边三角形ADE,连接CE.
(1)如图1,当点D在边BC上时.
①求证:△ABD≌△ACE;
②直接判断结论BC=DC+CE是否成立(不需证明);
(2)如图2,当点D在边BC的延长线上时,其他条件不变,请写出BC,DC,CE之间存在的数量关系,并写出证明过程.
19.在△DEF中,DE=DF,点B在EF边上,且∠EBD=60°,C是射线BD上的一个动点(不与点B重合,且BC≠BE),在射线BE上截取BA=BC,连接AC.
(1)当点C在线段BD上时,
①若点C与点D重合,请根据题意补全图1,并直接写出线段AE与BF的数量关系为 ;
②如图2,若点C不与点D重合,请证明AE=BF+CD;
(2)当点C在线段BD的延长线上时,用等式表示线段AE,BF,CD之间的数量关系(直接写出结果,不需要证明).
参考答案与试题解析
一.选择题
1.【解答】解:A、AC=DF,BC=EF,∠A=∠D不能证明△ABC≌△DEF,故此选项符合题意;
B、AB=DE,∠B=∠E,∠C=∠F,可以利用AAS定理证明△ABC≌△DEF,故此选项不合题意;
C、AB=DE,∠A=∠D,∠B=∠E,可以利用ASA定理证明△ABC≌△DEF,故此选项不合题意;
D、AB=DE,BC=EF,AC=DF可以利用SSS定理证明△ABC≌△DEF,故此选项不合题意;
故选:A.
2.【解答】解:∠D=∠B,
理由是:∵在△ADF和△CBE中
,
∴△ADF≌△CBE(SAS),
即选项D正确;
具备选项A、选项B,选项C的条件都不能推出两三角形全等,
故选:D.
3.【解答】解:∵在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
A、由△ABE≌△ACD推知∠B=∠C,故本选项错误;
B、由△ABE≌△ACD推知AD=AE,则DB=EC,故本选项错误;
C、由△ABE≌△ACD推知DC=EB,故本选项错误;
D、由△ABE≌△ACD推知AD=AE,但是不能推出AD=BD,故本选项正确;
故选:D.
4.【解答】解:∵∠B=∠C=65°,BD=CE,BE=CF,
∴△DBE≌△ECF(SAS),
∴∠BDE=∠FEC,
∵∠BDE+∠BED=180°﹣65°=115°,
∴∠BED+∠CEF=115°,
∴∠DEF=180°﹣115°=65°,
故选:C.
5.【解答】解:A、依据SSS可知△ABD≌△ACD,故A不符合要求;
B、依据SAS可知△ABD≌△ACD,故B不符合要求;
C、依据AAS可知△ABD≌△ACD,故C不符合要求;
D、依据SSA可知△ABD≌△ACD,故D符合要求.
故选:D.
6.【解答】解:∵∠EAF=∠BAC,
∴∠BAF=∠CAE,
∵AF=AE,AB=AC,
∴△FAB≌△EAC(SAS),故①正确,
∴BF=EC,故②正确,
∴∠ABF=∠ACE,
∵∠BDF=∠ADC,
∴∠BFC=∠DAC,∵∠DAC=∠EAF,
∴∠BFC=∠EAF,故③正确,
无法判断AB=BC,故④错误,
故选:A.
7.【解答】解:①∵DE∥BC,AB∥CD,
∴四边形BCDE为平行四边形,
∴CD=BE.
又∵E为AB的中点,
∴AE=BE=CD,结论①正确;
②∵∠A=∠B,
∴AC=BC.
∵四边形BCDE为平行四边形,
∴DE=BC,
∴AC=DE,结论②正确;
③已知条件无法证出∠ACB=∠ACD,
∴无法得出AC平分∠BCD,结论③错误;
④∵AB∥CD,
∴∠A=∠OCD.
在△AOE和△COD中,,
∴△AOE≌△COD(AAS),
∴EO=DO,
∴O点是DE的中点,结论④正确;
⑤已知条件无法证出AC=AB,结论⑤错误.
故选:A.
8.【解答】解:在△ABD与△CBD中,
,
∴△ABD≌△CBD(SSS),故①正确;
∴∠ADB=∠CDB,
在△AOD与△COD中,
,
∴△AOD≌△COD(SAS),
∴∠AOD=∠COD=90°,AO=OC,
∴AC⊥DB,故②正确;
四边形ABCD的面积=S△ABD+S△BDC=ACBD,故③错误;
故选:C.
9.【解答】解:在△ABC中,AD⊥BC,CE⊥AB,
∴∠AEH=∠ADB=90°;
∵∠EAH+∠AHE=90°,∠DHC+∠BCH=90°,
∵∠EHA=∠DHC(对顶角相等),
∴∠EAH=∠DCH(等量代换);
在△BCE和△HAE中,
,
∴△AEH≌△CEB(AAS);
∴AE=CE;
∵EH=EB=3,AE=4,
∴CH=CE﹣EH=AE﹣EH=4﹣3=1.
故选:A.
10.【解答】解:由图可知,三角形两角及夹边可以作出,
所以,依据是ASA.
故选:B.
二.填空题(共5小题)
11.【解答】解:可以添加AC=BD,利用SAS判定其全等;
故答案为:AC=BD.
12.【解答】解:直角△ABD中,AB=AD=4,则△ABD面积S=×4×4=8,且BD2=32,
∵四边形ABCD的面积为12,
∴△BCD的面积为12﹣8=4,
∴×BC×CD=4,∴BC×CD=8,
在直角△CBD中,BC2+CD2=BD2
∴(BC+CD)2=BC2+CD2+2×BC×CD=BD2+2×BC×CD=32+16=48,
故BC+CD=.
故答案为4.
13.【解答】证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA),
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=42°,
∴∠C=∠EDC=69°,
∴∠BDE=∠C=69°.
故答案为69°.
14.【解答】解:∵BE=CF,
∴BF=CE,
又∵∠B=∠C,
∴当AB=DC时,依据SAS可得△ABF≌△DCE.
当∠AFB=∠DEC时,依据ASA可得△ABF≌△DCE.
当∠A=∠D时,依据AAS可得△ABF≌△DCE.
故答案为:AB=CD或∠AFB=∠DEC或∠A=∠D.
15.【解答】解:∵AD⊥BC,
∴∠BDE=∠ADC=90°,
∵BD=AD,BE=AC,
∴Rt△BDE≌Rt△ADC(HL),
∴CD=DE=3cm,∠DBE=∠DAC,
∵BC=AD=BC﹣AD=5cm,
∴AE=AD﹣DE=2cm,
∵∠AEF=∠BED∠EAF=∠DBE,
∴∠AFE=∠BDE=90°,
∴∠BFC=90°,
故答案为2cm,90°.
三.解答题(共4小题)
16.【解答】(1)证明:∵AB∥CD,
∴∠B=∠C,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(AAS),
∴AB=CD;
(2)解:∵△ABE≌△DCF,
∴AB=CD,BE=CF,∠B=∠C,
∵∠B=40°,
∴∠C=40°
∵AB=CF,
∴CF=CD,
∴∠D=∠CFD=(180°﹣40°)=70°.
17.【解答】(1)证明:在△ABE中,∠ABE=180°﹣∠BAE﹣∠AEB,
在△ABC中,∠C=180°﹣∠BAC﹣∠ABC,
∵∠AEB=∠ABC,∠BAE=∠BAC,
∴∠ABE=∠C;
(2)解:∵FD∥BC,
∴∠ADF=∠C,
又∠ABE=∠C,
∴∠ABE=∠ADF,
∵AF平分∠BAE,
∴∠BAF=∠DAF,
在△ABF和△ADF中,
,
∴△ABF≌△ADF(AAS),
∴AB=AD,
∵AB=8,AC=10,
∴DC=AC﹣AD=AC﹣AB=10﹣8=2.
18.【解答】解:(1)①∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE.
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠EAC.
在△ABD和△ACE中
,
∴△ABD≌△ACE(SAS).
②∵△ABD≌△ACE,
∴BD=CE.
∵BC=BD+CD,
∴BC=CE+CD.
(2)BC+CD=CE.
∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE.
∴∠BAC+∠DAC=∠DAE+∠DAC,
∴∠BAD=∠EAC.
在△ABD和△ACE中
,
∴△ABD≌△ACE(SAS).
∴BD=CE.
∵BD=BC+CD,
∴CE=BC+CD;
19.【解答】解:(1)①如图1,∵BA=BC,∠EBD=60°,
∴△ABC是等边三角形,
∴AD=AB=BC,∠DAB=∠ABC=60°,
∴∠EAD=∠FBD=120°,
∵DE=DF,
∴∠E=∠F,
在△AEC与△BCF中,,
∴△ADE≌△BDF(AAS),
∴AE=BF;
故答案为:AE=BF;
②证明:在BE上截取BG=BD,连接DG,
∵∠EBD=60°,BG=BD,
∴△GBD是等边三角形.
同理,△ABC也是等边三角形.
∴AG=CD,
∵DE=DF,∴∠E=∠F.
又∵∠DGB=∠DBG=60°,
∴∠DGE=∠DBF=120°,
在△DGE与△DBF中,,
∴△DGE≌△DBF(AAS),
∴GE=BF,
∴AE=BF+CD;
(2)如图3,连接DG,
由(1)知,GE=BF,AG=CD,
∴AE=EG﹣AG;
∴AE=BF﹣CD,
如图4,连接DG,
由(1)知,GE=BF,AG=CD,
∴AE=AG﹣EG;
∴AE=CD﹣BF
一.选择题
1.在下列各组条件中不能说明△ABC≌△DEF的是( )
A.AC=DF,BC=EF,∠A=∠D B.AB=DE,∠B=∠E,∠C=∠F
C.AB=DE,∠A=∠D,∠B=∠E D.AB=DE,BC=EF,AC=DF
2.如图,点E、F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是( )
A.AD∥BC B.DF∥BE C.∠A=∠C D.∠D=∠B
3.如图,已知AB=AC,D、E分别为AB、AC上的点,AD=AE,则下列结论不一定成立的是( )
A.∠B=∠C B.DB=EC C.DC=EB D.AD=DB
4.如图,△ABC中,∠B=∠C=65°,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )
A.75° B.70° C.65° D.60°
5.如图,下列条件中,不能证明△ABD≌△ACD的是( )
A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC
6.如图,已知AB=AC,AF=AE,∠EAF=∠BAC,点C、D、E、F共线.则
下列结论,其中正确的是( )
①△AFB≌△AEC;
②BF=CE;
③∠BFC=∠EAF;
④AB=BC.
A.①②③ B.①②④ C.①② D.①②③④
7.如图,已知DE∥BC,AB∥CD,E为AB的中点,∠A=∠B.下列结论:①CD=AE;②AC=DE;③AC平分∠BCD;④O点是DE的中点;⑤AC=AB.其中正确的是( )
A.①②④ B.①③⑤ C.②③④ D.②④⑤
8.两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积=2ACBD,其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个
9.如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点E,AD、CE交于点H.已知EH=EB=3,AE=4,则CH长为( )
A.1 B.2 C.3 D.4
10.如图,小明书上的三角形被墨迹遮挡了一部分,但他很快想到办法在作业本上画了一样的三角形,那么这两个三角形完全一样的依据是( )
A.AAS B.ASA C.SSS D.SAS
二.填空题
11.如图,已知∠ACB=∠DBC,请添加一个条件 ,使得△ABC≌△DCB.
12.如图,在四边形ABCD中,AB=AD=4,∠DAB=∠BCD=90°,若四边形ABCD的面积为12,则BC+CD= .
13.如图,∠A=∠B,AE=BE,点D在边AC上,∠1=∠2,AE和BD相交于点O.若∠1=42°,则∠BDE的度数为 .
14.如图,已知B、E、F、C在同一直线上,BE=CF,∠B=∠C,则添加条件 (添加一个条件即可),可以判断△ABF≌△DCE.
15.如图,在△ABC中,AD⊥BC于D,BF与AD相交于E.若AD=BD,BE=AC,BC=8cm,DC=3cm,则AE= ,∠BFC= .
三.解答题
16.如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.
17.已知:如图,E在△ABC的边AC上,且∠AEB=∠ABC.
(1)求证:∠ABE=∠C;
(2)若∠BAE的平分线AF交BE于点F,FD∥BC交AC于点D,设AB=8,AC=10,求DC的长.
18.已知△ABC为等边三角形,点D为直线BC上一动点(点D不与点B,点C重合).以AD为边作等边三角形ADE,连接CE.
(1)如图1,当点D在边BC上时.
①求证:△ABD≌△ACE;
②直接判断结论BC=DC+CE是否成立(不需证明);
(2)如图2,当点D在边BC的延长线上时,其他条件不变,请写出BC,DC,CE之间存在的数量关系,并写出证明过程.
19.在△DEF中,DE=DF,点B在EF边上,且∠EBD=60°,C是射线BD上的一个动点(不与点B重合,且BC≠BE),在射线BE上截取BA=BC,连接AC.
(1)当点C在线段BD上时,
①若点C与点D重合,请根据题意补全图1,并直接写出线段AE与BF的数量关系为 ;
②如图2,若点C不与点D重合,请证明AE=BF+CD;
(2)当点C在线段BD的延长线上时,用等式表示线段AE,BF,CD之间的数量关系(直接写出结果,不需要证明).
参考答案与试题解析
一.选择题
1.【解答】解:A、AC=DF,BC=EF,∠A=∠D不能证明△ABC≌△DEF,故此选项符合题意;
B、AB=DE,∠B=∠E,∠C=∠F,可以利用AAS定理证明△ABC≌△DEF,故此选项不合题意;
C、AB=DE,∠A=∠D,∠B=∠E,可以利用ASA定理证明△ABC≌△DEF,故此选项不合题意;
D、AB=DE,BC=EF,AC=DF可以利用SSS定理证明△ABC≌△DEF,故此选项不合题意;
故选:A.
2.【解答】解:∠D=∠B,
理由是:∵在△ADF和△CBE中
,
∴△ADF≌△CBE(SAS),
即选项D正确;
具备选项A、选项B,选项C的条件都不能推出两三角形全等,
故选:D.
3.【解答】解:∵在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
A、由△ABE≌△ACD推知∠B=∠C,故本选项错误;
B、由△ABE≌△ACD推知AD=AE,则DB=EC,故本选项错误;
C、由△ABE≌△ACD推知DC=EB,故本选项错误;
D、由△ABE≌△ACD推知AD=AE,但是不能推出AD=BD,故本选项正确;
故选:D.
4.【解答】解:∵∠B=∠C=65°,BD=CE,BE=CF,
∴△DBE≌△ECF(SAS),
∴∠BDE=∠FEC,
∵∠BDE+∠BED=180°﹣65°=115°,
∴∠BED+∠CEF=115°,
∴∠DEF=180°﹣115°=65°,
故选:C.
5.【解答】解:A、依据SSS可知△ABD≌△ACD,故A不符合要求;
B、依据SAS可知△ABD≌△ACD,故B不符合要求;
C、依据AAS可知△ABD≌△ACD,故C不符合要求;
D、依据SSA可知△ABD≌△ACD,故D符合要求.
故选:D.
6.【解答】解:∵∠EAF=∠BAC,
∴∠BAF=∠CAE,
∵AF=AE,AB=AC,
∴△FAB≌△EAC(SAS),故①正确,
∴BF=EC,故②正确,
∴∠ABF=∠ACE,
∵∠BDF=∠ADC,
∴∠BFC=∠DAC,∵∠DAC=∠EAF,
∴∠BFC=∠EAF,故③正确,
无法判断AB=BC,故④错误,
故选:A.
7.【解答】解:①∵DE∥BC,AB∥CD,
∴四边形BCDE为平行四边形,
∴CD=BE.
又∵E为AB的中点,
∴AE=BE=CD,结论①正确;
②∵∠A=∠B,
∴AC=BC.
∵四边形BCDE为平行四边形,
∴DE=BC,
∴AC=DE,结论②正确;
③已知条件无法证出∠ACB=∠ACD,
∴无法得出AC平分∠BCD,结论③错误;
④∵AB∥CD,
∴∠A=∠OCD.
在△AOE和△COD中,,
∴△AOE≌△COD(AAS),
∴EO=DO,
∴O点是DE的中点,结论④正确;
⑤已知条件无法证出AC=AB,结论⑤错误.
故选:A.
8.【解答】解:在△ABD与△CBD中,
,
∴△ABD≌△CBD(SSS),故①正确;
∴∠ADB=∠CDB,
在△AOD与△COD中,
,
∴△AOD≌△COD(SAS),
∴∠AOD=∠COD=90°,AO=OC,
∴AC⊥DB,故②正确;
四边形ABCD的面积=S△ABD+S△BDC=ACBD,故③错误;
故选:C.
9.【解答】解:在△ABC中,AD⊥BC,CE⊥AB,
∴∠AEH=∠ADB=90°;
∵∠EAH+∠AHE=90°,∠DHC+∠BCH=90°,
∵∠EHA=∠DHC(对顶角相等),
∴∠EAH=∠DCH(等量代换);
在△BCE和△HAE中,
,
∴△AEH≌△CEB(AAS);
∴AE=CE;
∵EH=EB=3,AE=4,
∴CH=CE﹣EH=AE﹣EH=4﹣3=1.
故选:A.
10.【解答】解:由图可知,三角形两角及夹边可以作出,
所以,依据是ASA.
故选:B.
二.填空题(共5小题)
11.【解答】解:可以添加AC=BD,利用SAS判定其全等;
故答案为:AC=BD.
12.【解答】解:直角△ABD中,AB=AD=4,则△ABD面积S=×4×4=8,且BD2=32,
∵四边形ABCD的面积为12,
∴△BCD的面积为12﹣8=4,
∴×BC×CD=4,∴BC×CD=8,
在直角△CBD中,BC2+CD2=BD2
∴(BC+CD)2=BC2+CD2+2×BC×CD=BD2+2×BC×CD=32+16=48,
故BC+CD=.
故答案为4.
13.【解答】证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA),
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=42°,
∴∠C=∠EDC=69°,
∴∠BDE=∠C=69°.
故答案为69°.
14.【解答】解:∵BE=CF,
∴BF=CE,
又∵∠B=∠C,
∴当AB=DC时,依据SAS可得△ABF≌△DCE.
当∠AFB=∠DEC时,依据ASA可得△ABF≌△DCE.
当∠A=∠D时,依据AAS可得△ABF≌△DCE.
故答案为:AB=CD或∠AFB=∠DEC或∠A=∠D.
15.【解答】解:∵AD⊥BC,
∴∠BDE=∠ADC=90°,
∵BD=AD,BE=AC,
∴Rt△BDE≌Rt△ADC(HL),
∴CD=DE=3cm,∠DBE=∠DAC,
∵BC=AD=BC﹣AD=5cm,
∴AE=AD﹣DE=2cm,
∵∠AEF=∠BED∠EAF=∠DBE,
∴∠AFE=∠BDE=90°,
∴∠BFC=90°,
故答案为2cm,90°.
三.解答题(共4小题)
16.【解答】(1)证明:∵AB∥CD,
∴∠B=∠C,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(AAS),
∴AB=CD;
(2)解:∵△ABE≌△DCF,
∴AB=CD,BE=CF,∠B=∠C,
∵∠B=40°,
∴∠C=40°
∵AB=CF,
∴CF=CD,
∴∠D=∠CFD=(180°﹣40°)=70°.
17.【解答】(1)证明:在△ABE中,∠ABE=180°﹣∠BAE﹣∠AEB,
在△ABC中,∠C=180°﹣∠BAC﹣∠ABC,
∵∠AEB=∠ABC,∠BAE=∠BAC,
∴∠ABE=∠C;
(2)解:∵FD∥BC,
∴∠ADF=∠C,
又∠ABE=∠C,
∴∠ABE=∠ADF,
∵AF平分∠BAE,
∴∠BAF=∠DAF,
在△ABF和△ADF中,
,
∴△ABF≌△ADF(AAS),
∴AB=AD,
∵AB=8,AC=10,
∴DC=AC﹣AD=AC﹣AB=10﹣8=2.
18.【解答】解:(1)①∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE.
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠EAC.
在△ABD和△ACE中
,
∴△ABD≌△ACE(SAS).
②∵△ABD≌△ACE,
∴BD=CE.
∵BC=BD+CD,
∴BC=CE+CD.
(2)BC+CD=CE.
∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE.
∴∠BAC+∠DAC=∠DAE+∠DAC,
∴∠BAD=∠EAC.
在△ABD和△ACE中
,
∴△ABD≌△ACE(SAS).
∴BD=CE.
∵BD=BC+CD,
∴CE=BC+CD;
19.【解答】解:(1)①如图1,∵BA=BC,∠EBD=60°,
∴△ABC是等边三角形,
∴AD=AB=BC,∠DAB=∠ABC=60°,
∴∠EAD=∠FBD=120°,
∵DE=DF,
∴∠E=∠F,
在△AEC与△BCF中,,
∴△ADE≌△BDF(AAS),
∴AE=BF;
故答案为:AE=BF;
②证明:在BE上截取BG=BD,连接DG,
∵∠EBD=60°,BG=BD,
∴△GBD是等边三角形.
同理,△ABC也是等边三角形.
∴AG=CD,
∵DE=DF,∴∠E=∠F.
又∵∠DGB=∠DBG=60°,
∴∠DGE=∠DBF=120°,
在△DGE与△DBF中,,
∴△DGE≌△DBF(AAS),
∴GE=BF,
∴AE=BF+CD;
(2)如图3,连接DG,
由(1)知,GE=BF,AG=CD,
∴AE=EG﹣AG;
∴AE=BF﹣CD,
如图4,连接DG,
由(1)知,GE=BF,AG=CD,
∴AE=AG﹣EG;
∴AE=CD﹣BF
