浙江省台州市四校2012届高三第一次联考理科数学试卷
文档属性
| 名称 | 浙江省台州市四校2012届高三第一次联考理科数学试卷 |
|
|
| 格式 | zip | ||
| 文件大小 | 271.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-07 00:00:00 | ||
图片预览




文档简介
浙江省台州市四校2012届高三第一次联考理科数学试卷
选择题:本大题共10小题,每小题5分,满分50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设是非空集合,定义={且},己知
,则等于 ( )
A.(2,+∞) B.[0,1]∪[2,+∞)
C.[0,1)∪(2,+∞) D.[0,1]∪(2,+∞)
2. 已知命题:抛物线的准线方程为;命题:若函数为
偶函数,则关于对称.则下列命题是真命题的是 ( )
A. B. C. D.
3.已知cos(α-)+sinα= ( )
A.- B . C. - D.
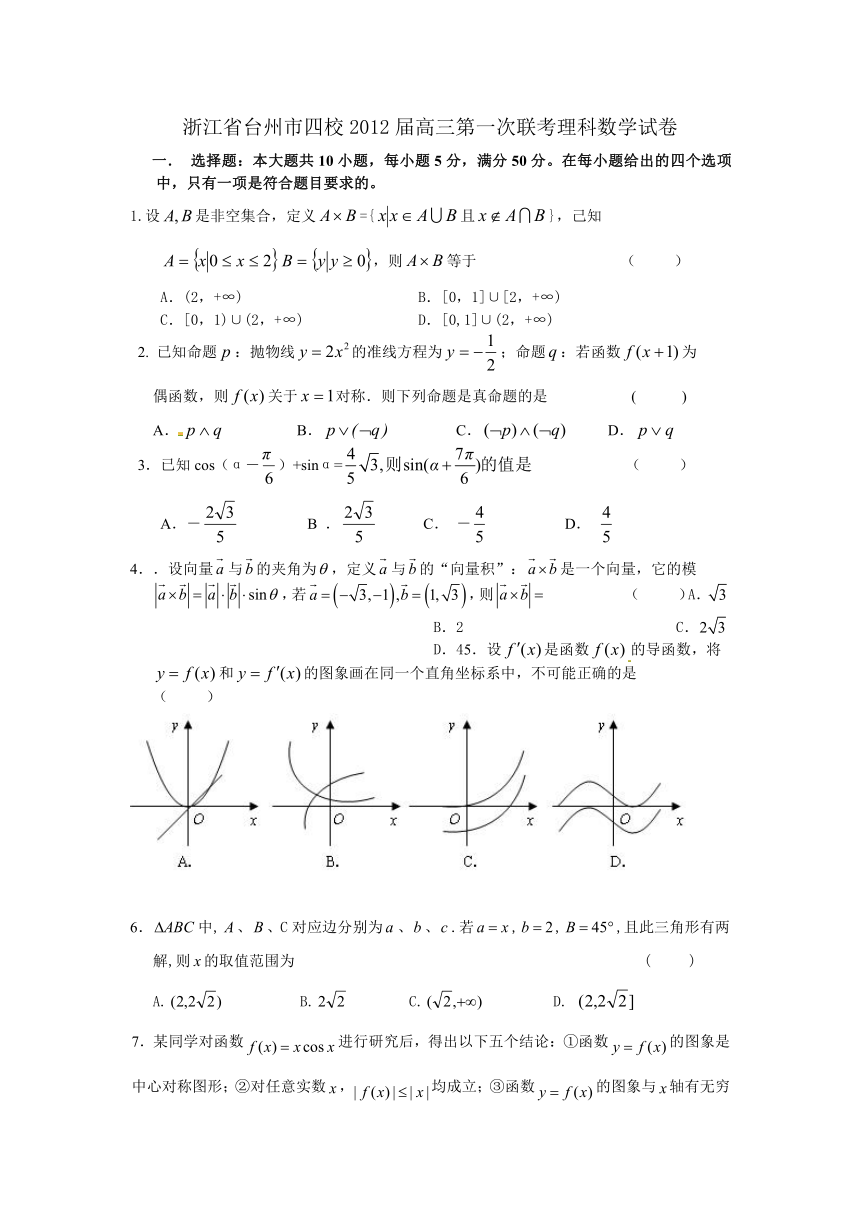
4..设向量与的夹角为,定义与的“向量积”:是一个向量,它的模,若,则 ( )A. B.2 C. D.45.设是函数的导函数,将和的图象画在同一个直角坐标系中,不可能正确的是 ( )
6.中,、、C对应边分别为、、.若,,,且此三角形有两解,则的取值范围为 ( )
A. B. C. D.
7.某同学对函数进行研究后,得出以下五个结论:①函数的图象是中心对称图形;②对任意实数,均成立;③函数的图象与轴有无穷多个公共点,且任意相邻两点的距离相等;④函数的图象与直线有无穷多个公共点,且任意相邻两点的距离相等;⑤当常数满足时,函数的图象与直线有且仅有一个公共点。其中所有正确结论的序号是 ( )
A.①②④ B.①②③④ C.①②④⑤ D.①②③④⑤
8.在直角梯形ABCD中,,动点P在以点C为圆心,且与直线BD相切的圆内运动,设,则的取值范围是 ( )
A. B. C. D.
9.若长度为定值的线段AB的两端点分别在x轴正半轴和y轴正半轴上移动,O为坐标原点,则的重心、内心、外心、垂心的轨迹都不可能是 ( )
A.点 B.线段 C 圆弧 D.抛物线的一部分
10.已知函数的零点个数为( )
A.7 B.6 C.5 D.4
二、填空题:本大题共7小题,每小题4分,满分28分。
11.已知a,b,c为△ABC的三个内角A,B,C的对边,向量m=(),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角B=____▲_____
12.已知函数是定义在上的增函数,函数的图象关于点(1 , 0)对称,若对任意的,不等式恒成立,则当时,的取值范围是____▲_____
13.设为三个非零向量,且,
则的最大值是____▲_____.
14.观察下列几个三角恒等式:
①;
②;
③.
一般地,若都有意义,你从这三个恒等式中猜想得到的一个结论为 ▲
15.如图,已知是椭圆 的左、右焦点, 点在椭圆上,线段与圆相切于点,
且点为线段的中点,则椭圆的离心率为 ▲ .
16.已知函数,,
设,且函数的零点均在区间内,
则的最小值为____▲_____.
17.已知对任意平面向量=(x,y),把绕其起点沿逆时针方向旋转角得到向量
,叫做把点B绕点A逆时针方向旋转角
得到点P. 设平面内曲线C上的每一点绕原点沿逆时针方向旋转后得到点的轨迹是
曲线,则原来曲线C的方程是____▲_____
三、解答题:本大题共5小题,满分72分。解答须写出文字说明,证明过程和演算步骤
18、(本题满分14分)
已知集合,
(Ⅰ)当时,求;
(Ⅱ)求使的实数的取值范围。
19、(本题满分14分)
已知:函数的最大值为,最小正周期为.
(Ⅰ)求:的解析式;
(Ⅱ)若的三条边为,,,满足,边所对的角为.求:角的取值范围及函数的值域.
20 、(本题满分14分)
已知函数 HYPERLINK "http://www./" EMBED Equation.3 ,, HYPERLINK "http://www./" EMBED Equation.3
(Ⅰ)当时,若 HYPERLINK "http://www./" EMBED Equation.3 在上单调递增,求 HYPERLINK "http://www./" EMBED Equation.3 的取值范围;
(Ⅱ)求满足下列条件的所有实数对:当 HYPERLINK "http://www./" EMBED Equation.3 是整数时,存在,使得 HYPERLINK "http://www./" EMBED Equation.3 是的最大值, HYPERLINK "http://www./" EMBED Equation.3 是的最小值;
(Ⅲ)对满足(Ⅱ)的条件的一个实数对 HYPERLINK "http://www./" EMBED Equation.3 ,试构造一个定义在,且 HYPERLINK "http://www./" EMBED Equation.3 上的函数,使当 HYPERLINK "http://www./" EMBED Equation.3 时,,当 HYPERLINK "http://www./" EMBED Equation.3 时,取得最大值的自变量的值构成以 HYPERLINK "http://www./" EMBED Equation.3 为首项的等差数列。
21、(本小题满分14分)
椭圆过点P,且离心率为,F为椭圆的右焦点,、两点在椭圆上,且 ,定点(-4,0).
(Ⅰ)求椭圆C的方程;
(Ⅱ)当时 ,问:MN与AF是否垂直;
并证明你的结论.
(Ⅲ)当、两点在上运动,
且 =6时,
求直线MN的方程.
22、(本小题满分15分)
已知函数在上为增函数,且,为常数,.
(Ⅰ)求的值;
(Ⅱ)若在上为单调函数,求m的取值范围;
(Ⅲ)设,若在上至少存在一个,使得成立,求的m取值范围.
2011年台州市四校联考数学(理科)答案
一、选择题(每小题5分,共50分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A D C B D A C D D B
二、填空题(每小题4分,共28分)
11. 12. (13,49) 13. 14.
15. 16. 9 17.
三、解答题(共72分)
(18)(本题满分l4分)
解:(Ⅰ)当 …………………6分
(Ⅱ)时, ;时,
①当时,要使必须
②当时,,所以使的不存在,
③,要使,必须
综上可知,使的实数的范围为 ……………………14分
(19)(本题满分l4分)
(Ⅰ),
由,得………………2分
由及,得………………4分
…………6分
(Ⅱ).………………8分
为三角形内角,所以………………10分
,,…………14分
(20)(本题满分14分)
解:(Ⅰ)当时, HYPERLINK "http://www./" EMBED Equation.3 ,
若, HYPERLINK "http://www./" EMBED Equation.3 ,则在 HYPERLINK "http://www./" EMBED Equation.3 上单调递减,不符题意。
故,要使 HYPERLINK "http://www./" EMBED Equation.3 在上单调递增,必须满足 HYPERLINK "http://www./" EMBED Equation.3 ,∴ 。 (4分)
(Ⅱ)若 HYPERLINK "http://www./" EMBED Equation.3 ,,则 HYPERLINK "http://www./" EMBED Equation.3 无最大值,故,∴ HYPERLINK "http://www./" EMBED Equation.3 为二次函数,
要使有最大值,必须满足 HYPERLINK "http://www./" EMBED Equation.3 ,即且 HYPERLINK "http://www./" EMBED Equation.3 ,
此时,时, HYPERLINK "http://www./" EMBED Equation.3 有最大值。
又取最小值时, HYPERLINK "http://www./" EMBED Equation.3 ,依题意,有,则 HYPERLINK "http://www./" EMBED Equation.3 ,
∵且 HYPERLINK "http://www./" EMBED Equation.3 ,∴,得 HYPERLINK "http://www./" EMBED Equation.3 ,此时或 HYPERLINK "http://www./" EMBED Equation.3 。
∴满足条件的实数对是 HYPERLINK "http://www./" EMBED Equation.3 。 (9分)
(Ⅲ)当实数对是 HYPERLINK "http://www./" EMBED Equation.3 时, (14分)
依题意,只需构造以2(或2的正整数倍)为周期的周期函数即可。
如对 HYPERLINK "http://www./" EMBED Equation.3 ,,
此时, HYPERLINK "http://www./" EMBED Equation.3 ,
故
21,解:(Ⅰ)椭圆的离心率为
即可得 --2分
又椭圆过点P
解得,,椭圆C的方程为----- -----------4分
(Ⅱ)设,
则,
当时,, -----------5分
由M,N两点在椭圆上,
---------6分
若,则(舍去), ------------7分
. ------------8分
(Ⅲ)因为=6.--9分
由已知点F(2,0), 所以|AF|=6, 即得|yM-yN|= ------------10分
当MN轴时,故直线的斜率存在. ------------11分
不妨设直线MN的方程为:-----
联立、得 ------------12分
||=解得 ------------14分
此时,直线MN的方程为或 ------------15分
(22)(本题满分15分)
解:(1)由题意:在上恒成立,即,
在上恒成立,
只需sin…………(4分)
(2) 由(1),得f(x)-g(x)=mx-,,由于f(x)-g(x)在其定义域内为单调函数,则在上恒成立,即在上恒成立,故,综上,m的取值范围是 …………(9分)
(3)构造函数F(x)=f(x)-g(x)-h(x),,
当由得,,所以在上不存在一个,使得; …………(12分)
当m>0时,,因为,所以在上恒成立,故F(x)在上单调递增,,故m的取值范围是…………………………………………………………………………(15分)
另法:(3) 令
第21题
第21题
选择题:本大题共10小题,每小题5分,满分50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设是非空集合,定义={且},己知
,则等于 ( )
A.(2,+∞) B.[0,1]∪[2,+∞)
C.[0,1)∪(2,+∞) D.[0,1]∪(2,+∞)
2. 已知命题:抛物线的准线方程为;命题:若函数为
偶函数,则关于对称.则下列命题是真命题的是 ( )
A. B. C. D.
3.已知cos(α-)+sinα= ( )
A.- B . C. - D.
4..设向量与的夹角为,定义与的“向量积”:是一个向量,它的模,若,则 ( )A. B.2 C. D.45.设是函数的导函数,将和的图象画在同一个直角坐标系中,不可能正确的是 ( )
6.中,、、C对应边分别为、、.若,,,且此三角形有两解,则的取值范围为 ( )
A. B. C. D.
7.某同学对函数进行研究后,得出以下五个结论:①函数的图象是中心对称图形;②对任意实数,均成立;③函数的图象与轴有无穷多个公共点,且任意相邻两点的距离相等;④函数的图象与直线有无穷多个公共点,且任意相邻两点的距离相等;⑤当常数满足时,函数的图象与直线有且仅有一个公共点。其中所有正确结论的序号是 ( )
A.①②④ B.①②③④ C.①②④⑤ D.①②③④⑤
8.在直角梯形ABCD中,,动点P在以点C为圆心,且与直线BD相切的圆内运动,设,则的取值范围是 ( )
A. B. C. D.
9.若长度为定值的线段AB的两端点分别在x轴正半轴和y轴正半轴上移动,O为坐标原点,则的重心、内心、外心、垂心的轨迹都不可能是 ( )
A.点 B.线段 C 圆弧 D.抛物线的一部分
10.已知函数的零点个数为( )
A.7 B.6 C.5 D.4
二、填空题:本大题共7小题,每小题4分,满分28分。
11.已知a,b,c为△ABC的三个内角A,B,C的对边,向量m=(),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角B=____▲_____
12.已知函数是定义在上的增函数,函数的图象关于点(1 , 0)对称,若对任意的,不等式恒成立,则当时,的取值范围是____▲_____
13.设为三个非零向量,且,
则的最大值是____▲_____.
14.观察下列几个三角恒等式:
①;
②;
③.
一般地,若都有意义,你从这三个恒等式中猜想得到的一个结论为 ▲
15.如图,已知是椭圆 的左、右焦点, 点在椭圆上,线段与圆相切于点,
且点为线段的中点,则椭圆的离心率为 ▲ .
16.已知函数,,
设,且函数的零点均在区间内,
则的最小值为____▲_____.
17.已知对任意平面向量=(x,y),把绕其起点沿逆时针方向旋转角得到向量
,叫做把点B绕点A逆时针方向旋转角
得到点P. 设平面内曲线C上的每一点绕原点沿逆时针方向旋转后得到点的轨迹是
曲线,则原来曲线C的方程是____▲_____
三、解答题:本大题共5小题,满分72分。解答须写出文字说明,证明过程和演算步骤
18、(本题满分14分)
已知集合,
(Ⅰ)当时,求;
(Ⅱ)求使的实数的取值范围。
19、(本题满分14分)
已知:函数的最大值为,最小正周期为.
(Ⅰ)求:的解析式;
(Ⅱ)若的三条边为,,,满足,边所对的角为.求:角的取值范围及函数的值域.
20 、(本题满分14分)
已知函数 HYPERLINK "http://www./" EMBED Equation.3 ,, HYPERLINK "http://www./" EMBED Equation.3
(Ⅰ)当时,若 HYPERLINK "http://www./" EMBED Equation.3 在上单调递增,求 HYPERLINK "http://www./" EMBED Equation.3 的取值范围;
(Ⅱ)求满足下列条件的所有实数对:当 HYPERLINK "http://www./" EMBED Equation.3 是整数时,存在,使得 HYPERLINK "http://www./" EMBED Equation.3 是的最大值, HYPERLINK "http://www./" EMBED Equation.3 是的最小值;
(Ⅲ)对满足(Ⅱ)的条件的一个实数对 HYPERLINK "http://www./" EMBED Equation.3 ,试构造一个定义在,且 HYPERLINK "http://www./" EMBED Equation.3 上的函数,使当 HYPERLINK "http://www./" EMBED Equation.3 时,,当 HYPERLINK "http://www./" EMBED Equation.3 时,取得最大值的自变量的值构成以 HYPERLINK "http://www./" EMBED Equation.3 为首项的等差数列。
21、(本小题满分14分)
椭圆过点P,且离心率为,F为椭圆的右焦点,、两点在椭圆上,且 ,定点(-4,0).
(Ⅰ)求椭圆C的方程;
(Ⅱ)当时 ,问:MN与AF是否垂直;
并证明你的结论.
(Ⅲ)当、两点在上运动,
且 =6时,
求直线MN的方程.
22、(本小题满分15分)
已知函数在上为增函数,且,为常数,.
(Ⅰ)求的值;
(Ⅱ)若在上为单调函数,求m的取值范围;
(Ⅲ)设,若在上至少存在一个,使得成立,求的m取值范围.
2011年台州市四校联考数学(理科)答案
一、选择题(每小题5分,共50分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A D C B D A C D D B
二、填空题(每小题4分,共28分)
11. 12. (13,49) 13. 14.
15. 16. 9 17.
三、解答题(共72分)
(18)(本题满分l4分)
解:(Ⅰ)当 …………………6分
(Ⅱ)时, ;时,
①当时,要使必须
②当时,,所以使的不存在,
③,要使,必须
综上可知,使的实数的范围为 ……………………14分
(19)(本题满分l4分)
(Ⅰ),
由,得………………2分
由及,得………………4分
…………6分
(Ⅱ).………………8分
为三角形内角,所以………………10分
,,…………14分
(20)(本题满分14分)
解:(Ⅰ)当时, HYPERLINK "http://www./" EMBED Equation.3 ,
若, HYPERLINK "http://www./" EMBED Equation.3 ,则在 HYPERLINK "http://www./" EMBED Equation.3 上单调递减,不符题意。
故,要使 HYPERLINK "http://www./" EMBED Equation.3 在上单调递增,必须满足 HYPERLINK "http://www./" EMBED Equation.3 ,∴ 。 (4分)
(Ⅱ)若 HYPERLINK "http://www./" EMBED Equation.3 ,,则 HYPERLINK "http://www./" EMBED Equation.3 无最大值,故,∴ HYPERLINK "http://www./" EMBED Equation.3 为二次函数,
要使有最大值,必须满足 HYPERLINK "http://www./" EMBED Equation.3 ,即且 HYPERLINK "http://www./" EMBED Equation.3 ,
此时,时, HYPERLINK "http://www./" EMBED Equation.3 有最大值。
又取最小值时, HYPERLINK "http://www./" EMBED Equation.3 ,依题意,有,则 HYPERLINK "http://www./" EMBED Equation.3 ,
∵且 HYPERLINK "http://www./" EMBED Equation.3 ,∴,得 HYPERLINK "http://www./" EMBED Equation.3 ,此时或 HYPERLINK "http://www./" EMBED Equation.3 。
∴满足条件的实数对是 HYPERLINK "http://www./" EMBED Equation.3 。 (9分)
(Ⅲ)当实数对是 HYPERLINK "http://www./" EMBED Equation.3 时, (14分)
依题意,只需构造以2(或2的正整数倍)为周期的周期函数即可。
如对 HYPERLINK "http://www./" EMBED Equation.3 ,,
此时, HYPERLINK "http://www./" EMBED Equation.3 ,
故
21,解:(Ⅰ)椭圆的离心率为
即可得 --2分
又椭圆过点P
解得,,椭圆C的方程为----- -----------4分
(Ⅱ)设,
则,
当时,, -----------5分
由M,N两点在椭圆上,
---------6分
若,则(舍去), ------------7分
. ------------8分
(Ⅲ)因为=6.--9分
由已知点F(2,0), 所以|AF|=6, 即得|yM-yN|= ------------10分
当MN轴时,故直线的斜率存在. ------------11分
不妨设直线MN的方程为:-----
联立、得 ------------12分
||=解得 ------------14分
此时,直线MN的方程为或 ------------15分
(22)(本题满分15分)
解:(1)由题意:在上恒成立,即,
在上恒成立,
只需sin…………(4分)
(2) 由(1),得f(x)-g(x)=mx-,,由于f(x)-g(x)在其定义域内为单调函数,则在上恒成立,即在上恒成立,故,综上,m的取值范围是 …………(9分)
(3)构造函数F(x)=f(x)-g(x)-h(x),,
当由得,,所以在上不存在一个,使得; …………(12分)
当m>0时,,因为,所以在上恒成立,故F(x)在上单调递增,,故m的取值范围是…………………………………………………………………………(15分)
另法:(3) 令
第21题
第21题
同课章节目录
