4.3.1 中心对称同步练习(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第四章 图形的平移与旋转
3 中心对称
第1课时
考点突破
考点1 中心对称的概念与性质
例1 如图,将一张直角三角形纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′的位置,则四边形ACE′E是什么图形?为什么?
思路导引: 根据对称中心的概念,把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称根据题意可得△BDE和△BDE′关于点D中心对称,这是解题的关键所在.
方法归纳
1.中心对称和轴对称的对比:
中心对称 轴对称
有一个对称中心 有一条对称轴
图形绕中心旋转180° 图形沿轴折叠
旋转后和另一图形重合 折叠后和另一图形重合
2.中心对称性质的“两个对应”:①对应边相等、平行或在同一条直线上;②对应角相等。
题组训练
1.下列描述中心对称的特征语句中正确的是( )
A.连接对称点的线段不一定经过对称中心
B.对称中心不一定平分连接对称点的线段
C.连接对称点的线段一定经过对称中心,但不一定被对称中心平分
D.连接对称点的线段一定经过对称中心,且被对称中心平分
2.如图,△AOB与△COD成中心对称,连接AD,BC,则AD与BC的关系是__________。
3.如图所示,如果甲、乙关于点O成中心对称,那么乙图中不符合题意的一块是( )
4.小明、小辉两家所在位置关于学校中心对称.如果小明家距学校2 km,那么他们两家相距 ___________ km.
5.如图所示,在△ABC中,点D,E分别是AB,AC边的中点,若把△ADE绕着点E按顺时针方向旋转180°得到△CFE,则CF与BD的数量与位置关系是______________。
考点2 画一个图形关于已知点的对称图形
例2 如图,已知四边形ABCD和图形外一点O,作出四边形ABCD关于点O成中心对称的图形.
思路导引: 连接AO,并延长至点A′,使OA=OA′;同理可作出其他各点的对应点,顺次连接各对应点即可。
方法归纳
画一个图形关于某一点的对称图形的三个步骤:
(1)在原图形上确定关键点;
(2)分别画出关键点的对称点;
(3)按照图形的连接顺序连接关键点的对称点。
题组训练
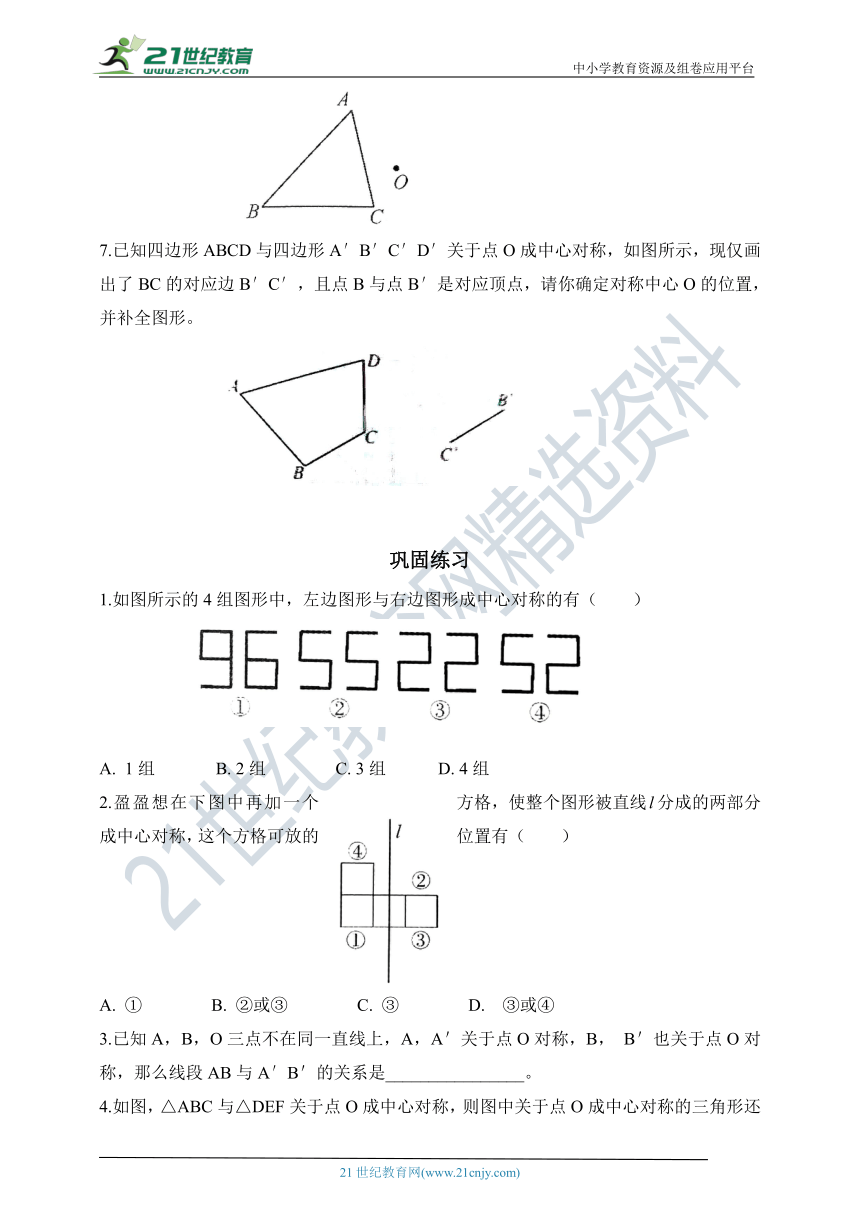
6,如图,已知△ABC,作出与它关于点O对称的图形。
7.已知四边形ABCD与四边形A′B′C′D′关于点O成中心对称,如图所示,现仅画出了BC的对应边B′C′,且点B与点B′是对应顶点,请你确定对称中心O的位置,并补全图形。
巩固练习
1.如图所示的4组图形中,左边图形与右边图形成中心对称的有( )
1组 B. 2组 C. 3组 D. 4组
2.盈盈想在下图中再加一个方格,使整个图形被直线分成的两部分成中心对称,这个方格可放的位置有( )
① B. ②或③ C. ③ D. ③或④
3.已知A,B,O三点不在同一直线上,A,A'关于点O对称,B, B'也关于点O对称,那么线段AB与A′B'的关系是________________。
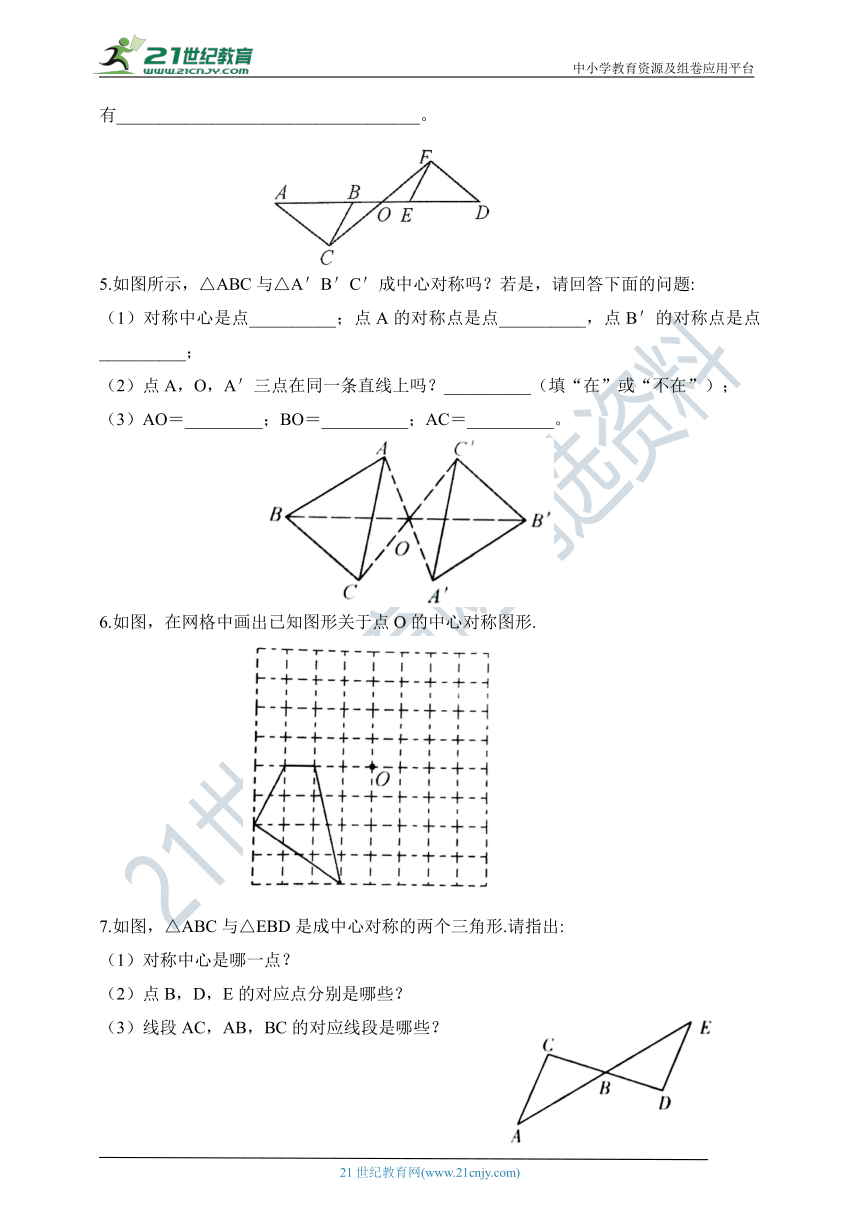
4.如图,△ABC与△DEF关于点O成中心对称,则图中关于点O成中心对称的三角形还有___________________________________。
5.如图所示,△ABC与△A'B'C'成中心对称吗?若是,请回答下面的问题:
(1)对称中心是点__________;点A的对称点是点__________,点B'的对称点是点__________;
(2)点A,O,A'三点在同一条直线上吗?__________(填“在”或“不在”);
(3)AO=_________;BO=__________;AC=__________。
6.如图,在网格中画出已知图形关于点O的中心对称图形.
7.如图,△ABC与△EBD是成中心对称的两个三角形.请指出:
(1)对称中心是哪一点?
(2)点B,D,E的对应点分别是哪些?
(3)线段AC,AB,BC的对应线段是哪些?
8.(曲靖)如图,在数轴上,A1,P两点表示的数分别是1,2,A1,A2关于点O对称,A2,A3关于点P对称,A3,A4关于点O对称,A4,A5关于点P对称…依此规律,则点A14表示的数是____________。
9.两次翻折(对称轴互相垂直)后的图形与原图形关于____________成___________对称。
10.如图,每个小方格都是边长为1的小正方形,△ABC的顶点均在格点上,请按要求画图与作答。
(1)把△ABC绕点P旋转180°得△A′B′C′;
(2)把△ABC向右平移7个单位得△A″B″C″;
(3)△A′B′C′与△A″B″C″是否成中心对称,若是,找出对称中心P′。
11.如图是一个6×6的棋盘,两人各持若干张1×2的卡片轮流在棋盘上盖卡片,每人每次用一张卡片盖住相邻的两个空格,谁找不出相邻的两个空格放卡片就算谁输,你有什么办法能战胜对手呢?
参考答案
考点突破
例1 解:四边形ACE'E是平行四边形,理由:∵DE是△ABC的中位线,∴ DE// AC, DE= AC.由△BDE绕着CB的中点D逆时针旋转180?得到△CDE′,可得DE'=DE,于是可得E'E=AC. ∵DE// AC, E'E=AC,∴四边形ACE'E是平行四边形。
题组训练
D 2. 平行且相等 3,C 4. 4 5. CF= BD,CF// BD
例2 解:如图,连接AO并延长至A',使A'O=AO,得点A对称点A',同理,可得点B, C,D的对称点B',C', D',顺次连接四点得四边形A'B'C'D',即为所要求作的四边形ABCD关于点O成中心对称的图形.
题组训练
6,解:如图所示,连接AO并延长至点D,使OD=OA,同样作出E,F两点;
分别连接DE, EF, FD, △DEF就是△ABC关于点O对称的图形.
7,解:分别连接BB',CC′,其交点即为对称中心O,连接AO并延长到点A',使
OA'=OA,得点A的对称点A′.同理,作出点D的对称点D',依次连接A′B',C′D',A′D',即得四边形A'B'C′D'(图略).
巩固练习
C 2. C 3,平行且相等
4. △BOC与△EOF,△AOC与△DOF
5. (1)O A′ B (2)在 (3)A'O B′O A'C′
6,解:如图所示.
7.解: (1)点B. (2)B与B,D与C,E与A.
(3)AC与ED,AB与EB,BC与BD.
8,-25
9,两条对称轴的交点 中心
10,解:(1)△A'B'C'如图所示.
(2)△A"B"C"如图所示.
(3)△A'B'C'与△A"B"C"成中心对称,对称中心P'如图所示.
11.解:让对手先盖卡片,然后自己盖住对手所盖空格关于6×6棋盘的中心对称的空格,这样只要对手能用卡片盖住相邻的两个空格,自己也能找到其中心对称的空格用卡片盖住,因此,最先找不出相邻两个空格的是对手,自己稳操胜券。
_21?????????è?????(www.21cnjy.com)_
第四章 图形的平移与旋转
3 中心对称
第1课时
考点突破
考点1 中心对称的概念与性质
例1 如图,将一张直角三角形纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′的位置,则四边形ACE′E是什么图形?为什么?
思路导引: 根据对称中心的概念,把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称根据题意可得△BDE和△BDE′关于点D中心对称,这是解题的关键所在.
方法归纳
1.中心对称和轴对称的对比:
中心对称 轴对称
有一个对称中心 有一条对称轴
图形绕中心旋转180° 图形沿轴折叠
旋转后和另一图形重合 折叠后和另一图形重合
2.中心对称性质的“两个对应”:①对应边相等、平行或在同一条直线上;②对应角相等。
题组训练
1.下列描述中心对称的特征语句中正确的是( )
A.连接对称点的线段不一定经过对称中心
B.对称中心不一定平分连接对称点的线段
C.连接对称点的线段一定经过对称中心,但不一定被对称中心平分
D.连接对称点的线段一定经过对称中心,且被对称中心平分
2.如图,△AOB与△COD成中心对称,连接AD,BC,则AD与BC的关系是__________。
3.如图所示,如果甲、乙关于点O成中心对称,那么乙图中不符合题意的一块是( )
4.小明、小辉两家所在位置关于学校中心对称.如果小明家距学校2 km,那么他们两家相距 ___________ km.
5.如图所示,在△ABC中,点D,E分别是AB,AC边的中点,若把△ADE绕着点E按顺时针方向旋转180°得到△CFE,则CF与BD的数量与位置关系是______________。
考点2 画一个图形关于已知点的对称图形
例2 如图,已知四边形ABCD和图形外一点O,作出四边形ABCD关于点O成中心对称的图形.
思路导引: 连接AO,并延长至点A′,使OA=OA′;同理可作出其他各点的对应点,顺次连接各对应点即可。
方法归纳
画一个图形关于某一点的对称图形的三个步骤:
(1)在原图形上确定关键点;
(2)分别画出关键点的对称点;
(3)按照图形的连接顺序连接关键点的对称点。
题组训练
6,如图,已知△ABC,作出与它关于点O对称的图形。
7.已知四边形ABCD与四边形A′B′C′D′关于点O成中心对称,如图所示,现仅画出了BC的对应边B′C′,且点B与点B′是对应顶点,请你确定对称中心O的位置,并补全图形。
巩固练习
1.如图所示的4组图形中,左边图形与右边图形成中心对称的有( )
1组 B. 2组 C. 3组 D. 4组
2.盈盈想在下图中再加一个方格,使整个图形被直线分成的两部分成中心对称,这个方格可放的位置有( )
① B. ②或③ C. ③ D. ③或④
3.已知A,B,O三点不在同一直线上,A,A'关于点O对称,B, B'也关于点O对称,那么线段AB与A′B'的关系是________________。
4.如图,△ABC与△DEF关于点O成中心对称,则图中关于点O成中心对称的三角形还有___________________________________。
5.如图所示,△ABC与△A'B'C'成中心对称吗?若是,请回答下面的问题:
(1)对称中心是点__________;点A的对称点是点__________,点B'的对称点是点__________;
(2)点A,O,A'三点在同一条直线上吗?__________(填“在”或“不在”);
(3)AO=_________;BO=__________;AC=__________。
6.如图,在网格中画出已知图形关于点O的中心对称图形.
7.如图,△ABC与△EBD是成中心对称的两个三角形.请指出:
(1)对称中心是哪一点?
(2)点B,D,E的对应点分别是哪些?
(3)线段AC,AB,BC的对应线段是哪些?
8.(曲靖)如图,在数轴上,A1,P两点表示的数分别是1,2,A1,A2关于点O对称,A2,A3关于点P对称,A3,A4关于点O对称,A4,A5关于点P对称…依此规律,则点A14表示的数是____________。
9.两次翻折(对称轴互相垂直)后的图形与原图形关于____________成___________对称。
10.如图,每个小方格都是边长为1的小正方形,△ABC的顶点均在格点上,请按要求画图与作答。
(1)把△ABC绕点P旋转180°得△A′B′C′;
(2)把△ABC向右平移7个单位得△A″B″C″;
(3)△A′B′C′与△A″B″C″是否成中心对称,若是,找出对称中心P′。
11.如图是一个6×6的棋盘,两人各持若干张1×2的卡片轮流在棋盘上盖卡片,每人每次用一张卡片盖住相邻的两个空格,谁找不出相邻的两个空格放卡片就算谁输,你有什么办法能战胜对手呢?
参考答案
考点突破
例1 解:四边形ACE'E是平行四边形,理由:∵DE是△ABC的中位线,∴ DE// AC, DE= AC.由△BDE绕着CB的中点D逆时针旋转180?得到△CDE′,可得DE'=DE,于是可得E'E=AC. ∵DE// AC, E'E=AC,∴四边形ACE'E是平行四边形。
题组训练
D 2. 平行且相等 3,C 4. 4 5. CF= BD,CF// BD
例2 解:如图,连接AO并延长至A',使A'O=AO,得点A对称点A',同理,可得点B, C,D的对称点B',C', D',顺次连接四点得四边形A'B'C'D',即为所要求作的四边形ABCD关于点O成中心对称的图形.
题组训练
6,解:如图所示,连接AO并延长至点D,使OD=OA,同样作出E,F两点;
分别连接DE, EF, FD, △DEF就是△ABC关于点O对称的图形.
7,解:分别连接BB',CC′,其交点即为对称中心O,连接AO并延长到点A',使
OA'=OA,得点A的对称点A′.同理,作出点D的对称点D',依次连接A′B',C′D',A′D',即得四边形A'B'C′D'(图略).
巩固练习
C 2. C 3,平行且相等
4. △BOC与△EOF,△AOC与△DOF
5. (1)O A′ B (2)在 (3)A'O B′O A'C′
6,解:如图所示.
7.解: (1)点B. (2)B与B,D与C,E与A.
(3)AC与ED,AB与EB,BC与BD.
8,-25
9,两条对称轴的交点 中心
10,解:(1)△A'B'C'如图所示.
(2)△A"B"C"如图所示.
(3)△A'B'C'与△A"B"C"成中心对称,对称中心P'如图所示.
11.解:让对手先盖卡片,然后自己盖住对手所盖空格关于6×6棋盘的中心对称的空格,这样只要对手能用卡片盖住相邻的两个空格,自己也能找到其中心对称的空格用卡片盖住,因此,最先找不出相邻两个空格的是对手,自己稳操胜券。
_21?????????è?????(www.21cnjy.com)_
