浙江省杭州市杭二高2020-2021学年高一上学期期中考试数学试题 Word版含答案
文档属性
| 名称 | 浙江省杭州市杭二高2020-2021学年高一上学期期中考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 424.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 18:19:09 | ||
图片预览




文档简介
2020学年杭二高一上期中
一、选择题:每小题4分,共40分.
1.已知集合A={a,b},B={a+1,3}(a,b∈R),若A∩B={2},则A∪B=
A.{2} B.{3} C.{1,2,3} D.{0,1,2}
2.与函数false表示同一函数是
A.false B.false C.false D.false
3.已知幂函数false的图像过点(9,3),若f(t)=2,则实数t的值为
A.false B.false C.false D.4
4.己知函数false,x∈R,且false,false,false,false,…,false,n∈N*,则函数false的解析式可以是
A.false B.false C.false D.false
5.设函数false,则false,则a=
A.0 B.false C.false D.1
6.若false,则
A.false B.false C.false D.false
7.已知false,false,则
A.false B.false C.false D.false
8.若对任意使得关于x的方程false(ac≠0)有实数解的a,b,c均有false
false,则实数r的最大值是
A.1 B.false C.false D.2
9.【多选题】命题“false,false”是真命题的一个充分不必要条件是
A.false B.false c.false D.false
10.【多选题】《几何原木》中的几何代数法是以几何方法研究代数问题,这种方法是后西方数学家处理问题的重要依据,通过这一原理,很多的代数公理或定理都能够通过图形实现证明,也称之为无字证明,现有图形如图所示,C为线段AB上的点,且AC=a,BC=b,O为AB的中点,以AB为直径作半圆,过点C作AB的线交半圆于D,连结OD,AD,BD,过点C作OD的垂线,垂足为E,则该图形可以完成的所有的无字证明为
245935527305A.false(a>0,b>0) B.false(a>0,b>0)
C.false(a>0,b>0) D.false(a>0,b>0)
二、填空题:单空题每题4分,多空题每题6分.
11.华为5G通信编码的极化码技术方案基于矩阵的乘法,如:false,其中false,false,已知定义在R上不恒为О的函数false,对任意a,b∈R有:
false,且满足false,则
A.false B.false C.false是偶函数 D.false是奇函数
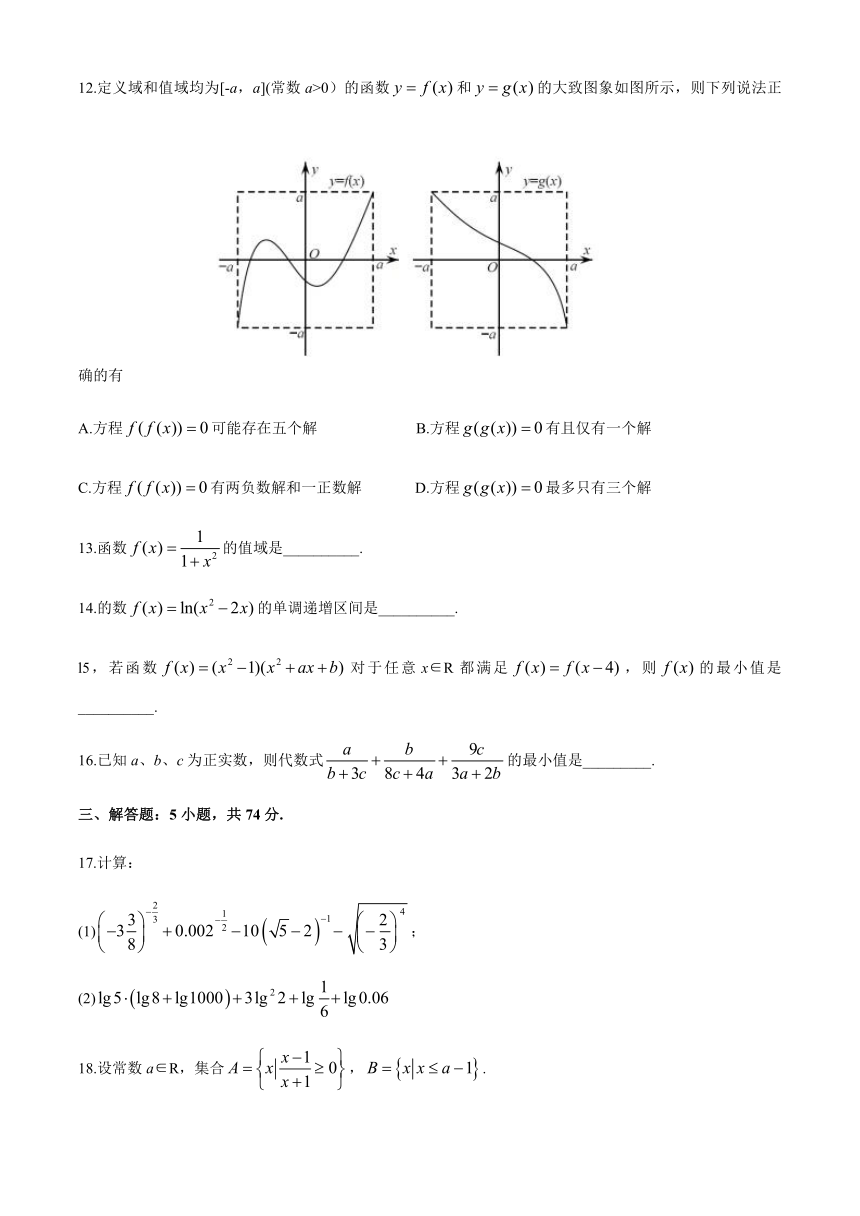
114617579883012.定义域和值域均为[-a,a](常数a>0)的函数false和false的大致图象如图所示,则下列说法正确的有
A.方程false可能存在五个解 B.方程false有且仅有一个解
C.方程false有两负数解和一正数解 D.方程false最多只有三个解
13.函数false的值域是__________.
14.的数false的单调递增区间是__________.
l5,若函数false对于任意x∈R都满足false,则false的最小值是__________.
16.已知a、b、c为正实数,则代数式false的最小值是_________.
三、解答题:5小题,共74分.
17.计算:
(1)false;
(2)false
18.设常数a∈R,集合false,false.
(1)若a=2,求A∩B,A∩(?RB);
(2)若A∪B=R,求a的取值范围.
19.2020年是不平凡的一年,经历过短暂的网课学习后,同学们回到校园开始了正常的学习生活,为了提高学生的学习效率,某心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其注意力指数p与听课时间t之间的关系满足如图所示的曲线,当t∈(0,14]时,曲线是二次函数图象的一部分,当t∈(14,40]时,曲线是函数false,a>0且a≠l图象的一部分,根据专家研究,当注意力指数p大于等于80时听课效果最佳.
(1)试求p=f(t)的函数关系式;
(2)一道数学难题,讲解需要22分钟,问老师能否经过合理安排在学生听课效果最佳时讲解完?请说明理由.
35001202730520.已知函数false(a>0,a≠1).
(1)若a>l,不等式false在x∈R上恒成立,求实致b的取值范围;
(2)若false且false在[1,+∞)上的最小值为-2,求m的值.
21.已知函数false为奇函数.
(1)求实数上的值;
(2)判断并证明函数false的单调性;
(3)若在false,false∈(1,+oo),使得函数false在区间[false,false]上的值域false,求实数m的取值范围.
22.设函数false,a,b∈R.
(1)若函数false在[0,2]上单调递增,在(2,+∞)单调递减,求实数a的值;
(2)若对任意的实数b∈[0,1]及任意的x∈[-3,3],不等式false恒成立,求实数a的取值范围.
2020学年杭二高一上期中
一、选择题:每小题4分,共40分.
1.已知集合A={a,b},B={a+1,3}(a,b∈R),若A∩B={2},则A∪B=
A.{2} B.{3} C.{1,2,3} D.{0,1,2}
选:C.
2.与函数false表示同一函数是
A.false B.false C.false D.false
选:D.
3.已知幂函数false的图像过点(9,3),若f(t)=2,则实数t的值为
A.false B.false C.false D.4
选:D.
4.己知函数false,x∈R,且false,false,false,false,…,false,n∈N*,则函数false的解析式可以是
A.false B.false C.false D.false
选:A.
5.设函数false,则false,则a=
A.0 B.false C.false D.1
选:C.
6.若false,则
A.false B.false C.false D.false
选:D.
7.已知false,false,则
A.false B.false C.false D.false
选:B.
8.若对任意使得关于x的方程false(ac≠0)有实数解的a,b,c均有false
false,则实数r的最大值是
A.1 B.false C.false D.2
选:B.
9.【多选题】命题“false,false”是真命题的一个充分不必要条件是
A.false B.false c.false D.false
选:CD.
10.【多选题】《几何原木》中的几何代数法是以几何方法研究代数问题,这种方法是后西方数学家处理问题的重要依据,通过这一原理,很多的代数公理或定理都能够通过图形实现证明,也称之为无字证明,现有图形如图所示,C为线段AB上的点,且AC=a,BC=b,O为AB的中点,以AB为直径作半圆,过点C作AB的线交半圆于D,连结OD,AD,BD,过点C作OD的垂线,垂足为E,则该图形可以完成的所有的无字证明为
245935527305A.false(a>0,b>0) B.false(a>0,b>0)
C.false(a>0,b>0) D.false(a>0,b>0)
选:AC.
二、填空题:单空题每题4分,多空题每题6分.
11.华为5G通信编码的极化码技术方案基于矩阵的乘法,如:false,其中false,false,已知定义在R上不恒为О的函数false,对任意a,b∈R有:
false,且满足false,则
A.false B.false C.false是偶函数 D.false是奇函数
选:AC.
12.定义域和值域均为[-a,a](常数a>0)的函数false和false的大致图象如图所示,则下列说法正确的有
127317524765A.方程false可能存在五个解 B.方程false有且仅有一个解
C.方程false有两负数解和一正数解 D.方程false最多只有三个解
选:ABC.
13.函数false的值域是__________.
【答案】值域(0,1]
14.的数false的单调递增区间是__________.
【答案】(2,+∞)
l5,若函数false对于任意x∈R都满足false,则false的最小值是__________.
【答案】9.
16.已知a、b、c为正实数,则代数式false的最小值是_________.
【答案】false.
三、解答题:5小题,共74分.
17.计算:
(1)false;
(2)false
解:(1)原式=false
false
(2)原式=false
=false
18.设常数a∈R,集合false,false.
(1)若a=2,求A∩B,A∩(?RB);
(2)若A∪B=R,求a的取值范围.
解:(1)∵a=2,
∴false,false,false,
∴false,false
(2)1′当-a<1即a>-1时,false,
∴false
∴false
2′当-a>l即a<-l时,false,
∴false,无解
3′当-a=1即a=—1时,false
∴false,无解
综上所述,a的取值范围为false.
19.2020年是不平凡的一年,经历过短暂的网课学习后,同学们回到校园开始了正常的学习生活,为了提高学生的学习效率,某心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其注意力指数p与听课时间t之间的关系满足如图所示的曲线,当t∈(0,14]时,曲线是二次函数图象的一部分,当t∈(14,40]时,曲线是函数false,a>0且a≠l图象的一部分,根据专家研究,当注意力指数p大于等于80时听课效果最佳.
(1)试求p=f(t)的函数关系式;
(2)一道数学难题,讲解需要22分钟,问老师能否经过合理安排在学生听课效果最佳时讲解完?请说明理由.
3183255-116840解:(1)当t∈(0,14]时,设false,代入(14,81)得false,
∴false
当t∈(14,40]时,代入(14,81)得false,
∴false
∴false
(2)令false,当t∈(0,14]时,false,得false
当t∈(14,40]时,false,得14∴false的解集为{t|12-2false≤t≤32},
∴听课效果最佳时间段为32-(12-2false)=20+2false>22,
∴师能经过合理安排在学生听课效果最佳时讲完
20.已知函数false(a>0,a≠1).
(1)若a>l,不等式false在x∈R上恒成立,求实致b的取值范围;
(2)若false且false在[1,+∞)上的最小值为-2,求m的值.
解:(1)false,false,即false是x∈R上的奇函数.
且a>l时,false且单调递增,false(x>0)也单调递增,
由复合函数单调性可知false在x∈R上单调递增.
原不等式false,
因此,false对x∈R恒成立,
故false,即false.
(2)∵false,且a>0,
∴a=2(a=-false<0舍去).
因此,false
当x∈[1,+∞)时,false,令false,,其中x∈[1,+∞),
并令false,其中false,二次函数对称轴false
①若false,则false,解得false,矛盾,故无解;
②若false,则false,解得m=-2(m=-2综上所述,本题所求m=2.
21.已知函数false为奇函数.
(1)求实数上的值;
(2)判断并证明函数false的单调性;
(3)若在false,false∈(1,+oo),使得函数false在区间[false,false]上的值域false,求实数m的取值范围.
解:(1)由题false,所以false
即false,当k=-1时,false,舍。所以k=1.
(2)由题false,定义域为(-∞,-1)∪(1,+∞),
所以false的增区间是:(-∞,-1)和(1,+∞)
依题意设false,所以false
因为false,所以false,false
又因为false,
所以false
所以false,即false
所以函数false在(1,+∞)上单调递增.
1308735687705(3)函数false的图象如图所示:
原命题等价于false在x∈(1,+∞)上有两个不同实数解
即false在x∈(1,+∞)上有两个不同实数解
所以false上x∈(1,+∞)有两个不同实数解
设t=x-1∈(1,+∞),即false.在t∈(1,+∞)上有两有两个不同解
所以false,即false.
22.设函数false,a,b∈R.
(1)若函数false在[0,2]上单调递增,在(2,+∞)单调递减,求实数a的值;
(2)若对任意的实数b∈[0,1]及任意的x∈[-3,3],不等式false恒成立,求实数a的取值范围.
解:(1)false,显然a<0,则false解得false,经检验,符合题意,
∴a的值为false.
不等式false恒成立,即-2≤f(x)≤2,令false,
则false恒成立,则-2≤g(x)≤1恒成立.
则由false解得false
false可化为false恒成立,
先考虑false恒成立,即false,
由false恒成立知,false恒成立,则false,false.
只需证明:false
右边:false
左边:当false时,false,
当false时,false,证毕!
一、选择题:每小题4分,共40分.
1.已知集合A={a,b},B={a+1,3}(a,b∈R),若A∩B={2},则A∪B=
A.{2} B.{3} C.{1,2,3} D.{0,1,2}
2.与函数false表示同一函数是
A.false B.false C.false D.false
3.已知幂函数false的图像过点(9,3),若f(t)=2,则实数t的值为
A.false B.false C.false D.4
4.己知函数false,x∈R,且false,false,false,false,…,false,n∈N*,则函数false的解析式可以是
A.false B.false C.false D.false
5.设函数false,则false,则a=
A.0 B.false C.false D.1
6.若false,则
A.false B.false C.false D.false
7.已知false,false,则
A.false B.false C.false D.false
8.若对任意使得关于x的方程false(ac≠0)有实数解的a,b,c均有false
false,则实数r的最大值是
A.1 B.false C.false D.2
9.【多选题】命题“false,false”是真命题的一个充分不必要条件是
A.false B.false c.false D.false
10.【多选题】《几何原木》中的几何代数法是以几何方法研究代数问题,这种方法是后西方数学家处理问题的重要依据,通过这一原理,很多的代数公理或定理都能够通过图形实现证明,也称之为无字证明,现有图形如图所示,C为线段AB上的点,且AC=a,BC=b,O为AB的中点,以AB为直径作半圆,过点C作AB的线交半圆于D,连结OD,AD,BD,过点C作OD的垂线,垂足为E,则该图形可以完成的所有的无字证明为
245935527305A.false(a>0,b>0) B.false(a>0,b>0)
C.false(a>0,b>0) D.false(a>0,b>0)
二、填空题:单空题每题4分,多空题每题6分.
11.华为5G通信编码的极化码技术方案基于矩阵的乘法,如:false,其中false,false,已知定义在R上不恒为О的函数false,对任意a,b∈R有:
false,且满足false,则
A.false B.false C.false是偶函数 D.false是奇函数
114617579883012.定义域和值域均为[-a,a](常数a>0)的函数false和false的大致图象如图所示,则下列说法正确的有
A.方程false可能存在五个解 B.方程false有且仅有一个解
C.方程false有两负数解和一正数解 D.方程false最多只有三个解
13.函数false的值域是__________.
14.的数false的单调递增区间是__________.
l5,若函数false对于任意x∈R都满足false,则false的最小值是__________.
16.已知a、b、c为正实数,则代数式false的最小值是_________.
三、解答题:5小题,共74分.
17.计算:
(1)false;
(2)false
18.设常数a∈R,集合false,false.
(1)若a=2,求A∩B,A∩(?RB);
(2)若A∪B=R,求a的取值范围.
19.2020年是不平凡的一年,经历过短暂的网课学习后,同学们回到校园开始了正常的学习生活,为了提高学生的学习效率,某心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其注意力指数p与听课时间t之间的关系满足如图所示的曲线,当t∈(0,14]时,曲线是二次函数图象的一部分,当t∈(14,40]时,曲线是函数false,a>0且a≠l图象的一部分,根据专家研究,当注意力指数p大于等于80时听课效果最佳.
(1)试求p=f(t)的函数关系式;
(2)一道数学难题,讲解需要22分钟,问老师能否经过合理安排在学生听课效果最佳时讲解完?请说明理由.
35001202730520.已知函数false(a>0,a≠1).
(1)若a>l,不等式false在x∈R上恒成立,求实致b的取值范围;
(2)若false且false在[1,+∞)上的最小值为-2,求m的值.
21.已知函数false为奇函数.
(1)求实数上的值;
(2)判断并证明函数false的单调性;
(3)若在false,false∈(1,+oo),使得函数false在区间[false,false]上的值域false,求实数m的取值范围.
22.设函数false,a,b∈R.
(1)若函数false在[0,2]上单调递增,在(2,+∞)单调递减,求实数a的值;
(2)若对任意的实数b∈[0,1]及任意的x∈[-3,3],不等式false恒成立,求实数a的取值范围.
2020学年杭二高一上期中
一、选择题:每小题4分,共40分.
1.已知集合A={a,b},B={a+1,3}(a,b∈R),若A∩B={2},则A∪B=
A.{2} B.{3} C.{1,2,3} D.{0,1,2}
选:C.
2.与函数false表示同一函数是
A.false B.false C.false D.false
选:D.
3.已知幂函数false的图像过点(9,3),若f(t)=2,则实数t的值为
A.false B.false C.false D.4
选:D.
4.己知函数false,x∈R,且false,false,false,false,…,false,n∈N*,则函数false的解析式可以是
A.false B.false C.false D.false
选:A.
5.设函数false,则false,则a=
A.0 B.false C.false D.1
选:C.
6.若false,则
A.false B.false C.false D.false
选:D.
7.已知false,false,则
A.false B.false C.false D.false
选:B.
8.若对任意使得关于x的方程false(ac≠0)有实数解的a,b,c均有false
false,则实数r的最大值是
A.1 B.false C.false D.2
选:B.
9.【多选题】命题“false,false”是真命题的一个充分不必要条件是
A.false B.false c.false D.false
选:CD.
10.【多选题】《几何原木》中的几何代数法是以几何方法研究代数问题,这种方法是后西方数学家处理问题的重要依据,通过这一原理,很多的代数公理或定理都能够通过图形实现证明,也称之为无字证明,现有图形如图所示,C为线段AB上的点,且AC=a,BC=b,O为AB的中点,以AB为直径作半圆,过点C作AB的线交半圆于D,连结OD,AD,BD,过点C作OD的垂线,垂足为E,则该图形可以完成的所有的无字证明为
245935527305A.false(a>0,b>0) B.false(a>0,b>0)
C.false(a>0,b>0) D.false(a>0,b>0)
选:AC.
二、填空题:单空题每题4分,多空题每题6分.
11.华为5G通信编码的极化码技术方案基于矩阵的乘法,如:false,其中false,false,已知定义在R上不恒为О的函数false,对任意a,b∈R有:
false,且满足false,则
A.false B.false C.false是偶函数 D.false是奇函数
选:AC.
12.定义域和值域均为[-a,a](常数a>0)的函数false和false的大致图象如图所示,则下列说法正确的有
127317524765A.方程false可能存在五个解 B.方程false有且仅有一个解
C.方程false有两负数解和一正数解 D.方程false最多只有三个解
选:ABC.
13.函数false的值域是__________.
【答案】值域(0,1]
14.的数false的单调递增区间是__________.
【答案】(2,+∞)
l5,若函数false对于任意x∈R都满足false,则false的最小值是__________.
【答案】9.
16.已知a、b、c为正实数,则代数式false的最小值是_________.
【答案】false.
三、解答题:5小题,共74分.
17.计算:
(1)false;
(2)false
解:(1)原式=false
false
(2)原式=false
=false
18.设常数a∈R,集合false,false.
(1)若a=2,求A∩B,A∩(?RB);
(2)若A∪B=R,求a的取值范围.
解:(1)∵a=2,
∴false,false,false,
∴false,false
(2)1′当-a<1即a>-1时,false,
∴false
∴false
2′当-a>l即a<-l时,false,
∴false,无解
3′当-a=1即a=—1时,false
∴false,无解
综上所述,a的取值范围为false.
19.2020年是不平凡的一年,经历过短暂的网课学习后,同学们回到校园开始了正常的学习生活,为了提高学生的学习效率,某心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其注意力指数p与听课时间t之间的关系满足如图所示的曲线,当t∈(0,14]时,曲线是二次函数图象的一部分,当t∈(14,40]时,曲线是函数false,a>0且a≠l图象的一部分,根据专家研究,当注意力指数p大于等于80时听课效果最佳.
(1)试求p=f(t)的函数关系式;
(2)一道数学难题,讲解需要22分钟,问老师能否经过合理安排在学生听课效果最佳时讲解完?请说明理由.
3183255-116840解:(1)当t∈(0,14]时,设false,代入(14,81)得false,
∴false
当t∈(14,40]时,代入(14,81)得false,
∴false
∴false
(2)令false,当t∈(0,14]时,false,得false
当t∈(14,40]时,false,得14
∴听课效果最佳时间段为32-(12-2false)=20+2false>22,
∴师能经过合理安排在学生听课效果最佳时讲完
20.已知函数false(a>0,a≠1).
(1)若a>l,不等式false在x∈R上恒成立,求实致b的取值范围;
(2)若false且false在[1,+∞)上的最小值为-2,求m的值.
解:(1)false,false,即false是x∈R上的奇函数.
且a>l时,false且单调递增,false(x>0)也单调递增,
由复合函数单调性可知false在x∈R上单调递增.
原不等式false,
因此,false对x∈R恒成立,
故false,即false.
(2)∵false,且a>0,
∴a=2(a=-false<0舍去).
因此,false
当x∈[1,+∞)时,false,令false,,其中x∈[1,+∞),
并令false,其中false,二次函数对称轴false
①若false,则false,解得false,矛盾,故无解;
②若false,则false,解得m=-2(m=-2
21.已知函数false为奇函数.
(1)求实数上的值;
(2)判断并证明函数false的单调性;
(3)若在false,false∈(1,+oo),使得函数false在区间[false,false]上的值域false,求实数m的取值范围.
解:(1)由题false,所以false
即false,当k=-1时,false,舍。所以k=1.
(2)由题false,定义域为(-∞,-1)∪(1,+∞),
所以false的增区间是:(-∞,-1)和(1,+∞)
依题意设false,所以false
因为false,所以false,false
又因为false,
所以false
所以false,即false
所以函数false在(1,+∞)上单调递增.
1308735687705(3)函数false的图象如图所示:
原命题等价于false在x∈(1,+∞)上有两个不同实数解
即false在x∈(1,+∞)上有两个不同实数解
所以false上x∈(1,+∞)有两个不同实数解
设t=x-1∈(1,+∞),即false.在t∈(1,+∞)上有两有两个不同解
所以false,即false.
22.设函数false,a,b∈R.
(1)若函数false在[0,2]上单调递增,在(2,+∞)单调递减,求实数a的值;
(2)若对任意的实数b∈[0,1]及任意的x∈[-3,3],不等式false恒成立,求实数a的取值范围.
解:(1)false,显然a<0,则false解得false,经检验,符合题意,
∴a的值为false.
不等式false恒成立,即-2≤f(x)≤2,令false,
则false恒成立,则-2≤g(x)≤1恒成立.
则由false解得false
false可化为false恒成立,
先考虑false恒成立,即false,
由false恒成立知,false恒成立,则false,false.
只需证明:false
右边:false
左边:当false时,false,
当false时,false,证毕!
同课章节目录
