京改版七年级数学上册 第三章 简单的几何图形 单元检测试题 (word版 含解析)
文档属性
| 名称 | 京改版七年级数学上册 第三章 简单的几何图形 单元检测试题 (word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 113.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-05 00:00:00 | ||
图片预览


文档简介
第三章
简单的几何图形
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
正方体的顶点数、面数和棱数分别是(
)
A.、、
B.、、
C.、、
D.、、
?
2.
如图所示,从地到达地,最短的路线是(
)
A.
B.
C.
D.
?
3.
按下列长度,、、三点不在一条直线上的是(
)
A.,,
B.,,
C.,,
D.,,
?
4.
下列说法中不正确的是(
)
A.在同一平面内,经过一点能画一条且只能画一条直线与已知直线垂直
B.从直线外一点到这条直线的垂线段叫做点到直线的距离
C.一条直线的垂线可以画无数条
D.连接直线外一点与直线上各点的所有线段中,垂线段最短
?
5.
有下列说法:
①由许多条线段连接而成的图形叫做多边形;
②多边形的边数是不小于的自然数;
③从一个多边形(边数为)的同一个顶点出发,分别连接这个顶点与其余与之不相邻的各顶点,可以把这个多边形分割成个三角形;
④半圆是扇形.
其中正确的结论有(
)
A.个
B.个
C.个
D.个
?
6.
一条直线上依次有,,三点,若,则的长为(?
?
?
?
)
A.
B.
C.
D.或
?
7.
一个正方形切去一个角后,剩余的图形有角(
)
A.个
B.个
C.个
D.个或个或个
?8.
钟表在点分时,它的时针和分针所成的角是(
)
A.
B.
C.
D.
?
9.
下列说法中正确的是(
)
A.一条射线把一个角分成两个角,这条射线是这个角的角平分线
B.点到直线的距离是指从直线外一点到这条直线的垂线的长度
C.若,则点是线段的中点
D.有,,则点在线段上,点在线段外
?
10.
如图,已知,,于点,于点,则下列说法中错误的是(
)
A.
B.
C.、两点间距离就是线段的长度
D.与两平行线间的距离就是线段的长度
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
如图,表示南偏东,表示北偏东,那么=________.
?
12.
如图,直线,被直线所截,如果=,那么的同位角等于________度.
13.
从某一个方向观察一个正六棱柱,可看到如图所示的图形,其中四边形为矩形,、分别是、的中点,若=,=,则这个正六棱柱的侧面积为________.
?
14.
计算:″________.
?
15.
如图,直线、相交于点,平分,则的余角是________,的补角是________,的补角是________.
?
16.
的两边与的两边互相平行,且比的倍少,则的度数为________.
?
17.
半径为的半圆周长是________.
?
18.
将钝角,直角,平角,锐角由小到大依次排列,顺序是________.
?
19.
如图,正方形的边长是,以直线为轴,将正方形旋转一周,所得几何体的左视图的面积是________?(结果保留).
?
20.
墙角处有若干大小相同的小正方体堆成如图所示的立体图形,如果你打算搬走其中部分小正方体(不考虑操作技术的限制),但希望搬完后从正面、从上面、从右面用平行光线照射时,在墙面及地面上的影子不变,那么你最多可以搬走________个小正方体.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
如图,,平分,,求的度数.
?
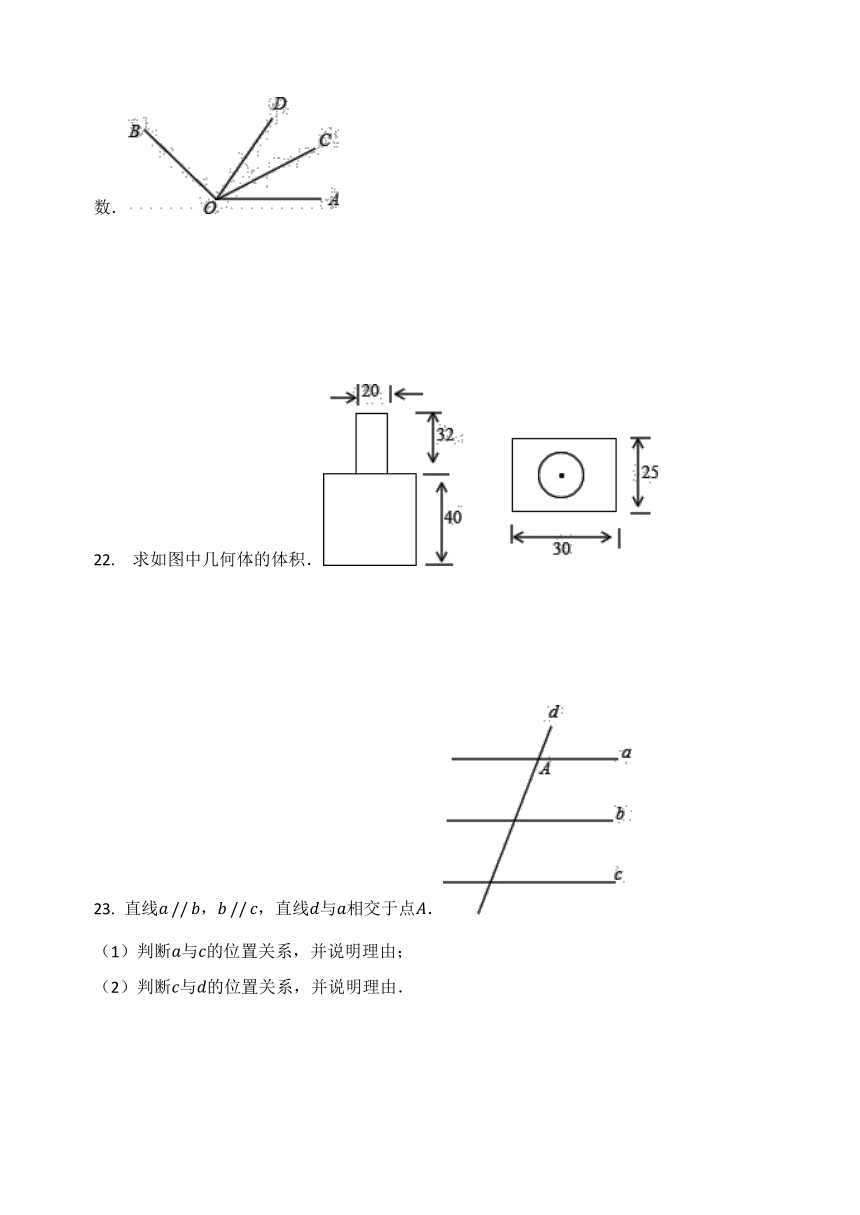
22.
求如图中几何体的体积.
?
23.
直线,,直线与相交于点.
(1)判断与的位置关系,并说明理由;?
(2)判断与的位置关系,并说明理由.
?
24.
(1)补全下面的图形,使之成为长方体的直观图,并标出顶点的字母;
(2)图中与棱平行的棱有________;
(3)图中棱和面的位置关系是________.
?
25.
?
某工程队在修建高速公路时,有时需要将弯曲的道路改直以缩短路程,这样做用到的几何学的原理是________.
如图所示,是的平分线,是的平分线,且,那么直线,的位置关系如何?并说明理由.
?
?
26.
如图,已知,求(请填空)
解:
________
(_____________)
又
?
(_______________)
________
(__________________)
________(________________)
?(_________________)
________
(________________).
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
A
【解答】
解:正方体的顶点数是个,有个面,棱有条.
故选.
2.
【答案】
B
【解答】
解:由题意从地到达地,由图知,
要先到地再到地,是一条直线故已最短.
到有四种选择,根据两点之间线段最短知,路线最短,
因为他们在一条直线上.
故选.
3.
【答案】
C
【解答】
解:、、选项中、、间有等量关系,
选项中、、间没有等量关系.
故选.
4.
【答案】
B
【解答】
、在同一平面内,经过一点能画一条且只能画一条直线与已知直线垂直,正确,不合题意;
、从直线外一点到这条直线的垂线段的长叫做点到直线的距离,故此选项错误,符合题意;
、一条直线的垂线可以画无数条,正确,不合题意;
、连接直线外一点与直线上各点的所有线段中,垂线段最短,正确,不合题意;
5.
【答案】
B
【解答】
解:∵
由许多条线段连接而成的平面图形叫做多边形,
∴
选项①不符合题意;
?
∵
多边形的边数是不小于的自然数,
∴
选项②不符合题意;
?
∵
从一个多边形(边数为)的同一个顶点出发,分别连接这个顶点与其余与之不相邻的各顶点,可以把这个多边形分割成个三角形,
∴
选项③符合题意;
?
∵
半圆是扇形,
∴
选项④符合题意,
∴
正确的结论有个:③、④.
故选:.
6.
【答案】
C
【解答】
解:一条直线上依次有,,三点,,
则,
∴
.
故选.
7.
【答案】
D
【解答】
解:如图所示:
,
故选:.
8.
【答案】
A
【解答】
解;点分时,它的时针和分针所成的角是,
故选:.
9.
【答案】
D
【解答】
解:、从顶点发出,在角内部的一条射线把一个角分成两个相等的角,这条射线叫这个角的平分线.故一条射线把一个角分成两个角,这条射线叫这个角的平分线.错误.
、直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,错误.
、若,则点是线段的中点,当点不在线段上时不成立,错误.
、有,,则点在线段上,点在线段外,正确.
故答案为.
10.
【答案】
D
【解答】
解:、∵
,,
∴
四边形是平行四边形,
∴
,故本选项正确;
、∵
,于点,于点,
∴
四边形是平行四边形,
∴
,故本选项正确;
、∵
是线段,
∴
、两点间距离就是线段的长度,故本选项正确;
、∵
于点,
∴
与两平行线间的距离就是线段的长度,故本选项错误.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
∵
表示南偏东,表示北偏东,
∴
===,
12.
【答案】
【解答】
∵
=,
∴
==,
∴
的同位角为,
13.
【答案】
【解答】
如图,正六边形的边长为、,
垂直平分,
由正六边形的性质可知,=,==,=,
所以,,
正六棱柱的侧面积===.
14.
【答案】
″
【解答】
解:
″″″
″″″″.
故填″
15.
【答案】
,,与
【解答】
解:由图可知的余角是,的补角是,的补角是与.
16.
【答案】
或
【解答】
解:根据题意,得
或
解方程组得或,.
故答案为:或.
17.
【答案】
【解答】
解:半圆周长.
故答案为:.
18.
【答案】
锐角直角钝角平角
【解答】
解:将钝角,直角,平角,锐角由小到大依次排列,顺序是?锐角直角钝角平角,
故答案为:锐角直角钝角平角.
19.
【答案】
【解答】
解:矩形的宽是就是原正方形的边长,矩形的长是原正方形边长的两倍,即,
所得几何体的左视图的面积即矩形的面积,为:.
故答案为:.
20.
【答案】
【解答】
第列最多可以搬走个小正方体;
第列最多可以搬走个小正方体;
第列最多可以搬走个小正方体;
第列最多可以搬走个小正方体;
第列最多可以搬走个小正方体.
=个.
故最多可以搬走个小正方体.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:∵
,
∴
.
∵
平分,
∴
,
∵
,
∴
,解得.
【解答】
解:∵
,
∴
.
∵
平分,
∴
,
∵
,
∴
,解得.
22.
【答案】
解:如图所示:几何体是长方体与圆柱体的组合体,
故其体积为:.
【解答】
解:如图所示:几何体是长方体与圆柱体的组合体,
故其体积为:.
23.
【答案】
解:(1)与的位置关系是平行,
理由是:∵
直线,,
∴
;
(2)与的位置关系是相交,
理由是:∵
,直线与相交于点,
∴
与的位置关系是相交.
【解答】
解:(1)与的位置关系是平行,
理由是:∵
直线,,
∴
;
(2)与的位置关系是相交,
理由是:∵
,直线与相交于点,
∴
与的位置关系是相交.
24.
【答案】
如图即为补全的图形;
、、
平行
【解答】
如图即为补全的图形;
图中与棱平行的棱有、、;
故答案为:、、;
图中棱和面的位置关系是:平行.
故答案为:平行.
25.
【答案】
两点之间,线段最短
直线,的位置关系为:.
理由如下:
∵
是的平分线,是的平分线,
∴
,.
∵
,
∴
,
∴
.
【解答】
解:弯曲的道路改直,使两点处于同一条线段上,两点之间线段最短.
故答案为:两点之间,线段最短.
直线,的位置关系为:.
理由如下:
∵
是的平分线,是的平分线,
∴
,.
∵
,
∴
,
∴
.
26.
【答案】
?
?(两直线平行,同位角相等)
,(等量代换)
,
(内错角相等,两直线平行),?
(两直线平行,同旁内角互补)
,(已知),?
(等式的性质)
【解答】
解:∵
∴
(两直线平行,同位角相等)
又∵
∴
(等量代换)
∴
(内错角相等,两直线平行)
∴
°(两直线平行,同旁内角互补)
∵
°(已知)
∴
°(等式的性质).
故答案为:,两直线平行同位角相等,等量代换,,内错角相等两直线平行,,两直线平行同旁内角互补,已知,°,等式的性质.
简单的几何图形
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
正方体的顶点数、面数和棱数分别是(
)
A.、、
B.、、
C.、、
D.、、
?
2.
如图所示,从地到达地,最短的路线是(
)
A.
B.
C.
D.
?
3.
按下列长度,、、三点不在一条直线上的是(
)
A.,,
B.,,
C.,,
D.,,
?
4.
下列说法中不正确的是(
)
A.在同一平面内,经过一点能画一条且只能画一条直线与已知直线垂直
B.从直线外一点到这条直线的垂线段叫做点到直线的距离
C.一条直线的垂线可以画无数条
D.连接直线外一点与直线上各点的所有线段中,垂线段最短
?
5.
有下列说法:
①由许多条线段连接而成的图形叫做多边形;
②多边形的边数是不小于的自然数;
③从一个多边形(边数为)的同一个顶点出发,分别连接这个顶点与其余与之不相邻的各顶点,可以把这个多边形分割成个三角形;
④半圆是扇形.
其中正确的结论有(
)
A.个
B.个
C.个
D.个
?
6.
一条直线上依次有,,三点,若,则的长为(?
?
?
?
)
A.
B.
C.
D.或
?
7.
一个正方形切去一个角后,剩余的图形有角(
)
A.个
B.个
C.个
D.个或个或个
?8.
钟表在点分时,它的时针和分针所成的角是(
)
A.
B.
C.
D.
?
9.
下列说法中正确的是(
)
A.一条射线把一个角分成两个角,这条射线是这个角的角平分线
B.点到直线的距离是指从直线外一点到这条直线的垂线的长度
C.若,则点是线段的中点
D.有,,则点在线段上,点在线段外
?
10.
如图,已知,,于点,于点,则下列说法中错误的是(
)
A.
B.
C.、两点间距离就是线段的长度
D.与两平行线间的距离就是线段的长度
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
如图,表示南偏东,表示北偏东,那么=________.
?
12.
如图,直线,被直线所截,如果=,那么的同位角等于________度.
13.
从某一个方向观察一个正六棱柱,可看到如图所示的图形,其中四边形为矩形,、分别是、的中点,若=,=,则这个正六棱柱的侧面积为________.
?
14.
计算:″________.
?
15.
如图,直线、相交于点,平分,则的余角是________,的补角是________,的补角是________.
?
16.
的两边与的两边互相平行,且比的倍少,则的度数为________.
?
17.
半径为的半圆周长是________.
?
18.
将钝角,直角,平角,锐角由小到大依次排列,顺序是________.
?
19.
如图,正方形的边长是,以直线为轴,将正方形旋转一周,所得几何体的左视图的面积是________?(结果保留).
?
20.
墙角处有若干大小相同的小正方体堆成如图所示的立体图形,如果你打算搬走其中部分小正方体(不考虑操作技术的限制),但希望搬完后从正面、从上面、从右面用平行光线照射时,在墙面及地面上的影子不变,那么你最多可以搬走________个小正方体.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
如图,,平分,,求的度数.
?
22.
求如图中几何体的体积.
?
23.
直线,,直线与相交于点.
(1)判断与的位置关系,并说明理由;?
(2)判断与的位置关系,并说明理由.
?
24.
(1)补全下面的图形,使之成为长方体的直观图,并标出顶点的字母;
(2)图中与棱平行的棱有________;
(3)图中棱和面的位置关系是________.
?
25.
?
某工程队在修建高速公路时,有时需要将弯曲的道路改直以缩短路程,这样做用到的几何学的原理是________.
如图所示,是的平分线,是的平分线,且,那么直线,的位置关系如何?并说明理由.
?
?
26.
如图,已知,求(请填空)
解:
________
(_____________)
又
?
(_______________)
________
(__________________)
________(________________)
?(_________________)
________
(________________).
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
A
【解答】
解:正方体的顶点数是个,有个面,棱有条.
故选.
2.
【答案】
B
【解答】
解:由题意从地到达地,由图知,
要先到地再到地,是一条直线故已最短.
到有四种选择,根据两点之间线段最短知,路线最短,
因为他们在一条直线上.
故选.
3.
【答案】
C
【解答】
解:、、选项中、、间有等量关系,
选项中、、间没有等量关系.
故选.
4.
【答案】
B
【解答】
、在同一平面内,经过一点能画一条且只能画一条直线与已知直线垂直,正确,不合题意;
、从直线外一点到这条直线的垂线段的长叫做点到直线的距离,故此选项错误,符合题意;
、一条直线的垂线可以画无数条,正确,不合题意;
、连接直线外一点与直线上各点的所有线段中,垂线段最短,正确,不合题意;
5.
【答案】
B
【解答】
解:∵
由许多条线段连接而成的平面图形叫做多边形,
∴
选项①不符合题意;
?
∵
多边形的边数是不小于的自然数,
∴
选项②不符合题意;
?
∵
从一个多边形(边数为)的同一个顶点出发,分别连接这个顶点与其余与之不相邻的各顶点,可以把这个多边形分割成个三角形,
∴
选项③符合题意;
?
∵
半圆是扇形,
∴
选项④符合题意,
∴
正确的结论有个:③、④.
故选:.
6.
【答案】
C
【解答】
解:一条直线上依次有,,三点,,
则,
∴
.
故选.
7.
【答案】
D
【解答】
解:如图所示:
,
故选:.
8.
【答案】
A
【解答】
解;点分时,它的时针和分针所成的角是,
故选:.
9.
【答案】
D
【解答】
解:、从顶点发出,在角内部的一条射线把一个角分成两个相等的角,这条射线叫这个角的平分线.故一条射线把一个角分成两个角,这条射线叫这个角的平分线.错误.
、直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,错误.
、若,则点是线段的中点,当点不在线段上时不成立,错误.
、有,,则点在线段上,点在线段外,正确.
故答案为.
10.
【答案】
D
【解答】
解:、∵
,,
∴
四边形是平行四边形,
∴
,故本选项正确;
、∵
,于点,于点,
∴
四边形是平行四边形,
∴
,故本选项正确;
、∵
是线段,
∴
、两点间距离就是线段的长度,故本选项正确;
、∵
于点,
∴
与两平行线间的距离就是线段的长度,故本选项错误.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
∵
表示南偏东,表示北偏东,
∴
===,
12.
【答案】
【解答】
∵
=,
∴
==,
∴
的同位角为,
13.
【答案】
【解答】
如图,正六边形的边长为、,
垂直平分,
由正六边形的性质可知,=,==,=,
所以,,
正六棱柱的侧面积===.
14.
【答案】
″
【解答】
解:
″″″
″″″″.
故填″
15.
【答案】
,,与
【解答】
解:由图可知的余角是,的补角是,的补角是与.
16.
【答案】
或
【解答】
解:根据题意,得
或
解方程组得或,.
故答案为:或.
17.
【答案】
【解答】
解:半圆周长.
故答案为:.
18.
【答案】
锐角直角钝角平角
【解答】
解:将钝角,直角,平角,锐角由小到大依次排列,顺序是?锐角直角钝角平角,
故答案为:锐角直角钝角平角.
19.
【答案】
【解答】
解:矩形的宽是就是原正方形的边长,矩形的长是原正方形边长的两倍,即,
所得几何体的左视图的面积即矩形的面积,为:.
故答案为:.
20.
【答案】
【解答】
第列最多可以搬走个小正方体;
第列最多可以搬走个小正方体;
第列最多可以搬走个小正方体;
第列最多可以搬走个小正方体;
第列最多可以搬走个小正方体.
=个.
故最多可以搬走个小正方体.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:∵
,
∴
.
∵
平分,
∴
,
∵
,
∴
,解得.
【解答】
解:∵
,
∴
.
∵
平分,
∴
,
∵
,
∴
,解得.
22.
【答案】
解:如图所示:几何体是长方体与圆柱体的组合体,
故其体积为:.
【解答】
解:如图所示:几何体是长方体与圆柱体的组合体,
故其体积为:.
23.
【答案】
解:(1)与的位置关系是平行,
理由是:∵
直线,,
∴
;
(2)与的位置关系是相交,
理由是:∵
,直线与相交于点,
∴
与的位置关系是相交.
【解答】
解:(1)与的位置关系是平行,
理由是:∵
直线,,
∴
;
(2)与的位置关系是相交,
理由是:∵
,直线与相交于点,
∴
与的位置关系是相交.
24.
【答案】
如图即为补全的图形;
、、
平行
【解答】
如图即为补全的图形;
图中与棱平行的棱有、、;
故答案为:、、;
图中棱和面的位置关系是:平行.
故答案为:平行.
25.
【答案】
两点之间,线段最短
直线,的位置关系为:.
理由如下:
∵
是的平分线,是的平分线,
∴
,.
∵
,
∴
,
∴
.
【解答】
解:弯曲的道路改直,使两点处于同一条线段上,两点之间线段最短.
故答案为:两点之间,线段最短.
直线,的位置关系为:.
理由如下:
∵
是的平分线,是的平分线,
∴
,.
∵
,
∴
,
∴
.
26.
【答案】
?
?(两直线平行,同位角相等)
,(等量代换)
,
(内错角相等,两直线平行),?
(两直线平行,同旁内角互补)
,(已知),?
(等式的性质)
【解答】
解:∵
∴
(两直线平行,同位角相等)
又∵
∴
(等量代换)
∴
(内错角相等,两直线平行)
∴
°(两直线平行,同旁内角互补)
∵
°(已知)
∴
°(等式的性质).
故答案为:,两直线平行同位角相等,等量代换,,内错角相等两直线平行,,两直线平行同旁内角互补,已知,°,等式的性质.
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
