2020-2021学年冀教新版九年级下册数学《第32章 投影与视图》单元测试卷 (word版 含解析)
文档属性
| 名称 | 2020-2021学年冀教新版九年级下册数学《第32章 投影与视图》单元测试卷 (word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 185.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-05 00:00:00 | ||
图片预览



文档简介
2020-2021学年冀教新版九年级下册数学《第32章
投影与视图》单元测试卷
一.选择题
1.一个几何体零件如图所示,则从正面看到的图形是( )
A.
B.
C.
D.
2.如图,A,B,C,D是四位同学画出的一个空心圆柱的主视图和俯视图,正确的一组是( )
A.A
B.B
C.C
D.D
3.下列投影现象属于平行投影的是( )
A.手电筒发出的光线所形成的投影
B.太阳光发出的光线所形成的投影
C.路灯发出的光线所形成的投影
D.台灯发出的光线所形成的投影
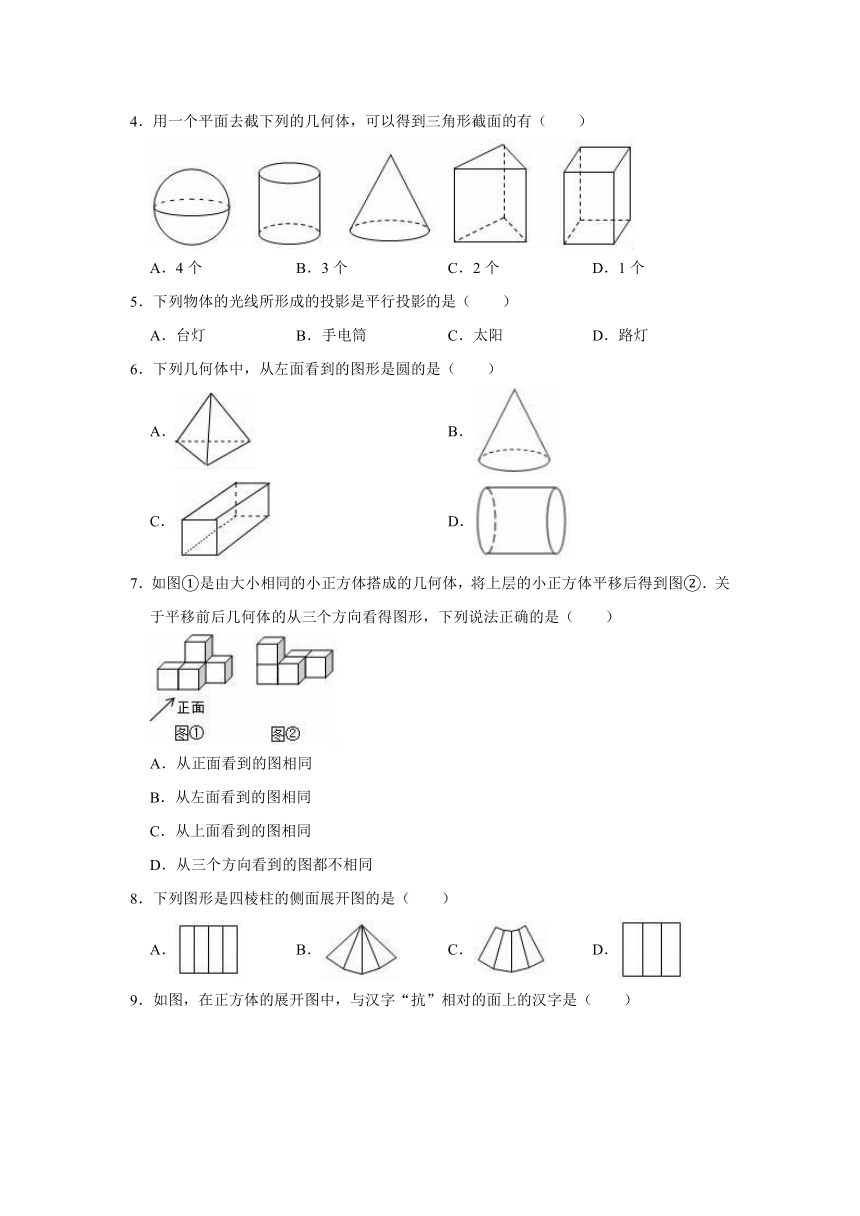
4.用一个平面去截下列的几何体,可以得到三角形截面的有( )
A.4个
B.3个
C.2个
D.1个
5.下列物体的光线所形成的投影是平行投影的是( )
A.台灯
B.手电筒
C.太阳
D.路灯
6.下列几何体中,从左面看到的图形是圆的是( )
A.
B.
C.
D.
7.如图①是由大小相同的小正方体搭成的几何体,将上层的小正方体平移后得到图②.关于平移前后几何体的从三个方向看得图形,下列说法正确的是( )
A.从正面看到的图相同
B.从左面看到的图相同
C.从上面看到的图相同
D.从三个方向看到的图都不相同
8.下列图形是四棱柱的侧面展开图的是( )
A.
B.
C.
D.
9.如图,在正方体的展开图中,与汉字“抗”相对的面上的汉字是( )
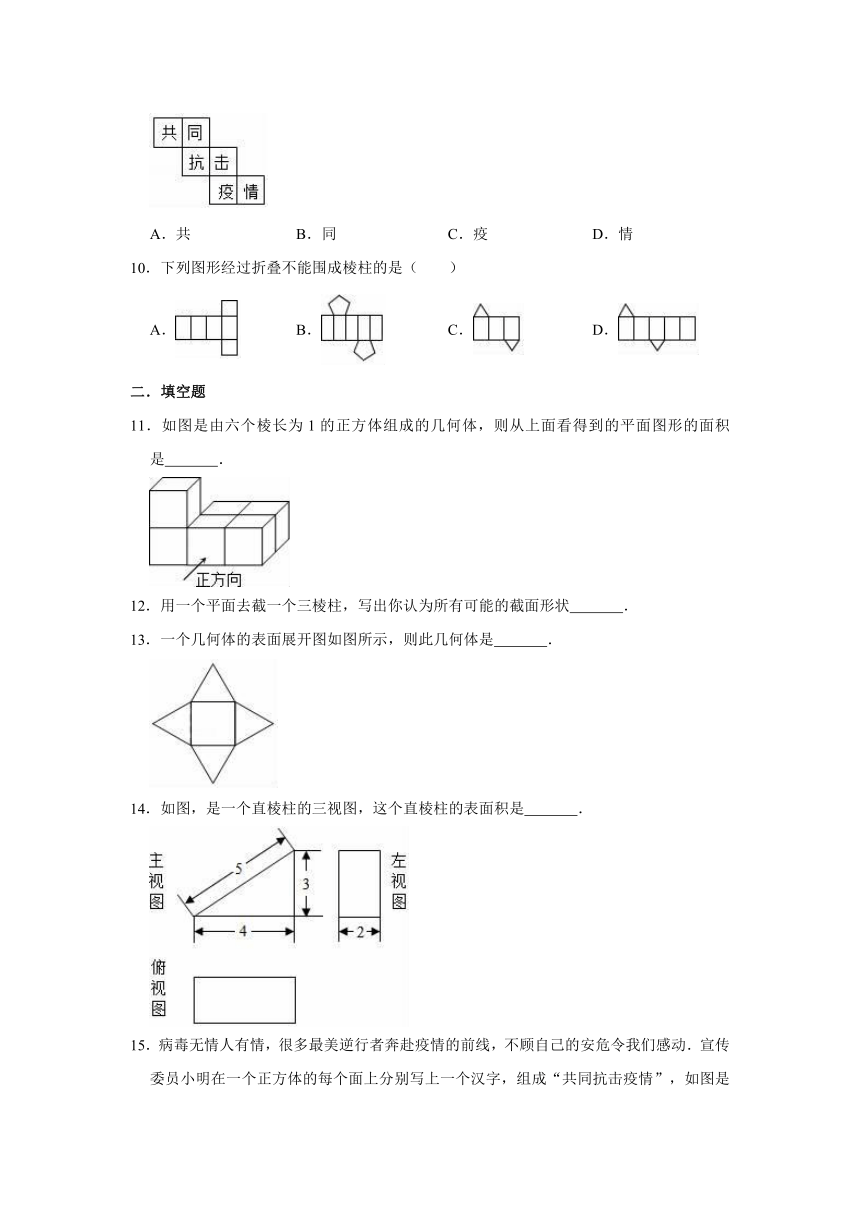
A.共
B.同
C.疫
D.情
10.下列图形经过折叠不能围成棱柱的是( )
A.
B.
C.
D.
二.填空题
11.如图是由六个棱长为1的正方体组成的几何体,则从上面看得到的平面图形的面积是
.
12.用一个平面去截一个三棱柱,写出你认为所有可能的截面形状
.
13.一个几何体的表面展开图如图所示,则此几何体是
.
14.如图,是一个直棱柱的三视图,这个直棱柱的表面积是
.
15.病毒无情人有情,很多最美逆行者奔赴疫情的前线,不顾自己的安危令我们感动.宣传委员小明在一个正方体的每个面上分别写上一个汉字,组成“共同抗击疫情”,如图是该正方体的一种展开图,那么在原正方体中,与汉字“抗”相对的面上的汉字是
.
16.下列图形能围成一个无盖正方体的是
(填序号)
17.图中物体的主视图和俯视图如图所示,请在所给的方格纸中画出该物体的左视图
.
18.如图,物体在灯泡发出的光照射下形成的影子是
投影.(填“平行”或“中心”).
19.如图是由一些相同的小正方体构成的立体图形的三种视图,则构成这个立体图形的小正方体的个数是
个.
20.如图,甲楼AB高18米,乙楼CD坐落在甲楼的正北面,已知当地冬至中午12时,物高与影长的比是1:,已知两楼相距20米,那么甲楼的影子落在乙楼上的高DE=
米.(结果保留根号)
三.解答题
21.填写如图直六棱柱的三个视图的名称.
22.如图,纸板上有5个相连的边是实线的小正方形.
(1)请你再选画1个小正方形使这6个正方形能折叠成一个正方体;(画两种方法)
(2)若正方体相对面上的两个数互为相反数,求x、y的值.
23.在如图的网格中分别画出从正面看,从左面看和从上面看到的形状图.
24.如图所示是长方体的平面展开图,设AB=x,若AD=4x,AN=3x.
(1)求长方形DEFG的周长与长方形ABMN的周长(用字母x进行表示);
(2)若长方形DEFG的周长比长方形ABMN的周长少8,求原长方体的体积.
25.小红想利用阳光下的影长测量学校旗杆AB的高度.如图,他在某一时刻在地面上竖直立一个2米长的标杆CD,测得其影长DE=0.4米.
(1)请在图中画出此时旗杆AB在阳光下的投影BF.
(2)如果BF=1.6,求旗杆AB的高.
26.如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
27.如图,是一个小正方体所搭几何体从上面看得到的平面图形,正方形中的数字表示在该位置小正方体的个数,请你画出它从正面和从左面看得到的平面图形.
参考答案与试题解析
一.选择题
1.解:从正面看,得出是一个较大的矩形,上层的中间是一个小正方形.
故选:A.
2.解:主视图是矩形且中间有两道竖杠,俯视图是两个同心圆,
故选:D.
3.解:手电筒发出的光线所形成的投影、路灯发出的光线所形成的投影和台灯发出的光线所形成的投影都为中心投影;太阳光发出的光线所形成的投影为平行投影.
故选:B.
4.解:用一个平面去截圆锥、三棱柱、四棱柱,可以得到三角形截面,
故选:B.
5.解:太阳光线所形成的投影是平行投影,
故选:C.
6.解:选项A中的几何体的左视图为三角形,因此不符合题意;
选项B中的几何体其左视图为等腰三角形,因此选项B不符合题意;
选项C中的几何体的左视图是长方形,因此选项C不符合题意;
选项D中的几何体,其左视图为圆,因此选项D符合题意,
故选:D.
7.解:图①的三视图为:
图②的三视图为:
故选:C.
8.解:由四棱柱的特点可知:四棱柱的侧面展开图是矩形而且有4条棱.
故选:A.
9.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“共”与“击”是相对面,
“同”与“疫”是相对面,
“抗”与“情”是相对面.
故选:D.
10.解:A可以围成四棱柱,B可以围成五棱柱,C可以围成三棱柱,D选项侧面上多出2个长方形,故不能围成一个三棱柱.
故选:D.
二.填空题
11.解;从上面看第一层是三个小正方形,第二层是中间一个正方形,右边一个小正方形,面积是5,
故答案为:5.
12.解:用一个平面去截一个三棱柱,截面的形状可能为:三角形、四边形、五边形,
故答案为:三角形、四边形、五边形.
13.解:由几何体的表面展开图如可知,该几何体的形状是四棱锥.
故答案为:四棱锥.
14.解:由三视图可得这是一个直三棱柱,它的高为2,
∵32+42=52,
∴这个直三棱柱的底面的直角三角形,
∴这个直三棱柱的表面积为:=36.
故答案为:36.
15.解:根据正方体展开图的特征,“相间、Z端是对面”可得,
“抗”的对面是“情”,
故答案为:情.
16.解:由四棱柱四个侧面和底面的特征可知,①②④⑤可以拼成无盖的正方体,而③⑥拼成的是有两面重合,
故一个无盖的正方体盒子的平面展开图可以是下列图形中的是①②④⑤.
故答案为:①②④⑤.
17.解:.
18.解:由于光源是由一点发出的,因此是中心投影,
故答案为:中心.
19.解:由俯视图易得最底层有6个正方体,第二层有2个正方体,则构成这个立体图形的小正方体的个数是6+2=8个.
故答案为:8.
20.解:设冬天太阳最低时,甲楼最高处A点的影子落在乙楼的E处,那么图中ED的长度就是甲楼的影子在乙楼上的高度,
设FE⊥AB于点F,那么在△AEF中,∠AFE=90°,EF=20米.
∵物高与影长的比是1:,
∴=,
则AF=EF=10,
故DE=FB=18﹣10.
故答案为(18﹣10)
三.解答题
21.解:如图所示:
22.解:(1)任选两种方法:
(2)根据题意,得3x+1+x+3=0,
解得x=﹣1,
x+y=0
解得y=1.
23.解:如图所示:
24.解:(1)∵AB=x,若AD=4x,AN=3x,
∴长方形DEFG的周长为2(x+2x)=6x,
长方形ABMN的周长为2(x+3x)=8x;
(2)依题意得8x﹣6x=8,
解得:x=4,
原长方体的容积为x?2x?3x=6x3,
将x=4代入,可得体积6x3=384.
故原长方体的体积是384.
25.解:(1)连结CE,过A点作AF∥CE交BD于F,则BF为所求,如图;
(2)∵AF∥CE,
∴∠AFB=∠CED,
而∠ABF=∠CDE=90°,
∴△ABF∽△CDE,
∴=,即=,
∴AB=8(m).
答:旗杆AB的高为8m.
26.(1)解:如图,点O为灯泡所在的位置,
线段FH为小亮在灯光下形成的影子.
(2)解:由已知可得,=,
∴=,
∴OD=4.
∴灯泡的高为4m.
27.解:
投影与视图》单元测试卷
一.选择题
1.一个几何体零件如图所示,则从正面看到的图形是( )
A.
B.
C.
D.
2.如图,A,B,C,D是四位同学画出的一个空心圆柱的主视图和俯视图,正确的一组是( )
A.A
B.B
C.C
D.D
3.下列投影现象属于平行投影的是( )
A.手电筒发出的光线所形成的投影
B.太阳光发出的光线所形成的投影
C.路灯发出的光线所形成的投影
D.台灯发出的光线所形成的投影
4.用一个平面去截下列的几何体,可以得到三角形截面的有( )
A.4个
B.3个
C.2个
D.1个
5.下列物体的光线所形成的投影是平行投影的是( )
A.台灯
B.手电筒
C.太阳
D.路灯
6.下列几何体中,从左面看到的图形是圆的是( )
A.
B.
C.
D.
7.如图①是由大小相同的小正方体搭成的几何体,将上层的小正方体平移后得到图②.关于平移前后几何体的从三个方向看得图形,下列说法正确的是( )
A.从正面看到的图相同
B.从左面看到的图相同
C.从上面看到的图相同
D.从三个方向看到的图都不相同
8.下列图形是四棱柱的侧面展开图的是( )
A.
B.
C.
D.
9.如图,在正方体的展开图中,与汉字“抗”相对的面上的汉字是( )
A.共
B.同
C.疫
D.情
10.下列图形经过折叠不能围成棱柱的是( )
A.
B.
C.
D.
二.填空题
11.如图是由六个棱长为1的正方体组成的几何体,则从上面看得到的平面图形的面积是
.
12.用一个平面去截一个三棱柱,写出你认为所有可能的截面形状
.
13.一个几何体的表面展开图如图所示,则此几何体是
.
14.如图,是一个直棱柱的三视图,这个直棱柱的表面积是
.
15.病毒无情人有情,很多最美逆行者奔赴疫情的前线,不顾自己的安危令我们感动.宣传委员小明在一个正方体的每个面上分别写上一个汉字,组成“共同抗击疫情”,如图是该正方体的一种展开图,那么在原正方体中,与汉字“抗”相对的面上的汉字是
.
16.下列图形能围成一个无盖正方体的是
(填序号)
17.图中物体的主视图和俯视图如图所示,请在所给的方格纸中画出该物体的左视图
.
18.如图,物体在灯泡发出的光照射下形成的影子是
投影.(填“平行”或“中心”).
19.如图是由一些相同的小正方体构成的立体图形的三种视图,则构成这个立体图形的小正方体的个数是
个.
20.如图,甲楼AB高18米,乙楼CD坐落在甲楼的正北面,已知当地冬至中午12时,物高与影长的比是1:,已知两楼相距20米,那么甲楼的影子落在乙楼上的高DE=
米.(结果保留根号)
三.解答题
21.填写如图直六棱柱的三个视图的名称.
22.如图,纸板上有5个相连的边是实线的小正方形.
(1)请你再选画1个小正方形使这6个正方形能折叠成一个正方体;(画两种方法)
(2)若正方体相对面上的两个数互为相反数,求x、y的值.
23.在如图的网格中分别画出从正面看,从左面看和从上面看到的形状图.
24.如图所示是长方体的平面展开图,设AB=x,若AD=4x,AN=3x.
(1)求长方形DEFG的周长与长方形ABMN的周长(用字母x进行表示);
(2)若长方形DEFG的周长比长方形ABMN的周长少8,求原长方体的体积.
25.小红想利用阳光下的影长测量学校旗杆AB的高度.如图,他在某一时刻在地面上竖直立一个2米长的标杆CD,测得其影长DE=0.4米.
(1)请在图中画出此时旗杆AB在阳光下的投影BF.
(2)如果BF=1.6,求旗杆AB的高.
26.如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
27.如图,是一个小正方体所搭几何体从上面看得到的平面图形,正方形中的数字表示在该位置小正方体的个数,请你画出它从正面和从左面看得到的平面图形.
参考答案与试题解析
一.选择题
1.解:从正面看,得出是一个较大的矩形,上层的中间是一个小正方形.
故选:A.
2.解:主视图是矩形且中间有两道竖杠,俯视图是两个同心圆,
故选:D.
3.解:手电筒发出的光线所形成的投影、路灯发出的光线所形成的投影和台灯发出的光线所形成的投影都为中心投影;太阳光发出的光线所形成的投影为平行投影.
故选:B.
4.解:用一个平面去截圆锥、三棱柱、四棱柱,可以得到三角形截面,
故选:B.
5.解:太阳光线所形成的投影是平行投影,
故选:C.
6.解:选项A中的几何体的左视图为三角形,因此不符合题意;
选项B中的几何体其左视图为等腰三角形,因此选项B不符合题意;
选项C中的几何体的左视图是长方形,因此选项C不符合题意;
选项D中的几何体,其左视图为圆,因此选项D符合题意,
故选:D.
7.解:图①的三视图为:
图②的三视图为:
故选:C.
8.解:由四棱柱的特点可知:四棱柱的侧面展开图是矩形而且有4条棱.
故选:A.
9.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“共”与“击”是相对面,
“同”与“疫”是相对面,
“抗”与“情”是相对面.
故选:D.
10.解:A可以围成四棱柱,B可以围成五棱柱,C可以围成三棱柱,D选项侧面上多出2个长方形,故不能围成一个三棱柱.
故选:D.
二.填空题
11.解;从上面看第一层是三个小正方形,第二层是中间一个正方形,右边一个小正方形,面积是5,
故答案为:5.
12.解:用一个平面去截一个三棱柱,截面的形状可能为:三角形、四边形、五边形,
故答案为:三角形、四边形、五边形.
13.解:由几何体的表面展开图如可知,该几何体的形状是四棱锥.
故答案为:四棱锥.
14.解:由三视图可得这是一个直三棱柱,它的高为2,
∵32+42=52,
∴这个直三棱柱的底面的直角三角形,
∴这个直三棱柱的表面积为:=36.
故答案为:36.
15.解:根据正方体展开图的特征,“相间、Z端是对面”可得,
“抗”的对面是“情”,
故答案为:情.
16.解:由四棱柱四个侧面和底面的特征可知,①②④⑤可以拼成无盖的正方体,而③⑥拼成的是有两面重合,
故一个无盖的正方体盒子的平面展开图可以是下列图形中的是①②④⑤.
故答案为:①②④⑤.
17.解:.
18.解:由于光源是由一点发出的,因此是中心投影,
故答案为:中心.
19.解:由俯视图易得最底层有6个正方体,第二层有2个正方体,则构成这个立体图形的小正方体的个数是6+2=8个.
故答案为:8.
20.解:设冬天太阳最低时,甲楼最高处A点的影子落在乙楼的E处,那么图中ED的长度就是甲楼的影子在乙楼上的高度,
设FE⊥AB于点F,那么在△AEF中,∠AFE=90°,EF=20米.
∵物高与影长的比是1:,
∴=,
则AF=EF=10,
故DE=FB=18﹣10.
故答案为(18﹣10)
三.解答题
21.解:如图所示:
22.解:(1)任选两种方法:
(2)根据题意,得3x+1+x+3=0,
解得x=﹣1,
x+y=0
解得y=1.
23.解:如图所示:
24.解:(1)∵AB=x,若AD=4x,AN=3x,
∴长方形DEFG的周长为2(x+2x)=6x,
长方形ABMN的周长为2(x+3x)=8x;
(2)依题意得8x﹣6x=8,
解得:x=4,
原长方体的容积为x?2x?3x=6x3,
将x=4代入,可得体积6x3=384.
故原长方体的体积是384.
25.解:(1)连结CE,过A点作AF∥CE交BD于F,则BF为所求,如图;
(2)∵AF∥CE,
∴∠AFB=∠CED,
而∠ABF=∠CDE=90°,
∴△ABF∽△CDE,
∴=,即=,
∴AB=8(m).
答:旗杆AB的高为8m.
26.(1)解:如图,点O为灯泡所在的位置,
线段FH为小亮在灯光下形成的影子.
(2)解:由已知可得,=,
∴=,
∴OD=4.
∴灯泡的高为4m.
27.解:
