人教版九年级数学上册24.1.2垂直于弦的直径 课件(18张ppt)
文档属性
| 名称 | 人教版九年级数学上册24.1.2垂直于弦的直径 课件(18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
人教版九年级上册
24.1.2垂直于弦的直径
.
观图形之美
赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦长)是37.4m,拱高(弧的中点到弦的距离)为7.2m,
你能求出赵州桥主桥拱的半径吗?
观图形之美
把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?你能证明你的结论吗?
可以发现:圆是轴对称图形,任何一条直径所在直线都是它的对称轴.
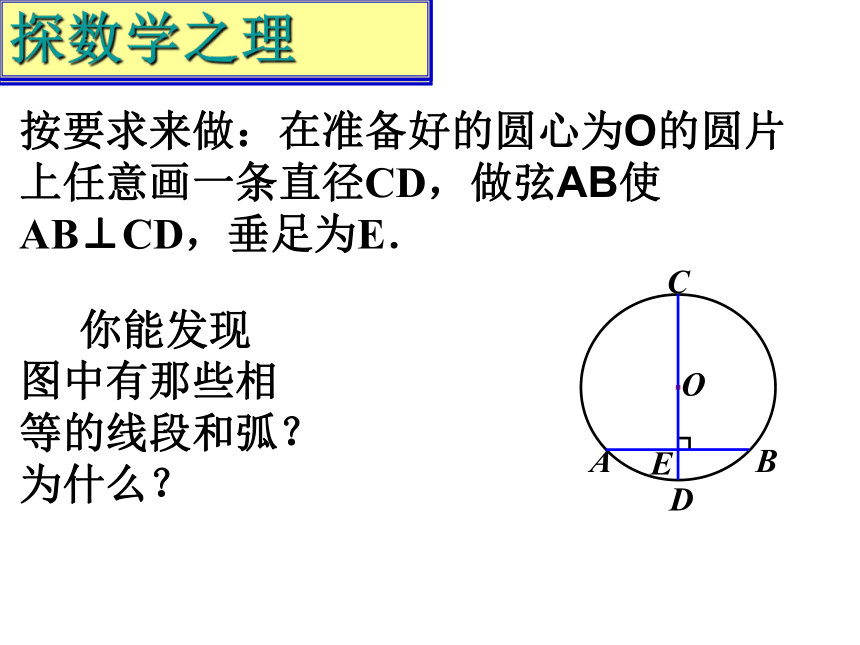
按要求来做:在准备好的圆心为O的圆片上任意画一条直径CD,做弦AB使AB⊥CD,垂足为E.
你能发现图中有那些相等的线段和弧?为什么?
☆个体预习生成
探数学之理
·
O
A
B
C
D
E
垂径定理
·
O
A
B
C
D
E
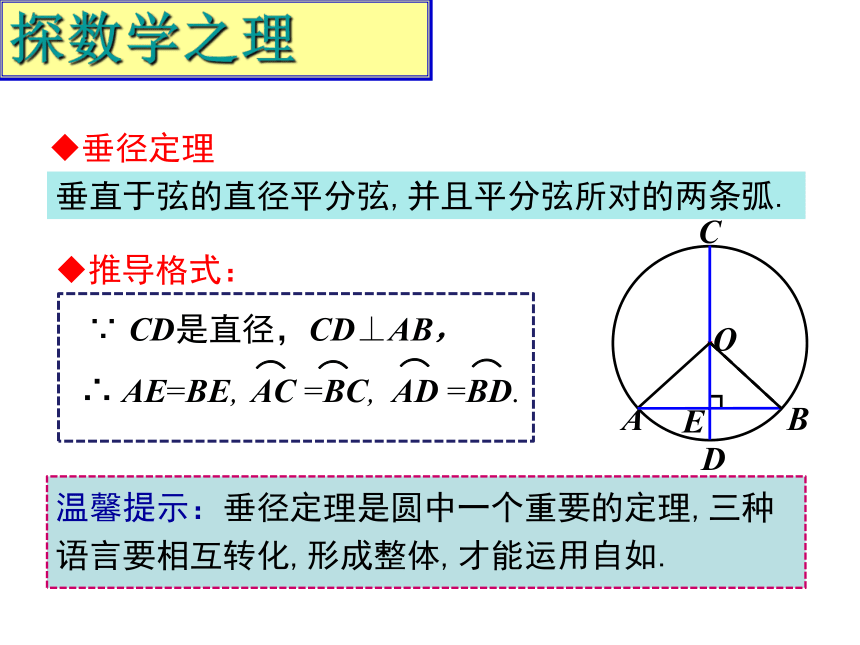
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
∵
CD是直径,CD⊥AB,
∴
AE=BE,
⌒
⌒
AC
=BC,
⌒
⌒
AD
=BD.
推导格式:
温馨提示:垂径定理是圆中一个重要的定理,三种语言要相互转化,形成整体,才能运用自如.
探数学之理
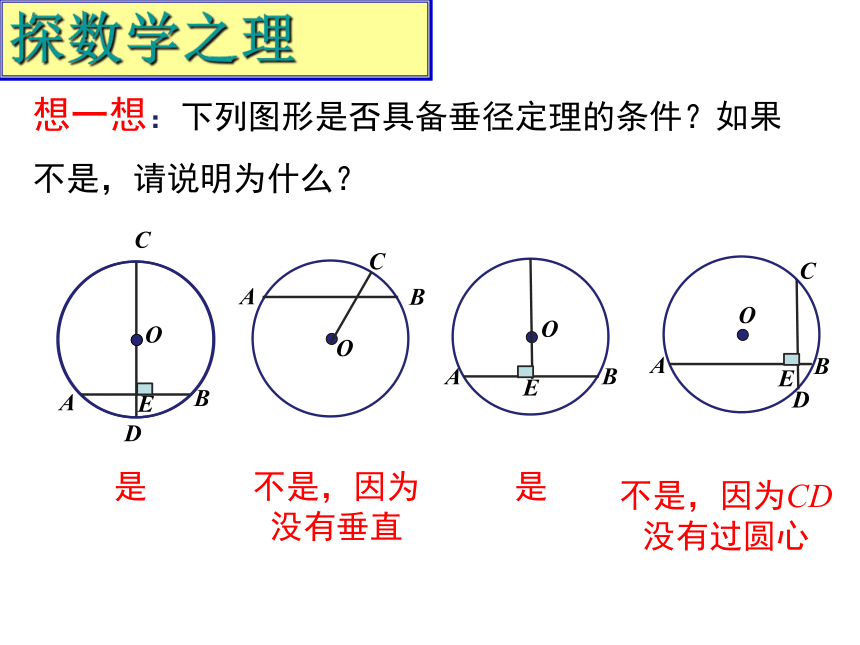
想一想:下列图形是否具备垂径定理的条件?如果不是,请说明为什么?
是
不是,因为没有垂直
是
不是,因为CD没有过圆心
A
B
O
C
D
E
O
A
B
C
A
B
O
E
A
B
D
C
O
E
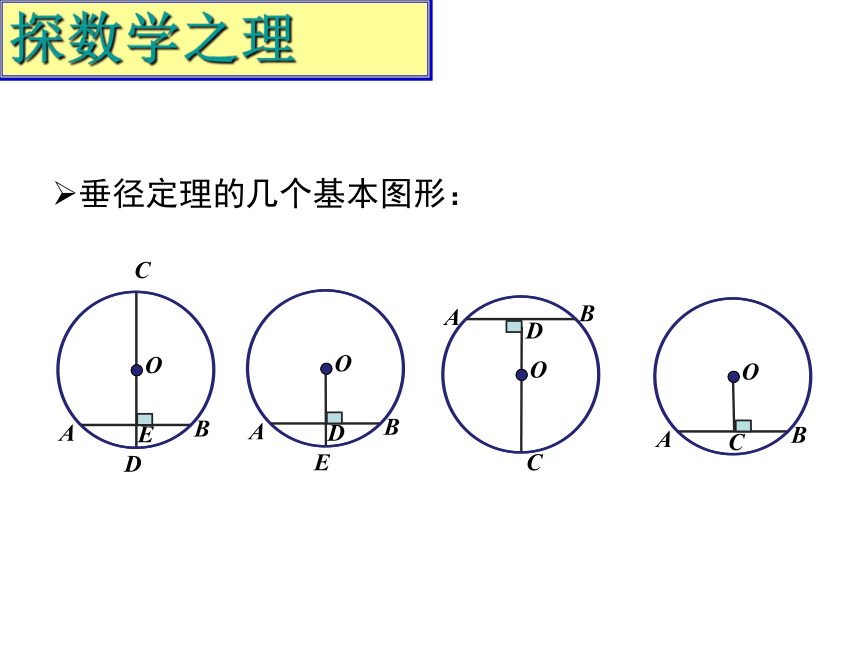
探数学之理
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
D
C
A
B
O
C
探数学之理
如果把垂径定理(垂直于弦的直径平分弦,并且平分弦所对的两条弧)结论与题设交换一条或两条,命题是真命题吗?
①过圆心
;②垂直于弦;
③平分弦;
④平分弦所对的优弧
;
⑤平分弦所对的劣弧.
上述五个条件中的任何两个条件都可以推出其他三个结论吗?
思考探索
集众人之慧
D
O
A
B
E
C
举例证明其中一种组合方法
已知:
求证:
①
CD是直径
②
CD⊥AB,垂足为E
③
AE=BE
④
AC=BC
⑤
AD=BD
⌒
⌒
⌒
⌒
证明猜想
集众人之慧
平分弦
的直径垂直于弦,并且平分弦所对的弧.
垂径定理的推论
集众人之慧
(不是直径)
·
O
A
B
C
D
特别说明:
圆的两条直径是互相平分的.
例1.如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径.
.
A
E
B
O
展数学之翼
注意:求圆的半径通常要构造直角三角形,常用的辅助线有两条(1)过圆心作弦的垂线,(2)连接圆心和弦的端点得半径.
变式1:如图在
⊙O中,弦AB的长为
8
cm,
⊙O的半径为
5
cm,求圆心O到弦AB的距离.
变式2:如图在
⊙O中,
⊙O的半径为10cm,圆心O到AB的距离是6cm,求弦AB的长.
·
O
A
B
展数学之翼
例2
.赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦长)是37.4m,拱高(弧的中点到弦的距离)为7.2m,
你能求出赵州桥主桥拱的半径吗?
展数学之翼
解:如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC垂足为D,与弧AB交于点C,则D是AB的中点,C是弧AB的中点,CD就是拱高.
∴
AB=37m,CD=7.23m.
解得R≈27.3(m).
即主桥拱半径约为27.3m.
=18.52+(R-7.23)2
∴
AD=
AB=18.5m,
OD=OC-CD=R-7.23.
说出你这节课的收获和体验,让大家与你一起分享!!!
享智慧之果
垂径定理
内容
推论
辅助线
一条直线满足:①过圆心;②垂直于弦;
③平分弦(不是直径);
④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论(“知二推三”)
垂直于弦的直径平分弦,
并且平分弦所对的两条弧
两条辅助线:
连半径,作垂直
构造Rt△利用勾股定理计算或建立方程.
基本图形及变式图形
享智慧之果
作业:
1.P88习题24.1
第8题、第10题;
2.智慧学习P83
.
人教版九年级上册
24.1.2垂直于弦的直径
.
观图形之美
赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦长)是37.4m,拱高(弧的中点到弦的距离)为7.2m,
你能求出赵州桥主桥拱的半径吗?
观图形之美
把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?你能证明你的结论吗?
可以发现:圆是轴对称图形,任何一条直径所在直线都是它的对称轴.
按要求来做:在准备好的圆心为O的圆片上任意画一条直径CD,做弦AB使AB⊥CD,垂足为E.
你能发现图中有那些相等的线段和弧?为什么?
☆个体预习生成
探数学之理
·
O
A
B
C
D
E
垂径定理
·
O
A
B
C
D
E
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
∵
CD是直径,CD⊥AB,
∴
AE=BE,
⌒
⌒
AC
=BC,
⌒
⌒
AD
=BD.
推导格式:
温馨提示:垂径定理是圆中一个重要的定理,三种语言要相互转化,形成整体,才能运用自如.
探数学之理
想一想:下列图形是否具备垂径定理的条件?如果不是,请说明为什么?
是
不是,因为没有垂直
是
不是,因为CD没有过圆心
A
B
O
C
D
E
O
A
B
C
A
B
O
E
A
B
D
C
O
E
探数学之理
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
D
C
A
B
O
C
探数学之理
如果把垂径定理(垂直于弦的直径平分弦,并且平分弦所对的两条弧)结论与题设交换一条或两条,命题是真命题吗?
①过圆心
;②垂直于弦;
③平分弦;
④平分弦所对的优弧
;
⑤平分弦所对的劣弧.
上述五个条件中的任何两个条件都可以推出其他三个结论吗?
思考探索
集众人之慧
D
O
A
B
E
C
举例证明其中一种组合方法
已知:
求证:
①
CD是直径
②
CD⊥AB,垂足为E
③
AE=BE
④
AC=BC
⑤
AD=BD
⌒
⌒
⌒
⌒
证明猜想
集众人之慧
平分弦
的直径垂直于弦,并且平分弦所对的弧.
垂径定理的推论
集众人之慧
(不是直径)
·
O
A
B
C
D
特别说明:
圆的两条直径是互相平分的.
例1.如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径.
.
A
E
B
O
展数学之翼
注意:求圆的半径通常要构造直角三角形,常用的辅助线有两条(1)过圆心作弦的垂线,(2)连接圆心和弦的端点得半径.
变式1:如图在
⊙O中,弦AB的长为
8
cm,
⊙O的半径为
5
cm,求圆心O到弦AB的距离.
变式2:如图在
⊙O中,
⊙O的半径为10cm,圆心O到AB的距离是6cm,求弦AB的长.
·
O
A
B
展数学之翼
例2
.赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦长)是37.4m,拱高(弧的中点到弦的距离)为7.2m,
你能求出赵州桥主桥拱的半径吗?
展数学之翼
解:如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC垂足为D,与弧AB交于点C,则D是AB的中点,C是弧AB的中点,CD就是拱高.
∴
AB=37m,CD=7.23m.
解得R≈27.3(m).
即主桥拱半径约为27.3m.
=18.52+(R-7.23)2
∴
AD=
AB=18.5m,
OD=OC-CD=R-7.23.
说出你这节课的收获和体验,让大家与你一起分享!!!
享智慧之果
垂径定理
内容
推论
辅助线
一条直线满足:①过圆心;②垂直于弦;
③平分弦(不是直径);
④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论(“知二推三”)
垂直于弦的直径平分弦,
并且平分弦所对的两条弧
两条辅助线:
连半径,作垂直
构造Rt△利用勾股定理计算或建立方程.
基本图形及变式图形
享智慧之果
作业:
1.P88习题24.1
第8题、第10题;
2.智慧学习P83
.
同课章节目录
