五年级上册数学课件-6.4组合图形的面积 16页PPT 人教版
文档属性
| 名称 | 五年级上册数学课件-6.4组合图形的面积 16页PPT 人教版 |  | |
| 格式 | pptx | ||
| 文件大小 | 944.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 17:17:30 | ||
图片预览




文档简介
课件简介
本课件紧扣课本内容,祥细演示了计算组合图形的两种常用思路:把原图形拆分成若干规则图形和把空缺部分补全成规则图形。让学生一目了然,易于理解和记忆。
演示时本张可删除
组 合 图 形 的 面 积
实际生活中经常用到组合图形,例如:
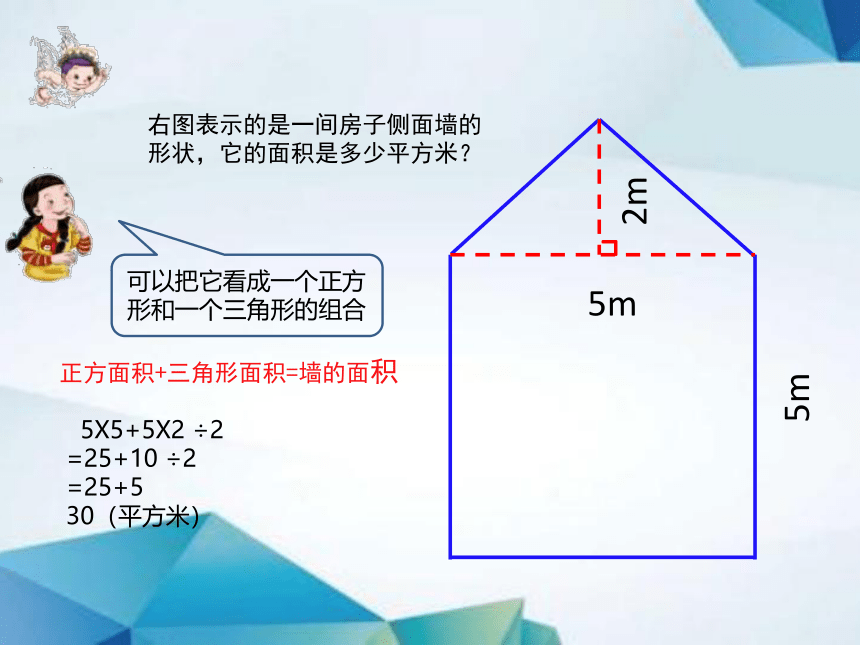
5m
5m
右图表示的是一间房子侧面墙的形状,它的面积是多少平方米?
2m
可以把它看成一个正方形和一个三角形的组合
正方面积+三角形面积=墙的面积
5X5+5X2 ÷2
=25+10 ÷2
=25+5
30(平方米)
5m
5m
你还有其它办法吗?
2m
也可以把它分成两个完全一样的梯形
梯形的下底:5+2=7(米)
梯形的高:5 ÷ 2=2.5(米)
一个梯形的面积:
(5+7)X2.5 ÷2
=12 X2 ÷2
=30 ÷2
=15(平方米)
墙的面积:15X2=30(平方米)
答:墙的面积是30平方米。
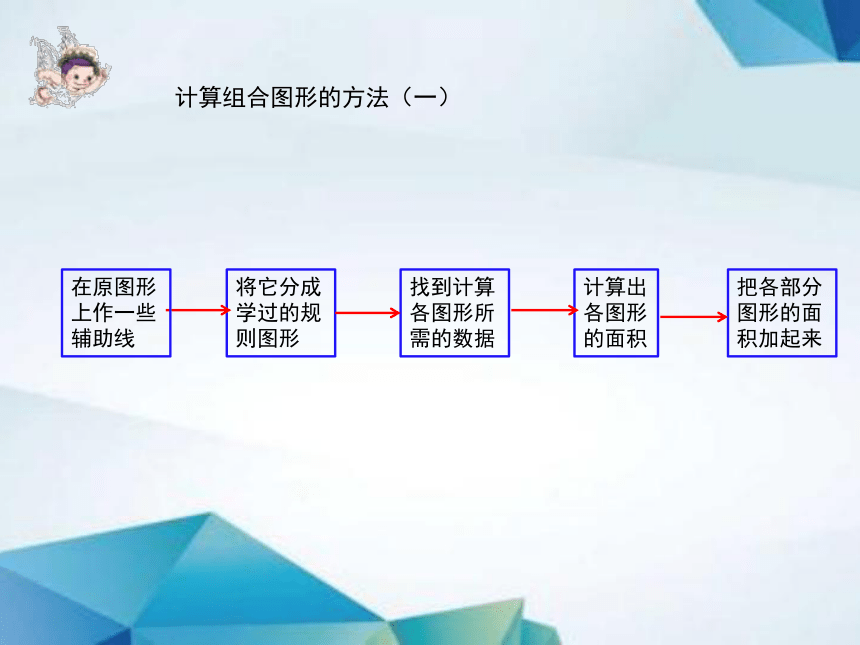
将它分成学过的规则图形
找到计算各图形所需的数据
计算出各图形的面积
把各部分图形的面积加起来
在原图形上作一些辅助线
计算组合图形的方法(一)
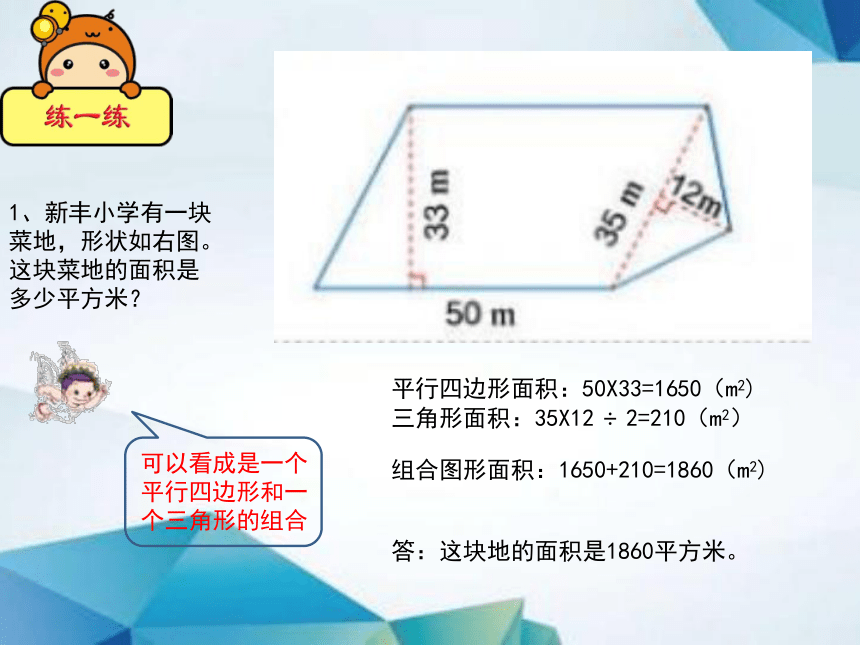
1、新丰小学有一块菜地,形状如右图。这块菜地的面积是多少平方米?
可以看成是一个平行四边形和一个三角形的组合
平行四边形面积:50X33=1650(m2)
三角形面积:35X12 ÷ 2=210(m2)
组合图形面积:1650+210=1860(m2)
答:这块地的面积是1860平方米。
2、一面中国少年先锋队中队旗的面积是多少?
可以看成在一个长方形中剪去一个三角形
队旗面积=长方形面积-三角形面积
长方形面积:80X(30+30)=4800(cm2)
三角形面积:(30+30)X20 ÷ 2
=60X20 ÷ 2
=1200 ÷ 2
=600(cm2)
答:队旗的面积是600平方厘米。
将它补全成学过的规则图形
找到计算各图形所需的数据
计算补全和空缺图形的面积
补全图形面积减去空缺面积
在原图形上作一些辅助线
计算组合图形的方法(二)
有一片不规则的树叶,你能知道它的面积吗?
图中每个小方格的面积是1,请你估计这片叶子的面积。
方格纸上满格的有18格,不满格的也有18格。
如果把不满一格的按半格计算,这片叶子的面积大约是27平方厘米。
我是将叶子的形状近似转化成平行四边形……
S=ah
=5X6
=30 (cm2)
有一块地近似平行四边形,底是43m,高是20.1m。这块地的面积约是多少平方米?(得数保留整数)
S=ah
=43X20.1
≈ 864(平方米)
答:这块地的面积约是864平方米。
图中每个小方格的面积是1(cm2),计算阴影部分的面积。
解法一:如左图作一条辅助线(红色),将原图分成一个梯形和一个三角形。
梯形:上底4cm,下底5cm,高2cm;
三角形:底5cm,高6cm。
原图形面积:(4+5)X2 ÷ 2+5X6 ÷ 2
=9X2÷ 2+30÷ 2
=18÷ 2+15
=9+15
=24(cm2)
图中每个小方格的面积是1(cm2),计算阴影部分的面积。
解法二:如左图作一条辅助线(红色),将原图分成一个梯形和一个三角形。
梯形:上底5cm,下底2cm,高4cm;
三角形:底5cm,高4cm。
原图形面积:(5+2)X4 ÷ 2+5X4 ÷ 2
=7X4÷ 2+20÷ 2
=28÷ 2+10
=14+10
=24(cm2)
观察图中不规则的地方有什么特点。
通过割补后变成了一个长方形
S=ab
=8X4
=32(cm2)
本课件紧扣课本内容,祥细演示了计算组合图形的两种常用思路:把原图形拆分成若干规则图形和把空缺部分补全成规则图形。让学生一目了然,易于理解和记忆。
演示时本张可删除
组 合 图 形 的 面 积
实际生活中经常用到组合图形,例如:
5m
5m
右图表示的是一间房子侧面墙的形状,它的面积是多少平方米?
2m
可以把它看成一个正方形和一个三角形的组合
正方面积+三角形面积=墙的面积
5X5+5X2 ÷2
=25+10 ÷2
=25+5
30(平方米)
5m
5m
你还有其它办法吗?
2m
也可以把它分成两个完全一样的梯形
梯形的下底:5+2=7(米)
梯形的高:5 ÷ 2=2.5(米)
一个梯形的面积:
(5+7)X2.5 ÷2
=12 X2 ÷2
=30 ÷2
=15(平方米)
墙的面积:15X2=30(平方米)
答:墙的面积是30平方米。
将它分成学过的规则图形
找到计算各图形所需的数据
计算出各图形的面积
把各部分图形的面积加起来
在原图形上作一些辅助线
计算组合图形的方法(一)
1、新丰小学有一块菜地,形状如右图。这块菜地的面积是多少平方米?
可以看成是一个平行四边形和一个三角形的组合
平行四边形面积:50X33=1650(m2)
三角形面积:35X12 ÷ 2=210(m2)
组合图形面积:1650+210=1860(m2)
答:这块地的面积是1860平方米。
2、一面中国少年先锋队中队旗的面积是多少?
可以看成在一个长方形中剪去一个三角形
队旗面积=长方形面积-三角形面积
长方形面积:80X(30+30)=4800(cm2)
三角形面积:(30+30)X20 ÷ 2
=60X20 ÷ 2
=1200 ÷ 2
=600(cm2)
答:队旗的面积是600平方厘米。
将它补全成学过的规则图形
找到计算各图形所需的数据
计算补全和空缺图形的面积
补全图形面积减去空缺面积
在原图形上作一些辅助线
计算组合图形的方法(二)
有一片不规则的树叶,你能知道它的面积吗?
图中每个小方格的面积是1,请你估计这片叶子的面积。
方格纸上满格的有18格,不满格的也有18格。
如果把不满一格的按半格计算,这片叶子的面积大约是27平方厘米。
我是将叶子的形状近似转化成平行四边形……
S=ah
=5X6
=30 (cm2)
有一块地近似平行四边形,底是43m,高是20.1m。这块地的面积约是多少平方米?(得数保留整数)
S=ah
=43X20.1
≈ 864(平方米)
答:这块地的面积约是864平方米。
图中每个小方格的面积是1(cm2),计算阴影部分的面积。
解法一:如左图作一条辅助线(红色),将原图分成一个梯形和一个三角形。
梯形:上底4cm,下底5cm,高2cm;
三角形:底5cm,高6cm。
原图形面积:(4+5)X2 ÷ 2+5X6 ÷ 2
=9X2÷ 2+30÷ 2
=18÷ 2+15
=9+15
=24(cm2)
图中每个小方格的面积是1(cm2),计算阴影部分的面积。
解法二:如左图作一条辅助线(红色),将原图分成一个梯形和一个三角形。
梯形:上底5cm,下底2cm,高4cm;
三角形:底5cm,高4cm。
原图形面积:(5+2)X4 ÷ 2+5X4 ÷ 2
=7X4÷ 2+20÷ 2
=28÷ 2+10
=14+10
=24(cm2)
观察图中不规则的地方有什么特点。
通过割补后变成了一个长方形
S=ab
=8X4
=32(cm2)
