初中数学人教版九年级上册24.4 弧长及扇形的面积练习题(Word版 含解析)
文档属性
| 名称 | 初中数学人教版九年级上册24.4 弧长及扇形的面积练习题(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 190.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 12:17:22 | ||
图片预览


文档简介
初中数学人教版九年级上册第二十四章弧长和扇形的面积练习题
一、选择题
若圆锥的底面半径为3,母线长为5,则它的侧面展开图的圆心角等于
A.
B.
C.
D.
有一条弧的长为,半径为2cm,则这条弧所对的圆心角的度数是
A.
B.
C.
D.
已知扇形的圆心角为,半径长为3,则该扇形的面积为
A.
B.
C.
D.
用一个半径为30,圆心角为的扇形围成一个圆锥,则这个圆锥的底面半径是
A.
10
B.
20
C.
D.
钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是.
A.
B.
C.
D.
已知扇形的半径为3,弧长为,则此扇形的圆心角的度数为
A.
B.
C.
D.
如图,在中,,,,则阴影部分的面积是???
A.
B.
C.
D.
圆柱形水桶的底面周长为,高为,它的侧面积是
A.
B.
C.
D.
如图,AB是的直径,CD是弦,,,则阴影部分的面积是
A.
B.
C.
D.
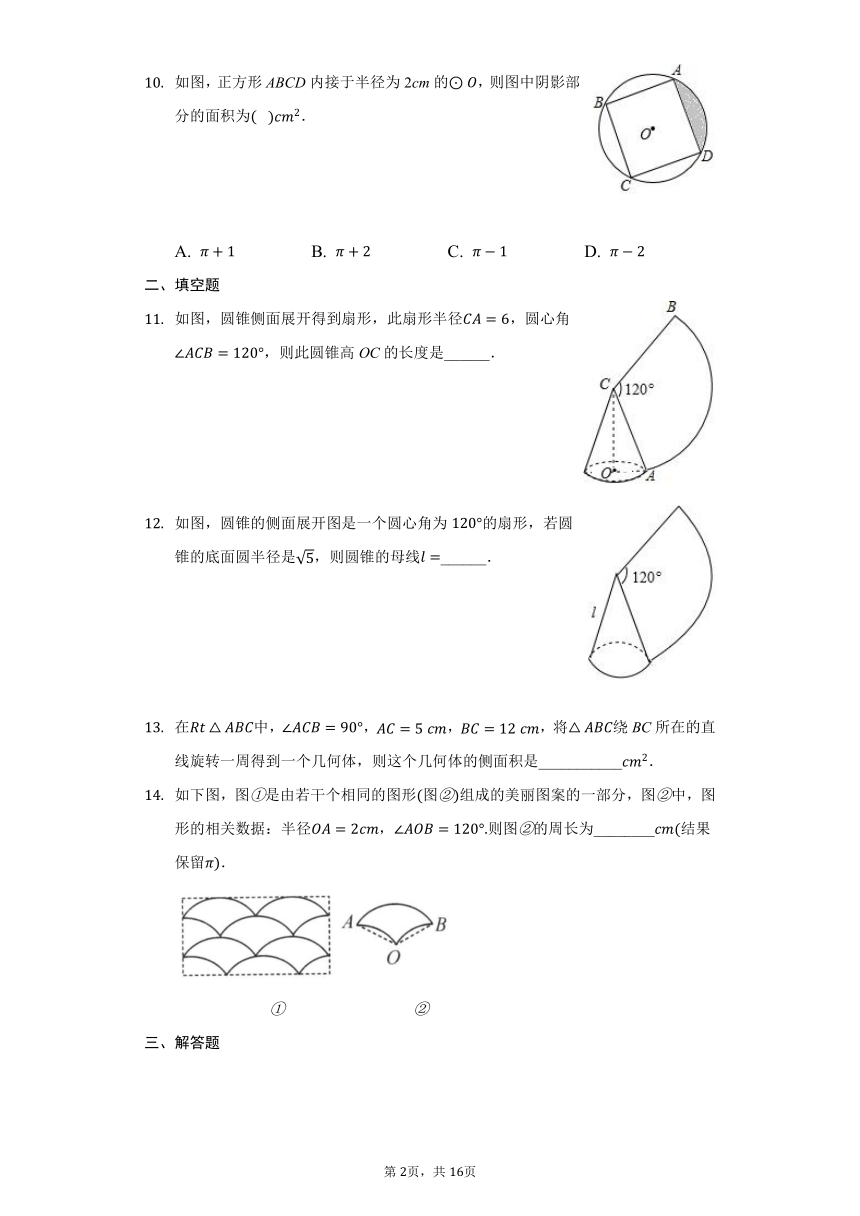
如图,正方形ABCD内接于半径为2cm的,则图中阴影部分的面积为?
.
A.
B.
C.
D.
二、填空题
如图,圆锥侧面展开得到扇形,此扇形半径,圆心角,则此圆锥高OC的长度是______.
如图,圆锥的侧面展开图是一个圆心角为的扇形,若圆锥的底面圆半径是,则圆锥的母线______.
在中,,,,将绕BC所在的直线旋转一周得到一个几何体,则这个几何体的侧面积是___________.
如下图,图是由若干个相同的图形图组成的美丽图案的一部分,图中,图形的相关数据:半径,则图的周长为________结果保留.
?
?
?
?
?
?
?
?
?
??
?
?
?
?
?
?
?
?
?
?
?
三、解答题
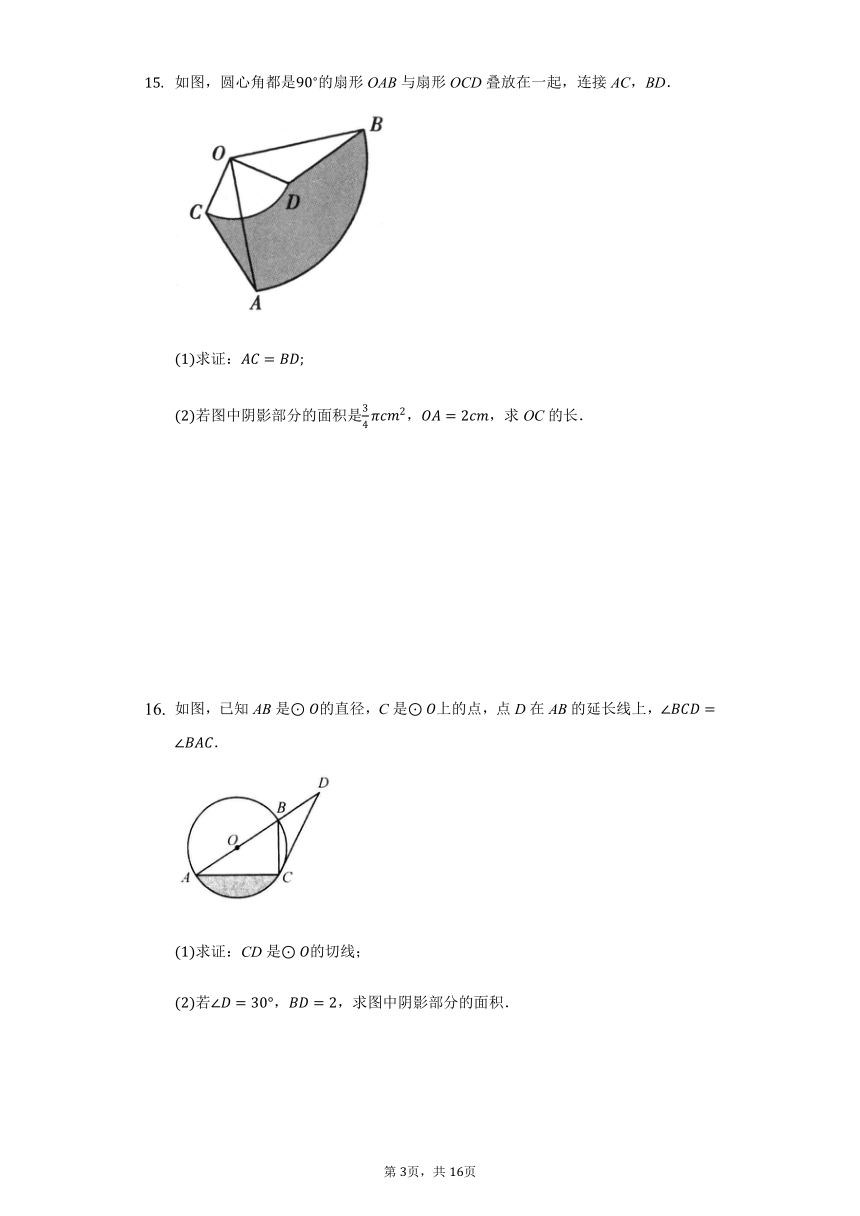
如图,圆心角都是的扇形OAB与扇形OCD叠放在一起,连接AC,BD.
求证:
若图中阴影部分的面积是,,求OC的长.
如图,已知AB是的直径,C是上的点,点D在AB的延长线上,.
求证:CD是的切线;
若,,求图中阴影部分的面积.
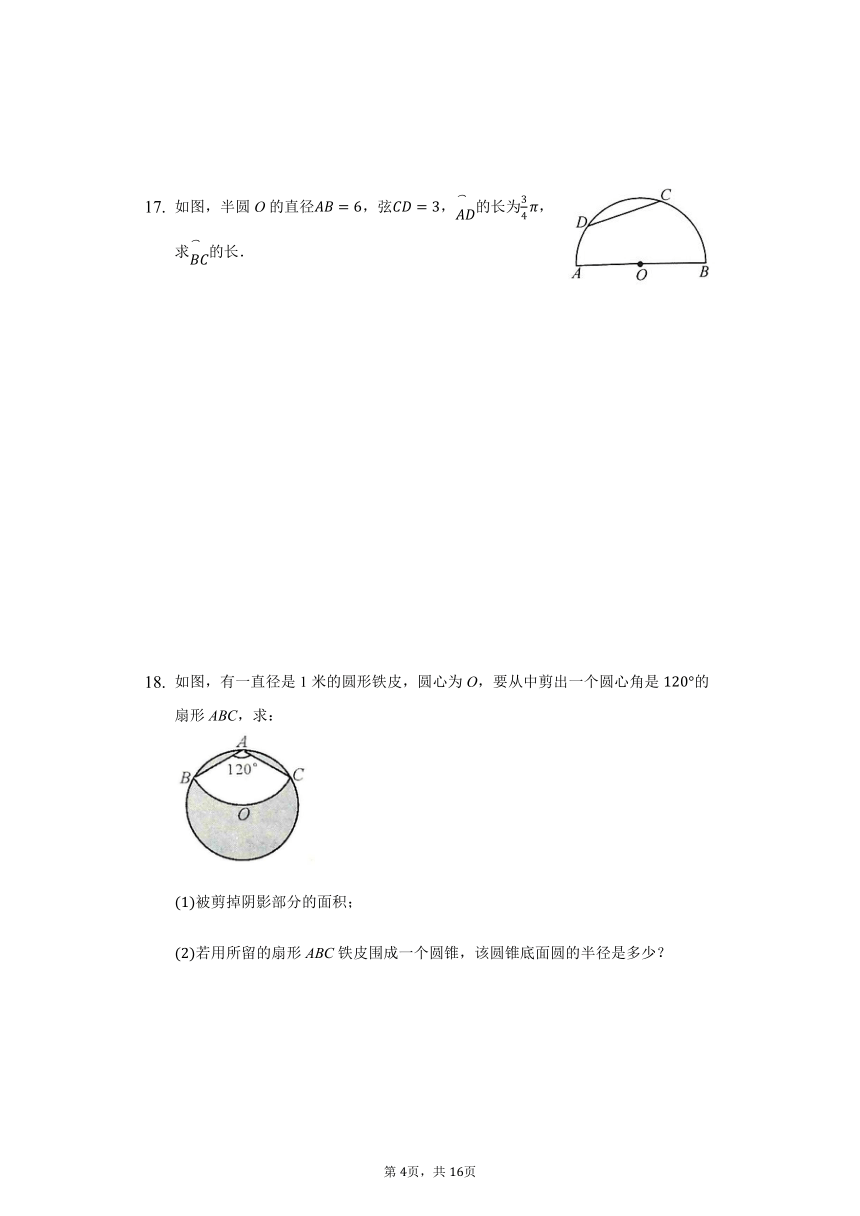
如图,半圆O的直径,弦,的长为,求的长.
如图,有一直径是1米的圆形铁皮,圆心为O,要从中剪出一个圆心角是的扇形ABC,求:
被剪掉阴影部分的面积;
若用所留的扇形ABC铁皮围成一个圆锥,该圆锥底面圆的半径是多少?
如下图,中,,D是边AB上一点,且.E是BC边上的一点,以EC为直径的经过点D.
求证:AB是的切线;
若,,求的长.
答案和解析
1.【答案】D
【解析】解:圆锥的底面周长为,
设侧面展开图的圆心角为n,
,
解得.
故选:D.
易得圆锥的底面周长,即为侧面展开图的弧长,利用弧长公式和母线长可得侧面展开图的圆心角.
本题考查了圆锥侧面圆心角的度数,用到的知识点为:圆锥的底面周长等于侧面展开图的弧长.
2.【答案】C
【解析】
【分析】
本题考查了弧长的计算,解答本题关键是熟练掌握弧长的计算公式,及公式字母表示的含义.
根据弧长公式:弧长为l,圆心角度数为n,圆的半径为,代入即可求出圆心角的度数.
【解答】
解:由题意得,,
解得:.
即这条弧所对的圆心角的度数是.
故选:C.
3.【答案】B
【解析】解:,
故选:B.
利用扇形的面积公式计算即可.
本题考查扇形的面积,解题的关键是记住扇形的面积公式.
4.【答案】A
【解析】解:设圆锥的底面圆半径为r,依题意,得
,
解得.
故小圆锥的底面半径为10.
故选:A.
圆锥的底面圆半径为r,根据圆锥的底面圆周长扇形的弧长,列方程求解.
本题考查了圆锥的计算.圆锥的侧面展开图为扇形,计算要体现两个转化:1、圆锥的母线长为扇形的半径,2、圆锥的底面圆周长为扇形的弧长.
5.【答案】A
【解析】
【分析】
本题考查了扇形的面积公式,正确理解公式是关键,从9点到9点30分分针扫过的扇形的圆心角是,利用扇形的面积公式即可求解.
【解答】
解:从9点到9点30分分针扫过的扇形的圆心角是,
则分针在钟面上扫过的面积是:
.
故选A.
6.【答案】B
【解析】
【分析】
本题考查了弧长的计算,掌握弧长公式是解题的关键.直接利用弧长公式即可求出n的值,计算即可.
【解答】
解:设此扇形的圆心角的度数为,
由弧长公式,得,解得,
即此扇形的圆心角的度数为.
故选B.
7.【答案】A
【解析】解:作,则,连接OA,OB,OC,
是BC的垂直平分线
,
,
在BC的垂直平分线上,
、O、D共线,
,,
,
,
,
,
是等边三角形,
,
,,
,
,
,
,
,
,
故选:A.
连接OB、OC,先利用同弧所对的圆周角等于所对的圆心角的一半,求出扇形的圆心角为60度,即可求出半径的长1,利用三角形和扇形的面积公式即可求解;
本题主要考查了扇形的面积公式,圆周角定理,垂径定理等,明确是解题的关键.
8.【答案】B
【解析】解:侧面积是:
故选:B.
底面周长与圆柱的高的乘积就是圆柱的侧面积.
本题考查了圆柱的计算,正确理解侧面积的计算方法是关键.
9.【答案】B
【解析】
【分析】
本题考查扇形面积的计算、圆周角定理,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
根据圆周角定理可以求得的度数,然后根据扇形面积公式即可解答本题.
【解答】
解:,
,
是的直径,CD是弦,,
阴影部分的面积是:,
故选:B.
10.【答案】D
【解析】
【分析】
本题考查正多边形与圆、正方形的性质、圆的面积公式、扇形的面积公式等知识,解题的关键是利用对称性可知阴影部分的面积等于圆的面积减去正方形的,也可以用扇形的面积减去三角形的面积计算,属于基础题.
根据对称性可知阴影部分的面积等于圆的面积减去正方形的,求出圆内接正方形的边长,即可求解.
【解答】
解:连接AO,DO,
是正方形,,
,
,
圆内接正方形的边长为,
所以阴影部分的面积.
故选D.
11.【答案】
【解析】
【分析】
此题主要考查了扇形的弧长公式,勾股定理,求出OA是解本题的关键.先根据圆锥的侧面展开图,扇形的弧长等于该圆锥的底面圆的周长,求出OA,最后用勾股定理即可得出结论.
【解答】
解:设圆锥底面圆的半径为r,
,,
,
,即:,
在中,,,根据勾股定理得,,
故答案为:.
12.【答案】
【解析】
【分析】
本题考查了圆锥的计算,用到的知识点为:圆锥的侧面展开图的弧长等于底面周长;弧长公式为:.
易得圆锥的底面周长,也就是侧面展开图的弧长,进而利用弧长公式即可求得圆锥的母线长.
【解答】
解:圆锥的底面周长,
则:,
解得.
故答案为:.
13.【答案】
【解析】解:在中,,,,
由勾股定理得,
圆锥的底面周长,
旋转体的侧面积,
故答案为:
易利用勾股定理求得母线长,那么圆锥的侧面积底面周长母线长.
本题考查圆锥的计算,关键是利用了勾股定理,圆的周长公式和扇形面积公式求解.
14.【答案】
【解析】
【分析】本题考查了弧长公式的计算,根据图形特点确定各弧之间的关系是本题的关键.
先根据图1确定:图2的周长个弧AB的长,根据弧长公式可得结论.
【解答】
解:由题图得的长的长的长,
半径,,
则题图的周长为.
故答案为.
15.【答案】证明:?,
,
.
在和中,
,
.
解:由知,
阴影部分的面积
,
,
.
【解析】本题考查了全等三角形的判定和性质、扇形面积的计算方法等知识点.
求证:,则需求证,利用已知条件证明即可.
从图中可以得就是大扇形减小扇形形所得的弓形的面积,根据扇形的面积公式计算即可.
16.【答案】解:连接OC,
,
,
,
,
是直径,
,
是半径,
是的切线
设的半径为r,
,
,,
,
,
,
,
由勾股定理可知:
易求
阴影部分面积为
【解析】本题考查圆的综合问题,涉及圆的切线判定,勾股定理,含30度的直角三角形的性质,等边三角形的性质等知识,需要学生灵活运用所学知识.
连接OC,易证,由于AB是直径,所以,所以,进而证明CD是的切线
设的半径为r,,由于,,所以可求出,,,由勾股定理可知:,分别计算的面积以及扇形OAC的面积即可求出阴影部分面积
17.【答案】解:连接OD、OC,
,
是等边三角形,
,
的长,
又半圆弧的长度为:,
.
【解析】本题考查圆了弧长的计算,等边三角形的判定与性质等知识,由题意可知:是等边三角形,从而可求出弧CD的长度,再求出半圆弧的长度后,即可求出弧BC的长度.
18.【答案】解:设O为圆心,连接OA、OB,OC,BC,且OA与BC交于点D,如图所示:
在和中,
,
≌,
又,
,
又,
是等边三角形,
米,
,
;
弧BC的长,
设圆锥的底面半径为r,
,
,
圆锥底面圆的半径是
【解析】本题考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.设O为圆心,连接OA,OB,OC,BC,由,且,从而得出三角形ABO与三角形ACO全等,可得,先求得圆的面积,再求得扇形的面积,求差即可;
求得扇形的弧长,即为圆锥底面圆的周长,从而得出圆锥底面圆的半径.
19.【答案】证明:连接OD,如图所示:
,
,
又为的外角,
,
又,
,
,
,
,
,
,
是的切线;
解:,
,
,
,
,
,
,
,
,
的长.
【解析】连接OD,由,根据等边对等角得到一对角相等,再由为的外角,利用三角形的外角等于与它不相邻的两个内角之和,等量代换可得出,又,可得出,又,可得出直角三角形ABC中两锐角互余,等量代换可得出与互余,即OD垂直于BD,确定出AB为圆O的切线,得证;
由已知得到,根据直角三角形的性质得到,求得,根据勾股定理得到,根据弧长公式即可得到结论.
此题考查了切线的性质,垂径定理,勾股定理,三角形的外角性质等,熟练掌握定理及性质是解本题的关键.
第2页,共2页
第1页,共1页
一、选择题
若圆锥的底面半径为3,母线长为5,则它的侧面展开图的圆心角等于
A.
B.
C.
D.
有一条弧的长为,半径为2cm,则这条弧所对的圆心角的度数是
A.
B.
C.
D.
已知扇形的圆心角为,半径长为3,则该扇形的面积为
A.
B.
C.
D.
用一个半径为30,圆心角为的扇形围成一个圆锥,则这个圆锥的底面半径是
A.
10
B.
20
C.
D.
钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是.
A.
B.
C.
D.
已知扇形的半径为3,弧长为,则此扇形的圆心角的度数为
A.
B.
C.
D.
如图,在中,,,,则阴影部分的面积是???
A.
B.
C.
D.
圆柱形水桶的底面周长为,高为,它的侧面积是
A.
B.
C.
D.
如图,AB是的直径,CD是弦,,,则阴影部分的面积是
A.
B.
C.
D.
如图,正方形ABCD内接于半径为2cm的,则图中阴影部分的面积为?
.
A.
B.
C.
D.
二、填空题
如图,圆锥侧面展开得到扇形,此扇形半径,圆心角,则此圆锥高OC的长度是______.
如图,圆锥的侧面展开图是一个圆心角为的扇形,若圆锥的底面圆半径是,则圆锥的母线______.
在中,,,,将绕BC所在的直线旋转一周得到一个几何体,则这个几何体的侧面积是___________.
如下图,图是由若干个相同的图形图组成的美丽图案的一部分,图中,图形的相关数据:半径,则图的周长为________结果保留.
?
?
?
?
?
?
?
?
?
??
?
?
?
?
?
?
?
?
?
?
?
三、解答题
如图,圆心角都是的扇形OAB与扇形OCD叠放在一起,连接AC,BD.
求证:
若图中阴影部分的面积是,,求OC的长.
如图,已知AB是的直径,C是上的点,点D在AB的延长线上,.
求证:CD是的切线;
若,,求图中阴影部分的面积.
如图,半圆O的直径,弦,的长为,求的长.
如图,有一直径是1米的圆形铁皮,圆心为O,要从中剪出一个圆心角是的扇形ABC,求:
被剪掉阴影部分的面积;
若用所留的扇形ABC铁皮围成一个圆锥,该圆锥底面圆的半径是多少?
如下图,中,,D是边AB上一点,且.E是BC边上的一点,以EC为直径的经过点D.
求证:AB是的切线;
若,,求的长.
答案和解析
1.【答案】D
【解析】解:圆锥的底面周长为,
设侧面展开图的圆心角为n,
,
解得.
故选:D.
易得圆锥的底面周长,即为侧面展开图的弧长,利用弧长公式和母线长可得侧面展开图的圆心角.
本题考查了圆锥侧面圆心角的度数,用到的知识点为:圆锥的底面周长等于侧面展开图的弧长.
2.【答案】C
【解析】
【分析】
本题考查了弧长的计算,解答本题关键是熟练掌握弧长的计算公式,及公式字母表示的含义.
根据弧长公式:弧长为l,圆心角度数为n,圆的半径为,代入即可求出圆心角的度数.
【解答】
解:由题意得,,
解得:.
即这条弧所对的圆心角的度数是.
故选:C.
3.【答案】B
【解析】解:,
故选:B.
利用扇形的面积公式计算即可.
本题考查扇形的面积,解题的关键是记住扇形的面积公式.
4.【答案】A
【解析】解:设圆锥的底面圆半径为r,依题意,得
,
解得.
故小圆锥的底面半径为10.
故选:A.
圆锥的底面圆半径为r,根据圆锥的底面圆周长扇形的弧长,列方程求解.
本题考查了圆锥的计算.圆锥的侧面展开图为扇形,计算要体现两个转化:1、圆锥的母线长为扇形的半径,2、圆锥的底面圆周长为扇形的弧长.
5.【答案】A
【解析】
【分析】
本题考查了扇形的面积公式,正确理解公式是关键,从9点到9点30分分针扫过的扇形的圆心角是,利用扇形的面积公式即可求解.
【解答】
解:从9点到9点30分分针扫过的扇形的圆心角是,
则分针在钟面上扫过的面积是:
.
故选A.
6.【答案】B
【解析】
【分析】
本题考查了弧长的计算,掌握弧长公式是解题的关键.直接利用弧长公式即可求出n的值,计算即可.
【解答】
解:设此扇形的圆心角的度数为,
由弧长公式,得,解得,
即此扇形的圆心角的度数为.
故选B.
7.【答案】A
【解析】解:作,则,连接OA,OB,OC,
是BC的垂直平分线
,
,
在BC的垂直平分线上,
、O、D共线,
,,
,
,
,
,
是等边三角形,
,
,,
,
,
,
,
,
,
故选:A.
连接OB、OC,先利用同弧所对的圆周角等于所对的圆心角的一半,求出扇形的圆心角为60度,即可求出半径的长1,利用三角形和扇形的面积公式即可求解;
本题主要考查了扇形的面积公式,圆周角定理,垂径定理等,明确是解题的关键.
8.【答案】B
【解析】解:侧面积是:
故选:B.
底面周长与圆柱的高的乘积就是圆柱的侧面积.
本题考查了圆柱的计算,正确理解侧面积的计算方法是关键.
9.【答案】B
【解析】
【分析】
本题考查扇形面积的计算、圆周角定理,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
根据圆周角定理可以求得的度数,然后根据扇形面积公式即可解答本题.
【解答】
解:,
,
是的直径,CD是弦,,
阴影部分的面积是:,
故选:B.
10.【答案】D
【解析】
【分析】
本题考查正多边形与圆、正方形的性质、圆的面积公式、扇形的面积公式等知识,解题的关键是利用对称性可知阴影部分的面积等于圆的面积减去正方形的,也可以用扇形的面积减去三角形的面积计算,属于基础题.
根据对称性可知阴影部分的面积等于圆的面积减去正方形的,求出圆内接正方形的边长,即可求解.
【解答】
解:连接AO,DO,
是正方形,,
,
,
圆内接正方形的边长为,
所以阴影部分的面积.
故选D.
11.【答案】
【解析】
【分析】
此题主要考查了扇形的弧长公式,勾股定理,求出OA是解本题的关键.先根据圆锥的侧面展开图,扇形的弧长等于该圆锥的底面圆的周长,求出OA,最后用勾股定理即可得出结论.
【解答】
解:设圆锥底面圆的半径为r,
,,
,
,即:,
在中,,,根据勾股定理得,,
故答案为:.
12.【答案】
【解析】
【分析】
本题考查了圆锥的计算,用到的知识点为:圆锥的侧面展开图的弧长等于底面周长;弧长公式为:.
易得圆锥的底面周长,也就是侧面展开图的弧长,进而利用弧长公式即可求得圆锥的母线长.
【解答】
解:圆锥的底面周长,
则:,
解得.
故答案为:.
13.【答案】
【解析】解:在中,,,,
由勾股定理得,
圆锥的底面周长,
旋转体的侧面积,
故答案为:
易利用勾股定理求得母线长,那么圆锥的侧面积底面周长母线长.
本题考查圆锥的计算,关键是利用了勾股定理,圆的周长公式和扇形面积公式求解.
14.【答案】
【解析】
【分析】本题考查了弧长公式的计算,根据图形特点确定各弧之间的关系是本题的关键.
先根据图1确定:图2的周长个弧AB的长,根据弧长公式可得结论.
【解答】
解:由题图得的长的长的长,
半径,,
则题图的周长为.
故答案为.
15.【答案】证明:?,
,
.
在和中,
,
.
解:由知,
阴影部分的面积
,
,
.
【解析】本题考查了全等三角形的判定和性质、扇形面积的计算方法等知识点.
求证:,则需求证,利用已知条件证明即可.
从图中可以得就是大扇形减小扇形形所得的弓形的面积,根据扇形的面积公式计算即可.
16.【答案】解:连接OC,
,
,
,
,
是直径,
,
是半径,
是的切线
设的半径为r,
,
,,
,
,
,
,
由勾股定理可知:
易求
阴影部分面积为
【解析】本题考查圆的综合问题,涉及圆的切线判定,勾股定理,含30度的直角三角形的性质,等边三角形的性质等知识,需要学生灵活运用所学知识.
连接OC,易证,由于AB是直径,所以,所以,进而证明CD是的切线
设的半径为r,,由于,,所以可求出,,,由勾股定理可知:,分别计算的面积以及扇形OAC的面积即可求出阴影部分面积
17.【答案】解:连接OD、OC,
,
是等边三角形,
,
的长,
又半圆弧的长度为:,
.
【解析】本题考查圆了弧长的计算,等边三角形的判定与性质等知识,由题意可知:是等边三角形,从而可求出弧CD的长度,再求出半圆弧的长度后,即可求出弧BC的长度.
18.【答案】解:设O为圆心,连接OA、OB,OC,BC,且OA与BC交于点D,如图所示:
在和中,
,
≌,
又,
,
又,
是等边三角形,
米,
,
;
弧BC的长,
设圆锥的底面半径为r,
,
,
圆锥底面圆的半径是
【解析】本题考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.设O为圆心,连接OA,OB,OC,BC,由,且,从而得出三角形ABO与三角形ACO全等,可得,先求得圆的面积,再求得扇形的面积,求差即可;
求得扇形的弧长,即为圆锥底面圆的周长,从而得出圆锥底面圆的半径.
19.【答案】证明:连接OD,如图所示:
,
,
又为的外角,
,
又,
,
,
,
,
,
,
是的切线;
解:,
,
,
,
,
,
,
,
,
的长.
【解析】连接OD,由,根据等边对等角得到一对角相等,再由为的外角,利用三角形的外角等于与它不相邻的两个内角之和,等量代换可得出,又,可得出,又,可得出直角三角形ABC中两锐角互余,等量代换可得出与互余,即OD垂直于BD,确定出AB为圆O的切线,得证;
由已知得到,根据直角三角形的性质得到,求得,根据勾股定理得到,根据弧长公式即可得到结论.
此题考查了切线的性质,垂径定理,勾股定理,三角形的外角性质等,熟练掌握定理及性质是解本题的关键.
第2页,共2页
第1页,共1页
同课章节目录
