北师大版八年级数学上册 4.2 一4.4测试题(2课时 Word版 含解析)
文档属性
| 名称 | 北师大版八年级数学上册 4.2 一4.4测试题(2课时 Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 726.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 00:00:00 | ||
图片预览




文档简介
4.2 一次函数与正比例函数
一.选择题
1.在①y=﹣8x;②y=﹣;③y=+1;④y=﹣8x2+6;⑤y=﹣0.5x﹣1中,一次函数有( )
A.1个 B.2个 C.3个 D.4个
2.下列关系式中,一次函数是( )
A.y=﹣1 B.y=x2+3
C.y=k+b(k、b是常数) D.y=3x
3.函数①y=πx;②y=2x﹣1;③y=,④y=x2﹣1中,y是x的一次函数的有( )
A.1个 B.2个 C.3个 D.4个
4.下列函数中:①y=﹣x;②y=;③y=;④y=2x+1,其中一次函数的个数是( )
A.1 B.2 C.3 D.4
5.下列函数中,y是x的一次函数的是( )
A.y=x2+2x B. C.y=x D.
6.若函数y=(m﹣1)x+3是一次函数,则m的值为( )
A.﹣1 B.1 C.0 D.﹣1或1
7.下列函数中,是一次函数的有( )
A. B.y=3x+1
C. D.y=ax﹣2(a为常数)
8.若函数y=(m﹣1)x|m|是正比例函数,则m的值为( )
A.1 B.﹣1 C.±1 D.2
9.下列函数中,正比例函数是( )
A.y=﹣3x+1 B.y=﹣ C.y=﹣x2+3 D.y=﹣
10.下列函数中,正比例函数是( )
A.y=﹣8x B.y= C.y=x2 D.y=8x﹣4
11.已知函数y=(2﹣m)x|m﹣1|是正比例函数,则m的值是( )
A.1 B.2或0 C.2 D.0
12.一次函数y=kx﹣b的图象如图所示,则关于x的方程kx﹣b=0的解是( )
A.(1,0) B.(0,﹣1) C.x=1 D.x=﹣1
13.一次函数y=kx+b的图象如图所示,则关于x的方程kx+b=﹣2的解为( )
A.x=0 B.x=﹣1 C.x=2 D.x=﹣2
14.已知一次函数y=kx+b的图象如图所示,则关于x的方程kx+b=0的解为( )
A.x=3 B.x=1.5 C.x=﹣3 D.x=﹣1.5
15.若一次函数y=x+n(n为常数)的图象如图所示,则关于x的一元一次方程x+n=0的解为( )
A.x=0 B. C.x=1 D.x=2
二.填空题
16.在一次函数y=﹣2(x+1)+x中,k为 ,b为 .
17.当m= 时,函数y=(m+1)x+5是一次函数.
18.已知y=(m﹣1)x﹣1是关于x的一次函数,则m为 .
19.已知一次函数y=(m﹣1)x|m|﹣2,则m= .
20.若y=(k﹣1)x2﹣|k|+k+1是关于x的正比例函数,则k= .
21.如果函数y=(m﹣)x是正比例函数,那么m= .
22.若y=(m﹣2)x+5是一次函数函数,则其解析式为 .
23.已知y﹣2与x+3成正比,且当x=1时,y=﹣6,则y与x的关系式是 .
24.若函数是正比例函数,则该函数表达式是 .
25.一次函数y=kx+b的图象如图所示,则关于x的方程kx+b=﹣1的解为 .
三.解答题
26.当k为何值时,函数y=(k+3)xk+1+4x﹣8(x≠0)是一次函数?
27.已知,直线L经过点A(4,0),B(0,2).
(1)画出直线L的图象,并求出直线L的解析式;
(2)求S△AOB;
(3)在x轴上是否存在一点P,使S△PAB=3?若存在,求出点P的坐标,若不存在,请说明理由.
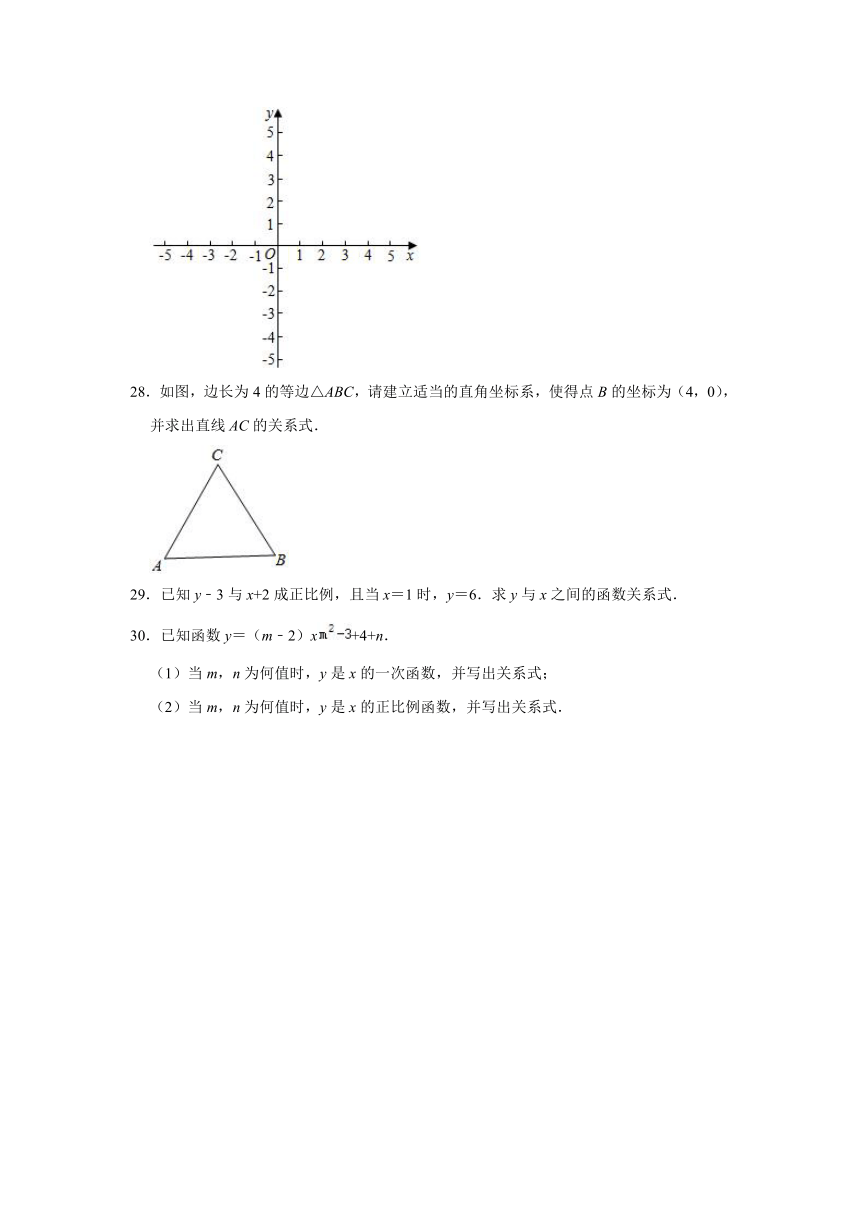
28.如图,边长为4的等边△ABC,请建立适当的直角坐标系,使得点B的坐标为(4,0),并求出直线AC的关系式.
29.已知y﹣3与x+2成正比例,且当x=1时,y=6.求y与x之间的函数关系式.
30.已知函数y=(m﹣2)x+4+n.
(1)当m,n为何值时,y是x的一次函数,并写出关系式;
(2)当m,n为何值时,y是x的正比例函数,并写出关系式.
参考答案
一.选择题
1.解:①y=﹣8x属于一次函数;
②y=﹣属于反比例函数;
③y=+1不属于一次函数;
④y=﹣8x2+6属于二次函数;
⑤y=﹣0.5x﹣1属于一次函数,
∴一次函数有2个,
故选:B.
2.解:A、自变量在分母上,不符合一次函数定义,故此选项不符合题意;
B、y=x2+3是二次函数,不是一次函数,故此选项不符合题意;
C、少x,不符合一次函数定义,故此选项不符合题意;
D、y=3x是正比例函数也是一次函数,故此选项符合题意;
故选:D.
3.解:①y=πx;②y=2x﹣1是一次函数;
③y=是反比例函数,不是一次函数;
④y=x2﹣1是二次函数,不是一次函数,
因此一次函数共2个,
故选:B.
4.解:①y=﹣x;②y=;④y=2x+1是一次函数,共3个,
故选:C.
5.解:A.y=x2+2x属于二次函数,不合题意;
B.y=属于反比例函数,不合题意;
C.y=x属于一次函数,符合题意;
D.y=+1不是一次函数,不合题意;
故选:C.
6.解:由题意得:m2=1,且m﹣1≠0,
解得:m=﹣1,
故选:A.
7.解:A、y=x2不符合一次函数的定义,故此选项不合题意;
B、y=3x+1属于一次函数,故此选项符合题意;
C、y=不符合一次函数的定义,故此选项不合题意;
D、y=ax﹣2不符合一次函数的定义,故此选项不合题意;
故选:B.
8.解:由题意得:m﹣1≠0,|m|=1,
解得:m=﹣1.
故选:B.
9.解:A.是一次函数,不是正比例函数,故本选项不符合题意;
B.是正比例函数,故本选项符合题意;
C.是二次函数,不是正比例函数,故本选项不符合题意;
D.是反比例函数,不是正比例函数,故本选项不符合题意;
故选:B.
10.解:A、是正比例函数,故此选项符合题意;
B、是反比例函数,不是正比例函数,故此选项不合题意;
C、是二次函数,不是正比例函数,故此选项不合题意;
D、是一次函数,不是正比例函数,故此选项不合题意;
故选:A.
11.解:∵函数y=(2﹣m)x|m﹣1|是正比例函数,
∴|m﹣1|=1,且2﹣m≠0,
∴m﹣1=±1,且m≠2,
解得m=0.
故选:D.
12.解:从图象知,函数y=kx﹣b的图象经过点(1,0),
∴关于x的方程kx﹣b=0的解是x=1.
故选:C.
13.解:∵从图象可知:一次函数y=kx+b的图象与直线y=﹣2的交点坐标为(﹣1,﹣2),
∴关于x的方程kx+b=﹣2的解为x=﹣1,
故选:B.
14.解:由一次函数y=kx+b的图象可得y=0时,x=1.5,
因此关于x的方程kx+b=0的解为x=1.5,
故选:B.
15.解:由一次函数y=x+n的图象可得:当y=0时,x=2,
因此一元一次方程x+n=0的解为x=2,
故选:D.
二.填空题
16.解:∵y=﹣2(x+1)+x,
∴y=﹣x﹣2,
∴k=﹣1,b=﹣2.
故答案为:﹣1;﹣2.
17.解:根据一次函数的定义,可知:m2=1,m+1≠0,
解得:m=±1且m≠﹣1,
∴m=1.
故答案为:1.
18.解:由题意得:m2=1,且m﹣1≠0,
解得:m=﹣1,
故答案为:﹣1.
19.解:∵y=(m﹣1)x|m|﹣2是一次函数,
∴|m|=1,m﹣1≠0,
解得m=﹣1.
故答案为:﹣1.
20.解:∵y=(k﹣1)x2﹣|k|+k+1,y是x的正比例函数,
∴2﹣|k|=1,且k﹣1≠0,k+1=0,
解得:k=﹣1.
故答案为:﹣1.
21.解:∵函数y=(m﹣)x是正比例函数,
∴m﹣0且m2﹣1=1,
解得:m=﹣,
故答案为:﹣.
22.解:∵y=(m﹣2)x+5是一次函数函数,
∴m﹣2≠0,且m2﹣3=1,
解得:m=﹣2,
∴y=﹣4x+5,
故答案为y=﹣4x+5.
23.解:设y﹣2=k(x+3),
根据题意得:﹣6﹣2=4k,
则k=﹣2,
则函数的解析式是:y=﹣2x﹣6.
故答案为y=﹣2x﹣6.
24.解:∵是正比例函数,
∴,
解得:m=﹣2,
该函数表达式是y=﹣4x,
故答案为:y=﹣4x.
25.解:∵一次函数y=kx+b的图象过点(,﹣1),
∴关于x的方程kx+b=﹣1的解是x=,
故答案为:x=.
三.解答题
26.解:∵y=(k+3)xk+1+4x﹣8(x≠0),
∴k+1=1,k+3+4≠0,
解得:k=0.
∴当k为0时,函数y=(k+3)xk+1+4x﹣8(x≠0)是一次函数.
27.解:(1)画出函数图象如图:
设直线l的解析式为y=kx+b,
把A(4,0)、点B(0,2)分别代入得,解得,
∴一次函数解析式为y=﹣x+2;
(2)∵点A(4,0),B(0,2).
∴OA=4,OB=2,
∴S△AOB==4;
(3)在x轴上存在一点P,使S△PAB=3,理由如下:
设P(x,0),
∵A(4,0)、B(0,2),
∴PA=|x﹣4|,
∵S△PAB=3,
∴PA?OB=3,即|x﹣4|×2=3,
∴x﹣4=±3,
∴x=7或1,
∴P的坐标为(7,0)或(1,0).
28.解:以A为原点,AB所在直线为x轴建立直角坐标系,
此时A、B点的坐标分别为(0,0)、(4,0),
作CD⊥AB于D,则AD=BD=AB=2.
∴CD===2,
∴C(2,2),
设直线AC的解析式为y=kx,
把C(2,2)代入得,2=2k,
解得k=,
∴直线AC的关系式为y=x.
29.解:设y﹣3=k(x+2)(k≠0).
∵当x=1时,y=6,
∴k(1+2)=6﹣3,
解得 k=1,
所以y与x之间的函数关系式为:y=x+5.
30.解:(1)根据题意得,,
解得m=﹣2,
故当m=﹣2,n为任意实数时,y是x的一次函数,解析式为y=﹣4x+4+n,
(2)根据题意得,
解得m=﹣2,n=﹣4,
故m=﹣2,n=﹣4时,y是x的正比例函数,解析式为y=﹣4x.
4.3 一次函数的图象
一.选择题
1.在同一直角坐标系中,一次函数y=kx+b和y=bx+k的图象可能正确的是( )
A. B.
C. D.
2.下面所画的函数图象中,不可能是一次函数y=mx+2﹣m图象的是( )
A. B.
C. D.
3.一次函数y1=kx+b与y2=bx+k(k,b为常数)在同一平面直角坐标系中大致图象可能是( )
A. B.
C. D.
4.下列图形中,表示一次函数y=mx+n与正比例函数y=﹣mnx(m,n为常数,且mn≠0)的图象不正确的是( )
A. B.
C. D.
5.若正比例函数y=kx的图象如图所示,则一次函数y=﹣kx+k的图象大致是( )
A. B.
C. D.
6.点P1(x1,y1),点P2(x2,y2)是一次函数y=4x+3图象上的两个点,且x1<x2,则y1与y2的大小关系是( )
A.y1>y2 B.y1>y2>0 C.y1<y2 D.y1=y2
7.一次函数y=mx﹣n与y=mnx(mn≠0),在同一平面直角坐标系的图象不可能是( )
A. B.
C. D.
8.若a,b为实数,且++b=3,则直线y=ax﹣b不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.已知关于x的多项式x2+kx+1是一个完全平方式,则一次函数y=(k﹣2)x+5经过的象限是( )
A.第一、二、三象限 B.第二、三、四象限
C.第一、二、四象限 D.第一、三、四象限
10.如图,平面直角坐标系xOy中,阴影部分(射线y=x,x>0与y正半轴之间,不含边界)的点的坐标(x,y)满足( )
A.x=y B.x>y>0 C.y>x>0 D.y=x>0
11.下列一次函数中,y随x值的增大而减小的( )
A.y=2x+1 B.y=3﹣4x C.y=πx+2 D.y=(5﹣2)x
12.在一次函数y=(k﹣1)x的图象上,y都随x的增大而增大,则k的值可以是( )
A.﹣1 B.0 C.1 D.2
13.一次函数y=(m﹣1)x+3,y随x的增大而增大,则m的值可以为( )
A.0 B.1 C.2 D.﹣2
14.若点P在一次函数y=x﹣4的图象上,则点P一定不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
15.对于函数y=﹣3x+1,下列结论正确的是( )
A.它的图象必经过点(1,3)
B.y的值随x值的增大而增大
C.当x>0时,y<0
D.它的图象不经过第三象限
二.填空题
16.若点P(﹣1,y1)和点Q(﹣2,y2)是一次函数y=﹣x+b的图象上的两点,则y1,y2的大小关系是:y1 y2(填“>,<或=”).
17.直线ax+y﹣2a+1=0与直线(a+2)x﹣ay+3=0垂直,则a的值为 .
18.复习课中,教师给出关于x的函数y=﹣2mx+m﹣1(m≠0),学生们在独立思考后,给出了5条关于这个函数的结论:
①此函数是一次函数,但不可能是正比例函数;
②函数的值y随着自变量x的增大而减小;
③该函数图象与y轴的交点在y轴的正半轴上;
④若函数图象与x轴交于A(a,0),则a<0.5;
⑤此函数图象与直线y=4x﹣3,y轴成的面积必小于0.5.
对于以上5个结论正确有 个.
19.正比例函数y=﹣的图象经过第 象限.
20.已知正比例函数y=(1+)x,y随着x的增大而增大,则k的取值范围是 .
21.有一种动画设计,屏幕上的△ABC是黑色区域(含三角形的边界).其中A(﹣1,1),B(2,1),C(1,3).用信号枪沿直线y=kx﹣2发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的k的取值范围是 .
22.如图,平面直角坐标系中,直线y=﹣x+1与x轴、y轴分别交于点A、B,点P与点O关于直线AB对称,则点P的坐标为 .
23.如图,直线y=x+3与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为 .
24.如图,将直线OA向上平移2个单位长度,则平移后的直线的表达式为 .
25.要把直线y=3x﹣2向上平移,使其图象经过点(2,10),需要向上平移 个单位.
三.解答题
26.画出下列正比例函数和一次函数的图象:
(1)y=2x;
(2)y=﹣2x﹣4.
27.(1)在平面直角坐标系中,作出y=2x﹣2的图象.
(2)根据图象,直接写出y>0时自变量x的取值范围.
28.已知一次函数y=(2m+1)x+3+m.
(1)若y随x的增大而减小,求m的取值范围;
(2)若图象经过点(﹣1,1),求m的值,画出这个函数图象.
29.对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1﹣x2|+|y1﹣y2|叫做P1,P2两点间的直角距离,记作d(P1,P2).
(1)已知A(1,1),B(5,4),求d(A,B).
(2)已知点O为坐标原点,动点P(x,y)满足d(O,P)=2,请写出y与x之间的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形.
(3)设点P0(x0,y0)是一定点,点Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做点P0到直线y=ax+b的直角距离.试求点M(1,﹣3)到直线y=x+2的直角距离.
30.已知正比例函数的图象经过点A(2,3);
(1)求出此正比例函数表达式;
(2)该直线向上平移3个单位,写出平移后所得直线的表达式,并画出它的图象.
参考答案
一.选择题
1.解:A、一条直线反映k>0,b>0,一条直线反映k>0,b<0,故本选项错误;
B、一条直线反映出k>0,b<0,一条直线反映k>0,b<0,一致,故本选项正确;
C、一条直线反映k<0,b>0,一条直线反映k>0,b<0,故本选项错误;
D、一条直线反映k>0,b<0,一条直线反映k<0,b<0,故本选项错误.
故选:B.
2.解:根据图象知:
A、m<0,2﹣m>0.解得m<0,所以有可能;
B、m>0,2﹣m>0.解得0<m<2,所以有可能;
C、m<0,2﹣m<0.两不等式无公共部分,所以不可能;
D、m>0,2﹣m<0.解得m>2,所以有可能.
故选:C.
3.解:A、直线y1=kx+b反映k>0,b<0,直线y2=bx+k反映k>0,b>0,故本选项错误;
B、直线y1=kx+b反映k<0,b<0,直线y2=bx+k反映k>0,b<0,故本选项错误;
C、直线y1=kx+b反映k>0,b<0,直线y2=bx+k反映k<0,b<0,故本选项错误;
D、直线y1=kx+b反映k<0,b>0,直线y2=bx+k反映k<0,b>0,一致,故本选项正确.
故选:D.
4.解:①当﹣mn<0,m,n同号,同正时y=mx+n过一、二、三象限,同负时过二、三、四象限;
②当﹣mn>0时,m,n异号,则y=mx+n过一、三、四象限或一、二、四象限.
故选:B.
5.解:∵正比例函数y=kx的图象经过第二、四象限,
∴k<0,
∴﹣k>0,
∴y=﹣kx+k的图象经过一、三、四象限,
故选:D.
6.解:∵k=4>0,
∴y随x的增大而增大,
又∵x1<x2,
∴y1<y2.
故选:C.
7.解:当m>0,n>0时,一次函数y=mx﹣n的图象经过第一、三、四象限,一次函数y=mnx的图象经过第一、三象限,故选项B正确,选项C错误;
当m>0,n<0时,一次函数y=mx﹣n的图象经过第一、二、三象限,一次函数y=mnx的图象经过第二、四象限,故选项A正确;
当m<0,n<0时,一次函数y=mx﹣n的图象经过第一、二、四象限,一次函数y=mnx的图象经过第一、三象限,故选项D正确;
故选:C.
8.解:∵++b=3,
∴,
解得a=,
∴+b=3,
∴b=3,
∴直线y=x﹣3,该直线经过第一、三、四象限,不经过第二象限,
故选:B.
9.解:∵关于x的多项式x2+kx+1是一个完全平方式,
∴k=±2,
当k=2时,函数y=(2﹣2)x+5=5是常数函数,不是一次函数;
当k=﹣2时,一次函数y=(﹣2﹣2)x+5=﹣4x+5,则该函数经过第一、二、四象限,
故选:C.
10.解:当x=y>0时在射线y=x上,
故当y>x>0时点(x,y)在阴影部分内,
故选:C.
11.解:A、∵k=2>0,
∴y随x值的增大而增大;
B、∵k=﹣4<0,
∴y随x值的增大而减少;
C、∵k=π>0,
∴y随x值的增大而增大;
D、∵k=5﹣2=3>0,
∴y随x值的增大而增大.
故选:B.
12.解:∵一次函数y=(k﹣1)x的图象中,y随x的增大而增大,
∴k﹣1>0,解得k>1,
∴k可以取2.
故选:D.
13.解:∵一次函数y=(m﹣1)x+3,若y随x的增大而增大,
∴m﹣1>0,解得m>1,
只有2合适,
故选:C.
14.解:∵k=1>0,b=﹣4<0,
∴一次函数y=x﹣4的图象经过第一、三、四象限,
又∵点P在一次函数y=x﹣4的图象上,
∴点P一定不在第二象限.
故选:B.
15.解:A、当x=1时,y=﹣3×1+1=﹣2,
∴点(1,﹣2)在函数y=﹣3x+1的图象,结论A不正确;
B、∵k=﹣3<0,
∴y随x的增大而减小,结论B不正确;
C、当y=0时,﹣3x+1=0,解得:x=,
∴当0<x<时,y>0,结论C不正确;
D、∵k=﹣3<0,b=1>0,
∴函数y=﹣3x+1的图象经过第一、二、四象限,
∴函数y=﹣3x+1的图象不经过第三象限,结论D正确.
故选:D.
二.填空题
16.解:∵k=﹣1<0,
∴y随x的增大而减小,
又∵﹣1>﹣2,
∴y1<y2.
故答案为:<.
17.解:当a=0时,直线ax+y﹣2a+1=0可以写成直线y=﹣1,直线(a+2)x﹣ay+3=0可以写成x=﹣,此时直线ax+y﹣2a+1=0与直线(a+2)x﹣ay+3=0垂直;
当a≠0时,直线ax+y﹣2a+1=0可以写成直线y=﹣ax+2a﹣1,直线(a+2)x﹣ay+3=0可以写成直线y=x+,
∵直线ax+y﹣2a+1=0与直线(a+2)x﹣ay+3=0垂直,
∴﹣a=﹣1,
解得a=﹣1;
故答案为:0或﹣1.
18.解:此函数是一次函数,当m=1时,它是正比例函数,所以①错误;
当m<0时,函数的值y 随着自变量x的增大而增大,所以②错误;
当m<1时,该函数图象与y轴的交点在y轴的负半轴上,所以③错误;
若函数图象与x轴交于A(a,0),则﹣2ma+m﹣1=0,解得a==0.5﹣,当m>0时,a<0.5,当m<0时,a>0.5,所以④错误;
此函数图象与直线y=4x﹣3的交点坐标为(,﹣1),此直线与y轴的交点坐标为(0,m﹣1),直线y=4x﹣3与y轴的交点坐标为(0,﹣3),所以此函数图象与直线y=4x﹣3、y轴围成的面积=?|m﹣1+3|?=?|m+2|,当m=2时,面积为1,所以⑤错误.
故答案为:0.
19.解:由正比例函数y=﹣中的k=﹣,知函数y=﹣的图象经过第二、四象限.
故答案是:二、四.
20.解:∵正比例函数y=(1+)x中,y随x的增大而增大,
∴1+>0,
即k>﹣5.
故答案为:k>﹣5.
21.解:∵A(﹣1,1),B(2,1),C(1,3).
∴当直线y=kx﹣2经过点A时,﹣k﹣2=1,解得k=﹣3;
当直线y=kx﹣2经过点B时,2k﹣2=1,解得k=,
∴k≤﹣3或0<k≤.
故答案为k≤﹣3或0<k≤.
22.解:∵直线y=﹣x+1与x轴、y轴分别交于点A、B,
∴A(2,0),B(0,1),
∵点P与点O关于直线AB对称,
∴直线OP为y=2x,OA=PA,
设P(m,2m),则(m﹣2)2+(2m)2=22,
解得m1=,m2=0(舍去),
∴P的坐标为(,),
故答案为(,).
23.解:作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图.
令y=x+3中x=0,则y=3,
∴点B的坐标为(0,3);
令y=x+3中y=0,则x+3=0,解得:x=﹣8,
∴点A的坐标为(86,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(﹣4,),点D(0,).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,﹣),
∴PC+PD的最小值=CD′==5,
故答案为:5.
24.解:设直线OA的解析式为:y=kx,
把(1,2)代入,得k=2,
则直线OA解析式是:y=2x.
将其上平移2个单位长度,则平移后的直线的表达式为:y=2x+2.
故答案是:y=2x+2.
25.解:设直线y=3x﹣2向上平移h个单位,其图象经过点(2,10),
则函数解析式为y=3x﹣2+h,将点(2,10)代入,
得10=3×2﹣2+h,
解得h=6.
故答案为:6.
三.解答题
26.解:(1)如图所示;
(2)如图所示.
27.解:(1)列表:
描点,连线,
;
(2)由图象可得,
y>0时自变量x的取值范围是x>1.
28.解:(1)由题意得:2m+1<0,
解得:m<﹣.
(2)将点(﹣1,1)代入可得:1=﹣(2m+1)+3+m,
解得:m=1,
∴y=3x+4,
令x=0,则y=4,
∴图象经过点(﹣1,1),(0,4),
如图:
29.解(1)∵A(1,1),B(5,4),
∴d(A,B)=|xA﹣xB|+|yA﹣yB|=|1﹣5|+|1﹣4|=7;
(2)由题意得d(O,P)=|0﹣x|+|0﹣y|=2,
∴|x|+|y|=2,
所有符合条件的点P组成的图形如图所示:
(3)∵Q点在直线y=x+2,
∴Q(x,x+2),
∴d(Q,M)=|xQ﹣xM|+|yQ﹣yM|=|x﹣1|+|x+2﹣(﹣3)|=|x﹣1|+|x+5|,
又∵x可取一切实数,|x﹣1|+|x+5|表示数轴上实数x所对应的点到数1和﹣5所对应的点的距离之和,其最小值为6,
∴M(1,﹣3)到直线y=x+2的直角距离为6.
30.解:(1)设正比例函数的解析式为y=kx,
把A(2,3),代入得到k=,
∴正比例函数的解析式为y=x.
(2)将直线y=x向上平移3个单位,得直线y=x+3,如图;
4.4.一次函数的应用
一、选择题
甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离千米与甲出发的时间分之间的关系如图所示,乙从B地到A地需要分钟.
A. 12 B. 14 C. 18 D. 20
设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回,设x秒后两车间的距离为y米,y关于x的函数关系如图所示,则甲车的速度为
A. 10米秒 B. 11米秒 C. 12米秒 D. 13米秒
公式表示当重力为P时的物体作用在弹簧上时弹簧的长度,代表弹簧的初始长度,用厘米表示,K表示单位重力物体作用在弹簧上时弹簧拉伸的长度,用厘米表示.下面给出的四个公式中,表明这是一个短而硬的弹簧的是
A. B. C. D.
如图,表示一艘轮船和一艘快艇沿相同路线从甲港岀发到乙港行驶路程随时间变化的图象.则下列结论错误的是
A. 轮船的速度为20千米时
B. 快艇的速度为40千米时
C. 轮船比快艇先出发2小时
D. 快艇到达乙港用了6小时
某市体育馆将举办明星足球赛,为此体育馆推出两种团体购票方案设购票张数为x张,购票总价为y元方案一:购票总价由图中的折线OAB所表示的函数关系确定;方案二:提供8000元赞助后,每张票的票价为50元.则两种方案购票总价相同时,x的值为
A. 80 B. 120 C. 160 D. 200
如图,OA和BA分别表示甲乙两名学生运动的一次函数的图象,图中s和t分别表示路程和时间,根据图象判定跑260米时,快者比慢者少用多少秒
A. 6秒 B. 秒 C. 7秒 D. 秒
王亮家与姥姥家相距25km,王亮早上提前从家出发,骑自行车匀速去姥姥家,妈妈随后从家出发,乘车沿相同路线去姥姥家,王亮和妈妈的行进路程与王亮的行进时间之间的函数关系式的图象如图所示,则下列说法正确的是
A. 王亮骑自行车的速度是 B. 王亮比妈妈提前出发
C. 妈妈比王亮先到姥姥家 D. 妈妈从家到姥姥家共用了2h
一条公路旁依次有A,B,C三个村庄,甲乙两人骑自行车分别从A村、B村同时出发前往C村,甲乙之间的距离与骑行时间之间的函数关系如图所示,下列结论:
,B两村相距10km;
出发后两人相遇;
甲每小时比乙多骑行8km;
相遇后,乙又骑行了15min或65min时两人相距2km.
其中正确的个数是
A. 1个 B. 2个 C. 3个 D. 4个
端午节前夕举行了南通濠河国际龙舟邀请赛,在500米直道竞速赛道上,甲、乙两队所划行的路程单位:米与时间单位:分之间的函数关系式如图所示,根据图中提供的信息,
有下列说法:
甲队比乙队提前分到达终点
当划行1分钟时,甲队比乙队落后50米
当划行分钟时,甲队追上乙队
当甲队追上乙队时,两队划行的路程都是300米
其中错误的是
A. B. C. D.
甲、乙两车分别从A,B两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为,甲、乙两车离AB中点C的路程千米与甲车出发时间时的关系图象如图所示,则下列说法错误的是
A. A,B两地之间的距离为180千米
B. 乙车的速度为36千米时
C. a的值为
D. 当乙车到达终点时,甲车距离终点还有30千米
二、计算题
抗击新冠疫情期间,一方危急,八方支援.当吉林市疫情严重时,急需大量医疗防护物资.现知A城有医疗防护物资200t,B城有医疗防护物资现要把这些医疗物资全部运往C、D两市.从A城往C、D两市的运费分别为20元和25元;从B城往C、D两市的运费分别为15元和24元现C市需要物资240t,D市需要物资若设从A城往C市运请回答下列问题:
用含x的式子表示从A往D市运物资的数量为t,从B往C市运物资的数量为t,从B往D市运物资的数量为写化简后的式子.
求出怎样调运物资可使总运费最少?最少运费是多少?
赛龙舟是端午节的主要习俗,某市甲、乙两支龙舟队在端午节期间进行划龙舟比赛,从起点A驶向终点B,在整个行程中,龙舟离开起点的距离米与时间分钟的对应关系如图所示,请结合图象解答下列问题
起点A与终点B之间相距______米.
哪支龙舟队先到达终点?______填“甲”或“乙”
分别求甲、乙两支龙舟队离开起点的距离y关于x的函数关系式;
甲龙舟队出发多长时间时,两支龙舟队相距200米?
三、解答题
自2017年3月起,成都市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第I级:居民每户每月用水18吨以内含18吨每吨收水费a元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过部分每吨收水费b元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第I、Ⅱ级标准收费,超过部分每吨收水费c元.
设一户居民月用水x吨,应缴水费为y元,y与x之间的函数关系如图所示
根据图象直接作答:______,______;
求当时y与x之间的函数关系;
把上述水费阶梯收费办法称为方案,假设还存在方案:居民每户月用水一律按照每吨4元的标准缴费,请你根据居民每户月“用水量的大小设计出对居民缴费最实惠的方案.写出过程
星期五小颖放学步行从学校回家,当她走了一段路后,想起要去买彩笔做画报,于是原路返回到刚经过的文具用品店.买到彩笔后继续往家走如图是她离家的距离与所用时间的关系示意图,请根据图中提供的信息回答下列问题:
小颖家与学校的距离是______米;
表示的实际意义是______;
小颖本次从学校回家的整个过程中,走的路程是多少米?
买到彩笔后,小颖从文具用品店回到家步行的速度是多少米分?
答案
1.【答案】A2.【答案】B3.【答案】A4.【答案】D5.【答案】D
6.【答案】D7.【答案】A8.【答案】D9.【答案】D10.【答案】D
11.【答案】解:用含x的式子表示从A往D市运????,
从B往C市运??,
从B往?D市运???,
设总运费为W元,则有
???
,
,W随x的增大而增大,
当时,W有最小值,
即从A往D调200t,从B往D调60t,从B往C调240t时,总运费最少为10040元.
12.【答案】解:;
乙;
设甲龙舟队的y与x函数关系式为,
把代入,可得,
解得,
甲龙舟队的y与x函数关系式为,
设乙龙舟队的y与x函数关系式为,
把,代入,可得
,
解得,
乙龙舟队的y与x函数关系式为;
令,可得,
即当时,两龙舟队相遇,
当时,令,则符合题意;
当时,令,则符合题意;
当时,令,则符合题意;
当时,令,则符合题意;
综上所述,甲龙舟队出发或10或15或分钟时,两支龙舟队相距200米.
13.【答案】,4;
解:设当时,y与x之间的函数关系式为,
将,代入,得:,
解得:,
当时,y与x之间的函数关系式为.
?解:根据题意得:选择缴费方案需交水费元与用水数量吨之间的函数关系式为.
当时,;
当时,;
当时,.
当时,选择缴费方案更实惠;当时,选择两种缴费方案费用相同;当时,选择缴费方案更实惠.
14.【答案】解:小颖家与学校的距离是2600米;
故答案为:2600;
表示的实际意义是小颖在文具用品店买彩笔所花时间;
故答案为:小颖在文具用品店买彩笔所花时间;
米,
答:小颖本次从学校回家的整个过程中,走的路程是3400米;
米分,
买到彩笔后,小颖从文具用品店回到家步行的速度是90米分.
一.选择题
1.在①y=﹣8x;②y=﹣;③y=+1;④y=﹣8x2+6;⑤y=﹣0.5x﹣1中,一次函数有( )
A.1个 B.2个 C.3个 D.4个
2.下列关系式中,一次函数是( )
A.y=﹣1 B.y=x2+3
C.y=k+b(k、b是常数) D.y=3x
3.函数①y=πx;②y=2x﹣1;③y=,④y=x2﹣1中,y是x的一次函数的有( )
A.1个 B.2个 C.3个 D.4个
4.下列函数中:①y=﹣x;②y=;③y=;④y=2x+1,其中一次函数的个数是( )
A.1 B.2 C.3 D.4
5.下列函数中,y是x的一次函数的是( )
A.y=x2+2x B. C.y=x D.
6.若函数y=(m﹣1)x+3是一次函数,则m的值为( )
A.﹣1 B.1 C.0 D.﹣1或1
7.下列函数中,是一次函数的有( )
A. B.y=3x+1
C. D.y=ax﹣2(a为常数)
8.若函数y=(m﹣1)x|m|是正比例函数,则m的值为( )
A.1 B.﹣1 C.±1 D.2
9.下列函数中,正比例函数是( )
A.y=﹣3x+1 B.y=﹣ C.y=﹣x2+3 D.y=﹣
10.下列函数中,正比例函数是( )
A.y=﹣8x B.y= C.y=x2 D.y=8x﹣4
11.已知函数y=(2﹣m)x|m﹣1|是正比例函数,则m的值是( )
A.1 B.2或0 C.2 D.0
12.一次函数y=kx﹣b的图象如图所示,则关于x的方程kx﹣b=0的解是( )
A.(1,0) B.(0,﹣1) C.x=1 D.x=﹣1
13.一次函数y=kx+b的图象如图所示,则关于x的方程kx+b=﹣2的解为( )
A.x=0 B.x=﹣1 C.x=2 D.x=﹣2
14.已知一次函数y=kx+b的图象如图所示,则关于x的方程kx+b=0的解为( )
A.x=3 B.x=1.5 C.x=﹣3 D.x=﹣1.5
15.若一次函数y=x+n(n为常数)的图象如图所示,则关于x的一元一次方程x+n=0的解为( )
A.x=0 B. C.x=1 D.x=2
二.填空题
16.在一次函数y=﹣2(x+1)+x中,k为 ,b为 .
17.当m= 时,函数y=(m+1)x+5是一次函数.
18.已知y=(m﹣1)x﹣1是关于x的一次函数,则m为 .
19.已知一次函数y=(m﹣1)x|m|﹣2,则m= .
20.若y=(k﹣1)x2﹣|k|+k+1是关于x的正比例函数,则k= .
21.如果函数y=(m﹣)x是正比例函数,那么m= .
22.若y=(m﹣2)x+5是一次函数函数,则其解析式为 .
23.已知y﹣2与x+3成正比,且当x=1时,y=﹣6,则y与x的关系式是 .
24.若函数是正比例函数,则该函数表达式是 .
25.一次函数y=kx+b的图象如图所示,则关于x的方程kx+b=﹣1的解为 .
三.解答题
26.当k为何值时,函数y=(k+3)xk+1+4x﹣8(x≠0)是一次函数?
27.已知,直线L经过点A(4,0),B(0,2).
(1)画出直线L的图象,并求出直线L的解析式;
(2)求S△AOB;
(3)在x轴上是否存在一点P,使S△PAB=3?若存在,求出点P的坐标,若不存在,请说明理由.
28.如图,边长为4的等边△ABC,请建立适当的直角坐标系,使得点B的坐标为(4,0),并求出直线AC的关系式.
29.已知y﹣3与x+2成正比例,且当x=1时,y=6.求y与x之间的函数关系式.
30.已知函数y=(m﹣2)x+4+n.
(1)当m,n为何值时,y是x的一次函数,并写出关系式;
(2)当m,n为何值时,y是x的正比例函数,并写出关系式.
参考答案
一.选择题
1.解:①y=﹣8x属于一次函数;
②y=﹣属于反比例函数;
③y=+1不属于一次函数;
④y=﹣8x2+6属于二次函数;
⑤y=﹣0.5x﹣1属于一次函数,
∴一次函数有2个,
故选:B.
2.解:A、自变量在分母上,不符合一次函数定义,故此选项不符合题意;
B、y=x2+3是二次函数,不是一次函数,故此选项不符合题意;
C、少x,不符合一次函数定义,故此选项不符合题意;
D、y=3x是正比例函数也是一次函数,故此选项符合题意;
故选:D.
3.解:①y=πx;②y=2x﹣1是一次函数;
③y=是反比例函数,不是一次函数;
④y=x2﹣1是二次函数,不是一次函数,
因此一次函数共2个,
故选:B.
4.解:①y=﹣x;②y=;④y=2x+1是一次函数,共3个,
故选:C.
5.解:A.y=x2+2x属于二次函数,不合题意;
B.y=属于反比例函数,不合题意;
C.y=x属于一次函数,符合题意;
D.y=+1不是一次函数,不合题意;
故选:C.
6.解:由题意得:m2=1,且m﹣1≠0,
解得:m=﹣1,
故选:A.
7.解:A、y=x2不符合一次函数的定义,故此选项不合题意;
B、y=3x+1属于一次函数,故此选项符合题意;
C、y=不符合一次函数的定义,故此选项不合题意;
D、y=ax﹣2不符合一次函数的定义,故此选项不合题意;
故选:B.
8.解:由题意得:m﹣1≠0,|m|=1,
解得:m=﹣1.
故选:B.
9.解:A.是一次函数,不是正比例函数,故本选项不符合题意;
B.是正比例函数,故本选项符合题意;
C.是二次函数,不是正比例函数,故本选项不符合题意;
D.是反比例函数,不是正比例函数,故本选项不符合题意;
故选:B.
10.解:A、是正比例函数,故此选项符合题意;
B、是反比例函数,不是正比例函数,故此选项不合题意;
C、是二次函数,不是正比例函数,故此选项不合题意;
D、是一次函数,不是正比例函数,故此选项不合题意;
故选:A.
11.解:∵函数y=(2﹣m)x|m﹣1|是正比例函数,
∴|m﹣1|=1,且2﹣m≠0,
∴m﹣1=±1,且m≠2,
解得m=0.
故选:D.
12.解:从图象知,函数y=kx﹣b的图象经过点(1,0),
∴关于x的方程kx﹣b=0的解是x=1.
故选:C.
13.解:∵从图象可知:一次函数y=kx+b的图象与直线y=﹣2的交点坐标为(﹣1,﹣2),
∴关于x的方程kx+b=﹣2的解为x=﹣1,
故选:B.
14.解:由一次函数y=kx+b的图象可得y=0时,x=1.5,
因此关于x的方程kx+b=0的解为x=1.5,
故选:B.
15.解:由一次函数y=x+n的图象可得:当y=0时,x=2,
因此一元一次方程x+n=0的解为x=2,
故选:D.
二.填空题
16.解:∵y=﹣2(x+1)+x,
∴y=﹣x﹣2,
∴k=﹣1,b=﹣2.
故答案为:﹣1;﹣2.
17.解:根据一次函数的定义,可知:m2=1,m+1≠0,
解得:m=±1且m≠﹣1,
∴m=1.
故答案为:1.
18.解:由题意得:m2=1,且m﹣1≠0,
解得:m=﹣1,
故答案为:﹣1.
19.解:∵y=(m﹣1)x|m|﹣2是一次函数,
∴|m|=1,m﹣1≠0,
解得m=﹣1.
故答案为:﹣1.
20.解:∵y=(k﹣1)x2﹣|k|+k+1,y是x的正比例函数,
∴2﹣|k|=1,且k﹣1≠0,k+1=0,
解得:k=﹣1.
故答案为:﹣1.
21.解:∵函数y=(m﹣)x是正比例函数,
∴m﹣0且m2﹣1=1,
解得:m=﹣,
故答案为:﹣.
22.解:∵y=(m﹣2)x+5是一次函数函数,
∴m﹣2≠0,且m2﹣3=1,
解得:m=﹣2,
∴y=﹣4x+5,
故答案为y=﹣4x+5.
23.解:设y﹣2=k(x+3),
根据题意得:﹣6﹣2=4k,
则k=﹣2,
则函数的解析式是:y=﹣2x﹣6.
故答案为y=﹣2x﹣6.
24.解:∵是正比例函数,
∴,
解得:m=﹣2,
该函数表达式是y=﹣4x,
故答案为:y=﹣4x.
25.解:∵一次函数y=kx+b的图象过点(,﹣1),
∴关于x的方程kx+b=﹣1的解是x=,
故答案为:x=.
三.解答题
26.解:∵y=(k+3)xk+1+4x﹣8(x≠0),
∴k+1=1,k+3+4≠0,
解得:k=0.
∴当k为0时,函数y=(k+3)xk+1+4x﹣8(x≠0)是一次函数.
27.解:(1)画出函数图象如图:
设直线l的解析式为y=kx+b,
把A(4,0)、点B(0,2)分别代入得,解得,
∴一次函数解析式为y=﹣x+2;
(2)∵点A(4,0),B(0,2).
∴OA=4,OB=2,
∴S△AOB==4;
(3)在x轴上存在一点P,使S△PAB=3,理由如下:
设P(x,0),
∵A(4,0)、B(0,2),
∴PA=|x﹣4|,
∵S△PAB=3,
∴PA?OB=3,即|x﹣4|×2=3,
∴x﹣4=±3,
∴x=7或1,
∴P的坐标为(7,0)或(1,0).
28.解:以A为原点,AB所在直线为x轴建立直角坐标系,
此时A、B点的坐标分别为(0,0)、(4,0),
作CD⊥AB于D,则AD=BD=AB=2.
∴CD===2,
∴C(2,2),
设直线AC的解析式为y=kx,
把C(2,2)代入得,2=2k,
解得k=,
∴直线AC的关系式为y=x.
29.解:设y﹣3=k(x+2)(k≠0).
∵当x=1时,y=6,
∴k(1+2)=6﹣3,
解得 k=1,
所以y与x之间的函数关系式为:y=x+5.
30.解:(1)根据题意得,,
解得m=﹣2,
故当m=﹣2,n为任意实数时,y是x的一次函数,解析式为y=﹣4x+4+n,
(2)根据题意得,
解得m=﹣2,n=﹣4,
故m=﹣2,n=﹣4时,y是x的正比例函数,解析式为y=﹣4x.
4.3 一次函数的图象
一.选择题
1.在同一直角坐标系中,一次函数y=kx+b和y=bx+k的图象可能正确的是( )
A. B.
C. D.
2.下面所画的函数图象中,不可能是一次函数y=mx+2﹣m图象的是( )
A. B.
C. D.
3.一次函数y1=kx+b与y2=bx+k(k,b为常数)在同一平面直角坐标系中大致图象可能是( )
A. B.
C. D.
4.下列图形中,表示一次函数y=mx+n与正比例函数y=﹣mnx(m,n为常数,且mn≠0)的图象不正确的是( )
A. B.
C. D.
5.若正比例函数y=kx的图象如图所示,则一次函数y=﹣kx+k的图象大致是( )
A. B.
C. D.
6.点P1(x1,y1),点P2(x2,y2)是一次函数y=4x+3图象上的两个点,且x1<x2,则y1与y2的大小关系是( )
A.y1>y2 B.y1>y2>0 C.y1<y2 D.y1=y2
7.一次函数y=mx﹣n与y=mnx(mn≠0),在同一平面直角坐标系的图象不可能是( )
A. B.
C. D.
8.若a,b为实数,且++b=3,则直线y=ax﹣b不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.已知关于x的多项式x2+kx+1是一个完全平方式,则一次函数y=(k﹣2)x+5经过的象限是( )
A.第一、二、三象限 B.第二、三、四象限
C.第一、二、四象限 D.第一、三、四象限
10.如图,平面直角坐标系xOy中,阴影部分(射线y=x,x>0与y正半轴之间,不含边界)的点的坐标(x,y)满足( )
A.x=y B.x>y>0 C.y>x>0 D.y=x>0
11.下列一次函数中,y随x值的增大而减小的( )
A.y=2x+1 B.y=3﹣4x C.y=πx+2 D.y=(5﹣2)x
12.在一次函数y=(k﹣1)x的图象上,y都随x的增大而增大,则k的值可以是( )
A.﹣1 B.0 C.1 D.2
13.一次函数y=(m﹣1)x+3,y随x的增大而增大,则m的值可以为( )
A.0 B.1 C.2 D.﹣2
14.若点P在一次函数y=x﹣4的图象上,则点P一定不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
15.对于函数y=﹣3x+1,下列结论正确的是( )
A.它的图象必经过点(1,3)
B.y的值随x值的增大而增大
C.当x>0时,y<0
D.它的图象不经过第三象限
二.填空题
16.若点P(﹣1,y1)和点Q(﹣2,y2)是一次函数y=﹣x+b的图象上的两点,则y1,y2的大小关系是:y1 y2(填“>,<或=”).
17.直线ax+y﹣2a+1=0与直线(a+2)x﹣ay+3=0垂直,则a的值为 .
18.复习课中,教师给出关于x的函数y=﹣2mx+m﹣1(m≠0),学生们在独立思考后,给出了5条关于这个函数的结论:
①此函数是一次函数,但不可能是正比例函数;
②函数的值y随着自变量x的增大而减小;
③该函数图象与y轴的交点在y轴的正半轴上;
④若函数图象与x轴交于A(a,0),则a<0.5;
⑤此函数图象与直线y=4x﹣3,y轴成的面积必小于0.5.
对于以上5个结论正确有 个.
19.正比例函数y=﹣的图象经过第 象限.
20.已知正比例函数y=(1+)x,y随着x的增大而增大,则k的取值范围是 .
21.有一种动画设计,屏幕上的△ABC是黑色区域(含三角形的边界).其中A(﹣1,1),B(2,1),C(1,3).用信号枪沿直线y=kx﹣2发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的k的取值范围是 .
22.如图,平面直角坐标系中,直线y=﹣x+1与x轴、y轴分别交于点A、B,点P与点O关于直线AB对称,则点P的坐标为 .
23.如图,直线y=x+3与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为 .
24.如图,将直线OA向上平移2个单位长度,则平移后的直线的表达式为 .
25.要把直线y=3x﹣2向上平移,使其图象经过点(2,10),需要向上平移 个单位.
三.解答题
26.画出下列正比例函数和一次函数的图象:
(1)y=2x;
(2)y=﹣2x﹣4.
27.(1)在平面直角坐标系中,作出y=2x﹣2的图象.
(2)根据图象,直接写出y>0时自变量x的取值范围.
28.已知一次函数y=(2m+1)x+3+m.
(1)若y随x的增大而减小,求m的取值范围;
(2)若图象经过点(﹣1,1),求m的值,画出这个函数图象.
29.对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1﹣x2|+|y1﹣y2|叫做P1,P2两点间的直角距离,记作d(P1,P2).
(1)已知A(1,1),B(5,4),求d(A,B).
(2)已知点O为坐标原点,动点P(x,y)满足d(O,P)=2,请写出y与x之间的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形.
(3)设点P0(x0,y0)是一定点,点Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做点P0到直线y=ax+b的直角距离.试求点M(1,﹣3)到直线y=x+2的直角距离.
30.已知正比例函数的图象经过点A(2,3);
(1)求出此正比例函数表达式;
(2)该直线向上平移3个单位,写出平移后所得直线的表达式,并画出它的图象.
参考答案
一.选择题
1.解:A、一条直线反映k>0,b>0,一条直线反映k>0,b<0,故本选项错误;
B、一条直线反映出k>0,b<0,一条直线反映k>0,b<0,一致,故本选项正确;
C、一条直线反映k<0,b>0,一条直线反映k>0,b<0,故本选项错误;
D、一条直线反映k>0,b<0,一条直线反映k<0,b<0,故本选项错误.
故选:B.
2.解:根据图象知:
A、m<0,2﹣m>0.解得m<0,所以有可能;
B、m>0,2﹣m>0.解得0<m<2,所以有可能;
C、m<0,2﹣m<0.两不等式无公共部分,所以不可能;
D、m>0,2﹣m<0.解得m>2,所以有可能.
故选:C.
3.解:A、直线y1=kx+b反映k>0,b<0,直线y2=bx+k反映k>0,b>0,故本选项错误;
B、直线y1=kx+b反映k<0,b<0,直线y2=bx+k反映k>0,b<0,故本选项错误;
C、直线y1=kx+b反映k>0,b<0,直线y2=bx+k反映k<0,b<0,故本选项错误;
D、直线y1=kx+b反映k<0,b>0,直线y2=bx+k反映k<0,b>0,一致,故本选项正确.
故选:D.
4.解:①当﹣mn<0,m,n同号,同正时y=mx+n过一、二、三象限,同负时过二、三、四象限;
②当﹣mn>0时,m,n异号,则y=mx+n过一、三、四象限或一、二、四象限.
故选:B.
5.解:∵正比例函数y=kx的图象经过第二、四象限,
∴k<0,
∴﹣k>0,
∴y=﹣kx+k的图象经过一、三、四象限,
故选:D.
6.解:∵k=4>0,
∴y随x的增大而增大,
又∵x1<x2,
∴y1<y2.
故选:C.
7.解:当m>0,n>0时,一次函数y=mx﹣n的图象经过第一、三、四象限,一次函数y=mnx的图象经过第一、三象限,故选项B正确,选项C错误;
当m>0,n<0时,一次函数y=mx﹣n的图象经过第一、二、三象限,一次函数y=mnx的图象经过第二、四象限,故选项A正确;
当m<0,n<0时,一次函数y=mx﹣n的图象经过第一、二、四象限,一次函数y=mnx的图象经过第一、三象限,故选项D正确;
故选:C.
8.解:∵++b=3,
∴,
解得a=,
∴+b=3,
∴b=3,
∴直线y=x﹣3,该直线经过第一、三、四象限,不经过第二象限,
故选:B.
9.解:∵关于x的多项式x2+kx+1是一个完全平方式,
∴k=±2,
当k=2时,函数y=(2﹣2)x+5=5是常数函数,不是一次函数;
当k=﹣2时,一次函数y=(﹣2﹣2)x+5=﹣4x+5,则该函数经过第一、二、四象限,
故选:C.
10.解:当x=y>0时在射线y=x上,
故当y>x>0时点(x,y)在阴影部分内,
故选:C.
11.解:A、∵k=2>0,
∴y随x值的增大而增大;
B、∵k=﹣4<0,
∴y随x值的增大而减少;
C、∵k=π>0,
∴y随x值的增大而增大;
D、∵k=5﹣2=3>0,
∴y随x值的增大而增大.
故选:B.
12.解:∵一次函数y=(k﹣1)x的图象中,y随x的增大而增大,
∴k﹣1>0,解得k>1,
∴k可以取2.
故选:D.
13.解:∵一次函数y=(m﹣1)x+3,若y随x的增大而增大,
∴m﹣1>0,解得m>1,
只有2合适,
故选:C.
14.解:∵k=1>0,b=﹣4<0,
∴一次函数y=x﹣4的图象经过第一、三、四象限,
又∵点P在一次函数y=x﹣4的图象上,
∴点P一定不在第二象限.
故选:B.
15.解:A、当x=1时,y=﹣3×1+1=﹣2,
∴点(1,﹣2)在函数y=﹣3x+1的图象,结论A不正确;
B、∵k=﹣3<0,
∴y随x的增大而减小,结论B不正确;
C、当y=0时,﹣3x+1=0,解得:x=,
∴当0<x<时,y>0,结论C不正确;
D、∵k=﹣3<0,b=1>0,
∴函数y=﹣3x+1的图象经过第一、二、四象限,
∴函数y=﹣3x+1的图象不经过第三象限,结论D正确.
故选:D.
二.填空题
16.解:∵k=﹣1<0,
∴y随x的增大而减小,
又∵﹣1>﹣2,
∴y1<y2.
故答案为:<.
17.解:当a=0时,直线ax+y﹣2a+1=0可以写成直线y=﹣1,直线(a+2)x﹣ay+3=0可以写成x=﹣,此时直线ax+y﹣2a+1=0与直线(a+2)x﹣ay+3=0垂直;
当a≠0时,直线ax+y﹣2a+1=0可以写成直线y=﹣ax+2a﹣1,直线(a+2)x﹣ay+3=0可以写成直线y=x+,
∵直线ax+y﹣2a+1=0与直线(a+2)x﹣ay+3=0垂直,
∴﹣a=﹣1,
解得a=﹣1;
故答案为:0或﹣1.
18.解:此函数是一次函数,当m=1时,它是正比例函数,所以①错误;
当m<0时,函数的值y 随着自变量x的增大而增大,所以②错误;
当m<1时,该函数图象与y轴的交点在y轴的负半轴上,所以③错误;
若函数图象与x轴交于A(a,0),则﹣2ma+m﹣1=0,解得a==0.5﹣,当m>0时,a<0.5,当m<0时,a>0.5,所以④错误;
此函数图象与直线y=4x﹣3的交点坐标为(,﹣1),此直线与y轴的交点坐标为(0,m﹣1),直线y=4x﹣3与y轴的交点坐标为(0,﹣3),所以此函数图象与直线y=4x﹣3、y轴围成的面积=?|m﹣1+3|?=?|m+2|,当m=2时,面积为1,所以⑤错误.
故答案为:0.
19.解:由正比例函数y=﹣中的k=﹣,知函数y=﹣的图象经过第二、四象限.
故答案是:二、四.
20.解:∵正比例函数y=(1+)x中,y随x的增大而增大,
∴1+>0,
即k>﹣5.
故答案为:k>﹣5.
21.解:∵A(﹣1,1),B(2,1),C(1,3).
∴当直线y=kx﹣2经过点A时,﹣k﹣2=1,解得k=﹣3;
当直线y=kx﹣2经过点B时,2k﹣2=1,解得k=,
∴k≤﹣3或0<k≤.
故答案为k≤﹣3或0<k≤.
22.解:∵直线y=﹣x+1与x轴、y轴分别交于点A、B,
∴A(2,0),B(0,1),
∵点P与点O关于直线AB对称,
∴直线OP为y=2x,OA=PA,
设P(m,2m),则(m﹣2)2+(2m)2=22,
解得m1=,m2=0(舍去),
∴P的坐标为(,),
故答案为(,).
23.解:作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图.
令y=x+3中x=0,则y=3,
∴点B的坐标为(0,3);
令y=x+3中y=0,则x+3=0,解得:x=﹣8,
∴点A的坐标为(86,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(﹣4,),点D(0,).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,﹣),
∴PC+PD的最小值=CD′==5,
故答案为:5.
24.解:设直线OA的解析式为:y=kx,
把(1,2)代入,得k=2,
则直线OA解析式是:y=2x.
将其上平移2个单位长度,则平移后的直线的表达式为:y=2x+2.
故答案是:y=2x+2.
25.解:设直线y=3x﹣2向上平移h个单位,其图象经过点(2,10),
则函数解析式为y=3x﹣2+h,将点(2,10)代入,
得10=3×2﹣2+h,
解得h=6.
故答案为:6.
三.解答题
26.解:(1)如图所示;
(2)如图所示.
27.解:(1)列表:
描点,连线,
;
(2)由图象可得,
y>0时自变量x的取值范围是x>1.
28.解:(1)由题意得:2m+1<0,
解得:m<﹣.
(2)将点(﹣1,1)代入可得:1=﹣(2m+1)+3+m,
解得:m=1,
∴y=3x+4,
令x=0,则y=4,
∴图象经过点(﹣1,1),(0,4),
如图:
29.解(1)∵A(1,1),B(5,4),
∴d(A,B)=|xA﹣xB|+|yA﹣yB|=|1﹣5|+|1﹣4|=7;
(2)由题意得d(O,P)=|0﹣x|+|0﹣y|=2,
∴|x|+|y|=2,
所有符合条件的点P组成的图形如图所示:
(3)∵Q点在直线y=x+2,
∴Q(x,x+2),
∴d(Q,M)=|xQ﹣xM|+|yQ﹣yM|=|x﹣1|+|x+2﹣(﹣3)|=|x﹣1|+|x+5|,
又∵x可取一切实数,|x﹣1|+|x+5|表示数轴上实数x所对应的点到数1和﹣5所对应的点的距离之和,其最小值为6,
∴M(1,﹣3)到直线y=x+2的直角距离为6.
30.解:(1)设正比例函数的解析式为y=kx,
把A(2,3),代入得到k=,
∴正比例函数的解析式为y=x.
(2)将直线y=x向上平移3个单位,得直线y=x+3,如图;
4.4.一次函数的应用
一、选择题
甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离千米与甲出发的时间分之间的关系如图所示,乙从B地到A地需要分钟.
A. 12 B. 14 C. 18 D. 20
设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回,设x秒后两车间的距离为y米,y关于x的函数关系如图所示,则甲车的速度为
A. 10米秒 B. 11米秒 C. 12米秒 D. 13米秒
公式表示当重力为P时的物体作用在弹簧上时弹簧的长度,代表弹簧的初始长度,用厘米表示,K表示单位重力物体作用在弹簧上时弹簧拉伸的长度,用厘米表示.下面给出的四个公式中,表明这是一个短而硬的弹簧的是
A. B. C. D.
如图,表示一艘轮船和一艘快艇沿相同路线从甲港岀发到乙港行驶路程随时间变化的图象.则下列结论错误的是
A. 轮船的速度为20千米时
B. 快艇的速度为40千米时
C. 轮船比快艇先出发2小时
D. 快艇到达乙港用了6小时
某市体育馆将举办明星足球赛,为此体育馆推出两种团体购票方案设购票张数为x张,购票总价为y元方案一:购票总价由图中的折线OAB所表示的函数关系确定;方案二:提供8000元赞助后,每张票的票价为50元.则两种方案购票总价相同时,x的值为
A. 80 B. 120 C. 160 D. 200
如图,OA和BA分别表示甲乙两名学生运动的一次函数的图象,图中s和t分别表示路程和时间,根据图象判定跑260米时,快者比慢者少用多少秒
A. 6秒 B. 秒 C. 7秒 D. 秒
王亮家与姥姥家相距25km,王亮早上提前从家出发,骑自行车匀速去姥姥家,妈妈随后从家出发,乘车沿相同路线去姥姥家,王亮和妈妈的行进路程与王亮的行进时间之间的函数关系式的图象如图所示,则下列说法正确的是
A. 王亮骑自行车的速度是 B. 王亮比妈妈提前出发
C. 妈妈比王亮先到姥姥家 D. 妈妈从家到姥姥家共用了2h
一条公路旁依次有A,B,C三个村庄,甲乙两人骑自行车分别从A村、B村同时出发前往C村,甲乙之间的距离与骑行时间之间的函数关系如图所示,下列结论:
,B两村相距10km;
出发后两人相遇;
甲每小时比乙多骑行8km;
相遇后,乙又骑行了15min或65min时两人相距2km.
其中正确的个数是
A. 1个 B. 2个 C. 3个 D. 4个
端午节前夕举行了南通濠河国际龙舟邀请赛,在500米直道竞速赛道上,甲、乙两队所划行的路程单位:米与时间单位:分之间的函数关系式如图所示,根据图中提供的信息,
有下列说法:
甲队比乙队提前分到达终点
当划行1分钟时,甲队比乙队落后50米
当划行分钟时,甲队追上乙队
当甲队追上乙队时,两队划行的路程都是300米
其中错误的是
A. B. C. D.
甲、乙两车分别从A,B两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为,甲、乙两车离AB中点C的路程千米与甲车出发时间时的关系图象如图所示,则下列说法错误的是
A. A,B两地之间的距离为180千米
B. 乙车的速度为36千米时
C. a的值为
D. 当乙车到达终点时,甲车距离终点还有30千米
二、计算题
抗击新冠疫情期间,一方危急,八方支援.当吉林市疫情严重时,急需大量医疗防护物资.现知A城有医疗防护物资200t,B城有医疗防护物资现要把这些医疗物资全部运往C、D两市.从A城往C、D两市的运费分别为20元和25元;从B城往C、D两市的运费分别为15元和24元现C市需要物资240t,D市需要物资若设从A城往C市运请回答下列问题:
用含x的式子表示从A往D市运物资的数量为t,从B往C市运物资的数量为t,从B往D市运物资的数量为写化简后的式子.
求出怎样调运物资可使总运费最少?最少运费是多少?
赛龙舟是端午节的主要习俗,某市甲、乙两支龙舟队在端午节期间进行划龙舟比赛,从起点A驶向终点B,在整个行程中,龙舟离开起点的距离米与时间分钟的对应关系如图所示,请结合图象解答下列问题
起点A与终点B之间相距______米.
哪支龙舟队先到达终点?______填“甲”或“乙”
分别求甲、乙两支龙舟队离开起点的距离y关于x的函数关系式;
甲龙舟队出发多长时间时,两支龙舟队相距200米?
三、解答题
自2017年3月起,成都市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第I级:居民每户每月用水18吨以内含18吨每吨收水费a元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过部分每吨收水费b元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第I、Ⅱ级标准收费,超过部分每吨收水费c元.
设一户居民月用水x吨,应缴水费为y元,y与x之间的函数关系如图所示
根据图象直接作答:______,______;
求当时y与x之间的函数关系;
把上述水费阶梯收费办法称为方案,假设还存在方案:居民每户月用水一律按照每吨4元的标准缴费,请你根据居民每户月“用水量的大小设计出对居民缴费最实惠的方案.写出过程
星期五小颖放学步行从学校回家,当她走了一段路后,想起要去买彩笔做画报,于是原路返回到刚经过的文具用品店.买到彩笔后继续往家走如图是她离家的距离与所用时间的关系示意图,请根据图中提供的信息回答下列问题:
小颖家与学校的距离是______米;
表示的实际意义是______;
小颖本次从学校回家的整个过程中,走的路程是多少米?
买到彩笔后,小颖从文具用品店回到家步行的速度是多少米分?
答案
1.【答案】A2.【答案】B3.【答案】A4.【答案】D5.【答案】D
6.【答案】D7.【答案】A8.【答案】D9.【答案】D10.【答案】D
11.【答案】解:用含x的式子表示从A往D市运????,
从B往C市运??,
从B往?D市运???,
设总运费为W元,则有
???
,
,W随x的增大而增大,
当时,W有最小值,
即从A往D调200t,从B往D调60t,从B往C调240t时,总运费最少为10040元.
12.【答案】解:;
乙;
设甲龙舟队的y与x函数关系式为,
把代入,可得,
解得,
甲龙舟队的y与x函数关系式为,
设乙龙舟队的y与x函数关系式为,
把,代入,可得
,
解得,
乙龙舟队的y与x函数关系式为;
令,可得,
即当时,两龙舟队相遇,
当时,令,则符合题意;
当时,令,则符合题意;
当时,令,则符合题意;
当时,令,则符合题意;
综上所述,甲龙舟队出发或10或15或分钟时,两支龙舟队相距200米.
13.【答案】,4;
解:设当时,y与x之间的函数关系式为,
将,代入,得:,
解得:,
当时,y与x之间的函数关系式为.
?解:根据题意得:选择缴费方案需交水费元与用水数量吨之间的函数关系式为.
当时,;
当时,;
当时,.
当时,选择缴费方案更实惠;当时,选择两种缴费方案费用相同;当时,选择缴费方案更实惠.
14.【答案】解:小颖家与学校的距离是2600米;
故答案为:2600;
表示的实际意义是小颖在文具用品店买彩笔所花时间;
故答案为:小颖在文具用品店买彩笔所花时间;
米,
答:小颖本次从学校回家的整个过程中,走的路程是3400米;
米分,
买到彩笔后,小颖从文具用品店回到家步行的速度是90米分.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
