_鲁教版(五四制)八年级数学下册第八章《一元二次方程》达标检测卷(word版含答案)
文档属性
| 名称 | _鲁教版(五四制)八年级数学下册第八章《一元二次方程》达标检测卷(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 79.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 15:34:22 | ||
图片预览




文档简介
第八章达标检测卷
一、选择题(每题3分,共30分)
1.方程①2x2-9=0;②-=0;③xy+x2=9;④7x+6=x2中,一元二次方程有( )
A.1个
B.2个
C.3个
D.4个
2.下列一元二次方程中,没有实数根的是( )
A.x2-2x-3=0
B.x2-x+1=0
C.x2+2x+1=0
D.x2=1
3.已知关于x的一元二次方程x2+mx-8=0的一个实数根为2,则另一个实数根及m的值分别为( )
A.4,-2
B.-4,-2
C.4,2
D.-4,2
4.一元二次方程x2-8x-1=0配方后为( )
A.(x-4)2=17
B.(x+4)2=15
C.(x+4)2=17
D.(x-4)2=17或(x+4)2=17
5.已知x为实数,且满足(x2+3x)2+2(x2+3x)-3=0,那么x2+3x的值为( )
A.1
B.-3或1
C.3
D.-1或3
6.某单位要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排10场比赛,则参加比赛的球队应有( )
A.7队
B.6队
C.5队
D.4队
7.关于x的方程x2-ax+2a=0的两根的平方和是5,则a的值是( )
A.-1或5
B.1
C.5
D.-1
8.一个三角形的两边长分别为3和6,第三边的长是方程(x-2)(x-4)=0的根,则这个三角形的周长是( )
A.11
B.11或13
C.13
D.以上选项都不正确
9.若一元二次方程x2-2x-m=0无实数根,则一次函数y=(m+1)x+m-1的图象不经过第( )象限.
A.四
B.三
C.二
D.一
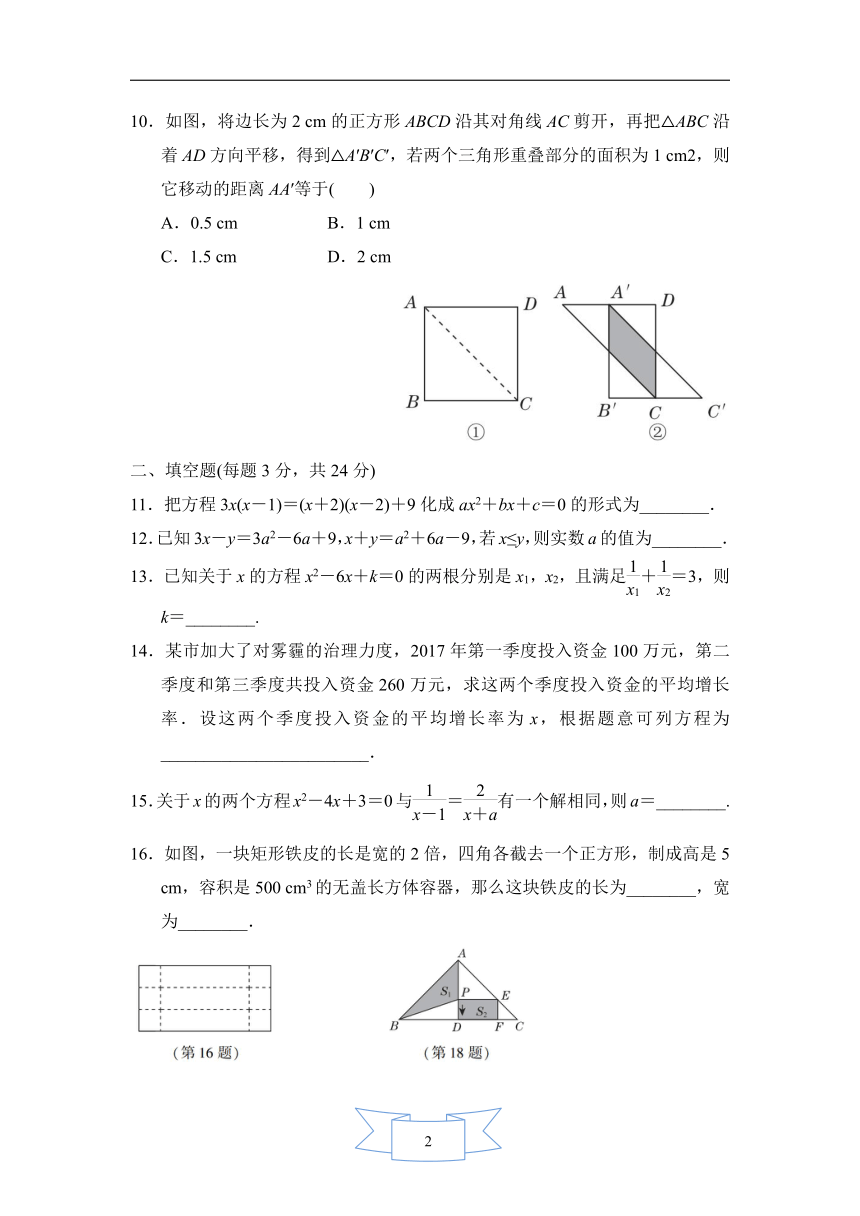
10.如图,将边长为2
cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1
cm2,则它移动的距离AA′等于( )
A.0.5
cm
B.1
cm
C.1.5
cm
D.2
cm
二、填空题(每题3分,共24分)
11.把方程3x(x-1)=(x+2)(x-2)+9化成ax2+bx+c=0的形式为________.
12.已知3x-y=3a2-6a+9,x+y=a2+6a-9,若x≤y,则实数a的值为________.
13.已知关于x的方程x2-6x+k=0的两根分别是x1,x2,且满足+=3,则k=________.
14.某市加大了对雾霾的治理力度,2017年第一季度投入资金100万元,第二季度和第三季度共投入资金260万元,求这两个季度投入资金的平均增长率.设这两个季度投入资金的平均增长率为x,根据题意可列方程为________________________.
15.关于x的两个方程x2-4x+3=0与=有一个解相同,则a=________.
16.如图,一块矩形铁皮的长是宽的2倍,四角各截去一个正方形,制成高是5
cm,容积是500
cm3的无盖长方体容器,那么这块铁皮的长为________,宽为________.
17.对于实数a,b,定义运算“
”:a
b=例如:4
2,因为4>2,所以4
2=42-4×2=8.若x1,x2是一元二次方程x2-5x+6=0的两个根,则x1
x2=________.
18.如图,在Rt△ABC中,∠BAC=90°,AB=AC=16
cm,AD为BC边上的高,动点P从点A出发,沿A→D方向以
cm/s的速度向点D运动.设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t
s(0三、解答题(19题12分,20~23题每题8分,24题10分,25题12分,共66分)
19.用适当的方法解下列方程.
(1)x2-x-1=0;
(2)x2-1=2(x+1);
(3)2x2-4
x=-3;
(4)(x+8)(x+1)=-12.
20.已知关于x的方程4x2-(k+2)x+k-1=0有两个相等的实数根.
(1)求k的值;
(2)求此时方程的根.
21.解方程(x-1)2-5(x-1)+4=0时,我们可以将x-1看成一个整体,设x-1=y,则原方程可化为y2-5y+4=0,解得y1=1,y2=4.当y=1时,即x-1=1,解得x=2;当y=4时,即x-1=4,解得x=5,所以原方程的解为x1=2,x2=5.请利用这种方法求方程(2x+5)2-4(2x+5)+3=0的解.
22.关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1,x2.
(1)求m的取值范围;
(2)若2(x1+x2)+x1x2+10=0,求m的值.
23.某商店以每件16元的价格购进一批商品,物价局限定每件商品的利润不得超过30%.
(1)根据物价局规定,此商品每件售价最高可定为多少元?
(2)若每件商品售价定为x元,则每天可卖出(170-5x)件,商店预期每天要盈利280元,那么每件商品的售价应定为多少元?
24.如图,在△ABC中,∠B=90°,AB=6
cm,BC=8
cm,若点P从点A沿AB边向点B以1
cm/s的速度移动,点Q从点B沿BC边向点C以2
cm/s的速度移动,两点同时出发.
(1)问几秒后,△PBQ的面积为8
cm2?
(2)出发几秒后,线段PQ的长为4
cm?
(3)△PBQ的面积能否为10
cm2?若能,求出时间;若不能,请说明理由.
25.杭州湾跨海大桥通车后,A地到宁波港的路程比原来缩短了120
km.已知运输车速度不变时,行驶时间将从原来的
h缩短到2
h.
(1)求A地经杭州湾跨海大桥到宁波港的路程.
(2)若货物运输费用包括运输成本和时间成本,某车货物从A地到宁波港的运输成本是每千米1.8元,时间成本是每时28元,那么该车货物从A地经杭州湾跨海大桥到宁波港的运输费用是多少元?
(3)A地准备开辟宁波方向的外运路线,即货物从A地经杭州湾跨海大桥到宁波港,再从宁波港运到B地.若有一批货物(不超过10车)从A地按外运路线运到B地的运费需8
320元,其中从A地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到B地的海上运费对一批不超过10车的货物计费方式是:1车800元,当货物每增加1车时,每车的海上运费就减少20元,问这批货物有几车?
答案
一、1.B 点拨:
因为②-=0中分母含有未知数;③xy+x2=9含有两个未知数,所以②③不是一元二次方程,而①④是一元二次方程.故选B.
2.B 3.D 4.A 5.A 6.C 7.D
8.C 9.D
10.B 点拨:
设AC交A′B′于H.
∵∠DAC=45°,∠AA′H=90°,
∴△AA′H是等腰直角三角形.
设AA′=x
cm,则A′H=x
cm,A′D=(2-x)cm.
∴x(2-x)=1,解得x1=x2=1,
即AA′=1
cm.故选B.
二、11.2x2-3x-5=0 12.3
13.2 点拨:
∵x2-6x+k=0的两根分别为x1,x2,
∴x1+x2=6,x1x2=k.
∴+===3.
解得k=2.经检验,k=2满足题意.
14.100(1+x)+100(1+x)2=260
点拨:
根据题意知:第二季度投入资金100(1+x)万元,第三季度投入资金100(1+x)2万元,
∴100(1+x)+100(1+x)2=260.
15.1 点拨:
由方程x2-4x+3=0,得
(x-1)(x-3)=0,
∴x-1=0或x-3=0.
解得x1=1,x2=3.
当x=1时,分式方程=无意义;
当x=3时,=,
解得a=1.
经检验,a=1是方程=的解.
16.30
cm;15
cm
17.3或-3 点拨:
x2-5x+6=0的两个根为x1=2,x2=3或x1=3,x2=2.
当x1=2,x2=3时,x1
x2=2×3-32=-3;
当x1=3,x2=2时,x1
x2=32-2×3=3.
18.6 点拨:
∵在Rt△ABC中,∠BAC=90°,AB=AC=16
cm,AD为BC边上的高,∴AD=BD=CD=8
cm.
又∵AP=t
cm,
∴S1=AP·BD=×t×8
=8t(cm2),PD=(8
-t)cm.易知PE=AP=t
cm,∴S2=PD·PE=(8
-t)·t
cm2.
∵S1=2S2,
∴8t=2(8
-t)·t.
解得t1=0(舍去),t2=6.
三、19.解:(1)(公式法)a=1,b=-1,c=-1,
所以b2-4ac=(-1)2-4×1×(-1)=5.
所以x==,
即原方程的根为x1=,
x2=.
(2)(因式分解法)移项,得x2-1-2(x+1)=0,
原方程可变形为(x+1)(x-1-2)=0,
解得x1=-1,x2=3.
(3)(公式法
)原方程可化为2x2-4
x+3=0,
∴a=2,b=-4
,c=3.
∴b2-4ac=(-4
)2-4×2×3=8.
∴x==,
即原方程的根为x1=,x2=.
(4)(因式分解法)原方程可化为x2+9x+20=0,
(x+4)(x+5)=0,
解得x1=-4,x2=-5.
20.解:(1)由题意得Δ=[-(k+2)]2-4×4×(k-1)=k2+4k+4-16k+16=k2-12k+20=0,解得k=2或k=10.
(2)当k=2时,原方程变为4x2-4x+1=0,(2x-1)2=0,即x1=x2=;当k=10时,原方程为4x2-12x+9=0,(2x-3)2=0,即x1=x2=.
21.解:设2x+5=y,则原方程可化为y2-4y+3=0,所以(y-1)(y-3)=0,解得y1=1,y2=3.当y=1时,即2x+5=1,解得x=-2;当y=3时,即2x+5=3,解得x=-1,所以原方程的解为x1=-2,x2=-1.
22.解:(1)由题意得Δ=9-4(m-1)≥0,∴m≤.
(2)由根与系数的关系得x1+x2=-3,x1x2=m-1.
∵2(x1+x2)+x1x2+10=0,
∴-6+(m-1)+10=0,∴m=-3,
∵m≤,∴m的值为-3.
23.解:(1)16(1+30%)=20.8(元),
即此商品每件售价最高可定为20.8元.
(2)(x-16)·(170-5x)=280,解得x1=20,x2=30.
因为售价最高不得高于20.8元,所以x2=30不合题意,应舍去.
故每件商品的售价应定为20元.
24.解:(1)设t
s后,△PBQ的面积为8
cm2,则PB=(6-t)cm,BQ=2t
cm,
∵∠B=90°,
∴(6-t)×2t=8,解得t1=2,t2=4,
∴2
s或4
s后,△PBQ的面积为8
cm2.
(2)设出发x
s后,PQ=4
cm,由题意,得(6-x)2+(2x)2=(4
)2,解得x1=,x2=2,故出发
s或2
s后,线段PQ的长为4
cm.
(3)不能.理由:设经过y
s,△PBQ的面积等于10
cm2,则×(6-y)×2y=10,即y2-6y+10=0,
∵Δ=b2-4ac=36-4×10=-4<0,
∴△PBQ的面积不能为10
cm2.
25.解:(1)设A地经杭州湾跨海大桥到宁波港的路程为x
km,
由题意得=,解得x=180.
∴A地经杭州湾跨海大桥到宁波港的路程为180
km.
(2)1.8×180+28×2=380(元),
∴该车货物从A地经杭州湾跨海大桥到宁波港的运输费用是380元.
(3)设这批货物有y车,由题意得y[800-20×(y-1)]+380y=8
320,整理得y2-60y+416=0,解得y1=8,y2=52(不合题意,舍去),
∴这批货物有8车.
一、选择题(每题3分,共30分)
1.方程①2x2-9=0;②-=0;③xy+x2=9;④7x+6=x2中,一元二次方程有( )
A.1个
B.2个
C.3个
D.4个
2.下列一元二次方程中,没有实数根的是( )
A.x2-2x-3=0
B.x2-x+1=0
C.x2+2x+1=0
D.x2=1
3.已知关于x的一元二次方程x2+mx-8=0的一个实数根为2,则另一个实数根及m的值分别为( )
A.4,-2
B.-4,-2
C.4,2
D.-4,2
4.一元二次方程x2-8x-1=0配方后为( )
A.(x-4)2=17
B.(x+4)2=15
C.(x+4)2=17
D.(x-4)2=17或(x+4)2=17
5.已知x为实数,且满足(x2+3x)2+2(x2+3x)-3=0,那么x2+3x的值为( )
A.1
B.-3或1
C.3
D.-1或3
6.某单位要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排10场比赛,则参加比赛的球队应有( )
A.7队
B.6队
C.5队
D.4队
7.关于x的方程x2-ax+2a=0的两根的平方和是5,则a的值是( )
A.-1或5
B.1
C.5
D.-1
8.一个三角形的两边长分别为3和6,第三边的长是方程(x-2)(x-4)=0的根,则这个三角形的周长是( )
A.11
B.11或13
C.13
D.以上选项都不正确
9.若一元二次方程x2-2x-m=0无实数根,则一次函数y=(m+1)x+m-1的图象不经过第( )象限.
A.四
B.三
C.二
D.一
10.如图,将边长为2
cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1
cm2,则它移动的距离AA′等于( )
A.0.5
cm
B.1
cm
C.1.5
cm
D.2
cm
二、填空题(每题3分,共24分)
11.把方程3x(x-1)=(x+2)(x-2)+9化成ax2+bx+c=0的形式为________.
12.已知3x-y=3a2-6a+9,x+y=a2+6a-9,若x≤y,则实数a的值为________.
13.已知关于x的方程x2-6x+k=0的两根分别是x1,x2,且满足+=3,则k=________.
14.某市加大了对雾霾的治理力度,2017年第一季度投入资金100万元,第二季度和第三季度共投入资金260万元,求这两个季度投入资金的平均增长率.设这两个季度投入资金的平均增长率为x,根据题意可列方程为________________________.
15.关于x的两个方程x2-4x+3=0与=有一个解相同,则a=________.
16.如图,一块矩形铁皮的长是宽的2倍,四角各截去一个正方形,制成高是5
cm,容积是500
cm3的无盖长方体容器,那么这块铁皮的长为________,宽为________.
17.对于实数a,b,定义运算“
”:a
b=例如:4
2,因为4>2,所以4
2=42-4×2=8.若x1,x2是一元二次方程x2-5x+6=0的两个根,则x1
x2=________.
18.如图,在Rt△ABC中,∠BAC=90°,AB=AC=16
cm,AD为BC边上的高,动点P从点A出发,沿A→D方向以
cm/s的速度向点D运动.设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t
s(0
19.用适当的方法解下列方程.
(1)x2-x-1=0;
(2)x2-1=2(x+1);
(3)2x2-4
x=-3;
(4)(x+8)(x+1)=-12.
20.已知关于x的方程4x2-(k+2)x+k-1=0有两个相等的实数根.
(1)求k的值;
(2)求此时方程的根.
21.解方程(x-1)2-5(x-1)+4=0时,我们可以将x-1看成一个整体,设x-1=y,则原方程可化为y2-5y+4=0,解得y1=1,y2=4.当y=1时,即x-1=1,解得x=2;当y=4时,即x-1=4,解得x=5,所以原方程的解为x1=2,x2=5.请利用这种方法求方程(2x+5)2-4(2x+5)+3=0的解.
22.关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1,x2.
(1)求m的取值范围;
(2)若2(x1+x2)+x1x2+10=0,求m的值.
23.某商店以每件16元的价格购进一批商品,物价局限定每件商品的利润不得超过30%.
(1)根据物价局规定,此商品每件售价最高可定为多少元?
(2)若每件商品售价定为x元,则每天可卖出(170-5x)件,商店预期每天要盈利280元,那么每件商品的售价应定为多少元?
24.如图,在△ABC中,∠B=90°,AB=6
cm,BC=8
cm,若点P从点A沿AB边向点B以1
cm/s的速度移动,点Q从点B沿BC边向点C以2
cm/s的速度移动,两点同时出发.
(1)问几秒后,△PBQ的面积为8
cm2?
(2)出发几秒后,线段PQ的长为4
cm?
(3)△PBQ的面积能否为10
cm2?若能,求出时间;若不能,请说明理由.
25.杭州湾跨海大桥通车后,A地到宁波港的路程比原来缩短了120
km.已知运输车速度不变时,行驶时间将从原来的
h缩短到2
h.
(1)求A地经杭州湾跨海大桥到宁波港的路程.
(2)若货物运输费用包括运输成本和时间成本,某车货物从A地到宁波港的运输成本是每千米1.8元,时间成本是每时28元,那么该车货物从A地经杭州湾跨海大桥到宁波港的运输费用是多少元?
(3)A地准备开辟宁波方向的外运路线,即货物从A地经杭州湾跨海大桥到宁波港,再从宁波港运到B地.若有一批货物(不超过10车)从A地按外运路线运到B地的运费需8
320元,其中从A地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到B地的海上运费对一批不超过10车的货物计费方式是:1车800元,当货物每增加1车时,每车的海上运费就减少20元,问这批货物有几车?
答案
一、1.B 点拨:
因为②-=0中分母含有未知数;③xy+x2=9含有两个未知数,所以②③不是一元二次方程,而①④是一元二次方程.故选B.
2.B 3.D 4.A 5.A 6.C 7.D
8.C 9.D
10.B 点拨:
设AC交A′B′于H.
∵∠DAC=45°,∠AA′H=90°,
∴△AA′H是等腰直角三角形.
设AA′=x
cm,则A′H=x
cm,A′D=(2-x)cm.
∴x(2-x)=1,解得x1=x2=1,
即AA′=1
cm.故选B.
二、11.2x2-3x-5=0 12.3
13.2 点拨:
∵x2-6x+k=0的两根分别为x1,x2,
∴x1+x2=6,x1x2=k.
∴+===3.
解得k=2.经检验,k=2满足题意.
14.100(1+x)+100(1+x)2=260
点拨:
根据题意知:第二季度投入资金100(1+x)万元,第三季度投入资金100(1+x)2万元,
∴100(1+x)+100(1+x)2=260.
15.1 点拨:
由方程x2-4x+3=0,得
(x-1)(x-3)=0,
∴x-1=0或x-3=0.
解得x1=1,x2=3.
当x=1时,分式方程=无意义;
当x=3时,=,
解得a=1.
经检验,a=1是方程=的解.
16.30
cm;15
cm
17.3或-3 点拨:
x2-5x+6=0的两个根为x1=2,x2=3或x1=3,x2=2.
当x1=2,x2=3时,x1
x2=2×3-32=-3;
当x1=3,x2=2时,x1
x2=32-2×3=3.
18.6 点拨:
∵在Rt△ABC中,∠BAC=90°,AB=AC=16
cm,AD为BC边上的高,∴AD=BD=CD=8
cm.
又∵AP=t
cm,
∴S1=AP·BD=×t×8
=8t(cm2),PD=(8
-t)cm.易知PE=AP=t
cm,∴S2=PD·PE=(8
-t)·t
cm2.
∵S1=2S2,
∴8t=2(8
-t)·t.
解得t1=0(舍去),t2=6.
三、19.解:(1)(公式法)a=1,b=-1,c=-1,
所以b2-4ac=(-1)2-4×1×(-1)=5.
所以x==,
即原方程的根为x1=,
x2=.
(2)(因式分解法)移项,得x2-1-2(x+1)=0,
原方程可变形为(x+1)(x-1-2)=0,
解得x1=-1,x2=3.
(3)(公式法
)原方程可化为2x2-4
x+3=0,
∴a=2,b=-4
,c=3.
∴b2-4ac=(-4
)2-4×2×3=8.
∴x==,
即原方程的根为x1=,x2=.
(4)(因式分解法)原方程可化为x2+9x+20=0,
(x+4)(x+5)=0,
解得x1=-4,x2=-5.
20.解:(1)由题意得Δ=[-(k+2)]2-4×4×(k-1)=k2+4k+4-16k+16=k2-12k+20=0,解得k=2或k=10.
(2)当k=2时,原方程变为4x2-4x+1=0,(2x-1)2=0,即x1=x2=;当k=10时,原方程为4x2-12x+9=0,(2x-3)2=0,即x1=x2=.
21.解:设2x+5=y,则原方程可化为y2-4y+3=0,所以(y-1)(y-3)=0,解得y1=1,y2=3.当y=1时,即2x+5=1,解得x=-2;当y=3时,即2x+5=3,解得x=-1,所以原方程的解为x1=-2,x2=-1.
22.解:(1)由题意得Δ=9-4(m-1)≥0,∴m≤.
(2)由根与系数的关系得x1+x2=-3,x1x2=m-1.
∵2(x1+x2)+x1x2+10=0,
∴-6+(m-1)+10=0,∴m=-3,
∵m≤,∴m的值为-3.
23.解:(1)16(1+30%)=20.8(元),
即此商品每件售价最高可定为20.8元.
(2)(x-16)·(170-5x)=280,解得x1=20,x2=30.
因为售价最高不得高于20.8元,所以x2=30不合题意,应舍去.
故每件商品的售价应定为20元.
24.解:(1)设t
s后,△PBQ的面积为8
cm2,则PB=(6-t)cm,BQ=2t
cm,
∵∠B=90°,
∴(6-t)×2t=8,解得t1=2,t2=4,
∴2
s或4
s后,△PBQ的面积为8
cm2.
(2)设出发x
s后,PQ=4
cm,由题意,得(6-x)2+(2x)2=(4
)2,解得x1=,x2=2,故出发
s或2
s后,线段PQ的长为4
cm.
(3)不能.理由:设经过y
s,△PBQ的面积等于10
cm2,则×(6-y)×2y=10,即y2-6y+10=0,
∵Δ=b2-4ac=36-4×10=-4<0,
∴△PBQ的面积不能为10
cm2.
25.解:(1)设A地经杭州湾跨海大桥到宁波港的路程为x
km,
由题意得=,解得x=180.
∴A地经杭州湾跨海大桥到宁波港的路程为180
km.
(2)1.8×180+28×2=380(元),
∴该车货物从A地经杭州湾跨海大桥到宁波港的运输费用是380元.
(3)设这批货物有y车,由题意得y[800-20×(y-1)]+380y=8
320,整理得y2-60y+416=0,解得y1=8,y2=52(不合题意,舍去),
∴这批货物有8车.
