_湘教版八年级数学下册第4章《一次函数》达标检测卷(word版含答案)
文档属性
| 名称 | _湘教版八年级数学下册第4章《一次函数》达标检测卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 315.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 15:36:42 | ||
图片预览




文档简介
第4章达标检测卷
一、选择题(每题3分,共30分)
1.下列图象中,不能表示y是x的函数的是( )
2.函数y=中自变量x的取值范围是( )
A.x>4
B.x≥4
C.x≤4
D.x≠4
3.一次函数y=-2x+1的图象不经过( )
A.第一象限
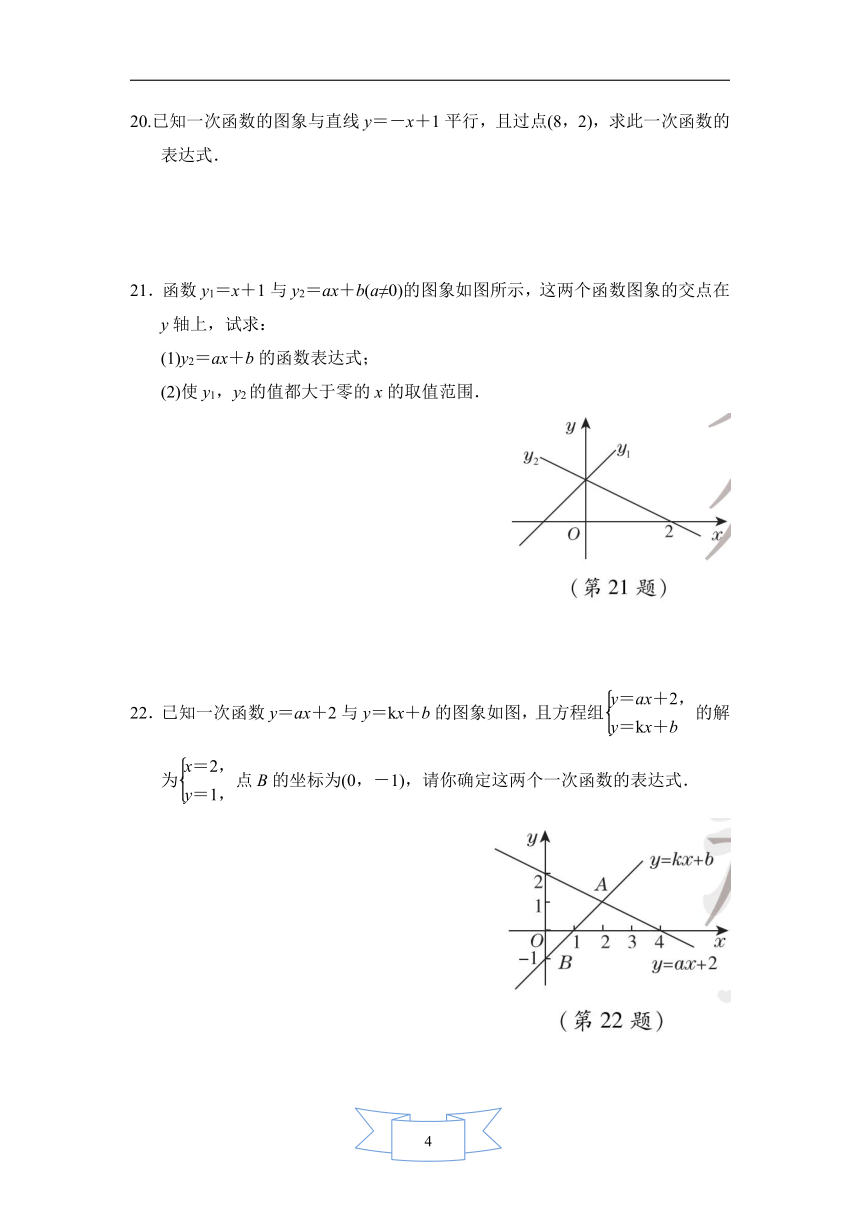
B.第二象限
C.第三象限
D.第四象限
4.已知在一次函数y=-1.5x+3的图象上,有三点(-3,y1),(-1,y2),(2,y3),则y1,y2,y3的大小关系为( )
A.y1>y2>y3
B.y1>y3>y2
C.y2>y1>y3
D.无法确定
5.如图,正方形ABCD的边长为4,点P为正方形ABCD边上一动点,沿A→D→C→B→A的路径匀速移动,回到点A后停止移动,设点P经过的路径长为x,△APD的面积为y,则下列图象中,能大致反映y与x之间的函数关系的是( )
6.已知一次函数y=kx+b,y随着x的增大而减小,且kb>0,则这个函数的大致图象是( )
7.直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图,则关于x的不等式k2x<k1x+b的解集为( )
A.x<-1
B.x>-1
C.x>1
D.x<1
8.把直线y=-x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,则m的取值范围是( )
A.1<m<7
B.3<m<4
C.m>1
D.m<4
9.已知一次函数y=x+m和y=-x+m的图象都经过点A(-2,0),且与y轴分别交于点B,C,那么△ABC的面积是( )
A.2
B.3
C.4
D.6
10.小文、小亮从学校出发到青少年宫参加书法比赛,小文步行一段时间后,小亮骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s(m)与小文出发时间t(min)之间的函数关系如图所示.下列说法:①小亮先到达青少年宫;②小亮的速度是小文速度的2.5倍;③a=24;④b=480.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题(每题3分,共24分)
11.圆的面积S与半径r之间的关系是S=πr2,其中自变量是__________,因变量是__________.
当r=20
cm时,S=__________cm2.
12.函数y=(m-2)x+m2-4是正比例函数,则m=________.
13.已知点P(a,-3)在一次函数y=2x+9的图象上,则a=________.
14.如果直线y=x+m与直线y=mx-1的交点坐标为(1,-2),那么m=________,m=________.
15.如图,一次函数y=kx+b的图象与x轴的交点坐标为(2,0),则下列说法:①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2.其中说法正确的有________(把你认为说法正确的序号都填上).
16.若一次函数y=(2m-1)x+3-2m的图象经过第一、二、四象限,则m的取值范围是__________.
17.一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,两车的距离y(千米)与慢车行驶的时间x(时)之间的函数关系如图所示,则快车到达乙地时慢车离乙地的距离为__________.
18.如图,在平面直角坐标系中,一次函数y=2x-1的图象分别交x轴、y轴于点A,B,将直线AB绕点B按顺时针方向旋转45°,交x轴于点C,则直线BC的函数表达式是
__________.
三、解答题(19,20题每题6分,21,22,23题每题10分,其余每题12分,共66分)
19.已知函数y=(m+2)x3-|m|+m-5.
(1)当m,m为何值时,此函数是一次函数?
(2)当m,m为何值时,此函数是正比例函数?
20.已知一次函数的图象与直线y=-x+1平行,且过点(8,2),求此一次函数的表达式.
21.函数y1=x+1与y2=ax+b(a≠0)的图象如图所示,这两个函数图象的交点在y轴上,试求:
(1)y2=ax+b的函数表达式;
(2)使y1,y2的值都大于零的x的取值范围.
22.已知一次函数y=ax+2与y=kx+b的图象如图,且方程组的解为点B的坐标为(0,-1),请你确定这两个一次函数的表达式.
23.植树节来临之际,学校准备购进一批树苗,已知2棵甲种树苗和5棵乙种树苗共需113元;3棵甲种树苗和2棵乙种树苗共需87元.
(1)求1棵甲种树苗和1棵乙种树苗的售价各是多少元?
(2)学校准备购进这两种树苗共100棵,并且乙种树苗的数量不多于甲种树苗数量的2倍,请设计出最省钱的购买方案,并求出此时的总费用.
24.如图,A,B分别是x轴上位于原点左、右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,S△AOP=6.
(1)求△COP的面积;
(2)求点A的坐标和p的值;
(3)若S△BOP=S△DOP,求直线BD的函数表达式.
25.甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地,40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地.甲、乙两车距A地的路程y(千米)与乙车行驶时间x(时)之间的函数图象如图所示.
请结合图象信息解答下列问题:
(1)直接写出a的值,并求甲车的速度;
(2)求图中线段EF所表示的y与x之间的函数表达式,并直接写出自变量x的取值范围;
(3)乙车出发多少小时与甲车相距15千米?
答案
一、1.B 2.B 3.C 4.A 5.B 6.B
7.B 8.C 9.C
10.B 点拨:由图象得出小文步行720
m,需要9
min,
∴小文的速度为720÷9=80(m/min),
当第15
min时,小亮骑了15-9=6(min),骑的路程为15×80=1
200(m),
∴小亮的速度为1
200÷6=200(m/min),
∴200÷80=2.5,故②正确;
当第19
min以后两人之间距离越来越近,说明小亮已经到达终点,则小亮先到达青少年宫,故①正确;
此时小亮骑了19-9=10(min),
骑的总路程为10×200=2
000(m),∴小文的步行时间为2
000÷80=25(min),
故a的值为25,故③错误;
∵小文19
min步行的路程为19×80=1
520(m),
∴b=2
000-1
520=480,故④正确.∴正确的有①②④.故选B.
二、11.r;S;400π 12.-2 13.-6
14.-1;- 15.①②③
16.m< 点拨:根据题意可知解不等式组即可.
17.450千米
18.y=x-1 点拨:根据已知条件得到A,B(0,-1),求得OA=,OB=1,过A作AF⊥AB交BC于F,过F作FE⊥x轴于E,则AB=AF,易得△ABO≌△FAE,
∴AE=OB=1,EF=OA=,
易得F,设直线BC的函数表达式为y=kx+b(k,b为常数,k≠0),将点B(0,-1),F的坐标分别代入,得解得
∴y=x-1.
三、19.解:(1)根据一次函数的定义,得3-|m|=1,且m+2≠0,解得m=2.
∴当m=2,n为任意实数时,此函数是一次函数.
(2)根据正比例函数的定义,得3-|m|=1,n-5=0,且m+2≠0,解得m=2,n=5.
∴当m=2,n=5时,此函数是正比例函数.
点拨:一次函数y=kx+b的表达式中,k≠0,自变量的次数为1,常数项b可以为任意实数;正比例函数y=kx的表达式中,比例系数k是常数,k≠0,自变量的次数为1.
20.解:设一次函数的表达式为y=kx+b,
∵一次函数的图象与直线y=-x+1平行,∴k=-1,
∴一次函数的表达式为y=-x+b.
∵一次函数的图象经过点(8,2),
∴2=-8+b,解得b=10,
∴一次函数的表达式为y=-x+10.
21.解:(1)对于函数y1=x+1,当x=0时,y1=1.
∴将点(0,1),点(2,0)的坐标分别代入y2=ax+b中,得
解得∴y2=-x+1.
(2)由y1>0,即x+1>0,得x>-1,
由y2>0,即-x+1>0,得x<2.
故使y1>0,y2>0的x的取值范围为-1<x<2.
22.解:因为方程组的解为
所以交点A的坐标为(2,1),所以将点A的坐标代入y=ax+2,得2a+2=1,解得a=-.
又因为函数y=kx+b的图象过点A(2,1)和点B(0,-1),
所以将点A,B的坐标分别代入y=kx+b,得解得
所以这两个一次函数的表达式分别为y=-x+2,y=x-1.
23.解:(1)设1棵甲种树苗的售价为x元,1棵乙种树苗的售价为y元,根据题意得解得
答:1棵甲种树苗的售价为19元,1棵乙种树苗的售价为15元.
(2)设购买甲种树苗a棵,则购买乙种树苗(100-a)棵,总费用为w元,依题意,得w=19a+15(100-a)=4a+1
500.
∵4>0,∴w随着a的增大而增大.
∴当a取最小值时,w有最小值.
∵100-a≤2a,∴a≥.
又∵a为整数.
∴当a=34时,w最小,且w最小=4×34+1
500=1
636,此时100-a=66.
∴最省钱的购买方案为购买甲种树苗34棵,购买乙种树苗66棵,总费用为1
636元.
24.解:(1)过点P作PF⊥y轴于点F.
∵点P的横坐标是2,∴PF=2.
又∵点C(0,2),∴OC=2,
∴S△COP=OC·PF=×2×2=2.
(2)∵S△AOC=S△AOP-S△COP=6-2=4,
∴S△AOC=OA·OC=4,即×OA×2=4,
∴OA=4,∴点A的坐标是(-4,0).
设直线AP的表达式是y=kx+b,将点A,C的坐标分别代入,得
解得
∴直线AP的表达式是y=x+2.
当x=2时,y=3,即p=3.
(3)设直线BD的表达式为y=ax+c,
∴点D的坐标为(0,c),点B的坐标为.
∵S△BOP=S△DOP,
∴OD·2=OB·3,
即c·2=·3.
由题意知c≠0,∴a=-,
∴直线BD的表达式是y=-x+c.
将点P(2,3)的坐标代入得3=-×2+c,解得c=6,∴直线BD的表达式是y=-x+6.
25.解:(1)a=4.5,甲车的速度为=60(千米/时).
(2)设乙车开始的速度为v千米/时,则4v+(7-4.5)×(v-50)=460,解得v=90,4v=360,
则D(4,360),E(4.5,360).
设直线EF对应的函数表达式为y=kx+b,把点E(4.5,360),点F(7,460)的坐标分别代入,得
解得
所以线段EF所表示的y与x之间的函数表达式为y=40x+180(4.5≤x≤7).
(3)60×=40(千米),则C(0,40),设直线CF对应的函数表达式为y=mx+n.
把点C(0,40),点F(7,460)的坐标分别代入,得解得
所以直线CF对应的函数表达式为y=60x+40,易得线段OD对应的函数表达式为y=90x(0≤x≤4),设CF交OD于点G,易得G,当0≤x≤时,60x+40-90x=15,解得x=;
当当4.5所以乙车出发小时或小时或小时与甲车相距15千米.
一、选择题(每题3分,共30分)
1.下列图象中,不能表示y是x的函数的是( )
2.函数y=中自变量x的取值范围是( )
A.x>4
B.x≥4
C.x≤4
D.x≠4
3.一次函数y=-2x+1的图象不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.已知在一次函数y=-1.5x+3的图象上,有三点(-3,y1),(-1,y2),(2,y3),则y1,y2,y3的大小关系为( )
A.y1>y2>y3
B.y1>y3>y2
C.y2>y1>y3
D.无法确定
5.如图,正方形ABCD的边长为4,点P为正方形ABCD边上一动点,沿A→D→C→B→A的路径匀速移动,回到点A后停止移动,设点P经过的路径长为x,△APD的面积为y,则下列图象中,能大致反映y与x之间的函数关系的是( )
6.已知一次函数y=kx+b,y随着x的增大而减小,且kb>0,则这个函数的大致图象是( )
7.直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图,则关于x的不等式k2x<k1x+b的解集为( )
A.x<-1
B.x>-1
C.x>1
D.x<1
8.把直线y=-x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,则m的取值范围是( )
A.1<m<7
B.3<m<4
C.m>1
D.m<4
9.已知一次函数y=x+m和y=-x+m的图象都经过点A(-2,0),且与y轴分别交于点B,C,那么△ABC的面积是( )
A.2
B.3
C.4
D.6
10.小文、小亮从学校出发到青少年宫参加书法比赛,小文步行一段时间后,小亮骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s(m)与小文出发时间t(min)之间的函数关系如图所示.下列说法:①小亮先到达青少年宫;②小亮的速度是小文速度的2.5倍;③a=24;④b=480.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题(每题3分,共24分)
11.圆的面积S与半径r之间的关系是S=πr2,其中自变量是__________,因变量是__________.
当r=20
cm时,S=__________cm2.
12.函数y=(m-2)x+m2-4是正比例函数,则m=________.
13.已知点P(a,-3)在一次函数y=2x+9的图象上,则a=________.
14.如果直线y=x+m与直线y=mx-1的交点坐标为(1,-2),那么m=________,m=________.
15.如图,一次函数y=kx+b的图象与x轴的交点坐标为(2,0),则下列说法:①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2.其中说法正确的有________(把你认为说法正确的序号都填上).
16.若一次函数y=(2m-1)x+3-2m的图象经过第一、二、四象限,则m的取值范围是__________.
17.一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,两车的距离y(千米)与慢车行驶的时间x(时)之间的函数关系如图所示,则快车到达乙地时慢车离乙地的距离为__________.
18.如图,在平面直角坐标系中,一次函数y=2x-1的图象分别交x轴、y轴于点A,B,将直线AB绕点B按顺时针方向旋转45°,交x轴于点C,则直线BC的函数表达式是
__________.
三、解答题(19,20题每题6分,21,22,23题每题10分,其余每题12分,共66分)
19.已知函数y=(m+2)x3-|m|+m-5.
(1)当m,m为何值时,此函数是一次函数?
(2)当m,m为何值时,此函数是正比例函数?
20.已知一次函数的图象与直线y=-x+1平行,且过点(8,2),求此一次函数的表达式.
21.函数y1=x+1与y2=ax+b(a≠0)的图象如图所示,这两个函数图象的交点在y轴上,试求:
(1)y2=ax+b的函数表达式;
(2)使y1,y2的值都大于零的x的取值范围.
22.已知一次函数y=ax+2与y=kx+b的图象如图,且方程组的解为点B的坐标为(0,-1),请你确定这两个一次函数的表达式.
23.植树节来临之际,学校准备购进一批树苗,已知2棵甲种树苗和5棵乙种树苗共需113元;3棵甲种树苗和2棵乙种树苗共需87元.
(1)求1棵甲种树苗和1棵乙种树苗的售价各是多少元?
(2)学校准备购进这两种树苗共100棵,并且乙种树苗的数量不多于甲种树苗数量的2倍,请设计出最省钱的购买方案,并求出此时的总费用.
24.如图,A,B分别是x轴上位于原点左、右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,S△AOP=6.
(1)求△COP的面积;
(2)求点A的坐标和p的值;
(3)若S△BOP=S△DOP,求直线BD的函数表达式.
25.甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地,40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地.甲、乙两车距A地的路程y(千米)与乙车行驶时间x(时)之间的函数图象如图所示.
请结合图象信息解答下列问题:
(1)直接写出a的值,并求甲车的速度;
(2)求图中线段EF所表示的y与x之间的函数表达式,并直接写出自变量x的取值范围;
(3)乙车出发多少小时与甲车相距15千米?
答案
一、1.B 2.B 3.C 4.A 5.B 6.B
7.B 8.C 9.C
10.B 点拨:由图象得出小文步行720
m,需要9
min,
∴小文的速度为720÷9=80(m/min),
当第15
min时,小亮骑了15-9=6(min),骑的路程为15×80=1
200(m),
∴小亮的速度为1
200÷6=200(m/min),
∴200÷80=2.5,故②正确;
当第19
min以后两人之间距离越来越近,说明小亮已经到达终点,则小亮先到达青少年宫,故①正确;
此时小亮骑了19-9=10(min),
骑的总路程为10×200=2
000(m),∴小文的步行时间为2
000÷80=25(min),
故a的值为25,故③错误;
∵小文19
min步行的路程为19×80=1
520(m),
∴b=2
000-1
520=480,故④正确.∴正确的有①②④.故选B.
二、11.r;S;400π 12.-2 13.-6
14.-1;- 15.①②③
16.m< 点拨:根据题意可知解不等式组即可.
17.450千米
18.y=x-1 点拨:根据已知条件得到A,B(0,-1),求得OA=,OB=1,过A作AF⊥AB交BC于F,过F作FE⊥x轴于E,则AB=AF,易得△ABO≌△FAE,
∴AE=OB=1,EF=OA=,
易得F,设直线BC的函数表达式为y=kx+b(k,b为常数,k≠0),将点B(0,-1),F的坐标分别代入,得解得
∴y=x-1.
三、19.解:(1)根据一次函数的定义,得3-|m|=1,且m+2≠0,解得m=2.
∴当m=2,n为任意实数时,此函数是一次函数.
(2)根据正比例函数的定义,得3-|m|=1,n-5=0,且m+2≠0,解得m=2,n=5.
∴当m=2,n=5时,此函数是正比例函数.
点拨:一次函数y=kx+b的表达式中,k≠0,自变量的次数为1,常数项b可以为任意实数;正比例函数y=kx的表达式中,比例系数k是常数,k≠0,自变量的次数为1.
20.解:设一次函数的表达式为y=kx+b,
∵一次函数的图象与直线y=-x+1平行,∴k=-1,
∴一次函数的表达式为y=-x+b.
∵一次函数的图象经过点(8,2),
∴2=-8+b,解得b=10,
∴一次函数的表达式为y=-x+10.
21.解:(1)对于函数y1=x+1,当x=0时,y1=1.
∴将点(0,1),点(2,0)的坐标分别代入y2=ax+b中,得
解得∴y2=-x+1.
(2)由y1>0,即x+1>0,得x>-1,
由y2>0,即-x+1>0,得x<2.
故使y1>0,y2>0的x的取值范围为-1<x<2.
22.解:因为方程组的解为
所以交点A的坐标为(2,1),所以将点A的坐标代入y=ax+2,得2a+2=1,解得a=-.
又因为函数y=kx+b的图象过点A(2,1)和点B(0,-1),
所以将点A,B的坐标分别代入y=kx+b,得解得
所以这两个一次函数的表达式分别为y=-x+2,y=x-1.
23.解:(1)设1棵甲种树苗的售价为x元,1棵乙种树苗的售价为y元,根据题意得解得
答:1棵甲种树苗的售价为19元,1棵乙种树苗的售价为15元.
(2)设购买甲种树苗a棵,则购买乙种树苗(100-a)棵,总费用为w元,依题意,得w=19a+15(100-a)=4a+1
500.
∵4>0,∴w随着a的增大而增大.
∴当a取最小值时,w有最小值.
∵100-a≤2a,∴a≥.
又∵a为整数.
∴当a=34时,w最小,且w最小=4×34+1
500=1
636,此时100-a=66.
∴最省钱的购买方案为购买甲种树苗34棵,购买乙种树苗66棵,总费用为1
636元.
24.解:(1)过点P作PF⊥y轴于点F.
∵点P的横坐标是2,∴PF=2.
又∵点C(0,2),∴OC=2,
∴S△COP=OC·PF=×2×2=2.
(2)∵S△AOC=S△AOP-S△COP=6-2=4,
∴S△AOC=OA·OC=4,即×OA×2=4,
∴OA=4,∴点A的坐标是(-4,0).
设直线AP的表达式是y=kx+b,将点A,C的坐标分别代入,得
解得
∴直线AP的表达式是y=x+2.
当x=2时,y=3,即p=3.
(3)设直线BD的表达式为y=ax+c,
∴点D的坐标为(0,c),点B的坐标为.
∵S△BOP=S△DOP,
∴OD·2=OB·3,
即c·2=·3.
由题意知c≠0,∴a=-,
∴直线BD的表达式是y=-x+c.
将点P(2,3)的坐标代入得3=-×2+c,解得c=6,∴直线BD的表达式是y=-x+6.
25.解:(1)a=4.5,甲车的速度为=60(千米/时).
(2)设乙车开始的速度为v千米/时,则4v+(7-4.5)×(v-50)=460,解得v=90,4v=360,
则D(4,360),E(4.5,360).
设直线EF对应的函数表达式为y=kx+b,把点E(4.5,360),点F(7,460)的坐标分别代入,得
解得
所以线段EF所表示的y与x之间的函数表达式为y=40x+180(4.5≤x≤7).
(3)60×=40(千米),则C(0,40),设直线CF对应的函数表达式为y=mx+n.
把点C(0,40),点F(7,460)的坐标分别代入,得解得
所以直线CF对应的函数表达式为y=60x+40,易得线段OD对应的函数表达式为y=90x(0≤x≤4),设CF交OD于点G,易得G,当0≤x≤时,60x+40-90x=15,解得x=;
当
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
