高一【数学(人教A版)】4.2指数函数的概念-课件1(35张PPT)
文档属性
| 名称 | 高一【数学(人教A版)】4.2指数函数的概念-课件1(35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 427.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 21:22:55 | ||
图片预览










文档简介
指数函数的概念
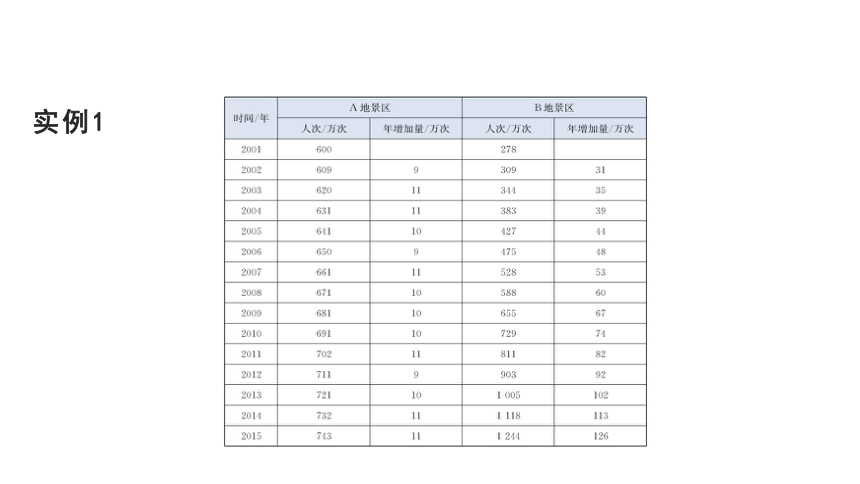
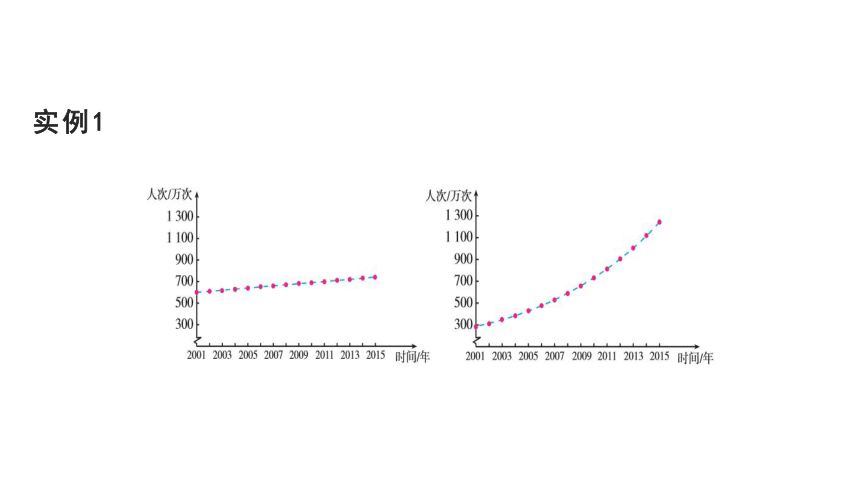
实例1
实例1
实例1
增长率约为1.11-1=0.11,是一个常数.
指数增长
实例1
你能否用函数解析式刻画B地景区游客人次随时间指数增长的变化规律?
实例1
实例2
当生物死后,它机体内原有的碳14含量会按确定的比率衰减(称为衰减率),大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”. 按照上述变化规律,死亡生物体内碳14含量与死亡年数之间有怎样的关系?
实例2
实际上科学研究表明,宇宙射线在大气中能产生包括碳14在内的放射性物质.碳14的衰减非常有规律,其准确性可以称为自然界的“准确时钟”,动植物在生长过程中衰减的碳14,可以通过与大气的相互作用得到补充,所以活着的动植物体内的碳14含量不变.死亡后的动植物停止了与外界的相互作用,体内原有的碳14按确定的规律衰减,半衰期为5730年,这也是考古中常用碳14来推断年代的原因.
实例2
指数衰减
实际上科学研究表明,宇宙射线在大气中能产生包括碳14在内的放射性物质.碳14的衰减非常有规律,其准确性可以称为自然界的“准确时钟”,动植物在生长过程中衰减的碳14,可以通过与大气的相互作用得到补充,所以活着的动植物体内的碳14含量不变.死亡后的动植物停止了与外界的相互作用,体内原有的碳14按确定的规律衰减,半衰期为5730年,这也是考古中常用碳14来推断年代的原因.
实例2
死亡生物体内碳14含量的年衰减率为多少?能否用函数解析式刻画死亡生物体内碳14含量随时间的变化情况?
实例2
设死亡生物体内碳14含量的年衰减率为p,刚死亡时碳14含量为1个单位,
实例2
设死亡生物体内碳14含量的年衰减率为p,刚死亡时碳14含量为1个单位,
实例2
所以设生物死亡年数为x,死亡生物体内碳14含量为y,则
问题
比较上述两个实例,B地景区游客人次增长与碳14衰减,它们所反映的变化规律有什么共同特征?
问题
比较上述两个实例,B地景区游客人次增长与碳14衰减,它们所反映的变化规律有什么共同特征?
从数据看,它们的变化率(增长率、衰减率)是常数.
问题
比较上述两个实例,B地景区游客人次增长与碳14衰减,它们所反映的变化规律有什么共同特征?
从数据看,它们的变化率(增长率、衰减率)是常数.
问题
比较上述两个实例,B地景区游客人次增长与碳14衰减,它们所反映的变化规律有什么共同特征?
从数据看,它们的变化率(增长率、衰减率)是常数.
从解析式看,如果用a代替底数,则它们都是y=ax的形式.
指数函数
一般地,函数y=ax(a>0且a≠1)叫做指数函数,其中x为自变量,定义域为R.
指数函数
一般地,函数y=ax(a>0且a≠1)叫做指数函数,其中x为自变量,定义域为R.
在指数函数中,当x∈N时,y=ax(a>1)还可以表示为y=(1+p)x,其中p(p>0)表示增长率;y=ax(00)表示衰减率.
因此指数函数是刻画呈指数增长或指数衰减变化规律的函数模型.
例1
已知函数f(x) =????????(a>0且a≠1),且f(3)=π,求f(0), f(1), f(-3)的值.
?
例1
已知函数f(x) =????????(a>0且a≠1),且f(3)=π,求f(0), f(1), f(-3)的值.
解:由f(3)=π可知a3 =π,
解得a=π13,
于是f(x) =π????3.
所以f(0)=1, f(1) =π13, f(-3) =π?1.
?
练习1
下列图象中有可能表示指数函数的图象是( )
练习1
下列图象中有可能表示指数函数的图象是( )
答案:C
练习2
已知函数y=f(x), x∈R,且
求函数y=f(x)的一个解析式.
练习2
已知函数y=f(x), x∈R,且
求函数y=f(x)的一个解析式.
解:由题意可知函数f(x)以4为增长比例呈指数增长,
又因为f(0)=3,即初始量为3,
所以f(x)=3×4????.
?
例2
(1)在实例1中,如果平均每位游客出游一次可给当地带来1000元门票之外的收入,A地景区的门票价格为150元,比较这15年间A,B两地旅游收入变化情况.
(2)在实例2中,某生物死亡10000年后,它体内碳14的含量衰减为原来的百分之几?
例2
(1)在实例1中,如果平均每位游客出游一次可给当地带来1000元门票之外的收入,A地景区的门票价格为150元,比较这15年间A,B两地旅游收入变化情况.
解:设x年后A,B两地的旅游收入分别为f(x)和g(x),则
例2
(1)在实例1中,如果平均每位游客出游一次可给当地带来1000元门票之外的收入,A地景区的门票价格为150元,比较这15年间A,B两地旅游收入变化情况.
解:设x年后A,B两地的旅游收入分别为f(x)和g(x),则
例2
(1)在实例1中,如果平均每位游客出游一次可给当地带来1000元门票之外的收入,A地景区的门票价格为150元,比较这15年间A,B两地旅游收入变化情况.
解:设x年后A,B两地的旅游收入分别为f(x)和g(x),则
例2
(1)在实例1中,如果平均每位游客出游一次可给当地带来1000元门票之外的收入,A地景区的门票价格为150元,比较这15年间A,B两地旅游收入变化情况.
解:设x年后A,B两地的旅游收入分别为f(x)和g(x),则
例2
(2)在实例2中,某生物死亡10000年后,它体内碳14的含量衰减为原来的百分之几?
解:设生物死时体内碳14含量为1个单位,x年后含量为h(x),则
例2
(2)在实例2中,某生物死亡10000年后,它体内碳14的含量衰减为原来的百分之几?
解:设生物死时体内碳14含量为1个单位,x年后含量为h(x),则
例2
(2)在实例2中,某生物死亡10000年后,它体内碳14的含量衰减为原来的百分之几?
解:设生物死时体内碳14含量为1个单位,x年后含量为h(x),则
所以x=10000时,利用计算工具可得h(10000)≈0.30.
所以它体内碳14的含量衰减为原来的30%.
小结
通过本节课的学习,你是否理解了指数增长和指数衰减的变化规律和特点,你是否能够理解指数函数的概念,能够利用指数概念解决简单的实际问题.
课后作业
1.课本115页阅读与思考
实例1
实例1
实例1
增长率约为1.11-1=0.11,是一个常数.
指数增长
实例1
你能否用函数解析式刻画B地景区游客人次随时间指数增长的变化规律?
实例1
实例2
当生物死后,它机体内原有的碳14含量会按确定的比率衰减(称为衰减率),大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”. 按照上述变化规律,死亡生物体内碳14含量与死亡年数之间有怎样的关系?
实例2
实际上科学研究表明,宇宙射线在大气中能产生包括碳14在内的放射性物质.碳14的衰减非常有规律,其准确性可以称为自然界的“准确时钟”,动植物在生长过程中衰减的碳14,可以通过与大气的相互作用得到补充,所以活着的动植物体内的碳14含量不变.死亡后的动植物停止了与外界的相互作用,体内原有的碳14按确定的规律衰减,半衰期为5730年,这也是考古中常用碳14来推断年代的原因.
实例2
指数衰减
实际上科学研究表明,宇宙射线在大气中能产生包括碳14在内的放射性物质.碳14的衰减非常有规律,其准确性可以称为自然界的“准确时钟”,动植物在生长过程中衰减的碳14,可以通过与大气的相互作用得到补充,所以活着的动植物体内的碳14含量不变.死亡后的动植物停止了与外界的相互作用,体内原有的碳14按确定的规律衰减,半衰期为5730年,这也是考古中常用碳14来推断年代的原因.
实例2
死亡生物体内碳14含量的年衰减率为多少?能否用函数解析式刻画死亡生物体内碳14含量随时间的变化情况?
实例2
设死亡生物体内碳14含量的年衰减率为p,刚死亡时碳14含量为1个单位,
实例2
设死亡生物体内碳14含量的年衰减率为p,刚死亡时碳14含量为1个单位,
实例2
所以设生物死亡年数为x,死亡生物体内碳14含量为y,则
问题
比较上述两个实例,B地景区游客人次增长与碳14衰减,它们所反映的变化规律有什么共同特征?
问题
比较上述两个实例,B地景区游客人次增长与碳14衰减,它们所反映的变化规律有什么共同特征?
从数据看,它们的变化率(增长率、衰减率)是常数.
问题
比较上述两个实例,B地景区游客人次增长与碳14衰减,它们所反映的变化规律有什么共同特征?
从数据看,它们的变化率(增长率、衰减率)是常数.
问题
比较上述两个实例,B地景区游客人次增长与碳14衰减,它们所反映的变化规律有什么共同特征?
从数据看,它们的变化率(增长率、衰减率)是常数.
从解析式看,如果用a代替底数,则它们都是y=ax的形式.
指数函数
一般地,函数y=ax(a>0且a≠1)叫做指数函数,其中x为自变量,定义域为R.
指数函数
一般地,函数y=ax(a>0且a≠1)叫做指数函数,其中x为自变量,定义域为R.
在指数函数中,当x∈N时,y=ax(a>1)还可以表示为y=(1+p)x,其中p(p>0)表示增长率;y=ax(0
因此指数函数是刻画呈指数增长或指数衰减变化规律的函数模型.
例1
已知函数f(x) =????????(a>0且a≠1),且f(3)=π,求f(0), f(1), f(-3)的值.
?
例1
已知函数f(x) =????????(a>0且a≠1),且f(3)=π,求f(0), f(1), f(-3)的值.
解:由f(3)=π可知a3 =π,
解得a=π13,
于是f(x) =π????3.
所以f(0)=1, f(1) =π13, f(-3) =π?1.
?
练习1
下列图象中有可能表示指数函数的图象是( )
练习1
下列图象中有可能表示指数函数的图象是( )
答案:C
练习2
已知函数y=f(x), x∈R,且
求函数y=f(x)的一个解析式.
练习2
已知函数y=f(x), x∈R,且
求函数y=f(x)的一个解析式.
解:由题意可知函数f(x)以4为增长比例呈指数增长,
又因为f(0)=3,即初始量为3,
所以f(x)=3×4????.
?
例2
(1)在实例1中,如果平均每位游客出游一次可给当地带来1000元门票之外的收入,A地景区的门票价格为150元,比较这15年间A,B两地旅游收入变化情况.
(2)在实例2中,某生物死亡10000年后,它体内碳14的含量衰减为原来的百分之几?
例2
(1)在实例1中,如果平均每位游客出游一次可给当地带来1000元门票之外的收入,A地景区的门票价格为150元,比较这15年间A,B两地旅游收入变化情况.
解:设x年后A,B两地的旅游收入分别为f(x)和g(x),则
例2
(1)在实例1中,如果平均每位游客出游一次可给当地带来1000元门票之外的收入,A地景区的门票价格为150元,比较这15年间A,B两地旅游收入变化情况.
解:设x年后A,B两地的旅游收入分别为f(x)和g(x),则
例2
(1)在实例1中,如果平均每位游客出游一次可给当地带来1000元门票之外的收入,A地景区的门票价格为150元,比较这15年间A,B两地旅游收入变化情况.
解:设x年后A,B两地的旅游收入分别为f(x)和g(x),则
例2
(1)在实例1中,如果平均每位游客出游一次可给当地带来1000元门票之外的收入,A地景区的门票价格为150元,比较这15年间A,B两地旅游收入变化情况.
解:设x年后A,B两地的旅游收入分别为f(x)和g(x),则
例2
(2)在实例2中,某生物死亡10000年后,它体内碳14的含量衰减为原来的百分之几?
解:设生物死时体内碳14含量为1个单位,x年后含量为h(x),则
例2
(2)在实例2中,某生物死亡10000年后,它体内碳14的含量衰减为原来的百分之几?
解:设生物死时体内碳14含量为1个单位,x年后含量为h(x),则
例2
(2)在实例2中,某生物死亡10000年后,它体内碳14的含量衰减为原来的百分之几?
解:设生物死时体内碳14含量为1个单位,x年后含量为h(x),则
所以x=10000时,利用计算工具可得h(10000)≈0.30.
所以它体内碳14的含量衰减为原来的30%.
小结
通过本节课的学习,你是否理解了指数增长和指数衰减的变化规律和特点,你是否能够理解指数函数的概念,能够利用指数概念解决简单的实际问题.
课后作业
1.课本115页阅读与思考
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
