高一【数学(人教A版)】4.2指数函数的应用-课件1(21张PPT)
文档属性
| 名称 | 高一【数学(人教A版)】4.2指数函数的应用-课件1(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 562.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 21:26:40 | ||
图片预览







文档简介
指数函数的应用
复习回顾
一、指数函数的定义
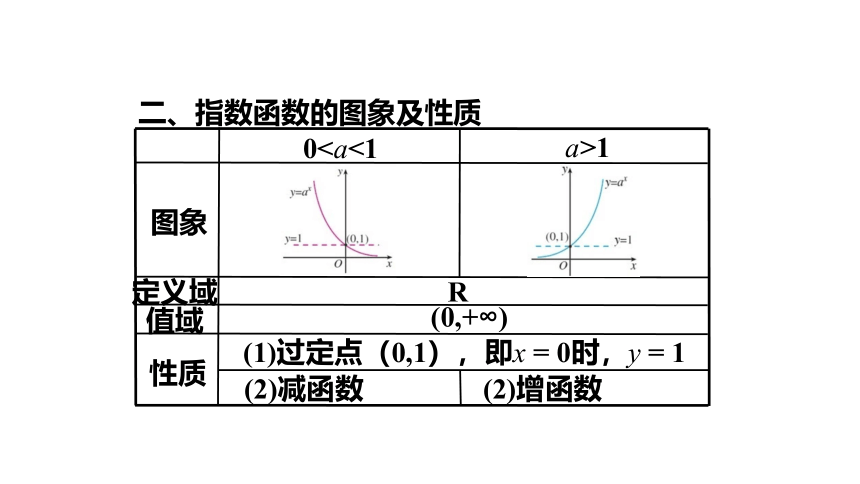
二、指数函数的图象及性质
0图象
定义域
值域
性质
a>1
R
(0,+∞)
(1)过定点(0,1),即x = 0时,y = 1
(2)减函数
(2)增函数
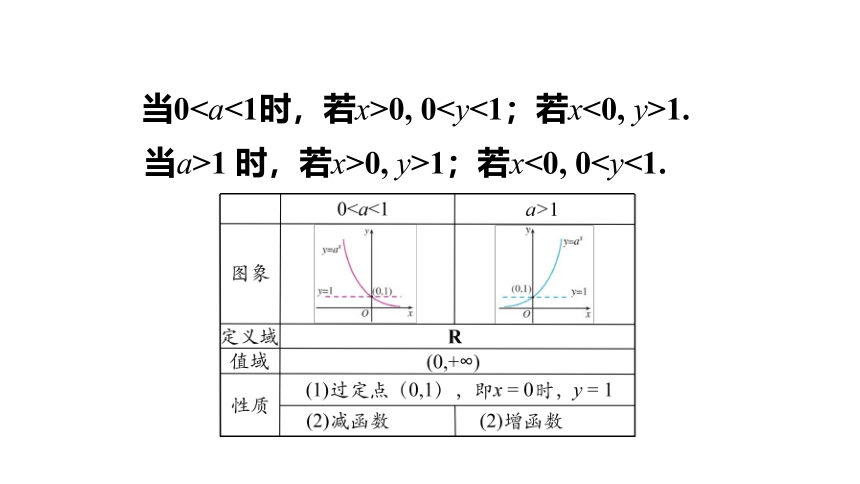
当00, 01.
当a>1 时,若x>0, y>1;若x<0, 0例题讲解
2.5 3
>1
增函数
2.5<3
1.72.5<1.73
解:1.72.5和1.73可以看作函数y=1.7x当x
分别取 和 时所对应的两个函数值.
解:
解:由指数函数y=1.7x和y=0.9x的单调性知
1.70.3>1.70
=1,
0.93.1<0.90
=1.
所以1.70.3>1> 0.93.1,
也就是1.70.3>0.93.1.
练习:比较下列各题中两个值的大小:
练习:比较下列各题中两个值的大小:
答案:
思考:比较两个幂的大小的方法有哪些?
(1)底数相同,但指数不同的幂比大小;
(2)底数不同,但指数相同的幂比大小;
(3)底数不同,且指数不同的幂比大小.
用函数观点解决问题.
解:(1)该城市人口经过20年约为
10万人,经过40年约为20万人,
即由10万人口增加到20万人口所用的时间约
为20年,
所以该城市人口每翻一番所需的时间
约为20年.
解:(2)因为倍增期为20年,
所以每经过20年,人口将翻一番.
因此,从80万人开始,经过20年,
该城市人口大约会增长到160万人.
巩固提升
(1)求该函数的解析式,并画出图象;
∴b= -1,
.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
y
①列表:
0 1 2 3 4
②描点;
③连线.
偶函数!
巩固提升
(2)判断该函数的奇偶性和单调性.
解:
1.比较两个幂的大小的方法:
(1)底数相同,但指数不同的幂比大小;
(2)底数不同,但指数相同的幂比大小;
(3)底数不同,且指数不同的幂比大小.
课堂小结
用函数观点解决问题.
概念——图象——性质
作业:
教科书习题4.2 3,6,7.
复习回顾
一、指数函数的定义
二、指数函数的图象及性质
0
定义域
值域
性质
a>1
R
(0,+∞)
(1)过定点(0,1),即x = 0时,y = 1
(2)减函数
(2)增函数
当0
当a>1 时,若x>0, y>1;若x<0, 0
2.5 3
>1
增函数
2.5<3
1.72.5<1.73
解:1.72.5和1.73可以看作函数y=1.7x当x
分别取 和 时所对应的两个函数值.
解:
解:由指数函数y=1.7x和y=0.9x的单调性知
1.70.3>1.70
=1,
0.93.1<0.90
=1.
所以1.70.3>1> 0.93.1,
也就是1.70.3>0.93.1.
练习:比较下列各题中两个值的大小:
练习:比较下列各题中两个值的大小:
答案:
思考:比较两个幂的大小的方法有哪些?
(1)底数相同,但指数不同的幂比大小;
(2)底数不同,但指数相同的幂比大小;
(3)底数不同,且指数不同的幂比大小.
用函数观点解决问题.
解:(1)该城市人口经过20年约为
10万人,经过40年约为20万人,
即由10万人口增加到20万人口所用的时间约
为20年,
所以该城市人口每翻一番所需的时间
约为20年.
解:(2)因为倍增期为20年,
所以每经过20年,人口将翻一番.
因此,从80万人开始,经过20年,
该城市人口大约会增长到160万人.
巩固提升
(1)求该函数的解析式,并画出图象;
∴b= -1,
.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
y
①列表:
0 1 2 3 4
②描点;
③连线.
偶函数!
巩固提升
(2)判断该函数的奇偶性和单调性.
解:
1.比较两个幂的大小的方法:
(1)底数相同,但指数不同的幂比大小;
(2)底数不同,但指数相同的幂比大小;
(3)底数不同,且指数不同的幂比大小.
课堂小结
用函数观点解决问题.
概念——图象——性质
作业:
教科书习题4.2 3,6,7.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
