高一【数学(人教A版)】4.2指数函数的图象和性质-课件1(37张PPT)
文档属性
| 名称 | 高一【数学(人教A版)】4.2指数函数的图象和性质-课件1(37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 819.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 21:22:34 | ||
图片预览









文档简介
指数函数的图象和性质
一般地,函数 y = ax(a>0,且 a ≠1)叫做指数函数 (exponential function ),其中指数 x 是自变量,定义域是R.
概念复习
背景——概念——图象和性质——应用
函数研究的一般思路
先做出具体函数的图象,然后通过观察、比较不同函数的图象,最后归纳它们共同的特征.
研究函数性质的三步曲
指数函数的图象和性质
研究指数函数 y=2x .
指数函数的图象和性质
研究指数函数 y=2x .
定义域是R;
指数函数的图象和性质
研究指数函数 y=2x .
定义域是R;
值域是(0,+∞)?
指数函数的图象和性质
研究指数函数 y=2x .
定义域是R;
值域是(0,+∞)?
不具有奇偶性;
指数函数的图象和性质
研究指数函数 y=2x .
定义域是R;
值域是(0,+∞)?
不具有奇偶性;
单调性?
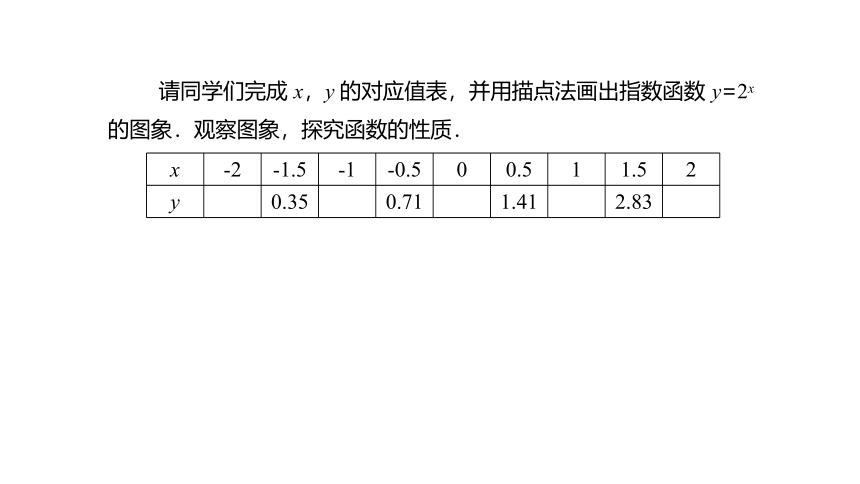
请同学们完成 x,y 的对应值表,并用描点法画出指数函数 y=2x 的图象.观察图象,探究函数的性质.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
y
0.35
0.71
1.41
2.83
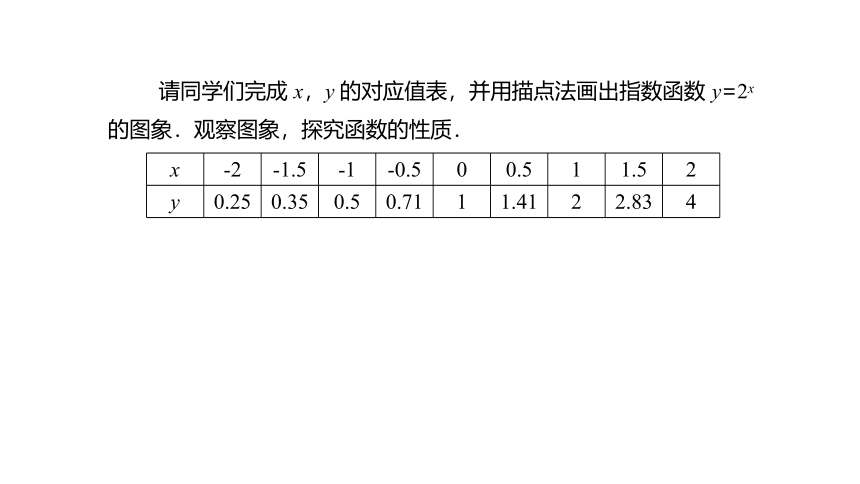
请同学们完成 x,y 的对应值表,并用描点法画出指数函数 y=2x 的图象.观察图象,探究函数的性质.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
y
0.25
0.35
0.5
0.71
1
1.41
2
2.83
4
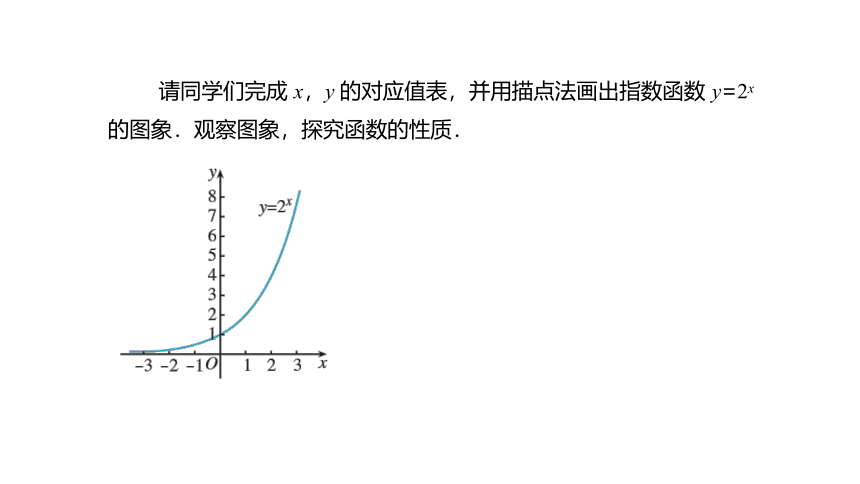
请同学们完成 x,y 的对应值表,并用描点法画出指数函数 y=2x 的图象.观察图象,探究函数的性质.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
y=2x
定义域
R
值域
(0,+∞)
单调性
增函数
请同学们完成 x,y 的对应值表,并用描点法画出指数函数 y=2x 的图象.观察图象,探究函数的性质.
请同学们画出指数函数 ?????????的图象.观察图象,探究函数的性质.
?
请同学们画出指数函数 ?????????的图象.观察图象,探究函数的性质.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
定义域
R
值域
(0,+∞)
单调性
减函数
问题1 你是如何画出函数 的图象.
问题1 你是如何画出函数 的图象.
方法1 描点法画图.
问题1 你是如何画出函数 的图象.
方法1 描点法画图.
方法2 利用对称性画图.
因为 ,点(x,y)与点(-x,y)关于y轴对称,所以函数 y=2x 图象上任意一点 P(x,y)关于 y 轴的对称点P1(-x,y)都在函数 的图象上,反之亦然.
问题1 你是如何画出函数 的图象.
因为 ,点(x,y)与点(-x,y)关于y轴对称,所以函数 y=2x 图象上任意一点 P(x,y)关于 y 轴的对称点P1(-x,y)都在函数 的图象上,反之亦然.所以可利用函数 y=2x 的图象,画出函数 的图象.
问题1 你是如何画出函数 的图象.
底数互为倒数的两个指数函数的图象关于 y 轴对称.根据这种对称性,就可以利用一个函数的图象,画出另一个函数的图象.
问题1 你是如何画出函数 的图象.
将指数函数 y=ax 的图象按底数 a 的取值,分作 a>1 和 0 将指数函数 y=ax 的图象按底数 a 的取值,分作 a>1 和 0{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
y=2x
定义域
R
R
值域
(0,+∞)
(0,+∞)
单调性
增函数
减函数
研究指数函数 y=ax (a>1)的图象和性质.
请同学们画出指数函数 y=3x 和 y=4x 的图象,探究它们的性质.
研究指数函数 y=ax (a>1)的图象和性质.
请同学们画出指数函数 y=3x 和 y=4x 的图象,探究它们的性质.
研究指数函数 y=ax (a>1)的图象和性质.
请同学们画出指数函数 y=3x 和 y=4x 的图象,探究它们的性质.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
y=3x
y=4x
定义域
R
R
值域
(0,+∞)
(0,+∞)
单调性
增函数
增函数
研究指数函数 y=ax (0 请同学们利用对称性画出指数函数 和 的图象,探究它们的性质.
研究指数函数 y=ax (0 请同学们利用对称性画出指数函数 和 的图象,探究它们的性质.
研究指数函数 y=ax (0 请同学们利用对称性画出指数函数 和 的图象,探究它们的性质.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
定义域
R
R
值域
(0,+∞)
(0,+∞)
单调性
减函数
减函数
问题2 观察这些图象的位置、公共点和变化趋势,它们有哪些共性?
问题2 观察这些图象的位置、公共点和变化趋势,它们有哪些共性?
(1)图象都过点(0,1).
(2)定义域都是(-∞,+∞),值域都是(0,+∞).
(3)当01时,函数图象均呈上升趋势,即函数为增函数.
问题3 这几个函数的图象是否能代表一般的指数函数的图象?我们得到的性质是否推广到一般的指数函数的性质?
问题3 这几个函数的图象是否能代表一般的指数函数的图象?我们得到的性质是否推广到一般的指数函数的性质?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0a>1
图象
定义域
值域
性质
指数函数 y=ax ( a>0,且 a ≠ 1)的图象和性质 .
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0a>1
图象
定义域
R
值域
(0,+∞)
性质
(1)过定点(0,1),即x=0时,y=1
(2)减函数
指数函数 y=ax ( a>0,且 a ≠ 1)的图象和性质 .
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0a>1
图象
定义域
R
值域
(0,+∞)
性质
(1)过定点(0,1),即x=0时,y=1
(2)减函数
(2)增函数
指数函数 y=ax ( a>0,且 a ≠ 1)的图象和性质 .
课堂小结
在最后,我们回顾一下这堂课的内容,请同学们思考以下问题:
(1)在本节课,你学习了哪些知识?
(2)在研究指数函数的图象和性质的过程中,你用到了什么方法?
一般地,函数 y = ax(a>0,且 a ≠1)叫做指数函数 (exponential function ),其中指数 x 是自变量,定义域是R.
概念复习
背景——概念——图象和性质——应用
函数研究的一般思路
先做出具体函数的图象,然后通过观察、比较不同函数的图象,最后归纳它们共同的特征.
研究函数性质的三步曲
指数函数的图象和性质
研究指数函数 y=2x .
指数函数的图象和性质
研究指数函数 y=2x .
定义域是R;
指数函数的图象和性质
研究指数函数 y=2x .
定义域是R;
值域是(0,+∞)?
指数函数的图象和性质
研究指数函数 y=2x .
定义域是R;
值域是(0,+∞)?
不具有奇偶性;
指数函数的图象和性质
研究指数函数 y=2x .
定义域是R;
值域是(0,+∞)?
不具有奇偶性;
单调性?
请同学们完成 x,y 的对应值表,并用描点法画出指数函数 y=2x 的图象.观察图象,探究函数的性质.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
y
0.35
0.71
1.41
2.83
请同学们完成 x,y 的对应值表,并用描点法画出指数函数 y=2x 的图象.观察图象,探究函数的性质.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
y
0.25
0.35
0.5
0.71
1
1.41
2
2.83
4
请同学们完成 x,y 的对应值表,并用描点法画出指数函数 y=2x 的图象.观察图象,探究函数的性质.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
y=2x
定义域
R
值域
(0,+∞)
单调性
增函数
请同学们完成 x,y 的对应值表,并用描点法画出指数函数 y=2x 的图象.观察图象,探究函数的性质.
请同学们画出指数函数 ?????????的图象.观察图象,探究函数的性质.
?
请同学们画出指数函数 ?????????的图象.观察图象,探究函数的性质.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
定义域
R
值域
(0,+∞)
单调性
减函数
问题1 你是如何画出函数 的图象.
问题1 你是如何画出函数 的图象.
方法1 描点法画图.
问题1 你是如何画出函数 的图象.
方法1 描点法画图.
方法2 利用对称性画图.
因为 ,点(x,y)与点(-x,y)关于y轴对称,所以函数 y=2x 图象上任意一点 P(x,y)关于 y 轴的对称点P1(-x,y)都在函数 的图象上,反之亦然.
问题1 你是如何画出函数 的图象.
因为 ,点(x,y)与点(-x,y)关于y轴对称,所以函数 y=2x 图象上任意一点 P(x,y)关于 y 轴的对称点P1(-x,y)都在函数 的图象上,反之亦然.所以可利用函数 y=2x 的图象,画出函数 的图象.
问题1 你是如何画出函数 的图象.
底数互为倒数的两个指数函数的图象关于 y 轴对称.根据这种对称性,就可以利用一个函数的图象,画出另一个函数的图象.
问题1 你是如何画出函数 的图象.
将指数函数 y=ax 的图象按底数 a 的取值,分作 a>1 和 0
y=2x
定义域
R
R
值域
(0,+∞)
(0,+∞)
单调性
增函数
减函数
研究指数函数 y=ax (a>1)的图象和性质.
请同学们画出指数函数 y=3x 和 y=4x 的图象,探究它们的性质.
研究指数函数 y=ax (a>1)的图象和性质.
请同学们画出指数函数 y=3x 和 y=4x 的图象,探究它们的性质.
研究指数函数 y=ax (a>1)的图象和性质.
请同学们画出指数函数 y=3x 和 y=4x 的图象,探究它们的性质.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
y=3x
y=4x
定义域
R
R
值域
(0,+∞)
(0,+∞)
单调性
增函数
增函数
研究指数函数 y=ax (0
研究指数函数 y=ax (0
研究指数函数 y=ax (0
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
定义域
R
R
值域
(0,+∞)
(0,+∞)
单调性
减函数
减函数
问题2 观察这些图象的位置、公共点和变化趋势,它们有哪些共性?
问题2 观察这些图象的位置、公共点和变化趋势,它们有哪些共性?
(1)图象都过点(0,1).
(2)定义域都是(-∞,+∞),值域都是(0,+∞).
(3)当0
问题3 这几个函数的图象是否能代表一般的指数函数的图象?我们得到的性质是否推广到一般的指数函数的性质?
问题3 这几个函数的图象是否能代表一般的指数函数的图象?我们得到的性质是否推广到一般的指数函数的性质?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0
图象
定义域
值域
性质
指数函数 y=ax ( a>0,且 a ≠ 1)的图象和性质 .
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0
图象
定义域
R
值域
(0,+∞)
性质
(1)过定点(0,1),即x=0时,y=1
(2)减函数
指数函数 y=ax ( a>0,且 a ≠ 1)的图象和性质 .
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0
图象
定义域
R
值域
(0,+∞)
性质
(1)过定点(0,1),即x=0时,y=1
(2)减函数
(2)增函数
指数函数 y=ax ( a>0,且 a ≠ 1)的图象和性质 .
课堂小结
在最后,我们回顾一下这堂课的内容,请同学们思考以下问题:
(1)在本节课,你学习了哪些知识?
(2)在研究指数函数的图象和性质的过程中,你用到了什么方法?
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
