人教版 九年级数学上册 第23章 23.1 图形的旋转同步测试题(word版含答案)
文档属性
| 名称 | 人教版 九年级数学上册 第23章 23.1 图形的旋转同步测试题(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 00:00:00 | ||
图片预览



文档简介
人教版 九年级数学上册 23.1 图形的旋转
一、选择题(本大题共8道小题)
1. 在平面直角坐标系中,点P(-4,2)向右平移7个单位长度得到点P1,点P1绕原点逆时针旋转90°得到点P2,则点P2的坐标是( )
A.(-2,3) B.(-3,2)
C.(2,-3) D.(3,-2)
2. 把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为 ( )
A.30° B.90° C.120° D.180°
3. 如图所示,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心是 ( )
A.点A B.点B
C.点C D.点D
4. 观察图,其中可以看成是由“基本图案”通过旋转形成的共有( )
A.1个 B.2个 C.3个 D.4个
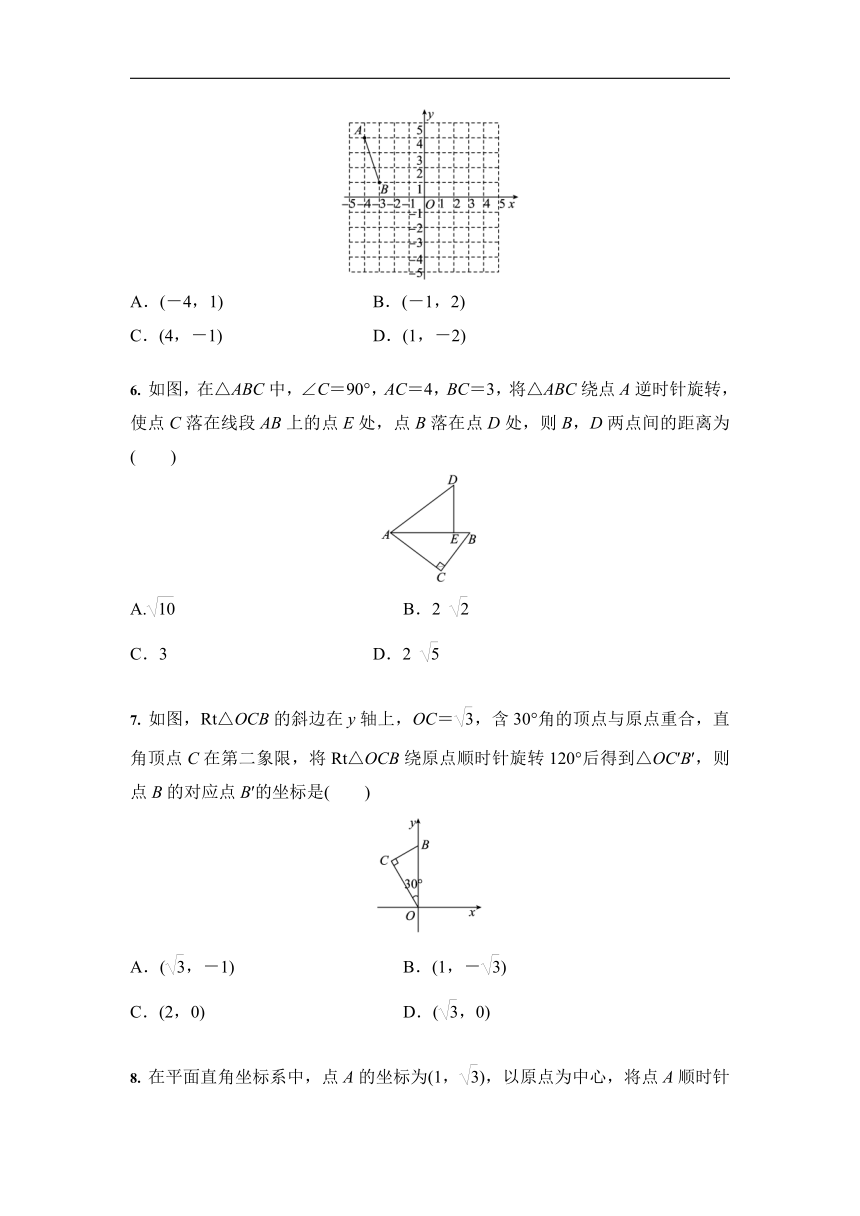
5. 如图,将线段AB先向右平移5个单位长度,再将所得线段绕原点顺时针旋转90°,得到线段A′B′,则点B的对应点B′的坐标是( )
A.(-4,1) B.(-1,2)
C.(4,-1) D.(1,-2)
6. 如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为( )
A. B.2
C.3 D.2
7. 如图,Rt△OCB的斜边在y轴上,OC=,含30°角的顶点与原点重合,直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′,则点B的对应点B′的坐标是( )
A.(,-1) B.(1,-)
C.(2,0) D.(,0)
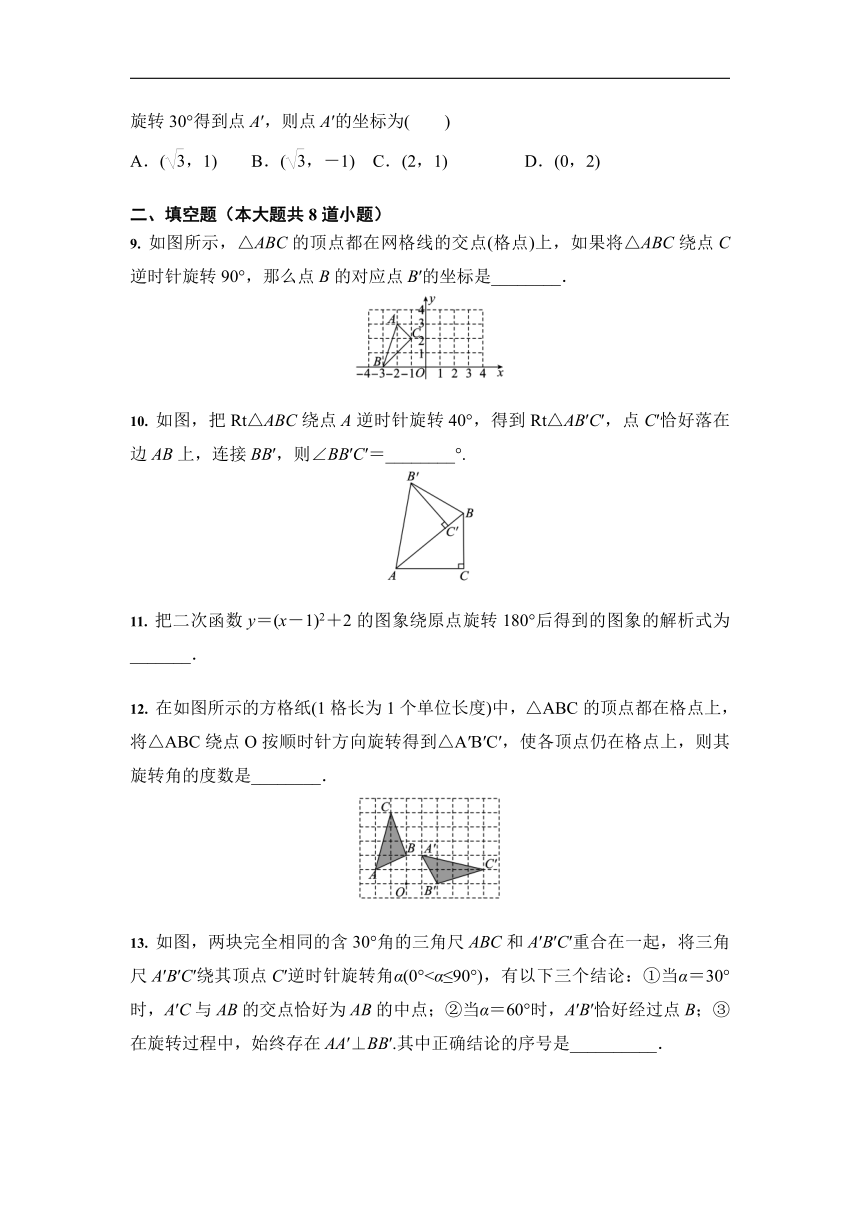
8. 在平面直角坐标系中,点A的坐标为(1,),以原点为中心,将点A顺时针旋转30°得到点A′,则点A′的坐标为( )
A.(,1) B.(,-1) C.(2,1) D.(0,2)
二、填空题(本大题共8道小题)
9. 如图所示,△ABC的顶点都在网格线的交点(格点)上,如果将△ABC绕点C逆时针旋转90°,那么点B的对应点B′的坐标是________.
10. 如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=________°.
11. 把二次函数y=(x-1)2+2的图象绕原点旋转180°后得到的图象的解析式为_______.
12. 在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A′B′C′,使各顶点仍在格点上,则其旋转角的度数是________.
13. 如图,两块完全相同的含30°角的三角尺ABC和A′B′C′重合在一起,将三角尺A′B′C′绕其顶点C′逆时针旋转角α(0°<α≤90°),有以下三个结论:①当α=30°时,A′C与AB的交点恰好为AB的中点;②当α=60°时,A′B′恰好经过点B;③在旋转过程中,始终存在AA′⊥BB′.其中正确结论的序号是__________.
14. 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为________.
15. 如图,在△ABC中,∠BAC=90°,AB=AC=10 cm,D为△ABC内一点,∠BAD=15°,AD=6 cm,连接BD,将△ABD绕点A逆时针旋转,使AB与AC重合,点D的对应点为点E,连接DE,DE交AC于点F,则CF的长为________ cm.
16. 如图,将Rt△ABC的斜边AB绕点A顺时针旋转α(0°<α<90°)得到AE,直角边AC绕点A逆时针旋转β(0°<β<90°)得到AF,连接EF,若AB=3,AC=2,且α+β=∠B,则EF=________.
三、解答题(本大题共4道小题)
17. 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与点A,B不重合),连接CD,将线段CD绕点C逆时针旋转90°得到线段CE,连接DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
(2)当AD=BF时,求∠BEF的度数.
18. 如图,在正方形网格中,每个小正方形的边长都是1个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,4),B(1,1),C(3,1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC绕点O逆时针旋转90°后得到的△A2B2C2;
(3)在(2)的条件下,求点A所经过的路径长(结果保留π).
19. (1)如图 (a),在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;
②若∠A=90°,探索线段BE,CF,EF之间的数量关系,并加以证明.
(2)如图(b),在四边形ABDC中,∠B+∠C=180°,BD=CD,∠BDC=120°,以D为顶点作一个60°的角,角的两边分别交AB,AC于E,F两点,连接EF,探索线段BE,CF,EF之间的数量关系,并加以证明.
20. 已知:如图,在四边形ABCD中,∠ADC=60°,∠ABC=30°,AD=CD.
求证:BD2=AB2+BC2.
人教版 九年级数学上册 23.1 图形的旋转 同步训练-答案
一、选择题(本大题共8道小题)
1. 【答案】A [解析] 点P(-4,2)向右平移7个单位长度得到点P1(3,2),点P1绕原点逆时针旋转90°得到点P2(-2,3).故选A.
2. 【答案】C
3. 【答案】B [解析] 旋转中心到对应点的距离相等.
4. 【答案】D
5. 【答案】D
6. 【答案】A [解析] ∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB=5.
∵将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,
∴AE=4,DE=3,∴BE=1.
在Rt△BED中,BD==.故选A.
7. 【答案】A
8. 【答案】A [解析] 如图,过点A作AE⊥y轴于点E,过点A′作A′F⊥x轴于点F,
∴∠AEO=∠A′FO=90°.
∵点A的坐标为(1,),∴AE=1,OE=,
∴OA=2,∠AOE=30°,由旋转可知∠AOA′=30°,OA′=OA=2,∴∠A′OF=90°-30°-30°=30°,∴A′F=OA′=1,OF=,∴A′(,1).
故选A.
二、填空题(本大题共8道小题)
9. 【答案】(1,0)
10. 【答案】20 [解析] ∵AB=AB′,∠BAB′=40°,
∴∠ABB′=70°.∵B′C′⊥AB,∴∠BB′C′=20°.
11. 【答案】y=-x2-2x-3 [解析] 旋转前二次项的系数a=1,抛物线的顶点坐标是(1,2),旋转后二次项的系数a=-1,抛物线的顶点坐标是(-1,-2),∴新抛物线的解析式为y=-(x+1)2-2,即y=-x2-2x-3.
12. 【答案】90° [解析] 找到一组对应点A,A′,并将其与旋转中心连接起来,确定旋转角,进而得到旋转角的度数为90°.
13. 【答案】①②③
14. 【答案】18 [解析] 如图.∵∠BAD=∠BCD=90°,∴∠B+∠ADC=180°.又∵AB=AD,∴将△ABC绕点A逆时针旋转90°后点B与点D重合,点C的对应点E落在CD的延长线上,∴AE=AC=6,∠CAE=90°,∴S四边形ABCD=S△ACE=AC·AE=×6×6=18.
15. 【答案】(10-2 ) [解析] 如图,过点A作AG⊥DE于点G.由旋转知,AD=AE,∠DAE=90°,∠CAE=∠BAD=15°,
∴∠AED=∠ADG=45°,
∴∠AFD=∠AED+∠CAE=60°.
在Rt△ADG中,AG=DG==3 (cm).
在Rt△AFG中,GF==(cm),AF=2FG=2 (cm),
∴CF=AC-AF=(10-2 )cm.
16. 【答案】 [解析] ∵α+β=∠B,∴∠EAF=∠BAC+∠B=90°,∴△AEF是直角三角形,且AE=AB=3,AF=AC=2,∴EF==.
三、解答题(本大题共4道小题)
17. 【答案】
解:(1)证明:由题意可知,CD=CE,∠DCE=90°.
∵∠ACB=90°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE.
在△ACD与△BCE中,
∴△ACD≌△BCE(SAS).
(2)∵∠ACB=90°,AC=BC,∴∠A=45°.
∵△ACD≌△BCE,
∴AD=BE,∠CBE=∠A=45°.
∵AD=BF,∴BE=BF,
∴∠BEF=×(180°-45°)=67.5°.
18. 【答案】
解:(1)如图.
(2)如图.
(3)如图,∵AO=A2O==,∠AOA2=90°,∴点A所经过的路径长=×2π=π.
19. 【答案】
解:(1)①证明:如图(a),将△DBE绕点D旋转180°得到△DCG,连接FG,则△DCG≌△DBE.
∴DG=DE,CG=BE.
又∵DE⊥DF,
∴DF垂直平分线段EG,∴FG=EF.
∵在△CFG中,CG+CF>FG,
∴BE+CF>EF.
②BE2+CF2=EF2.
证明:∵∠A=90°,∴∠B+∠ACD=90°.
由①得,∠FCG=∠FCD+∠DCG=∠FCD+∠B=90°,
∴在Rt△CFG中,由勾股定理,得CG2+CF2=FG2,∴BE2+CF2=EF2.
(2)EF=BE+CF.
证明:如图(b).∵CD=BD,∠BDC=120°,
∴将△CDF绕点D逆时针旋转120°得到△BDM,
∴△BDM≌△CDF,
∴DM=DF,BM=CF,∠BDM=∠CDF,∠DBM=∠C.
∵∠ABD+∠C=180°,
∴∠ABD+∠DBM=180°,
∴点A,B,M共线,
∴∠EDM=∠EDB+∠BDM=∠EDB+∠CDF=∠BDC-∠EDF=120°-60°=60°=∠EDF.
在△DEM和△DEF中,
∴△DEM≌△DEF,
∴EF=EM=BE+BM=BE+CF.
20. 【答案】
证明:如图,将△ADB绕点D顺时针旋转60°,得到△CDE,连接BE,
则∠ADB=∠CDE,∠A=∠DCE,AB=CE,BD=DE.
又∵∠ADC=60°,∴∠BDE=60°,
∴△DBE是等边三角形,
∴BD=BE.
又∵∠ECB=360°-∠BCD-∠DCE=360°-∠BCD-∠A=360°-(360°-∠ADC-∠ABC)=90°,
∴△ECB是直角三角形,
∴BE2=CE2+BC2,即BD2=AB2+BC2.
人教版 九年级数学上册 23.2 中心对称
一、选择题
1. 下列图形中,一定既是轴对称图形又是中心对称图形的是( )
A.等边三角形 B.直角三角形
C.平行四边形 D.正方形
2. 下列四个银行标志中,既是中心对称图形,又是轴对称图形的是( )
3. 在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4. 2019·长春德惠期末 如图,△ABC与△A′B′C′关于点O中心对称,下列结论中不一定成立的是( )
A.∠ABC=∠A′C′B′ B.OA=OA′
C.BC=B′C′ D.OC=OC′
5. 如图,将△ABC以点O为旋转中心旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后变为线段E′D′.已知BC=4,则线段E′D′的长度为( )
A.2 B.3 C.4 D.1.5
6. 如图,两个半圆分别以P,O为圆心,它们成中心对称,点A1,P,B1,B2,O,A2在同一条直线上,则对称中心为( )
A.A2P的中点 B.A1B2的中点
C.A1O的中点 D.PO的中点
7. 如图示,在Rt△ABC中,∠ACB=90°.P是半圆AC的中点,连接BP交AC于点D.若半圆所在圆的圆心为O,点D,E关于圆心O对称,则图两个阴影部分的面积S1,S2之间的关系是( )
A.S1<S2 B.S1>S2 C.S1=S2 D.不确定
8. 2020·河北模拟 如图所示,A1(1,),A2(,),A3(2,),A4(3,0).作折线OA1A2A3A4关于点A4中心对称的图形,得折线A8A7A6A5A4,再作折线A8A7A6A5A4关于点A8中心对称的图形……以此类推,得到一个大的折线.现有一动点P从原点O出发,沿着折线以每秒1个单位长度的速度运动,设运动时间为t秒.当t=2020时,点P的坐标为( )
A.(1010,) B.(2020,)
C.(2016,0) D.(1010,)
二、填空题
9. 王老师、杨老师两家所在的位置关于学校对称.如果王老师家距学校2千米,那么他们两家相距________千米.
10. 若点A(x+3,2y+1)与点A′(y-5,1)关于原点对称,则点A的坐标是________.
11. 如图,已知BC为等腰三角形纸片ABC的底边,AD⊥BC,∠BAC≠90°.将此三角形纸片沿AD剪开,得到两个三角形,若把这两个三角形拼成一个四边形,则能拼出______个中心对称图形.
12. 点P(1,2)关于原点的对称点P′的坐标为__________.
13. 如图,直线a,b垂直相交于点O,曲线C是以点O为对称中心的中心对称图形,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D.若OB=3,OD=2,则阴影部分的面积为________.
14. 如图所示,在△ABC中,已知∠ACB=90°,AC=BC=2.若以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,则BB′=________.
15. 如图,将等边三角形AOB放在平面直角坐标系中,点A的坐标为(0,4),点B在第一象限,将△AOB绕点O顺时针旋转180°得到△A′OB′,则点B′的坐标是________.
16. 如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A的坐标为(a,b),则点A′的坐标为____________.
三、解答题
17. 如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
(1)试判断△BEC是不是等腰三角形,并说明理由;
(2)在原图中画△FCE,使它与△BEC关于CE的中点O中心对称,此时四边形BCFE是什么特殊平行四边形?请说明理由.
18. 如图,△ABO与△CDO关于点O中心对称,点E,F在线段AC上,且AF=CE.求证:DF=BE.
19. [材料阅读]在平面直角坐标系中,以任意两点P(x1,y1),Q(x2,y2)为端点的线段的中点坐标为.
[运用](1)已知点A(-2,1)和点B(4,-3),则线段AB的中点坐标是________;已知点M(2,3),线段MN的中点坐标是(-2,-1),则点N的坐标是________.
(2)已知平面上四点A(0,0),B(10,0),C(10,6),D(0,6).直线y=mx-3m+2将四边形ABCD分成面积相等的两部分,则m的值为________.
(3)在平面直角坐标系中,有A(-1,2),B(3,1),C(1,4)三点,另有一点D,可使以点A,B,C,D为顶点的四边形为平行四边形,求点D的坐标.
20. 如图,已知△ABC和点O.
(1)在图中画出△A′B′C′,使△A′B′C′与△ABC关于点O对称;
(2)点A,B,C,A′,B′,C′能组成哪几个平行四边形?请用符号表示出来.
人教版 九年级数学上册 23.2 中心对称 同步训练-答案
一、选择题
1. 【答案】D
2. 【答案】C
3. 【答案】D
4. 【答案】A
5. 【答案】A [解析] ∵ED是△ABC的中位线,BC=4,∴ED=2.又∵△A′B′C′和△ABC关于点O中心对称,∴E′D′=ED=2.
6. 【答案】D [解析] 因为P,O是对称点,所以PO的中点是对称中心.
7. 【答案】C [解析] ∵P是半圆AC的中点,∴半圆关于直线OP对称,且点D,E关于圆心O对称,因而S1,S2在直径AC上面的部分面积相等.∵OD=OE,∴CD=AE.∵△CDB的底边CD与△AEB的底边AE相等,高相同,∴它们的面积相等,∴S1=S2.
8. 【答案】A
二、填空题
9. 【答案】4 [解析] ∵王老师、杨老师两家所在的位置关于学校对称,
∴王老师、杨老师两家到学校的距离相等.
∵王老师家距学校2千米,
∴他们两家相距4千米.
故答案为4.
10. 【答案】(6,-1) [解析] 依题意,得解得∴点A的坐标为(6,-1).
11. 【答案】3 [解析] 在这里具有中心对称图形特征的是平行四边形,所以两个三角形中对应相等的两
条边重合只能拼一个.因为三角形只有三条边,所以只有三种情况.
12. 【答案】(-1,-2)
13. 【答案】6 [解析] 如图,过点A′作A′B′⊥a,垂足为B′,由题意可知,①与②关于点O中心对称,所以阴影部分的面积可以看作四边形A′B′OD的面积.又A′D⊥b于点D,直线a,b互相垂直,可得四边形A′B′OD是矩形,所以其面积为3×2=6.
14. 【答案】2 [解析] ∵△ABC绕AC的中点O旋转了180°,
∴OB=OB′,∴BB′=2OB.
又∵OC=OA=AC=1,BC=2,
∴在Rt△OBC中,OB===,
∴BB′=2OB=2 .
15. 【答案】(-2 ,-2) [解析] 过点B作BH⊥y轴于点H,如图.∵△OAB为等边三角形,A(0,4),∴OH=AH=2,∠BOA=60°,∴BH=OH=2 ,∴点B的坐标为(2 ,2).∵将△AOB绕点O顺时针旋转180°得到△A′OB′,∴点B′的坐标是(-2 ,-2).
16. 【答案】(-a,-b+2) [解析] 如图,过点A作AD⊥y轴于点D,过点A′作A′D′⊥y轴于点D′,则△ACD≌△A′CD′,∴A′D′=AD=a,CD′=CD=-b+1,∴OD′=-b+2,∴点A′的坐标为(-a,-b+2).
三、解答题
17. 【答案】
解:(1)△BEC是等腰三角形.
理由:∵在矩形ABCD中,AD∥BC,
∴∠DEC=∠BCE.
∵EC平分∠BED,∴∠DEC=∠BEC,
∴∠BEC=∠BCE,∴BC=BE,
∴△BEC是等腰三角形.
(2)连接BO并延长至点F,使OF=OB,连接FE,FC,△FCE即为所求.四边形BCFE是菱形.理由:
∵OB=OF,OE=OC,
∴四边形BCFE是平行四边形.
又∵BC=BE,
∴?BCFE是菱形.
18. 【答案】
证明:∵△ABO与△CDO关于点O中心对称,
∴BO=DO,AO=CO.
∵AF=CE,∴AO-AF=CO-CE,
即FO=EO.
在△FOD和△EOB中,
∴△FOD≌△EOB(SAS),
∴DF=BE.
19. 【答案】
解:(1)(1,-1) (-6,-5)
(2)
(3)设点D的坐标为(x,y).
若以AB为对角线,AC,BC为邻边的四边形为平行四边形,则AB,CD的中点重合,
∴解得
若以BC为对角线,AB,AC为邻边的四边形为平行四边形,则AD,BC的中点重合,
∴
解得
若以AC为对角线,AB,BC为邻边的四边形为平行四边形,则BD,AC的中点重合,
∴
解得
综上可知,点D的坐标为(1,-1)或(5,3)或(-3,5).
20. 【答案】
解:(1)如图所示.
(2)?ABA′B′,?BCB′C′,?CA′C′A.
23. 3 课题学习 图案设计
一、选择题(共10小题,3*10=30)
1.在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是( )
2.如图所示的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的一个是( )
3. 下面的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有( )
A.4个 B.3个
C.2个 D.1个
4. 下列基本图形中,经过平移、旋转或轴对称变换后,不能得到左图的是( )
5.把一张正方形纸片如图①,图②对折两次后,再如图③挖去一个三角形小孔,则展开后图形是( )
6.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有( )
A.1种 B.2种
C.3种 D.4种
7. 下列四个图形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是( )
8. 观察如图所摆放的五朵梅花,变换中间的一朵梅花,得到四角的梅花,下列说法错误的是( )
A.左上角梅花,只需沿对角线平移即可
B.右上角梅花,沿对角线平移后,顺时针旋转90°
C.右下角梅花,沿对角线平移后,以下底边为对称轴对称得到的
D.左下角梅花,沿对角线平移后,顺时针旋转90°
9.剪纸是中国的民间艺术,剪纸的方法很多,图中是一种剪纸方法的图示(先将纸折叠,然后再剪,展开即得到图案).下面四个图案,不能用上述方法剪出的是( )
10 一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是( )
A. B. C. D.
二.填空题(共8小题,3*8=24)
11. 下列图形均可由“基本图案”变换得到:(只填序号)
(1)平移但不能旋转的是________;
(2)可以旋转但不能平移的是________;
(3)既可以平移,也可以旋转的是________.
12.如图是古代文物上的美丽图案,你看得出这个图案是如何设计的吗?它至少需要旋转________才能与其自身重合.
13.右边的图案是由下面五种基本图形中的两种拼接而成,这两种基本图形是________.
14. 分别以正方形的各边为直径向其内部作半圆得到的图形如图所示.将该图形绕其中心旋转一个合适的角度后会与原图形重合,则这个旋转角的最小度数是____度.
15. 已知:图A、图B分别是6×6正方形网格上的两个轴对称图形(阴影部分),其面积分别为SA、SB(网格中最小的正方形面积为一个平方单位),则SA∶SB的值是_________;
16. 小军同学在网络纸上将某些图形进行平移操作,他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示,现在他将正方形ABCD从当前位置开始进行一次平移操作,平移后的正方形顶点也在格点上,则使平移前后的两个正方形组成轴对称图形的平移方向有________个.
17. 下列这些美丽的图案都是在“几何画板”软件中利用旋转的知识在一个图案的基础上加工而成的,每一个图案都可以看作是它的“基本图案”绕着它的旋转中心旋转得来的,旋转的角度正确的为__________.
18. 下列3个图形中,能通过旋转得到右侧图形的有____________.(填序号)
三.解答题(共7小题, 46分)
19.(6分) 如图,网格中每个小正方形的边长为1,请你认真观察图①中的三个网格中阴影部分构成的图案,解答下列问题:
(1)这三个图案都具有以下共同特征:都是_______对称图形,都不是___对称图形;
(2)请在图②中设计出一个面积为4,且具备上述特征的图案,要求所画图案不能与图1中给出的图案相同.
20. (6分) 实践与操作:如图①是以正方形两顶点为圆心,边长为半径,画两段相等的圆弧而成的轴对称图形,图②是以图①为基本图案经过图形变换拼成的一个中心对称图形.
(1)请你仿照图①,用两段相等的圆弧(小于或等于半圆),在图③中重新设计一个不同的轴对称图形.
(2)以你在图③中所画的图形为基本图案,经过图形变换在图④中拼成一个中心对称图形.
21. (6分) 现有如图23-3-4①所示的两种瓷砖.请从这两种瓷砖中各选2块,拼成一个新的正方形地板图案,使拼成的图案是轴对称图形或中心对称图形(如示例图②).
(要求:分别在图③、图④中设计一种与示例图不同的拼法,这两种拼法各不相同,且其中至少有一个既是轴对称图形,又是中心对称图形).
22. (6分) 在4×4的方格内选5个小正方形,让它们组成一个轴对称图形,请在图中画出你的4种方案.(每个4×4的方格内限画一种)
要求:
(1)5个小正方形必须相连(有公共边或公共顶点视为相连)
(2)将选中的小正方形方格用黑色签字笔涂成阴影图形.(若两个方案的图形经过翻折、平移、旋转后能够重合,均视为一种方案)
23.(6分) 用4块如所示的瓷砖拼成一个正方形,使所得正方形(包括色彩因素)分别是具有如下对称性的美术图案:(1)只是轴对称图形而不是中心对称图形;(2)既是轴对称图形又是中心对称图形.画出符合要求的图形各两个.
24.(8分) 为创建绿色校园,学校决定在一块正方形的空地上种植花草,现向学生征集设计图案.图案要求只能用圆弧在正方形内加以设计,使正方形和所画的圆弧构成的图案是轴对称图形.种植花草部分用阴影表示.请你在图③,图④,图⑤中画出三种不同的设计图案.提示:在两个图案中,只有半径变化而圆心不变的图案属于同一种,例如:图①,图②只能算一种.
25.(8分) 观察设计.
(1)观察如图①~④中阴影部分构成的图案,请写出这四个图案都具有的两个共同特征;
(2)借助如图⑤的网格,请设计一个新的图案,使该图案同时具有你在解答(1)中所写出的两个共同特征.(注意:新图案与图①~④的图案不能相同)
参考答案
1-5CBACC
6-10 CADCB
11. ①;②④;③
12. 120°
13. ②⑤
14. 90
15. 9∶11
16.5
17.
18. ①②③
19. 解:(1)中心,轴
(2)答案不唯一,只要符合条件即可,如图
20. 解:答案不唯一,如图
21. 解:答案不唯一,如图所示.
22. 解:如图.
23. 解:答案不惟一,例如:
24. 解:答案不唯一,如图
25. 解:(1)答案不唯一,例如,所给的四个图案具有的共同特征可以是:
①是轴对称图形;
②面积都等于四个小正方形的面积之和;
③都是直线形图案;
④图案中不含钝角等.只要写出两个即可
(2)答案不唯一,只要设计的图案同时具有所给出的两个共同特征,均正确,例如,同时具备特征①,②的部分图案如图:
一、选择题(本大题共8道小题)
1. 在平面直角坐标系中,点P(-4,2)向右平移7个单位长度得到点P1,点P1绕原点逆时针旋转90°得到点P2,则点P2的坐标是( )
A.(-2,3) B.(-3,2)
C.(2,-3) D.(3,-2)
2. 把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为 ( )
A.30° B.90° C.120° D.180°
3. 如图所示,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心是 ( )
A.点A B.点B
C.点C D.点D
4. 观察图,其中可以看成是由“基本图案”通过旋转形成的共有( )
A.1个 B.2个 C.3个 D.4个
5. 如图,将线段AB先向右平移5个单位长度,再将所得线段绕原点顺时针旋转90°,得到线段A′B′,则点B的对应点B′的坐标是( )
A.(-4,1) B.(-1,2)
C.(4,-1) D.(1,-2)
6. 如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为( )
A. B.2
C.3 D.2
7. 如图,Rt△OCB的斜边在y轴上,OC=,含30°角的顶点与原点重合,直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′,则点B的对应点B′的坐标是( )
A.(,-1) B.(1,-)
C.(2,0) D.(,0)
8. 在平面直角坐标系中,点A的坐标为(1,),以原点为中心,将点A顺时针旋转30°得到点A′,则点A′的坐标为( )
A.(,1) B.(,-1) C.(2,1) D.(0,2)
二、填空题(本大题共8道小题)
9. 如图所示,△ABC的顶点都在网格线的交点(格点)上,如果将△ABC绕点C逆时针旋转90°,那么点B的对应点B′的坐标是________.
10. 如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=________°.
11. 把二次函数y=(x-1)2+2的图象绕原点旋转180°后得到的图象的解析式为_______.
12. 在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A′B′C′,使各顶点仍在格点上,则其旋转角的度数是________.
13. 如图,两块完全相同的含30°角的三角尺ABC和A′B′C′重合在一起,将三角尺A′B′C′绕其顶点C′逆时针旋转角α(0°<α≤90°),有以下三个结论:①当α=30°时,A′C与AB的交点恰好为AB的中点;②当α=60°时,A′B′恰好经过点B;③在旋转过程中,始终存在AA′⊥BB′.其中正确结论的序号是__________.
14. 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为________.
15. 如图,在△ABC中,∠BAC=90°,AB=AC=10 cm,D为△ABC内一点,∠BAD=15°,AD=6 cm,连接BD,将△ABD绕点A逆时针旋转,使AB与AC重合,点D的对应点为点E,连接DE,DE交AC于点F,则CF的长为________ cm.
16. 如图,将Rt△ABC的斜边AB绕点A顺时针旋转α(0°<α<90°)得到AE,直角边AC绕点A逆时针旋转β(0°<β<90°)得到AF,连接EF,若AB=3,AC=2,且α+β=∠B,则EF=________.
三、解答题(本大题共4道小题)
17. 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与点A,B不重合),连接CD,将线段CD绕点C逆时针旋转90°得到线段CE,连接DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
(2)当AD=BF时,求∠BEF的度数.
18. 如图,在正方形网格中,每个小正方形的边长都是1个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,4),B(1,1),C(3,1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC绕点O逆时针旋转90°后得到的△A2B2C2;
(3)在(2)的条件下,求点A所经过的路径长(结果保留π).
19. (1)如图 (a),在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;
②若∠A=90°,探索线段BE,CF,EF之间的数量关系,并加以证明.
(2)如图(b),在四边形ABDC中,∠B+∠C=180°,BD=CD,∠BDC=120°,以D为顶点作一个60°的角,角的两边分别交AB,AC于E,F两点,连接EF,探索线段BE,CF,EF之间的数量关系,并加以证明.
20. 已知:如图,在四边形ABCD中,∠ADC=60°,∠ABC=30°,AD=CD.
求证:BD2=AB2+BC2.
人教版 九年级数学上册 23.1 图形的旋转 同步训练-答案
一、选择题(本大题共8道小题)
1. 【答案】A [解析] 点P(-4,2)向右平移7个单位长度得到点P1(3,2),点P1绕原点逆时针旋转90°得到点P2(-2,3).故选A.
2. 【答案】C
3. 【答案】B [解析] 旋转中心到对应点的距离相等.
4. 【答案】D
5. 【答案】D
6. 【答案】A [解析] ∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB=5.
∵将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,
∴AE=4,DE=3,∴BE=1.
在Rt△BED中,BD==.故选A.
7. 【答案】A
8. 【答案】A [解析] 如图,过点A作AE⊥y轴于点E,过点A′作A′F⊥x轴于点F,
∴∠AEO=∠A′FO=90°.
∵点A的坐标为(1,),∴AE=1,OE=,
∴OA=2,∠AOE=30°,由旋转可知∠AOA′=30°,OA′=OA=2,∴∠A′OF=90°-30°-30°=30°,∴A′F=OA′=1,OF=,∴A′(,1).
故选A.
二、填空题(本大题共8道小题)
9. 【答案】(1,0)
10. 【答案】20 [解析] ∵AB=AB′,∠BAB′=40°,
∴∠ABB′=70°.∵B′C′⊥AB,∴∠BB′C′=20°.
11. 【答案】y=-x2-2x-3 [解析] 旋转前二次项的系数a=1,抛物线的顶点坐标是(1,2),旋转后二次项的系数a=-1,抛物线的顶点坐标是(-1,-2),∴新抛物线的解析式为y=-(x+1)2-2,即y=-x2-2x-3.
12. 【答案】90° [解析] 找到一组对应点A,A′,并将其与旋转中心连接起来,确定旋转角,进而得到旋转角的度数为90°.
13. 【答案】①②③
14. 【答案】18 [解析] 如图.∵∠BAD=∠BCD=90°,∴∠B+∠ADC=180°.又∵AB=AD,∴将△ABC绕点A逆时针旋转90°后点B与点D重合,点C的对应点E落在CD的延长线上,∴AE=AC=6,∠CAE=90°,∴S四边形ABCD=S△ACE=AC·AE=×6×6=18.
15. 【答案】(10-2 ) [解析] 如图,过点A作AG⊥DE于点G.由旋转知,AD=AE,∠DAE=90°,∠CAE=∠BAD=15°,
∴∠AED=∠ADG=45°,
∴∠AFD=∠AED+∠CAE=60°.
在Rt△ADG中,AG=DG==3 (cm).
在Rt△AFG中,GF==(cm),AF=2FG=2 (cm),
∴CF=AC-AF=(10-2 )cm.
16. 【答案】 [解析] ∵α+β=∠B,∴∠EAF=∠BAC+∠B=90°,∴△AEF是直角三角形,且AE=AB=3,AF=AC=2,∴EF==.
三、解答题(本大题共4道小题)
17. 【答案】
解:(1)证明:由题意可知,CD=CE,∠DCE=90°.
∵∠ACB=90°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE.
在△ACD与△BCE中,
∴△ACD≌△BCE(SAS).
(2)∵∠ACB=90°,AC=BC,∴∠A=45°.
∵△ACD≌△BCE,
∴AD=BE,∠CBE=∠A=45°.
∵AD=BF,∴BE=BF,
∴∠BEF=×(180°-45°)=67.5°.
18. 【答案】
解:(1)如图.
(2)如图.
(3)如图,∵AO=A2O==,∠AOA2=90°,∴点A所经过的路径长=×2π=π.
19. 【答案】
解:(1)①证明:如图(a),将△DBE绕点D旋转180°得到△DCG,连接FG,则△DCG≌△DBE.
∴DG=DE,CG=BE.
又∵DE⊥DF,
∴DF垂直平分线段EG,∴FG=EF.
∵在△CFG中,CG+CF>FG,
∴BE+CF>EF.
②BE2+CF2=EF2.
证明:∵∠A=90°,∴∠B+∠ACD=90°.
由①得,∠FCG=∠FCD+∠DCG=∠FCD+∠B=90°,
∴在Rt△CFG中,由勾股定理,得CG2+CF2=FG2,∴BE2+CF2=EF2.
(2)EF=BE+CF.
证明:如图(b).∵CD=BD,∠BDC=120°,
∴将△CDF绕点D逆时针旋转120°得到△BDM,
∴△BDM≌△CDF,
∴DM=DF,BM=CF,∠BDM=∠CDF,∠DBM=∠C.
∵∠ABD+∠C=180°,
∴∠ABD+∠DBM=180°,
∴点A,B,M共线,
∴∠EDM=∠EDB+∠BDM=∠EDB+∠CDF=∠BDC-∠EDF=120°-60°=60°=∠EDF.
在△DEM和△DEF中,
∴△DEM≌△DEF,
∴EF=EM=BE+BM=BE+CF.
20. 【答案】
证明:如图,将△ADB绕点D顺时针旋转60°,得到△CDE,连接BE,
则∠ADB=∠CDE,∠A=∠DCE,AB=CE,BD=DE.
又∵∠ADC=60°,∴∠BDE=60°,
∴△DBE是等边三角形,
∴BD=BE.
又∵∠ECB=360°-∠BCD-∠DCE=360°-∠BCD-∠A=360°-(360°-∠ADC-∠ABC)=90°,
∴△ECB是直角三角形,
∴BE2=CE2+BC2,即BD2=AB2+BC2.
人教版 九年级数学上册 23.2 中心对称
一、选择题
1. 下列图形中,一定既是轴对称图形又是中心对称图形的是( )
A.等边三角形 B.直角三角形
C.平行四边形 D.正方形
2. 下列四个银行标志中,既是中心对称图形,又是轴对称图形的是( )
3. 在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4. 2019·长春德惠期末 如图,△ABC与△A′B′C′关于点O中心对称,下列结论中不一定成立的是( )
A.∠ABC=∠A′C′B′ B.OA=OA′
C.BC=B′C′ D.OC=OC′
5. 如图,将△ABC以点O为旋转中心旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后变为线段E′D′.已知BC=4,则线段E′D′的长度为( )
A.2 B.3 C.4 D.1.5
6. 如图,两个半圆分别以P,O为圆心,它们成中心对称,点A1,P,B1,B2,O,A2在同一条直线上,则对称中心为( )
A.A2P的中点 B.A1B2的中点
C.A1O的中点 D.PO的中点
7. 如图示,在Rt△ABC中,∠ACB=90°.P是半圆AC的中点,连接BP交AC于点D.若半圆所在圆的圆心为O,点D,E关于圆心O对称,则图两个阴影部分的面积S1,S2之间的关系是( )
A.S1<S2 B.S1>S2 C.S1=S2 D.不确定
8. 2020·河北模拟 如图所示,A1(1,),A2(,),A3(2,),A4(3,0).作折线OA1A2A3A4关于点A4中心对称的图形,得折线A8A7A6A5A4,再作折线A8A7A6A5A4关于点A8中心对称的图形……以此类推,得到一个大的折线.现有一动点P从原点O出发,沿着折线以每秒1个单位长度的速度运动,设运动时间为t秒.当t=2020时,点P的坐标为( )
A.(1010,) B.(2020,)
C.(2016,0) D.(1010,)
二、填空题
9. 王老师、杨老师两家所在的位置关于学校对称.如果王老师家距学校2千米,那么他们两家相距________千米.
10. 若点A(x+3,2y+1)与点A′(y-5,1)关于原点对称,则点A的坐标是________.
11. 如图,已知BC为等腰三角形纸片ABC的底边,AD⊥BC,∠BAC≠90°.将此三角形纸片沿AD剪开,得到两个三角形,若把这两个三角形拼成一个四边形,则能拼出______个中心对称图形.
12. 点P(1,2)关于原点的对称点P′的坐标为__________.
13. 如图,直线a,b垂直相交于点O,曲线C是以点O为对称中心的中心对称图形,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D.若OB=3,OD=2,则阴影部分的面积为________.
14. 如图所示,在△ABC中,已知∠ACB=90°,AC=BC=2.若以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,则BB′=________.
15. 如图,将等边三角形AOB放在平面直角坐标系中,点A的坐标为(0,4),点B在第一象限,将△AOB绕点O顺时针旋转180°得到△A′OB′,则点B′的坐标是________.
16. 如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A的坐标为(a,b),则点A′的坐标为____________.
三、解答题
17. 如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
(1)试判断△BEC是不是等腰三角形,并说明理由;
(2)在原图中画△FCE,使它与△BEC关于CE的中点O中心对称,此时四边形BCFE是什么特殊平行四边形?请说明理由.
18. 如图,△ABO与△CDO关于点O中心对称,点E,F在线段AC上,且AF=CE.求证:DF=BE.
19. [材料阅读]在平面直角坐标系中,以任意两点P(x1,y1),Q(x2,y2)为端点的线段的中点坐标为.
[运用](1)已知点A(-2,1)和点B(4,-3),则线段AB的中点坐标是________;已知点M(2,3),线段MN的中点坐标是(-2,-1),则点N的坐标是________.
(2)已知平面上四点A(0,0),B(10,0),C(10,6),D(0,6).直线y=mx-3m+2将四边形ABCD分成面积相等的两部分,则m的值为________.
(3)在平面直角坐标系中,有A(-1,2),B(3,1),C(1,4)三点,另有一点D,可使以点A,B,C,D为顶点的四边形为平行四边形,求点D的坐标.
20. 如图,已知△ABC和点O.
(1)在图中画出△A′B′C′,使△A′B′C′与△ABC关于点O对称;
(2)点A,B,C,A′,B′,C′能组成哪几个平行四边形?请用符号表示出来.
人教版 九年级数学上册 23.2 中心对称 同步训练-答案
一、选择题
1. 【答案】D
2. 【答案】C
3. 【答案】D
4. 【答案】A
5. 【答案】A [解析] ∵ED是△ABC的中位线,BC=4,∴ED=2.又∵△A′B′C′和△ABC关于点O中心对称,∴E′D′=ED=2.
6. 【答案】D [解析] 因为P,O是对称点,所以PO的中点是对称中心.
7. 【答案】C [解析] ∵P是半圆AC的中点,∴半圆关于直线OP对称,且点D,E关于圆心O对称,因而S1,S2在直径AC上面的部分面积相等.∵OD=OE,∴CD=AE.∵△CDB的底边CD与△AEB的底边AE相等,高相同,∴它们的面积相等,∴S1=S2.
8. 【答案】A
二、填空题
9. 【答案】4 [解析] ∵王老师、杨老师两家所在的位置关于学校对称,
∴王老师、杨老师两家到学校的距离相等.
∵王老师家距学校2千米,
∴他们两家相距4千米.
故答案为4.
10. 【答案】(6,-1) [解析] 依题意,得解得∴点A的坐标为(6,-1).
11. 【答案】3 [解析] 在这里具有中心对称图形特征的是平行四边形,所以两个三角形中对应相等的两
条边重合只能拼一个.因为三角形只有三条边,所以只有三种情况.
12. 【答案】(-1,-2)
13. 【答案】6 [解析] 如图,过点A′作A′B′⊥a,垂足为B′,由题意可知,①与②关于点O中心对称,所以阴影部分的面积可以看作四边形A′B′OD的面积.又A′D⊥b于点D,直线a,b互相垂直,可得四边形A′B′OD是矩形,所以其面积为3×2=6.
14. 【答案】2 [解析] ∵△ABC绕AC的中点O旋转了180°,
∴OB=OB′,∴BB′=2OB.
又∵OC=OA=AC=1,BC=2,
∴在Rt△OBC中,OB===,
∴BB′=2OB=2 .
15. 【答案】(-2 ,-2) [解析] 过点B作BH⊥y轴于点H,如图.∵△OAB为等边三角形,A(0,4),∴OH=AH=2,∠BOA=60°,∴BH=OH=2 ,∴点B的坐标为(2 ,2).∵将△AOB绕点O顺时针旋转180°得到△A′OB′,∴点B′的坐标是(-2 ,-2).
16. 【答案】(-a,-b+2) [解析] 如图,过点A作AD⊥y轴于点D,过点A′作A′D′⊥y轴于点D′,则△ACD≌△A′CD′,∴A′D′=AD=a,CD′=CD=-b+1,∴OD′=-b+2,∴点A′的坐标为(-a,-b+2).
三、解答题
17. 【答案】
解:(1)△BEC是等腰三角形.
理由:∵在矩形ABCD中,AD∥BC,
∴∠DEC=∠BCE.
∵EC平分∠BED,∴∠DEC=∠BEC,
∴∠BEC=∠BCE,∴BC=BE,
∴△BEC是等腰三角形.
(2)连接BO并延长至点F,使OF=OB,连接FE,FC,△FCE即为所求.四边形BCFE是菱形.理由:
∵OB=OF,OE=OC,
∴四边形BCFE是平行四边形.
又∵BC=BE,
∴?BCFE是菱形.
18. 【答案】
证明:∵△ABO与△CDO关于点O中心对称,
∴BO=DO,AO=CO.
∵AF=CE,∴AO-AF=CO-CE,
即FO=EO.
在△FOD和△EOB中,
∴△FOD≌△EOB(SAS),
∴DF=BE.
19. 【答案】
解:(1)(1,-1) (-6,-5)
(2)
(3)设点D的坐标为(x,y).
若以AB为对角线,AC,BC为邻边的四边形为平行四边形,则AB,CD的中点重合,
∴解得
若以BC为对角线,AB,AC为邻边的四边形为平行四边形,则AD,BC的中点重合,
∴
解得
若以AC为对角线,AB,BC为邻边的四边形为平行四边形,则BD,AC的中点重合,
∴
解得
综上可知,点D的坐标为(1,-1)或(5,3)或(-3,5).
20. 【答案】
解:(1)如图所示.
(2)?ABA′B′,?BCB′C′,?CA′C′A.
23. 3 课题学习 图案设计
一、选择题(共10小题,3*10=30)
1.在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是( )
2.如图所示的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的一个是( )
3. 下面的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有( )
A.4个 B.3个
C.2个 D.1个
4. 下列基本图形中,经过平移、旋转或轴对称变换后,不能得到左图的是( )
5.把一张正方形纸片如图①,图②对折两次后,再如图③挖去一个三角形小孔,则展开后图形是( )
6.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有( )
A.1种 B.2种
C.3种 D.4种
7. 下列四个图形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是( )
8. 观察如图所摆放的五朵梅花,变换中间的一朵梅花,得到四角的梅花,下列说法错误的是( )
A.左上角梅花,只需沿对角线平移即可
B.右上角梅花,沿对角线平移后,顺时针旋转90°
C.右下角梅花,沿对角线平移后,以下底边为对称轴对称得到的
D.左下角梅花,沿对角线平移后,顺时针旋转90°
9.剪纸是中国的民间艺术,剪纸的方法很多,图中是一种剪纸方法的图示(先将纸折叠,然后再剪,展开即得到图案).下面四个图案,不能用上述方法剪出的是( )
10 一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是( )
A. B. C. D.
二.填空题(共8小题,3*8=24)
11. 下列图形均可由“基本图案”变换得到:(只填序号)
(1)平移但不能旋转的是________;
(2)可以旋转但不能平移的是________;
(3)既可以平移,也可以旋转的是________.
12.如图是古代文物上的美丽图案,你看得出这个图案是如何设计的吗?它至少需要旋转________才能与其自身重合.
13.右边的图案是由下面五种基本图形中的两种拼接而成,这两种基本图形是________.
14. 分别以正方形的各边为直径向其内部作半圆得到的图形如图所示.将该图形绕其中心旋转一个合适的角度后会与原图形重合,则这个旋转角的最小度数是____度.
15. 已知:图A、图B分别是6×6正方形网格上的两个轴对称图形(阴影部分),其面积分别为SA、SB(网格中最小的正方形面积为一个平方单位),则SA∶SB的值是_________;
16. 小军同学在网络纸上将某些图形进行平移操作,他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示,现在他将正方形ABCD从当前位置开始进行一次平移操作,平移后的正方形顶点也在格点上,则使平移前后的两个正方形组成轴对称图形的平移方向有________个.
17. 下列这些美丽的图案都是在“几何画板”软件中利用旋转的知识在一个图案的基础上加工而成的,每一个图案都可以看作是它的“基本图案”绕着它的旋转中心旋转得来的,旋转的角度正确的为__________.
18. 下列3个图形中,能通过旋转得到右侧图形的有____________.(填序号)
三.解答题(共7小题, 46分)
19.(6分) 如图,网格中每个小正方形的边长为1,请你认真观察图①中的三个网格中阴影部分构成的图案,解答下列问题:
(1)这三个图案都具有以下共同特征:都是_______对称图形,都不是___对称图形;
(2)请在图②中设计出一个面积为4,且具备上述特征的图案,要求所画图案不能与图1中给出的图案相同.
20. (6分) 实践与操作:如图①是以正方形两顶点为圆心,边长为半径,画两段相等的圆弧而成的轴对称图形,图②是以图①为基本图案经过图形变换拼成的一个中心对称图形.
(1)请你仿照图①,用两段相等的圆弧(小于或等于半圆),在图③中重新设计一个不同的轴对称图形.
(2)以你在图③中所画的图形为基本图案,经过图形变换在图④中拼成一个中心对称图形.
21. (6分) 现有如图23-3-4①所示的两种瓷砖.请从这两种瓷砖中各选2块,拼成一个新的正方形地板图案,使拼成的图案是轴对称图形或中心对称图形(如示例图②).
(要求:分别在图③、图④中设计一种与示例图不同的拼法,这两种拼法各不相同,且其中至少有一个既是轴对称图形,又是中心对称图形).
22. (6分) 在4×4的方格内选5个小正方形,让它们组成一个轴对称图形,请在图中画出你的4种方案.(每个4×4的方格内限画一种)
要求:
(1)5个小正方形必须相连(有公共边或公共顶点视为相连)
(2)将选中的小正方形方格用黑色签字笔涂成阴影图形.(若两个方案的图形经过翻折、平移、旋转后能够重合,均视为一种方案)
23.(6分) 用4块如所示的瓷砖拼成一个正方形,使所得正方形(包括色彩因素)分别是具有如下对称性的美术图案:(1)只是轴对称图形而不是中心对称图形;(2)既是轴对称图形又是中心对称图形.画出符合要求的图形各两个.
24.(8分) 为创建绿色校园,学校决定在一块正方形的空地上种植花草,现向学生征集设计图案.图案要求只能用圆弧在正方形内加以设计,使正方形和所画的圆弧构成的图案是轴对称图形.种植花草部分用阴影表示.请你在图③,图④,图⑤中画出三种不同的设计图案.提示:在两个图案中,只有半径变化而圆心不变的图案属于同一种,例如:图①,图②只能算一种.
25.(8分) 观察设计.
(1)观察如图①~④中阴影部分构成的图案,请写出这四个图案都具有的两个共同特征;
(2)借助如图⑤的网格,请设计一个新的图案,使该图案同时具有你在解答(1)中所写出的两个共同特征.(注意:新图案与图①~④的图案不能相同)
参考答案
1-5CBACC
6-10 CADCB
11. ①;②④;③
12. 120°
13. ②⑤
14. 90
15. 9∶11
16.5
17.
18. ①②③
19. 解:(1)中心,轴
(2)答案不唯一,只要符合条件即可,如图
20. 解:答案不唯一,如图
21. 解:答案不唯一,如图所示.
22. 解:如图.
23. 解:答案不惟一,例如:
24. 解:答案不唯一,如图
25. 解:(1)答案不唯一,例如,所给的四个图案具有的共同特征可以是:
①是轴对称图形;
②面积都等于四个小正方形的面积之和;
③都是直线形图案;
④图案中不含钝角等.只要写出两个即可
(2)答案不唯一,只要设计的图案同时具有所给出的两个共同特征,均正确,例如,同时具备特征①,②的部分图案如图:
同课章节目录
