17.1 第1课时 勾股定理 课件(共44张PPT)
文档属性
| 名称 | 17.1 第1课时 勾股定理 课件(共44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 19:50:21 | ||
图片预览







文档简介
(共44张PPT)
第十七章
勾股定理
17.1
勾股定理
第1课时
勾股定理
人教版
八年级数学下册
教学课件
1.
新课目标
1
2.
情景导学
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
新课目标
新课目标
【学习目标】
1.经历探索及验证勾股定理的过程,体会数形结合的思想.
2.掌握勾股定理,并运用它解决简单的计算题;
3.了解利用拼图验证勾股定理的方法,培养在实际生活中发现问题总结规律的意识和能力.
【学习重点】
探索和验证勾股定理.
【学习难点】
在方格纸上通过计算面积的方法探索勾股定理、勾股定理的证明.
第二部分
情景导学
问题1:如图所示的图形像一棵枝叶茂盛、姿态优美的树,这就是著名的毕达哥拉斯树,它由若干个图形组成,而每个图形的基本元素是三个正方形和一个直角三角形.各组图形大小不一,但形状一致,结构奇巧.你能说说其中的奥秘吗?
情景导学
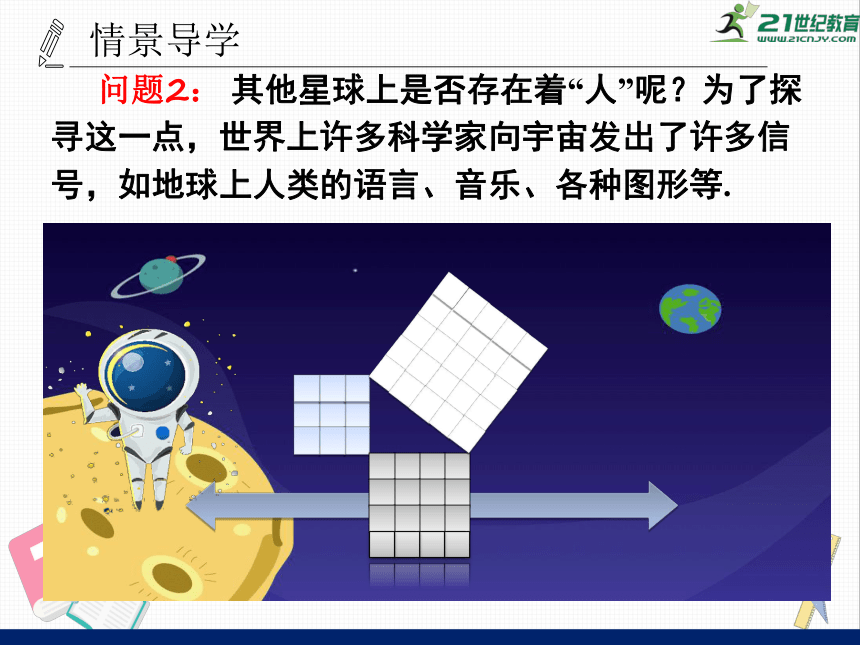
问题2:
其他星球上是否存在着“人”呢?为了探寻这一点,世界上许多科学家向宇宙发出了许多信号,如地球上人类的语言、音乐、各种图形等.
情景导学
据说我国著名的数学家华罗庚曾建议“发射”一种勾股定理的图形(如图).
很多学者认为如果宇宙“人”也拥有文明的话,那么他们一定会认识这种语言,因为几乎所有具有古代文化的民族和国家都对勾股定理有所了解.
第三部分
新课进行时
新课进行时
核心知识点一
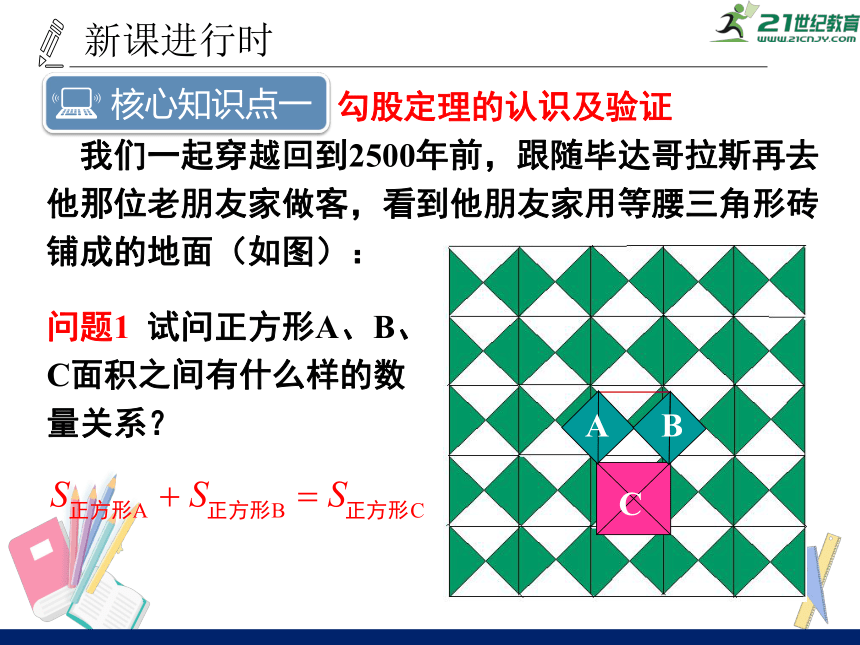
我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用等腰三角形砖铺成的地面(如图):
A
B
C
问题1
试问正方形A、B、C面积之间有什么样的数量关系?
勾股定理的认识及验证
新课进行时
A
B
C
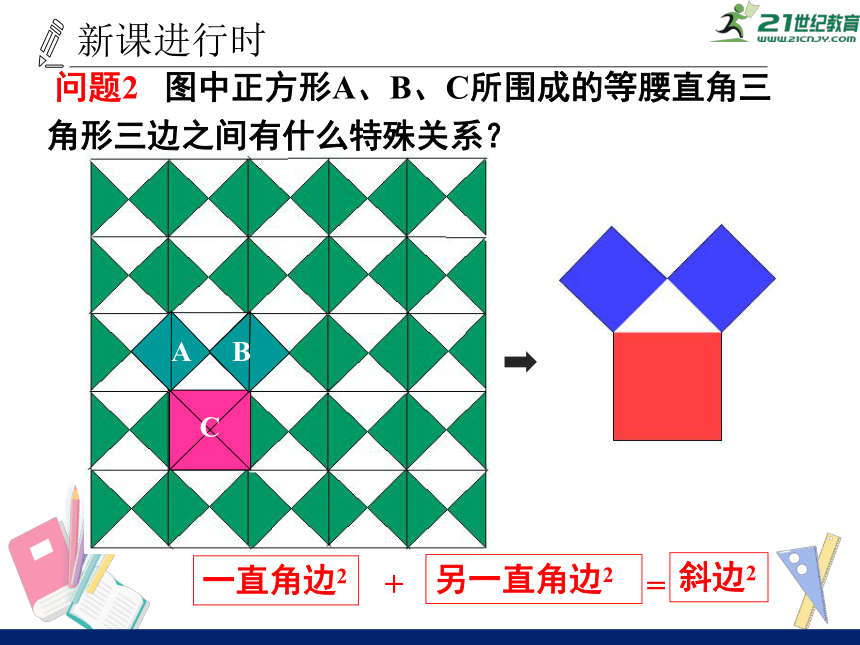
一直角边2
另一直角边2
斜边2
+
=
问题2
图中正方形A、B、C所围成的等腰直角三角形三边之间有什么特殊关系?
新课进行时
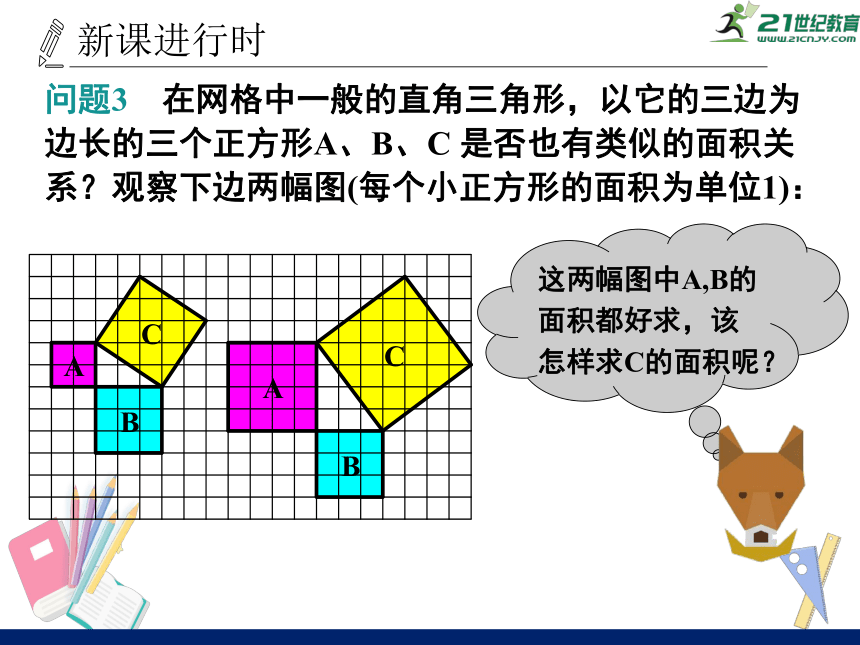
问题3 在网格中一般的直角三角形,以它的三边为边长的三个正方形A、B、C
是否也有类似的面积关系?观察下边两幅图(每个小正方形的面积为单位1):
这两幅图中A,B的面积都好求,该怎样求C的面积呢?
新课进行时
方法1:补形法(把以斜边为边长的正方形补成各边都在网格线上的正方形):
左图:
右图:
新课进行时
方法2:分割法(把以斜边为边长的正方形分割成易求出面积的三角形和四边形):
左图:
右图:
你还有其他办法求C的面积吗?
新课进行时
根据前面求出的C的面积直接填出下表:
A的面积
B的面积
C的面积
左图
右图
4
13
25
9
16
9
思考
正方形A、B、C
所围成的直角三角形三条边之间有怎样的特殊关系?
新课进行时
命题1
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
由上面的几个例子,我们猜想:
a
b
c
下面动图形象的说明命题1的正确性,让我们跟着以前的数学家们用拼图法来证明这一猜想.
新课进行时
a
b
b
c
a
b
c
证法1
让我们跟着我国汉代数学家赵爽拼图,再用所拼的图形证明命题吧.
a
新课进行时
a
b
c
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
赵爽弦图
b-a
证明:
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因为,这个图案被选为2002年在北京召开的国际数学大会的会徽.
新课进行时
证法2
毕达哥拉斯证法,请先用手中的四个全等的直角三角形按图示进行拼图,然后分析其面积关系后证明吧.
新课进行时
a
a
a
a
b
b
b
b
c
c
c
c
∴a2+b2+2ab=c2+2ab,
∴a2
+b2
=c2.
证明:
∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+
S小正方形
=4×
ab+c2
=c2+2ab,
新课进行时
a
a
b
b
c
c
∴a2
+
b2
=
c2.
证法3
美国第二十任总统伽菲尔德的“总统证法”.
如图,图中的三个三角形都是直角三角形,求证:a2
+
b2
=
c2.
新课进行时
在我国又称商高定理,在外国则叫毕达哥拉斯定理,或百牛定理.
a、b、c为正数
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
公式变形:
勾股定理
a
b
c
新课进行时
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
勾2+股2=弦2
新课进行时
例1
如图,在Rt△ABC中,
∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
解:
(1)据勾股定理得
(2)据勾股定理得
C
A
B
利用勾股定理进行计算
核心知识点二
新课进行时
(1)若a:b=1:2
,c=5,求a;
(2)若b=15,∠A=30°,求a,c.
【变式题1】在Rt△ABC中,
∠C=90°.
解:
(1)设a=x,b=2x,根据勾股定理建立方程得
x2+(2x)2=52,
解得
(2)
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152,
解得
已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
归纳
新课进行时
【变式题2】
在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图?,
当BC为斜边时,如图?,
4
3
A
C
B
4
3
C
A
B
图?
图?
当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易丢解.
归纳
新课进行时
例2
已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解:由勾股定理可得
AB2=AC2+BC2=25,
即
AB=5.
根据三角形面积公式,
∴
AC×BC=
AB×CD.
∴
CD=
.
A
D
B
C
3
4
由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,它常与勾股定理联合使用.
归纳
新课进行时
求下列图中未知数x、y的值:
解:由勾股定理可得
81+
144=x2,
解得x=15.
解:由勾股定理可得
y2+
144=169,
解得
y=5
新课进行时
一判断题.
1.?ABC的两边AB=5,AC=12,则BC=13
(
)
2.?
ABC的a=6,b=8,则c=10
(
)
二填空题
1.在?
ABC中,
∠C=90°,AC=6,CB=8,则
?ABC面积为_____,斜边为上的高为______.
?
?
24
4.8
A
B
C
D
第四部分
知识小结
知识小结
勾股定理
内容
在Rt△ABC中,
∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
第五部分
随堂演练
随堂演练
1.下列说法中,正确的是
(
)
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
2.图中阴影部分是一个正方形,则此正方形的面积为
.
8
cm
10
cm
36
cm?
随堂演练
3、在波平如静的湖面上,有一朵美丽的红莲
,它高出水面1米
,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米
,问这里水深多少?
x+1
B
C
A
H
1
2
?
┓
x
x2+22=(x+1)2
随堂演练
3
.观察下列表格:
……
列举
猜想
3、4、5
32=4+5
5、12、13
52=12+13
7、24、25
72=24+25
……
13、b、c
132=b+c
84
85
请你结合该表格及相关知识,求出b、c的值.
即b=
,c=
随堂演练
4.在△ABC中,∠C=90°.
(1)若a=15,b=8,则c=
.
(2)若c=13,b=12,则a=
.
4.若直角三角形中,有两边长是5和7,则第三边长
的平方为_________.
17
5
74或24
随堂演练
5.求斜边长17
cm、一条直角边长15
cm的直角三角形的面积.
解:设另一条直角边长是x
cm.
由勾股定理得152+
x2
=172,
即x2=172-152=289–225=64,
∴
x=±8(负值舍去),
∴另一直角边长为8
cm,
直角三角形的面积是
(cm2).
随堂演练
6.如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1,求△ABC的周长.
解:∵AD⊥BC,∴∠ADB=∠ADC=90°.
在Rt△ADB中,∵∠B+∠BAD=90°,∠B=45°,
∴∠B=∠BAD=45°,
∴BD=AD=1,∴AB=
.
在Rt△ADC中,∵∠C=30°,
∴AC=2AD=2,
∴CD=
,∴BC=BD+CD=1+
,
∴△ABC的周长=AB+AC+BC=
.
随堂演练
2.如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了
(
)
A.7m
B.8m
C.9m
D.10m
8m
A
B
C
2m
随堂演练
解:∵AE=BE,
∴S△ABE=
AE·BE=
AE2.
又∵AE2+BE2=AB2,
∴2AE2=AB2,
∴S△ABE=
AB2=
;
同理可得S△AHC+S△BCF=
AC2+
BC2.
又∵AC2+BC2=AB2,
∴阴影部分的面积为
AB2=
.
7.如图,以Rt△ABC的三边长为斜边分别向外作等腰直角三角形.若斜边AB=3,求△ABE及阴影部分的面积.
第六部分
课后作业
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
第十七章
勾股定理
17.1
勾股定理
第1课时
勾股定理
人教版
八年级数学下册
教学课件
1.
新课目标
1
2.
情景导学
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
新课目标
新课目标
【学习目标】
1.经历探索及验证勾股定理的过程,体会数形结合的思想.
2.掌握勾股定理,并运用它解决简单的计算题;
3.了解利用拼图验证勾股定理的方法,培养在实际生活中发现问题总结规律的意识和能力.
【学习重点】
探索和验证勾股定理.
【学习难点】
在方格纸上通过计算面积的方法探索勾股定理、勾股定理的证明.
第二部分
情景导学
问题1:如图所示的图形像一棵枝叶茂盛、姿态优美的树,这就是著名的毕达哥拉斯树,它由若干个图形组成,而每个图形的基本元素是三个正方形和一个直角三角形.各组图形大小不一,但形状一致,结构奇巧.你能说说其中的奥秘吗?
情景导学
问题2:
其他星球上是否存在着“人”呢?为了探寻这一点,世界上许多科学家向宇宙发出了许多信号,如地球上人类的语言、音乐、各种图形等.
情景导学
据说我国著名的数学家华罗庚曾建议“发射”一种勾股定理的图形(如图).
很多学者认为如果宇宙“人”也拥有文明的话,那么他们一定会认识这种语言,因为几乎所有具有古代文化的民族和国家都对勾股定理有所了解.
第三部分
新课进行时
新课进行时
核心知识点一
我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用等腰三角形砖铺成的地面(如图):
A
B
C
问题1
试问正方形A、B、C面积之间有什么样的数量关系?
勾股定理的认识及验证
新课进行时
A
B
C
一直角边2
另一直角边2
斜边2
+
=
问题2
图中正方形A、B、C所围成的等腰直角三角形三边之间有什么特殊关系?
新课进行时
问题3 在网格中一般的直角三角形,以它的三边为边长的三个正方形A、B、C
是否也有类似的面积关系?观察下边两幅图(每个小正方形的面积为单位1):
这两幅图中A,B的面积都好求,该怎样求C的面积呢?
新课进行时
方法1:补形法(把以斜边为边长的正方形补成各边都在网格线上的正方形):
左图:
右图:
新课进行时
方法2:分割法(把以斜边为边长的正方形分割成易求出面积的三角形和四边形):
左图:
右图:
你还有其他办法求C的面积吗?
新课进行时
根据前面求出的C的面积直接填出下表:
A的面积
B的面积
C的面积
左图
右图
4
13
25
9
16
9
思考
正方形A、B、C
所围成的直角三角形三条边之间有怎样的特殊关系?
新课进行时
命题1
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
由上面的几个例子,我们猜想:
a
b
c
下面动图形象的说明命题1的正确性,让我们跟着以前的数学家们用拼图法来证明这一猜想.
新课进行时
a
b
b
c
a
b
c
证法1
让我们跟着我国汉代数学家赵爽拼图,再用所拼的图形证明命题吧.
a
新课进行时
a
b
c
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
赵爽弦图
b-a
证明:
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因为,这个图案被选为2002年在北京召开的国际数学大会的会徽.
新课进行时
证法2
毕达哥拉斯证法,请先用手中的四个全等的直角三角形按图示进行拼图,然后分析其面积关系后证明吧.
新课进行时
a
a
a
a
b
b
b
b
c
c
c
c
∴a2+b2+2ab=c2+2ab,
∴a2
+b2
=c2.
证明:
∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+
S小正方形
=4×
ab+c2
=c2+2ab,
新课进行时
a
a
b
b
c
c
∴a2
+
b2
=
c2.
证法3
美国第二十任总统伽菲尔德的“总统证法”.
如图,图中的三个三角形都是直角三角形,求证:a2
+
b2
=
c2.
新课进行时
在我国又称商高定理,在外国则叫毕达哥拉斯定理,或百牛定理.
a、b、c为正数
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
公式变形:
勾股定理
a
b
c
新课进行时
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
勾2+股2=弦2
新课进行时
例1
如图,在Rt△ABC中,
∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
解:
(1)据勾股定理得
(2)据勾股定理得
C
A
B
利用勾股定理进行计算
核心知识点二
新课进行时
(1)若a:b=1:2
,c=5,求a;
(2)若b=15,∠A=30°,求a,c.
【变式题1】在Rt△ABC中,
∠C=90°.
解:
(1)设a=x,b=2x,根据勾股定理建立方程得
x2+(2x)2=52,
解得
(2)
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152,
解得
已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
归纳
新课进行时
【变式题2】
在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图?,
当BC为斜边时,如图?,
4
3
A
C
B
4
3
C
A
B
图?
图?
当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易丢解.
归纳
新课进行时
例2
已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解:由勾股定理可得
AB2=AC2+BC2=25,
即
AB=5.
根据三角形面积公式,
∴
AC×BC=
AB×CD.
∴
CD=
.
A
D
B
C
3
4
由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,它常与勾股定理联合使用.
归纳
新课进行时
求下列图中未知数x、y的值:
解:由勾股定理可得
81+
144=x2,
解得x=15.
解:由勾股定理可得
y2+
144=169,
解得
y=5
新课进行时
一判断题.
1.?ABC的两边AB=5,AC=12,则BC=13
(
)
2.?
ABC的a=6,b=8,则c=10
(
)
二填空题
1.在?
ABC中,
∠C=90°,AC=6,CB=8,则
?ABC面积为_____,斜边为上的高为______.
?
?
24
4.8
A
B
C
D
第四部分
知识小结
知识小结
勾股定理
内容
在Rt△ABC中,
∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
第五部分
随堂演练
随堂演练
1.下列说法中,正确的是
(
)
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
2.图中阴影部分是一个正方形,则此正方形的面积为
.
8
cm
10
cm
36
cm?
随堂演练
3、在波平如静的湖面上,有一朵美丽的红莲
,它高出水面1米
,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米
,问这里水深多少?
x+1
B
C
A
H
1
2
?
┓
x
x2+22=(x+1)2
随堂演练
3
.观察下列表格:
……
列举
猜想
3、4、5
32=4+5
5、12、13
52=12+13
7、24、25
72=24+25
……
13、b、c
132=b+c
84
85
请你结合该表格及相关知识,求出b、c的值.
即b=
,c=
随堂演练
4.在△ABC中,∠C=90°.
(1)若a=15,b=8,则c=
.
(2)若c=13,b=12,则a=
.
4.若直角三角形中,有两边长是5和7,则第三边长
的平方为_________.
17
5
74或24
随堂演练
5.求斜边长17
cm、一条直角边长15
cm的直角三角形的面积.
解:设另一条直角边长是x
cm.
由勾股定理得152+
x2
=172,
即x2=172-152=289–225=64,
∴
x=±8(负值舍去),
∴另一直角边长为8
cm,
直角三角形的面积是
(cm2).
随堂演练
6.如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1,求△ABC的周长.
解:∵AD⊥BC,∴∠ADB=∠ADC=90°.
在Rt△ADB中,∵∠B+∠BAD=90°,∠B=45°,
∴∠B=∠BAD=45°,
∴BD=AD=1,∴AB=
.
在Rt△ADC中,∵∠C=30°,
∴AC=2AD=2,
∴CD=
,∴BC=BD+CD=1+
,
∴△ABC的周长=AB+AC+BC=
.
随堂演练
2.如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了
(
)
A.7m
B.8m
C.9m
D.10m
8m
A
B
C
2m
随堂演练
解:∵AE=BE,
∴S△ABE=
AE·BE=
AE2.
又∵AE2+BE2=AB2,
∴2AE2=AB2,
∴S△ABE=
AB2=
;
同理可得S△AHC+S△BCF=
AC2+
BC2.
又∵AC2+BC2=AB2,
∴阴影部分的面积为
AB2=
.
7.如图,以Rt△ABC的三边长为斜边分别向外作等腰直角三角形.若斜边AB=3,求△ABE及阴影部分的面积.
第六部分
课后作业
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
