4.4图形变化的简单应用 同步练习(含答案)
文档属性
| 名称 | 4.4图形变化的简单应用 同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第四章 图形的平移与旋转
4 图形变化的简单应用
考点突破
考点 图形变化的简单应用
例 如图是小亮运用图形变化设计地板砖图案的形成过程,由图(1)是如何得到图(2)的?由图(2)是如何得到图(3)的?
思路导引: 有关图案设计问题,首先要确定基本图形,再利用轴对称、平移、旋转及中心对称等图形的变换进行设计.这类问题一般为开放性试题,答案不唯一。
方法归纳
1.我们可以利用平移、轴对称和旋转中的一种进行图案设计,还可以利用它们的组合进行图案设计。
2.图案设计的三个步骤:
(1)选择基本图案。
(2)制定设计思路。
(3)利用图形变换或图形变换组合作图。
题组训练
1.下面四个图案中,能由基本图形通过旋转而得到的是( )
2.如图所示的紫荆花图案,可以看作是由一个基本图形绕点O连续旋转得到的,该旋转角度是( )
72? B. 108°
C. 144° D. 216°
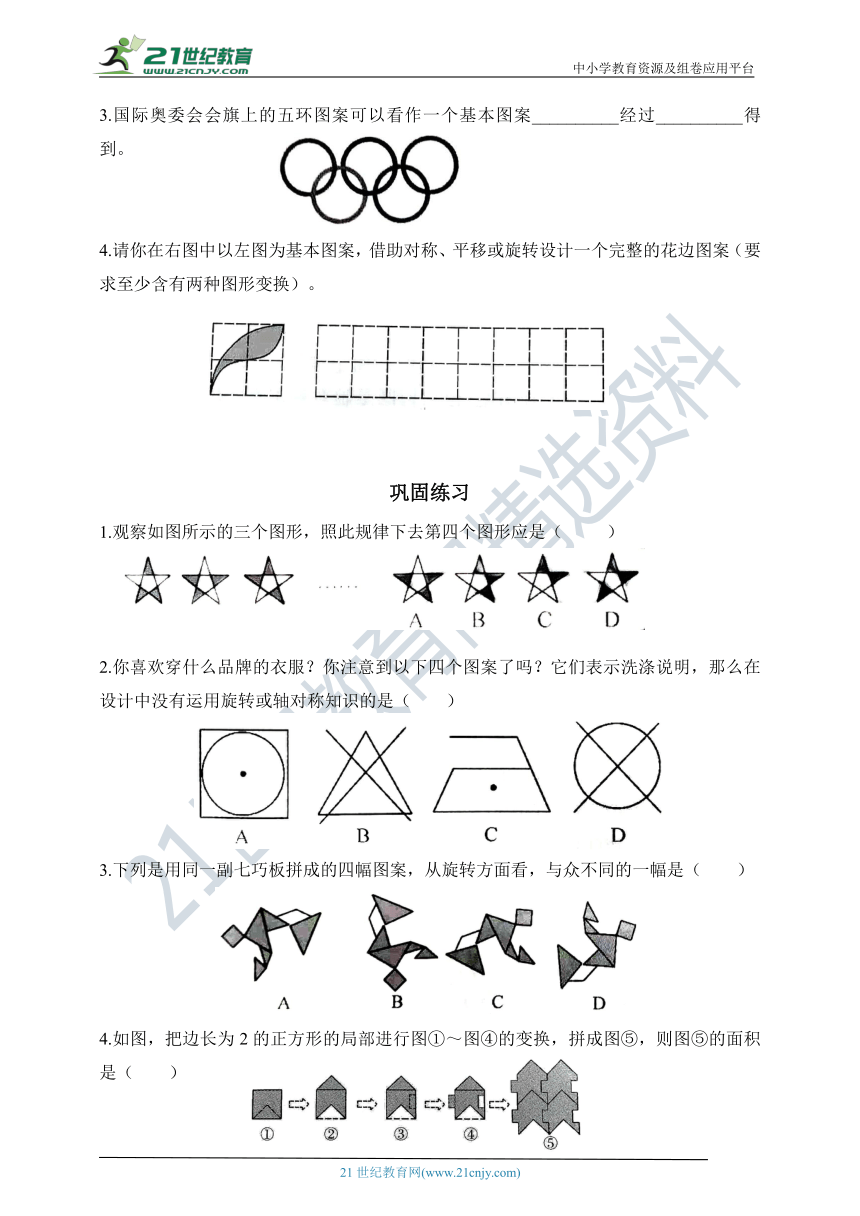
3.国际奥委会会旗上的五环图案可以看作一个基本图案__________经过__________得到。
4.请你在右图中以左图为基本图案,借助对称、平移或旋转设计一个完整的花边图案(要求至少含有两种图形变换)。
巩固练习
1.观察如图所示的三个图形,照此规律下去第四个图形应是( )
2.你喜欢穿什么品牌的衣服?你注意到以下四个图案了吗?它们表示洗涤说明,那么在设计中没有运用旋转或轴对称知识的是( )
3.下列是用同一副七巧板拼成的四幅图案,从旋转方面看,与众不同的一幅是( )
4.如图,把边长为2的正方形的局部进行图①~图④的变换,拼成图⑤,则图⑤的面积是( )
12 B. 14 C. 16 D. 18
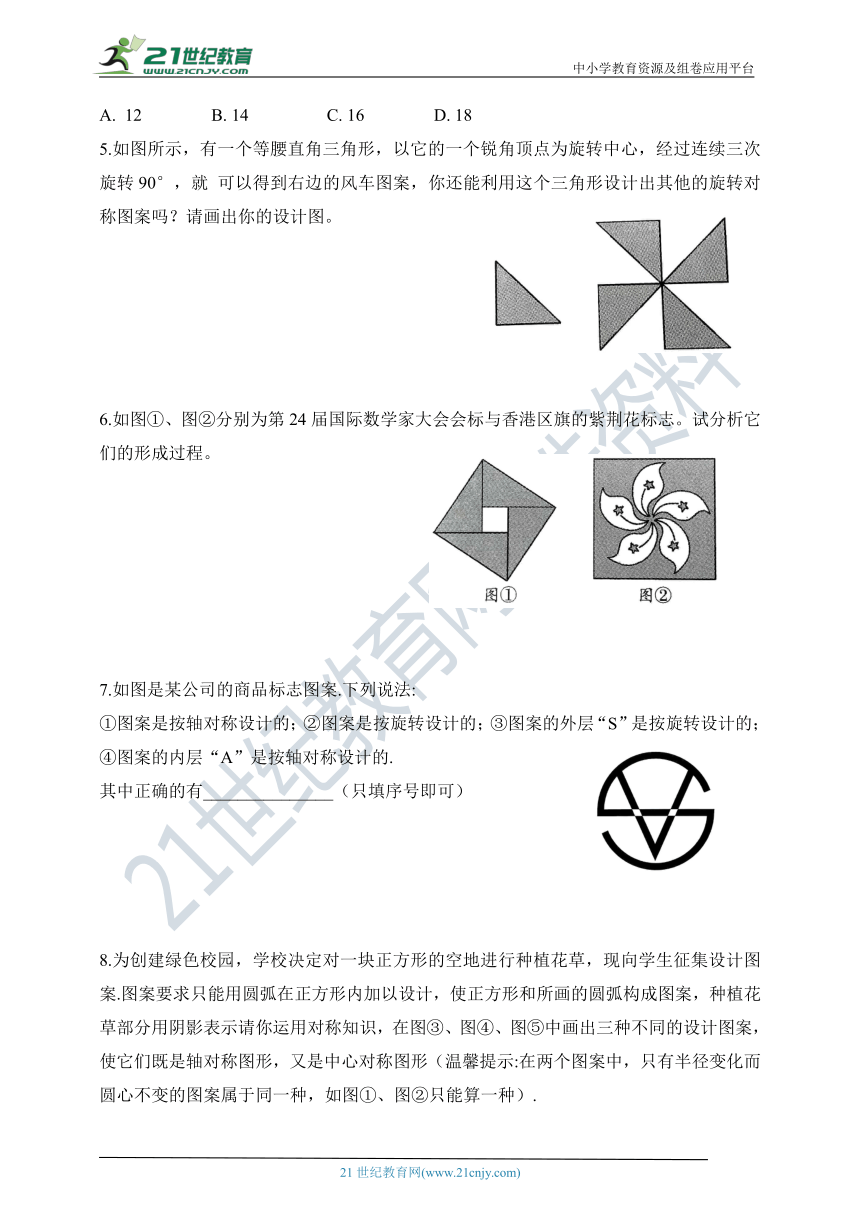
5.如图所示,有一个等腰直角三角形,以它的一个锐角顶点为旋转中心,经过连续三次旋转90°,就 可以得到右边的风车图案,你还能利用这个三角形设计出其他的旋转对称图案吗?请画出你的设计图。
6.如图①、图②分别为第24届国际数学家大会会标与香港区旗的紫荆花标志。试分析它们的形成过程。
7.如图是某公司的商品标志图案.下列说法:
①图案是按轴对称设计的;②图案是按旋转设计的;③图案的外层“S”是按旋转设计的;④图案的内层“A”是按轴对称设计的.
其中正确的有_______________(只填序号即可)
8.为创建绿色校园,学校决定对一块正方形的空地进行种植花草,现向学生征集设计图案.图案要求只能用圆弧在正方形内加以设计,使正方形和所画的圆弧构成图案,种植花草部分用阴影表示请你运用对称知识,在图③、图④、图⑤中画出三种不同的设计图案,使它们既是轴对称图形,又是中心对称图形(温馨提示:在两个图案中,只有半径变化而圆心不变的图案属于同一种,如图①、图②只能算一种).
9.把一个简单图形通过平移可以得到简洁而美丽的镶边图案,如下图所示.请你也利用平移知识构思并画出你喜欢的镶边图案.
10.你能用平移分析图中的图案是如何形成的吗?它是由哪个“基本图案”经过多次平移得到的?请画出这个“基本图形”.
11.实践与操作:如图①是以正方形两顶点为圆心,边长为半径,画两段相等的圆弧而成的轴对称图形,图②是以图①为基本图案,经过图形变换拼成的一个中心对称图形.
(1)请你仿照图①,用两段相等的圆弧(大于或等于半圆),在图③中重新设计一个不同的轴对称图形;
(2)请你以在图③中所画的图形为基本图案,经过图形变换在图④中拼成一个中心对称图形.
参考答案
考点突破
例 解:答案不唯一,如可由图(1)通过轴对称或中心对称或旋转得到图(2),再由图(2)通过轴对称或旋转得到图(3)。
题组训练
D 2. A
3. 圆环 四次平移
4. 解:答案不唯一,以下提供三种图案。
巩固练习
D 2. C 3. C 4. C
解:如下图供参考。
解:第24届国际数学家大会会标,可以看作是以其中一个直角三角形为基本图案,绕图形的中心按同一方向连续旋转3次,且每次旋转90?形成的;香港区旗的紫荆花标志,可以看作是以其中一个花瓣为基本图案,绕图形的中心按同一方向连续旋转4次,且每次旋转72?形成的。
③④
解:如下各图供参考。
解:如下各图供参考。
解:基本图形是
解:答案不唯一,如
如图。
如图。
_21?????????è?????(www.21cnjy.com)_
第四章 图形的平移与旋转
4 图形变化的简单应用
考点突破
考点 图形变化的简单应用
例 如图是小亮运用图形变化设计地板砖图案的形成过程,由图(1)是如何得到图(2)的?由图(2)是如何得到图(3)的?
思路导引: 有关图案设计问题,首先要确定基本图形,再利用轴对称、平移、旋转及中心对称等图形的变换进行设计.这类问题一般为开放性试题,答案不唯一。
方法归纳
1.我们可以利用平移、轴对称和旋转中的一种进行图案设计,还可以利用它们的组合进行图案设计。
2.图案设计的三个步骤:
(1)选择基本图案。
(2)制定设计思路。
(3)利用图形变换或图形变换组合作图。
题组训练
1.下面四个图案中,能由基本图形通过旋转而得到的是( )
2.如图所示的紫荆花图案,可以看作是由一个基本图形绕点O连续旋转得到的,该旋转角度是( )
72? B. 108°
C. 144° D. 216°
3.国际奥委会会旗上的五环图案可以看作一个基本图案__________经过__________得到。
4.请你在右图中以左图为基本图案,借助对称、平移或旋转设计一个完整的花边图案(要求至少含有两种图形变换)。
巩固练习
1.观察如图所示的三个图形,照此规律下去第四个图形应是( )
2.你喜欢穿什么品牌的衣服?你注意到以下四个图案了吗?它们表示洗涤说明,那么在设计中没有运用旋转或轴对称知识的是( )
3.下列是用同一副七巧板拼成的四幅图案,从旋转方面看,与众不同的一幅是( )
4.如图,把边长为2的正方形的局部进行图①~图④的变换,拼成图⑤,则图⑤的面积是( )
12 B. 14 C. 16 D. 18
5.如图所示,有一个等腰直角三角形,以它的一个锐角顶点为旋转中心,经过连续三次旋转90°,就 可以得到右边的风车图案,你还能利用这个三角形设计出其他的旋转对称图案吗?请画出你的设计图。
6.如图①、图②分别为第24届国际数学家大会会标与香港区旗的紫荆花标志。试分析它们的形成过程。
7.如图是某公司的商品标志图案.下列说法:
①图案是按轴对称设计的;②图案是按旋转设计的;③图案的外层“S”是按旋转设计的;④图案的内层“A”是按轴对称设计的.
其中正确的有_______________(只填序号即可)
8.为创建绿色校园,学校决定对一块正方形的空地进行种植花草,现向学生征集设计图案.图案要求只能用圆弧在正方形内加以设计,使正方形和所画的圆弧构成图案,种植花草部分用阴影表示请你运用对称知识,在图③、图④、图⑤中画出三种不同的设计图案,使它们既是轴对称图形,又是中心对称图形(温馨提示:在两个图案中,只有半径变化而圆心不变的图案属于同一种,如图①、图②只能算一种).
9.把一个简单图形通过平移可以得到简洁而美丽的镶边图案,如下图所示.请你也利用平移知识构思并画出你喜欢的镶边图案.
10.你能用平移分析图中的图案是如何形成的吗?它是由哪个“基本图案”经过多次平移得到的?请画出这个“基本图形”.
11.实践与操作:如图①是以正方形两顶点为圆心,边长为半径,画两段相等的圆弧而成的轴对称图形,图②是以图①为基本图案,经过图形变换拼成的一个中心对称图形.
(1)请你仿照图①,用两段相等的圆弧(大于或等于半圆),在图③中重新设计一个不同的轴对称图形;
(2)请你以在图③中所画的图形为基本图案,经过图形变换在图④中拼成一个中心对称图形.
参考答案
考点突破
例 解:答案不唯一,如可由图(1)通过轴对称或中心对称或旋转得到图(2),再由图(2)通过轴对称或旋转得到图(3)。
题组训练
D 2. A
3. 圆环 四次平移
4. 解:答案不唯一,以下提供三种图案。
巩固练习
D 2. C 3. C 4. C
解:如下图供参考。
解:第24届国际数学家大会会标,可以看作是以其中一个直角三角形为基本图案,绕图形的中心按同一方向连续旋转3次,且每次旋转90?形成的;香港区旗的紫荆花标志,可以看作是以其中一个花瓣为基本图案,绕图形的中心按同一方向连续旋转4次,且每次旋转72?形成的。
③④
解:如下各图供参考。
解:如下各图供参考。
解:基本图形是
解:答案不唯一,如
如图。
如图。
_21?????????è?????(www.21cnjy.com)_
