五年级数学下册课件-9.2 图形与几何-人教版(共31张PPT)
文档属性
| 名称 | 五年级数学下册课件-9.2 图形与几何-人教版(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 09:39:13 | ||
图片预览



文档简介
(共31张PPT)
2
图形与几何
总复习
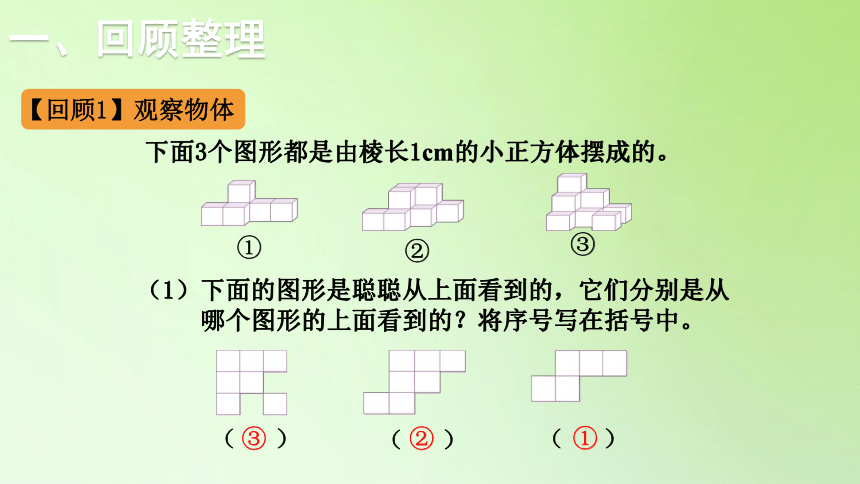
下面3个图形都是由棱长1cm的小正方体摆成的。
①
②
③
(1)下面的图形是聪聪从上面看到的,它们分别是从
哪个图形的上面看到的?将序号写在括号中。
(
)
(
)
(
)
③
②
①
一、回顾整理
【回顾1】观察物体
(
)
(
)
(
)
(2)①、②、③的体积分别是多少?①的体积是③
的体积的几分之几?
①的体积是6立方厘米,②的体积是10立方厘米,③的体积是11立方厘米。
①的体积是③的体积的
。
一、回顾整理
【回顾1】观察物体
下面3个图形都是由棱长1cm的小正方体摆成的。
①
②
③
1.认识旋转。
(1)物体绕着某一点或某条轴转动的现象,叫做旋转。
(2)图形旋转前后,形状和大小都没有发生变化,只是
位置发生了变化。
2.旋转作图的方法。
(1)找出图形的关键点或线段;
(2)画出关键点或线段旋转后的位置;
(3)顺次连接所画出旋转后的对应点。
【回顾2】图形与几何
一、回顾整理
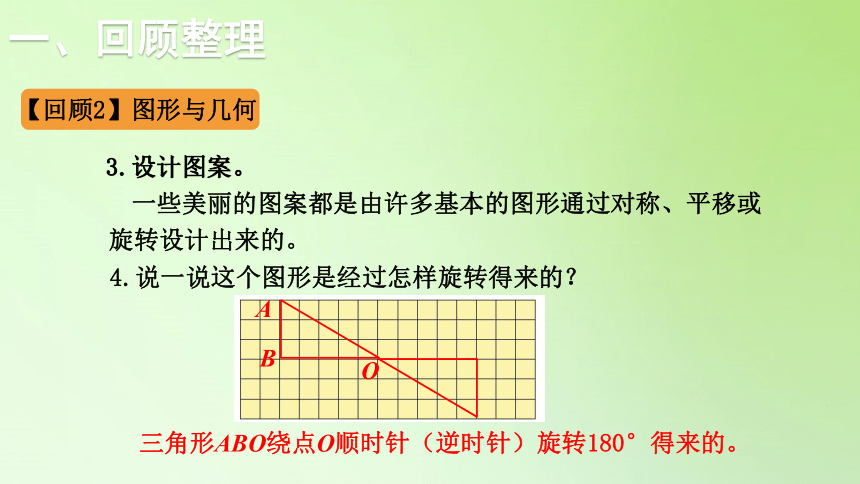
3.设计图案。
【回顾2】图形与几何
一、回顾整理
一些美丽的图案都是由许多基本的图形通过对称、平移或旋转设计出来的。
4.说一说这个图形是经过怎样旋转得来的?
三角形ABO绕点O顺时针(逆时针)旋转180°得来的。
O
A
B
一、回顾整理
【回顾3】长方体和正方体
1.长方体的特征。
长方体有6个面,长方体的这6个面一般都是长方形,特殊情况会有两个相对的面是正方形,相对的两个面完全相同。
2.长方体有多少条棱?哪些棱长度相等?长方体有几个顶点?
长方体有12条棱,相对的棱长度相等,相交于同一顶点的三
条棱的长度分别叫做长方体的长、宽、高;有8个顶点。
一、回顾整理
【回顾3】长方体和正方体
3.正方体的特征。
正方体有6个面,6个面完全相同,都是正方形。正方体有12条棱,12条棱长度都相等。
长方体
正方体
相同点
6个面、12条棱、8个顶点
不同点
6个面都是长方形(有时相对的两个面是正方形),相对面完全相同
6个面都是正方形,
6个面完全相同
相对棱的长度相等
12条棱长度都相等
正方体是特殊的长方体,用集合图表示:
长方体
正方体
一、回顾整理
【回顾3】长方体和正方体
4.长方体和正方体的相同点和不同点。
(1)长方体表面积的含义
30
10
8
后
前
上
下
左
右
●
30
10
8
单位:厘米
长方体6个面的总面积,就是长方体的表面积。
一、回顾整理
【回顾3】长方体和正方体
5.长方体和正方体的表面积。
前
后
上
下
左
右
正方形展开图的每个面都是正方形,边长就是正方形的棱长,每个面的面积都等于棱长乘棱长。
一、回顾整理
【回顾3】长方体和正方体
5.长方体和正方体的表面积。
(2)正方体表面积的含义
第一类:中间四连方,两侧各有一个,共6种
图(1)
图(2)
图(3)
图(6)
图(5)
图(4)
一、回顾整理
【回顾3】长方体和正方体
5.长方体和正方体的表面积。
(3)正方形的11种展开图。
图(8)
图(9)
图(7)
一、回顾整理
【回顾3】长方体和正方体
(3)正方形的11种展开图。
5.长方体和正方体的表面积。
第二类:中间三连方,一侧有一个、一侧有二个,共3种
第三类:中间两连方,两侧各有2个、只有1种
第四类:两排各有3个、只有1种
图(10)
图(11)
一、回顾整理
5.长方体和正方体的表面积。
(3)正方形的11种展开图。
【回顾3】长方体和正方体
底面积
长方体(或正方体)
的体积
=
底面积×高
长方体的体积
=
长×宽×高
底面积
正方体的体积
=
棱长×棱长×棱长
可看作是高
一、回顾整理
【回顾3】长方体和正方体
6.长方体、正方体体积公式的推导。
名
称
图形及条件
表
面
积
体
积
长方体
长方形的表面积=(长×宽+长×高+宽×高)
用字母表示为:
S=
长方形的体积=长×宽×高
用字母表示为:
V=
正方体
正方形的表面积=棱长×棱长×6
用字母表示为:
S=
正方形的体积=棱长×棱长×棱长
用字母表示为:
V=
a
b
h
a
a
a
2(ab+ah+bh)
abh
3
a
6a
2
一、回顾整理
【回顾3】长方体和正方体
一、回顾整理
【回顾3】长方体和正方体
7.容积。
(1)容器所能容纳物体的体积,通常叫做它的容积。
(2)计量容积一般就用体积单位。计量液体的体积,常用
容积单位升和毫升。
(3)容积单位升(L)和毫升(mL)间的关系:1L
=
1000mL;
容积单位和体积单位的关系:1L=1
,1mL=1
.
3
cm
3
dm
体积
容积
区别
意义不同
物体所占空间的大小,叫做物体的体积。
一个容器所能容纳物体的体积,叫做这个容器的容积。
测量方法不同
从物体外部测量长、宽、高。
从容器里面测量长、宽、高。
单位名称不同
m?、dm?、cm?。
容积单位:L和mL;计量固体时用体积单位。
联系
1.容积的大小是通过所能容纳物体的体积表示出来的。
2.计算方法相同。
一、回顾整理
【回顾3】长方体和正方体
7.容积。
(4)体积与容积的区别与联系
一、回顾整理
【回顾3】长方体和正方体
8.看图解答问题。
6dm
4dm
5dm
(1)如图,这个长方体的表面积是多少?
S=2(ab+ah+bh)
=2×(6×5+6×4+5×4)
=148(
)
答:这个长方体的表面积是148
。
2
dm
2
dm
一、回顾整理
【回顾3】长方体和正方体
8.看图解答问题。
6dm
4dm
5dm
(2)如果这个长方体箱子没有盖子,那么要扣除哪个面的面积?需要材料的面积是多少?
S=148-ab
=118(
)
答:要扣除上面那个面的面积,需要材料的面积118
。
2
dm
2
dm
一、回顾整理
【回顾3】长方体和正方体
8.看图解答问题。
6dm
4dm
5dm
(3)如果要在这个箱子的四周贴上一圈包装纸,包装纸的面积是多少?扣除哪些面的面积?
S=148-2ab
=88(
)
答:扣除上、下两个面的面积,包装纸的面积是88
。
2
dm
2
dm
一、回顾整理
【回顾3】长方体和正方体
8.看图解答问题。
6dm
4dm
5dm
(4)这个箱子的容积是多少?
V=abh
=6×5×4
=120(
) 120(
)=0.12(L)
答:这个箱子的容积是0.12L。
3
dm
3
dm
二、知识应用
1.总复习第3(1)题。
(1)说一说左图可以通过怎样的变换得到右图?
二、知识应用
记左图中的图形最右边的顶点为O。绕点O,将图形顺时针依次旋转90°,180°,270°可得到右图。
二、知识应用
2.一个长方体粮仓,里面长20m、宽12m。如果存放的稻谷高3.5m,1L稻谷的质量是0.78kg。这个粮仓存放的稻谷有多少吨?
这道题是先求容积,再求质量的问题。解题时应注意什么?
求容积先求体积,再换算成容积,最后求质量。
V=abh
=20×12×3.5
=840(
)
840
=840000
=840000L
0.78×840000÷1000=655.2(吨)
答:这个粮仓存放的稻谷有655.2吨。
3
m
3
m
3
dm
名
称
图形及条件
表
面
积
体
积
长方体
S=
V=
正方体
S=
V=
a
b
h
a
a
a
2(ab+ah+bh)
abh
3
a
6a
2
三、巩固反馈
11.填写下表。
三、巩固反馈
12.(1)举例说明1cm?、1dm?、1m?各有多大,1L、1mL的水大约
有多少。
1cm?:一个手指尖;1dm?:一个粉笔盒;1m?:一个洗衣机。1L大约有2瓶矿泉水那么多,1mL大约有20滴水那么多。
(2)1cm?=
dm?
700dm?=
m?
81dm?=
mL
1L=
dm?
2.3dm?=
cm?
560mL=
L
1000
0.7
81
1
2300
0.56
三、巩固反馈
13.一块长方形铁皮(如右图),从四个角
各切掉一个边长为5cm的正方形,然后做成盒子。这个盒子用了多少铁皮?它的容积有多少?
25cm
30cm
30×25-5×5×4=650(cm
)
(30-5×2)×(25-5×2)×5=1500(cm?)
1500cm?=1500mL
答:这个盒子用了650cm
铁皮,它的容积有1500mL。
三、巩固反馈
14.一个长方体的玻璃缸,长8dm,宽6dm,
高4dm,水深2.8dm。如果投入一块棱
长为4
dm的正方体铁块(如右图),
缸里的水溢出多少升?
4
-8×6×(4-2.8)=6.4(dm?)
6.4dm?=6.4L
答:缸里的水溢出6.4L。
三、巩固反馈
15.用4个
摆一摆。
(1)如果从左侧看到的形状是
,这4个小正方体可能是
怎样摆放的?
答案不唯一。可能是如下方式摆放:
三、巩固反馈
15.用4个
摆一摆。
(2)请你再给出从另一个方向看到的形状,让同桌猜一猜4
个
是怎样摆放的。
答案不唯一。例如:从上面看为
,则(1)中的图形①满足条件。
四、课堂小结
2
图形与几何
总复习
下面3个图形都是由棱长1cm的小正方体摆成的。
①
②
③
(1)下面的图形是聪聪从上面看到的,它们分别是从
哪个图形的上面看到的?将序号写在括号中。
(
)
(
)
(
)
③
②
①
一、回顾整理
【回顾1】观察物体
(
)
(
)
(
)
(2)①、②、③的体积分别是多少?①的体积是③
的体积的几分之几?
①的体积是6立方厘米,②的体积是10立方厘米,③的体积是11立方厘米。
①的体积是③的体积的
。
一、回顾整理
【回顾1】观察物体
下面3个图形都是由棱长1cm的小正方体摆成的。
①
②
③
1.认识旋转。
(1)物体绕着某一点或某条轴转动的现象,叫做旋转。
(2)图形旋转前后,形状和大小都没有发生变化,只是
位置发生了变化。
2.旋转作图的方法。
(1)找出图形的关键点或线段;
(2)画出关键点或线段旋转后的位置;
(3)顺次连接所画出旋转后的对应点。
【回顾2】图形与几何
一、回顾整理
3.设计图案。
【回顾2】图形与几何
一、回顾整理
一些美丽的图案都是由许多基本的图形通过对称、平移或旋转设计出来的。
4.说一说这个图形是经过怎样旋转得来的?
三角形ABO绕点O顺时针(逆时针)旋转180°得来的。
O
A
B
一、回顾整理
【回顾3】长方体和正方体
1.长方体的特征。
长方体有6个面,长方体的这6个面一般都是长方形,特殊情况会有两个相对的面是正方形,相对的两个面完全相同。
2.长方体有多少条棱?哪些棱长度相等?长方体有几个顶点?
长方体有12条棱,相对的棱长度相等,相交于同一顶点的三
条棱的长度分别叫做长方体的长、宽、高;有8个顶点。
一、回顾整理
【回顾3】长方体和正方体
3.正方体的特征。
正方体有6个面,6个面完全相同,都是正方形。正方体有12条棱,12条棱长度都相等。
长方体
正方体
相同点
6个面、12条棱、8个顶点
不同点
6个面都是长方形(有时相对的两个面是正方形),相对面完全相同
6个面都是正方形,
6个面完全相同
相对棱的长度相等
12条棱长度都相等
正方体是特殊的长方体,用集合图表示:
长方体
正方体
一、回顾整理
【回顾3】长方体和正方体
4.长方体和正方体的相同点和不同点。
(1)长方体表面积的含义
30
10
8
后
前
上
下
左
右
●
30
10
8
单位:厘米
长方体6个面的总面积,就是长方体的表面积。
一、回顾整理
【回顾3】长方体和正方体
5.长方体和正方体的表面积。
前
后
上
下
左
右
正方形展开图的每个面都是正方形,边长就是正方形的棱长,每个面的面积都等于棱长乘棱长。
一、回顾整理
【回顾3】长方体和正方体
5.长方体和正方体的表面积。
(2)正方体表面积的含义
第一类:中间四连方,两侧各有一个,共6种
图(1)
图(2)
图(3)
图(6)
图(5)
图(4)
一、回顾整理
【回顾3】长方体和正方体
5.长方体和正方体的表面积。
(3)正方形的11种展开图。
图(8)
图(9)
图(7)
一、回顾整理
【回顾3】长方体和正方体
(3)正方形的11种展开图。
5.长方体和正方体的表面积。
第二类:中间三连方,一侧有一个、一侧有二个,共3种
第三类:中间两连方,两侧各有2个、只有1种
第四类:两排各有3个、只有1种
图(10)
图(11)
一、回顾整理
5.长方体和正方体的表面积。
(3)正方形的11种展开图。
【回顾3】长方体和正方体
底面积
长方体(或正方体)
的体积
=
底面积×高
长方体的体积
=
长×宽×高
底面积
正方体的体积
=
棱长×棱长×棱长
可看作是高
一、回顾整理
【回顾3】长方体和正方体
6.长方体、正方体体积公式的推导。
名
称
图形及条件
表
面
积
体
积
长方体
长方形的表面积=(长×宽+长×高+宽×高)
用字母表示为:
S=
长方形的体积=长×宽×高
用字母表示为:
V=
正方体
正方形的表面积=棱长×棱长×6
用字母表示为:
S=
正方形的体积=棱长×棱长×棱长
用字母表示为:
V=
a
b
h
a
a
a
2(ab+ah+bh)
abh
3
a
6a
2
一、回顾整理
【回顾3】长方体和正方体
一、回顾整理
【回顾3】长方体和正方体
7.容积。
(1)容器所能容纳物体的体积,通常叫做它的容积。
(2)计量容积一般就用体积单位。计量液体的体积,常用
容积单位升和毫升。
(3)容积单位升(L)和毫升(mL)间的关系:1L
=
1000mL;
容积单位和体积单位的关系:1L=1
,1mL=1
.
3
cm
3
dm
体积
容积
区别
意义不同
物体所占空间的大小,叫做物体的体积。
一个容器所能容纳物体的体积,叫做这个容器的容积。
测量方法不同
从物体外部测量长、宽、高。
从容器里面测量长、宽、高。
单位名称不同
m?、dm?、cm?。
容积单位:L和mL;计量固体时用体积单位。
联系
1.容积的大小是通过所能容纳物体的体积表示出来的。
2.计算方法相同。
一、回顾整理
【回顾3】长方体和正方体
7.容积。
(4)体积与容积的区别与联系
一、回顾整理
【回顾3】长方体和正方体
8.看图解答问题。
6dm
4dm
5dm
(1)如图,这个长方体的表面积是多少?
S=2(ab+ah+bh)
=2×(6×5+6×4+5×4)
=148(
)
答:这个长方体的表面积是148
。
2
dm
2
dm
一、回顾整理
【回顾3】长方体和正方体
8.看图解答问题。
6dm
4dm
5dm
(2)如果这个长方体箱子没有盖子,那么要扣除哪个面的面积?需要材料的面积是多少?
S=148-ab
=118(
)
答:要扣除上面那个面的面积,需要材料的面积118
。
2
dm
2
dm
一、回顾整理
【回顾3】长方体和正方体
8.看图解答问题。
6dm
4dm
5dm
(3)如果要在这个箱子的四周贴上一圈包装纸,包装纸的面积是多少?扣除哪些面的面积?
S=148-2ab
=88(
)
答:扣除上、下两个面的面积,包装纸的面积是88
。
2
dm
2
dm
一、回顾整理
【回顾3】长方体和正方体
8.看图解答问题。
6dm
4dm
5dm
(4)这个箱子的容积是多少?
V=abh
=6×5×4
=120(
) 120(
)=0.12(L)
答:这个箱子的容积是0.12L。
3
dm
3
dm
二、知识应用
1.总复习第3(1)题。
(1)说一说左图可以通过怎样的变换得到右图?
二、知识应用
记左图中的图形最右边的顶点为O。绕点O,将图形顺时针依次旋转90°,180°,270°可得到右图。
二、知识应用
2.一个长方体粮仓,里面长20m、宽12m。如果存放的稻谷高3.5m,1L稻谷的质量是0.78kg。这个粮仓存放的稻谷有多少吨?
这道题是先求容积,再求质量的问题。解题时应注意什么?
求容积先求体积,再换算成容积,最后求质量。
V=abh
=20×12×3.5
=840(
)
840
=840000
=840000L
0.78×840000÷1000=655.2(吨)
答:这个粮仓存放的稻谷有655.2吨。
3
m
3
m
3
dm
名
称
图形及条件
表
面
积
体
积
长方体
S=
V=
正方体
S=
V=
a
b
h
a
a
a
2(ab+ah+bh)
abh
3
a
6a
2
三、巩固反馈
11.填写下表。
三、巩固反馈
12.(1)举例说明1cm?、1dm?、1m?各有多大,1L、1mL的水大约
有多少。
1cm?:一个手指尖;1dm?:一个粉笔盒;1m?:一个洗衣机。1L大约有2瓶矿泉水那么多,1mL大约有20滴水那么多。
(2)1cm?=
dm?
700dm?=
m?
81dm?=
mL
1L=
dm?
2.3dm?=
cm?
560mL=
L
1000
0.7
81
1
2300
0.56
三、巩固反馈
13.一块长方形铁皮(如右图),从四个角
各切掉一个边长为5cm的正方形,然后做成盒子。这个盒子用了多少铁皮?它的容积有多少?
25cm
30cm
30×25-5×5×4=650(cm
)
(30-5×2)×(25-5×2)×5=1500(cm?)
1500cm?=1500mL
答:这个盒子用了650cm
铁皮,它的容积有1500mL。
三、巩固反馈
14.一个长方体的玻璃缸,长8dm,宽6dm,
高4dm,水深2.8dm。如果投入一块棱
长为4
dm的正方体铁块(如右图),
缸里的水溢出多少升?
4
-8×6×(4-2.8)=6.4(dm?)
6.4dm?=6.4L
答:缸里的水溢出6.4L。
三、巩固反馈
15.用4个
摆一摆。
(1)如果从左侧看到的形状是
,这4个小正方体可能是
怎样摆放的?
答案不唯一。可能是如下方式摆放:
三、巩固反馈
15.用4个
摆一摆。
(2)请你再给出从另一个方向看到的形状,让同桌猜一猜4
个
是怎样摆放的。
答案不唯一。例如:从上面看为
,则(1)中的图形①满足条件。
四、课堂小结
