人教版八年级数学上册14.3因式分解---十字相乘法课件(29张)
文档属性
| 名称 | 人教版八年级数学上册14.3因式分解---十字相乘法课件(29张) |

|
|
| 格式 | zip | ||
| 文件大小 | 781.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 00:00:00 | ||
图片预览




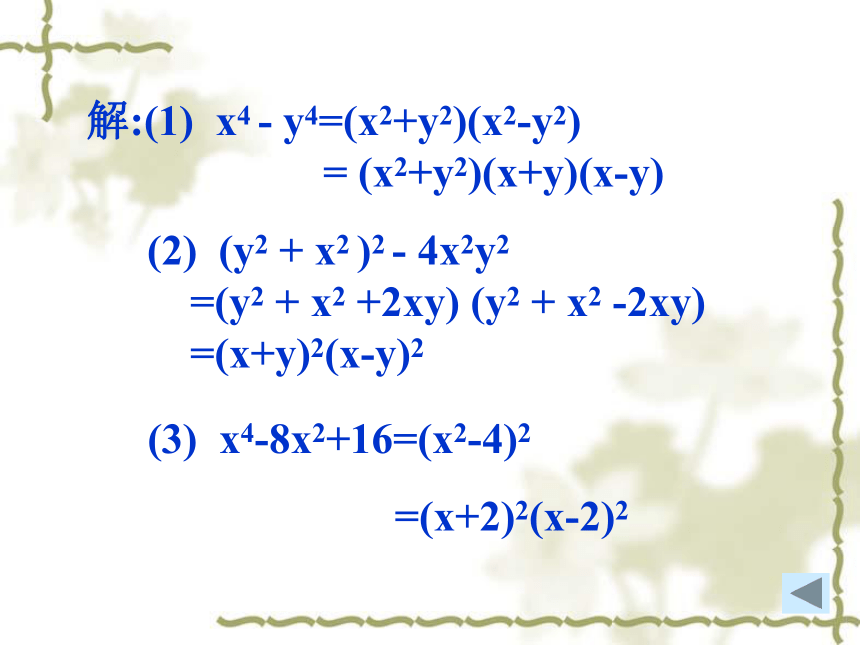
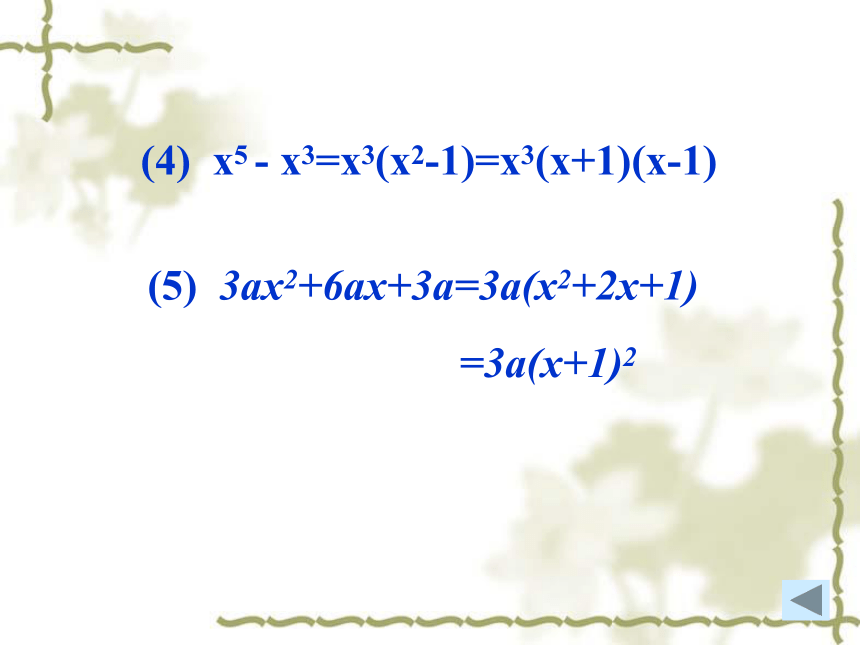


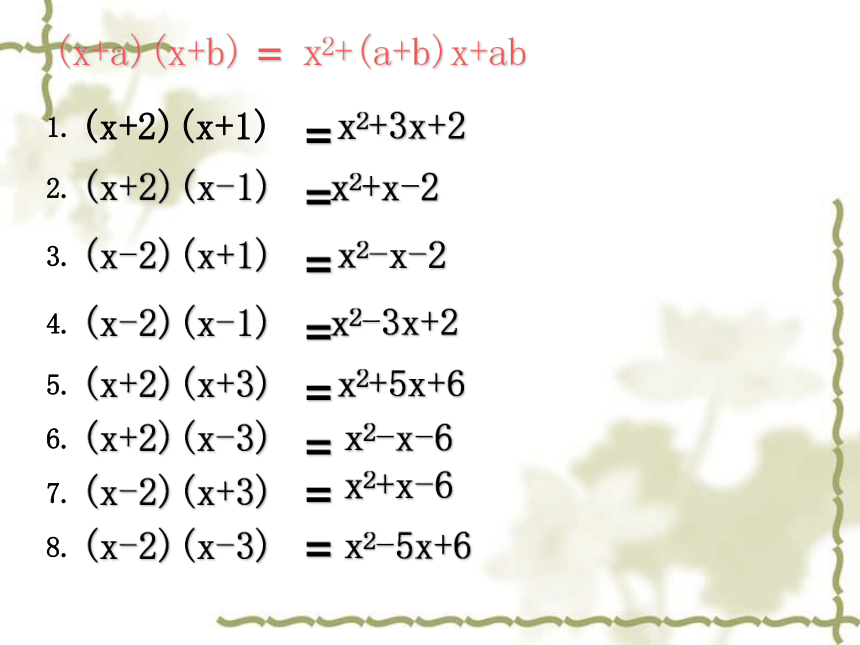
文档简介
(共29张PPT)
人教版八年级数学上册
14.3
因式分解
14.3.3
十字相乘法
探索并运用十字相乘法进行因式分解;
会综合运用学过的方法对多项式进行因式分解。
学习目标
知识回顾
1.举例说明因式分解与整式乘法的关系
2.我们已经学习了哪些因式分解的方法?
提公因式法:
ma+mb+mc=m(a+b+c)
运用公式法:
a2-b2=(a+b)(a-b)
a2
±2ab+b2=(a
±b)2
(5)
3ax2+6ax+3a
(4)
x5
-
x3
(1)
x4
-
y4
(2)
(y2
+
x2
)2
-
4x2y2
(6)
2ax2+6ax+4a
(3)
x4-8x2+16
3.把下列各式因式分解:
解:(1)
x4
-
y4=(x2+y2)(x2-y2)
=
(x2+y2)(x+y)(x-y)
(2)
(y2
+
x2
)2
-
4x2y2
=(y2
+
x2
+2xy)
(y2
+
x2
-2xy)
=(x+y)2(x-y)2
(3)
x4-8x2+16=(x2-4)2
=(x+2)2(x-2)2
(4)
x5
-
x3=x3(x2-1)=x3(x+1)(x-1)
(5)
3ax2+6ax+3a=3a(x2+2x+1)
=3a(x+1)2
(6)
2ax2+6ax+4a=2a(x2+3x+2)
你认为这个多项式因式还能分解吗?
=2a(x+1)(x+2)
十字相乘法分解因式
1.(x+2)(x+1)=
x2+3x+2
3.(x-2)(x+1)=
x2-x-2
4.(x-2)(x-1)=
x2-3x+2
2.(x+2)(x-1)=
x2+x-2
5.(x+2)(x+3)=
x2+5x+6
6.(x+2)(x-3)=
x2-x-6
7.(x-2)(x+3)=
x2+x-6
8.(x-2)(x-3)=
x2-5x+6
(x+a)(x+b)
=x2+(a+b)x+ab
请直接口答计算结果:
(x+2)(x+1)
x2+3x+2
(x-2)(x+1)
x2-x-2
(x-2)(x-1)
x2-3x+2
(x+2)(x-1)
x2+x-2
(x+2)(x+3)
x2+5x+6
(x+2)(x-3)
x2-x-6
(x-2)(x+3)
x2+x-6
(x-2)(x-3)
x2-5x+6
(x+a)(x+b)
=
x2+(a+b)x+ab
=
=
=
=
=
=
=
=
1.
2.
3.
4.
5.
6.
7.
8.
(x+a)(x+b)=x2+(a+b)x+ab
观察与发现
两个一次二项式相乘的积
一个二次三项式
整式的乘法
反过来,得
x2+(a+b)x+ab=(x+a)(x+b)
一个二次三项式
两个一次二项式相乘的积
因式分解
如果二次三项式x2+px+q中的常数项系数q能分解成两个因数a、b的积,即q=ab而且一次项系数p又恰好是a、b的和,即p=a+b,那么x2+px+q就可以进行如上的因式分解。
分析∵
(+1)
×(+2)=+2
(+1)+(+2)=+3
∴
试一试:把x2+3x+2分解因式
常数项
一次项系数
十字交叉线
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法。
十字相乘法公式:
请大家记住公式
例1:
分解因式:
x2+4x+3=_______
x2-2x-3=________
(x+3)(x+1)
(x-3)(x+1)
x
x
x
x
3
1
-3
1
例2:试将
分解因式
提示:当二次项系数为-1时
,先提出负号再因式分解
。
16
6
2
+
-
-
x
x
独立练习:把下列各式分解因式
?
课堂小结
对二次三项式x2+px+q用x2+(a+b)x+ab=(x+a)(x+b)进行因式分解,应重点掌握以下问题:
2.掌握方法:拆分常数项,验证一次项.
3.符号规律:
当q>0时,a、b同号,且a、b的符号与p的符号相同;
当q<0时,a、b异号,且绝对值较大的因数与p的符号相同.
1.适用范围:只有当q=ab,且p=a+b时
才能用十字相乘法进
我
行分解。
十字相乘法分解因式(2)
本节课解决两个问题:
第一:对形如ax2+bx+c
(a≠0)的二次三项式
进行因式分解;
第二:对形如ax2+bxy+cy2
(a≠0)的二次三项式
进行因式分解;
a2
c1
c2
a1c2+a2c1=b
a1
(a1x+c1)
(a2x+c2)
=ax2+bx+c
(a≠0)
ax2+bx+c=(a1x+c1)
(a2x+c2)
(a≠0)
整式运算
因式分解
a2
c1
c2
a1c2+a2c1=b
a1
(a1x+c1y)
(a2x+c2y)
=ax2+bxy+cy2
ax2+bxy+cy2=(a1x+c1y)
(a2x+c2y)
整式运算
因式分解
例1:2x2-7x+3
总结:
1、由常数项的符号确定分解的两数的符号
2、由一次项系数确定分解的方向
3、勿忘检验分解的合理性
1
-1
-3
2
×
(-3)+(-1)
×
1=-7
2
解:原式=(2x-1)(x-3)
=
17
3
x2
+
11
x
+
10
6
x2
+
7
x
+
2
2
3
1
2
4
+
3
=
7
∴6x2+7x+2=(2x+1)(3x+2)
1
3
5
2
2
+
15
=
11
1
3
2
5
5
+
6
∴3x2+11x+10=(x+2)(3x+5)
=
–6
5
x2
–
6
xy
–
8
y2
试因式分解5x2–6xy–8y2。
这里仍然可以用十字相乘法。
1
5
–2
4
4
–
10
∴5x2–6xy–8y2
=(x–2y)(5x+4y)
简记口诀:
首尾分解,交叉相乘,求和凑中。
十字相乘法②随堂练习:
1)4a2–9a+2
2)7a2–19a–6
3)2(x2+y2)+5xy
例
.将
2(6x2
+x)
2-11(6x2
+x)
+5
分解因式
解:2(6x2
+x)2-11(6x2
+x)
+5
=
[(6x2
+x)
-5][2(6x2
+x)-1]
=
(6x2
+x-5)
(12x2
+2x-1
)
=
(6x
-5)(x
+1)
(12x2
+2x-1
)
1
2
-5
-1
-1-10=-11
6
1
-5
1
-5+6=1
练习:将下列各式分解因式
1、
7x
-13x+6
2
3、
15x
+7xy-4y
2
2
2、
-y
-4y+12
2
答案(7x-6)(x-1)
4、
x
-(a+1)
x+a
2
答案-
(y+6)(y-2)
答案
(3x-y)(5x+4y)
答案
(x-1)(x-a)
分组分解法
要发现式中隐含的条件,通过交换项的位置,添、去括号等一些变换达到因式分解的目的。
例1:因式分解
ab–ac+bd–cd
。
解:原式
=
(ab
–
ac)
+
(bd
–
cd)
=
a
(b
–
c)
+
d
(b
–
c)
=
(a
+
d)
(b
–
c)
还有别的解法吗?
分组分解法
要发现式中隐含的条件,通过交换项的位置,添、去括号等一些变换达到因式分解的目的。
例1:因式分解
ab–ac+bd–cd
。
解:原式
=
(ab
+
bd)
–
(ac
+
cd)
=
b
(a
+
d)
–
c
(a
+
d)
=
(a
+
d)
(b
–
c)
回顾例题:因式分解
x5+x4+x3+x2+x+1
。
另解:原式
=
(x5+x4)+(x3+x2)+(x+1)
=
(x+1)(x4+x2+1)
=
(x+1)(x4+2x2+1–x2)
=
(x+1)[(x2+1)2–x2]
=
(x+1)(x2+x+1)(x2–x+1)
拆项添项法
怎么结果与刚才不一样呢?
因为它还可以继续因式分解
例
因式分解
x4
+
4
解:原式
=
x4
+
4x2
+
4
–
4x2
=
(x2+2)2
–
(2x)2
=
(x2+2x+2)(x2–2x+2)
都是平方项
猜测使用完全平方公式
完全平方公式
平方差公式
拆项添项法随堂练习:
1)x4–23x2y2+y4
2)(m2–1)(n2–1)+4mn
配方法
配方法是一种特殊的拆项添项法,将多项式配成完全平方式,再用平方差公式进行分解。
因式分解
a2–b2+4a+2b+3
。
解:原式
=
(a2+4a+4)
–
(b2–2b+1)
=
(a+2)2
–
(b–1)2
=
(a+b+1)(a–b+3)
配方法
(拆项添项法)分组分解法
完全平方公式
平方差公式
人教版八年级数学上册
14.3
因式分解
14.3.3
十字相乘法
探索并运用十字相乘法进行因式分解;
会综合运用学过的方法对多项式进行因式分解。
学习目标
知识回顾
1.举例说明因式分解与整式乘法的关系
2.我们已经学习了哪些因式分解的方法?
提公因式法:
ma+mb+mc=m(a+b+c)
运用公式法:
a2-b2=(a+b)(a-b)
a2
±2ab+b2=(a
±b)2
(5)
3ax2+6ax+3a
(4)
x5
-
x3
(1)
x4
-
y4
(2)
(y2
+
x2
)2
-
4x2y2
(6)
2ax2+6ax+4a
(3)
x4-8x2+16
3.把下列各式因式分解:
解:(1)
x4
-
y4=(x2+y2)(x2-y2)
=
(x2+y2)(x+y)(x-y)
(2)
(y2
+
x2
)2
-
4x2y2
=(y2
+
x2
+2xy)
(y2
+
x2
-2xy)
=(x+y)2(x-y)2
(3)
x4-8x2+16=(x2-4)2
=(x+2)2(x-2)2
(4)
x5
-
x3=x3(x2-1)=x3(x+1)(x-1)
(5)
3ax2+6ax+3a=3a(x2+2x+1)
=3a(x+1)2
(6)
2ax2+6ax+4a=2a(x2+3x+2)
你认为这个多项式因式还能分解吗?
=2a(x+1)(x+2)
十字相乘法分解因式
1.(x+2)(x+1)=
x2+3x+2
3.(x-2)(x+1)=
x2-x-2
4.(x-2)(x-1)=
x2-3x+2
2.(x+2)(x-1)=
x2+x-2
5.(x+2)(x+3)=
x2+5x+6
6.(x+2)(x-3)=
x2-x-6
7.(x-2)(x+3)=
x2+x-6
8.(x-2)(x-3)=
x2-5x+6
(x+a)(x+b)
=x2+(a+b)x+ab
请直接口答计算结果:
(x+2)(x+1)
x2+3x+2
(x-2)(x+1)
x2-x-2
(x-2)(x-1)
x2-3x+2
(x+2)(x-1)
x2+x-2
(x+2)(x+3)
x2+5x+6
(x+2)(x-3)
x2-x-6
(x-2)(x+3)
x2+x-6
(x-2)(x-3)
x2-5x+6
(x+a)(x+b)
=
x2+(a+b)x+ab
=
=
=
=
=
=
=
=
1.
2.
3.
4.
5.
6.
7.
8.
(x+a)(x+b)=x2+(a+b)x+ab
观察与发现
两个一次二项式相乘的积
一个二次三项式
整式的乘法
反过来,得
x2+(a+b)x+ab=(x+a)(x+b)
一个二次三项式
两个一次二项式相乘的积
因式分解
如果二次三项式x2+px+q中的常数项系数q能分解成两个因数a、b的积,即q=ab而且一次项系数p又恰好是a、b的和,即p=a+b,那么x2+px+q就可以进行如上的因式分解。
分析∵
(+1)
×(+2)=+2
(+1)+(+2)=+3
∴
试一试:把x2+3x+2分解因式
常数项
一次项系数
十字交叉线
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法。
十字相乘法公式:
请大家记住公式
例1:
分解因式:
x2+4x+3=_______
x2-2x-3=________
(x+3)(x+1)
(x-3)(x+1)
x
x
x
x
3
1
-3
1
例2:试将
分解因式
提示:当二次项系数为-1时
,先提出负号再因式分解
。
16
6
2
+
-
-
x
x
独立练习:把下列各式分解因式
?
课堂小结
对二次三项式x2+px+q用x2+(a+b)x+ab=(x+a)(x+b)进行因式分解,应重点掌握以下问题:
2.掌握方法:拆分常数项,验证一次项.
3.符号规律:
当q>0时,a、b同号,且a、b的符号与p的符号相同;
当q<0时,a、b异号,且绝对值较大的因数与p的符号相同.
1.适用范围:只有当q=ab,且p=a+b时
才能用十字相乘法进
我
行分解。
十字相乘法分解因式(2)
本节课解决两个问题:
第一:对形如ax2+bx+c
(a≠0)的二次三项式
进行因式分解;
第二:对形如ax2+bxy+cy2
(a≠0)的二次三项式
进行因式分解;
a2
c1
c2
a1c2+a2c1=b
a1
(a1x+c1)
(a2x+c2)
=ax2+bx+c
(a≠0)
ax2+bx+c=(a1x+c1)
(a2x+c2)
(a≠0)
整式运算
因式分解
a2
c1
c2
a1c2+a2c1=b
a1
(a1x+c1y)
(a2x+c2y)
=ax2+bxy+cy2
ax2+bxy+cy2=(a1x+c1y)
(a2x+c2y)
整式运算
因式分解
例1:2x2-7x+3
总结:
1、由常数项的符号确定分解的两数的符号
2、由一次项系数确定分解的方向
3、勿忘检验分解的合理性
1
-1
-3
2
×
(-3)+(-1)
×
1=-7
2
解:原式=(2x-1)(x-3)
=
17
3
x2
+
11
x
+
10
6
x2
+
7
x
+
2
2
3
1
2
4
+
3
=
7
∴6x2+7x+2=(2x+1)(3x+2)
1
3
5
2
2
+
15
=
11
1
3
2
5
5
+
6
∴3x2+11x+10=(x+2)(3x+5)
=
–6
5
x2
–
6
xy
–
8
y2
试因式分解5x2–6xy–8y2。
这里仍然可以用十字相乘法。
1
5
–2
4
4
–
10
∴5x2–6xy–8y2
=(x–2y)(5x+4y)
简记口诀:
首尾分解,交叉相乘,求和凑中。
十字相乘法②随堂练习:
1)4a2–9a+2
2)7a2–19a–6
3)2(x2+y2)+5xy
例
.将
2(6x2
+x)
2-11(6x2
+x)
+5
分解因式
解:2(6x2
+x)2-11(6x2
+x)
+5
=
[(6x2
+x)
-5][2(6x2
+x)-1]
=
(6x2
+x-5)
(12x2
+2x-1
)
=
(6x
-5)(x
+1)
(12x2
+2x-1
)
1
2
-5
-1
-1-10=-11
6
1
-5
1
-5+6=1
练习:将下列各式分解因式
1、
7x
-13x+6
2
3、
15x
+7xy-4y
2
2
2、
-y
-4y+12
2
答案(7x-6)(x-1)
4、
x
-(a+1)
x+a
2
答案-
(y+6)(y-2)
答案
(3x-y)(5x+4y)
答案
(x-1)(x-a)
分组分解法
要发现式中隐含的条件,通过交换项的位置,添、去括号等一些变换达到因式分解的目的。
例1:因式分解
ab–ac+bd–cd
。
解:原式
=
(ab
–
ac)
+
(bd
–
cd)
=
a
(b
–
c)
+
d
(b
–
c)
=
(a
+
d)
(b
–
c)
还有别的解法吗?
分组分解法
要发现式中隐含的条件,通过交换项的位置,添、去括号等一些变换达到因式分解的目的。
例1:因式分解
ab–ac+bd–cd
。
解:原式
=
(ab
+
bd)
–
(ac
+
cd)
=
b
(a
+
d)
–
c
(a
+
d)
=
(a
+
d)
(b
–
c)
回顾例题:因式分解
x5+x4+x3+x2+x+1
。
另解:原式
=
(x5+x4)+(x3+x2)+(x+1)
=
(x+1)(x4+x2+1)
=
(x+1)(x4+2x2+1–x2)
=
(x+1)[(x2+1)2–x2]
=
(x+1)(x2+x+1)(x2–x+1)
拆项添项法
怎么结果与刚才不一样呢?
因为它还可以继续因式分解
例
因式分解
x4
+
4
解:原式
=
x4
+
4x2
+
4
–
4x2
=
(x2+2)2
–
(2x)2
=
(x2+2x+2)(x2–2x+2)
都是平方项
猜测使用完全平方公式
完全平方公式
平方差公式
拆项添项法随堂练习:
1)x4–23x2y2+y4
2)(m2–1)(n2–1)+4mn
配方法
配方法是一种特殊的拆项添项法,将多项式配成完全平方式,再用平方差公式进行分解。
因式分解
a2–b2+4a+2b+3
。
解:原式
=
(a2+4a+4)
–
(b2–2b+1)
=
(a+2)2
–
(b–1)2
=
(a+b+1)(a–b+3)
配方法
(拆项添项法)分组分解法
完全平方公式
平方差公式
