2020年冀教版八年级数学上册期末复习综合测试卷(word版 有答案)
文档属性
| 名称 | 2020年冀教版八年级数学上册期末复习综合测试卷(word版 有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 158.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 23:56:18 | ||
图片预览




文档简介
冀教版八年级上册期末复习综合测试卷
(时间:90分钟 满分:100分)
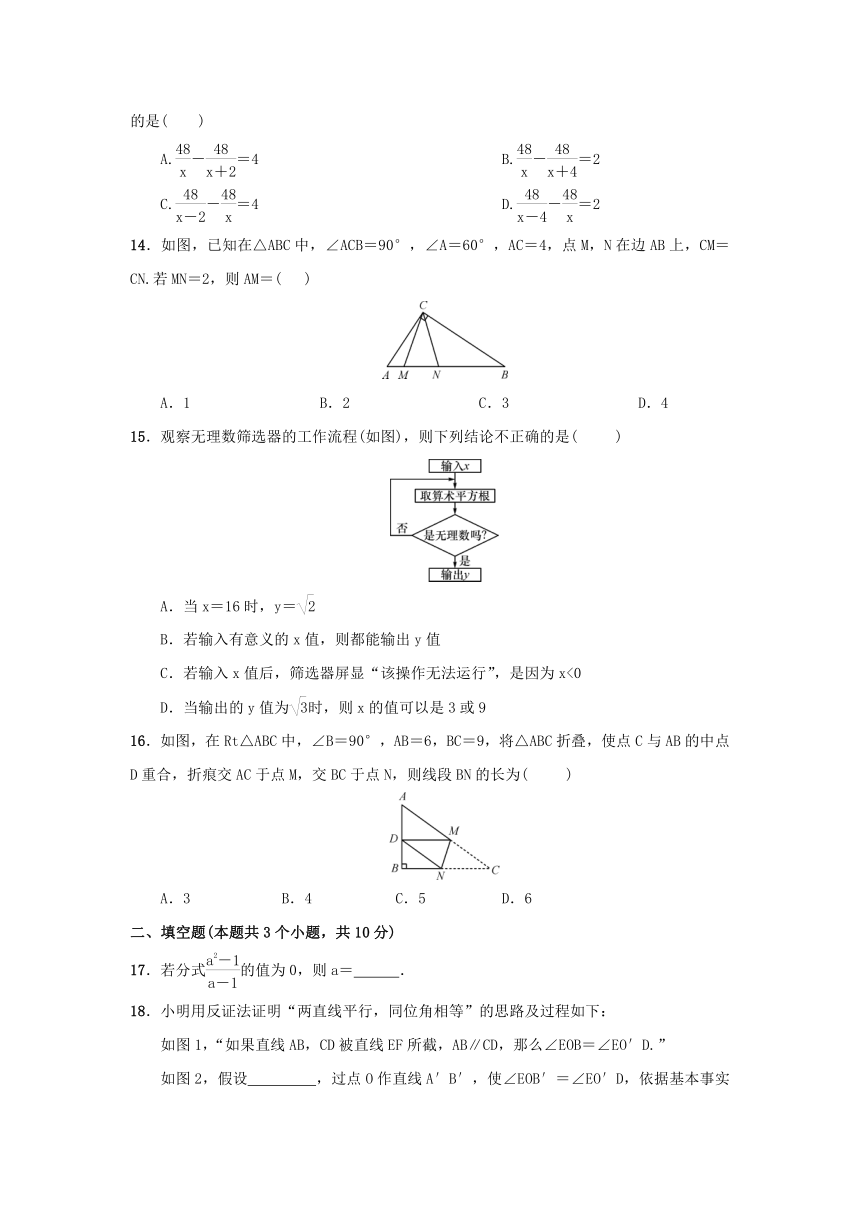
一、选择题(本大题有16个小题,共32分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.
下列图案中,既是轴对称图形,又是中心对称图形的是(
)
2.使二次根式有意义的x的取值范围是(
)
A.x≠1
B.x>1
C.x≤1
D.x≥1
3.由四舍五入得到的近似数88.35万,是精确到(
)
A.十分位
B.百分位
C.百位
D.十位
4.下列说法正确的是(
)
A.1的平方根是1
B.-8的立方根是-2
C.是无理数
D.=-2
5.如图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB,AD沿着角的两边放下,沿AC画一条射线AE,AE就是这个角的平分线,操作过程中用到的三角形全等的判定方法是(
)
A.SSS
B.SAS
C.ASA
D.AAS
6.一个等腰三角形的两边长分别是4和9,则它的周长为(
)
A.17
B.18
C.22
D.17或22
7.如图,Rt△ABC的直角边AB在数轴上,点A表示的实数为0,以A为圆心,AC的长为半径作弧交数轴的负半轴于点D.若CB=1,AB=2,则点D表示的实数为(
)
A.
B.-
C.
D.-
8.如图,点D为Rt△ABC斜边上的中点,连接CD.若∠CDB=110°,则∠A=(
)
A.30°
B.35°
C.40°
D.55°
下列运算正确的是(
)
A.1+=
B.+=1
C.a÷·=a
D.+=
10.如图,已知△ABC,按以下步骤作图:①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于M,N两点;②作直线MN交AB于点D,连接CD.若∠B=30°,∠A=55°,则∠ACD的度数为(
)
A.65°
B.60°
C.55°
D.45°
11.
如图,AD为△ABC的角平分线,AC=3.5,AB=5.若△ACD的面积为3.5,则△BDA的面积为(
)
A.2.5
B.3.5
C.5
D.10
12.由下列条件不能判定△ABC为直角三角形的是(
)
A.∠A-∠B=∠C
B.∠A∶∠B∶∠C=3∶4∶5
C.(b+c)(b-c)=a2
D.AD为△ABC的中线,且BC=2AD
13.为了确保冬季供暖正常,学校门前有48米的管道需要维修保养.开工后,每小时比原计划多维修2米,结果提前4小时完成任务.若设原计划每小时维修x米,则下列方程正确的是(
)
A.-=4
B.-=2
C.-=4
D.-=2
14.如图,已知在△ABC中,∠ACB=90°,∠A=60°,AC=4,点M,N在边AB上,CM=CN.若MN=2,则AM=(
)
A.1
B.2
C.3
D.4
15.观察无理数筛选器的工作流程(如图),则下列结论不正确的是(
)
A.当x=16时,y=
B.若输入有意义的x值,则都能输出y值
C.若输入x值后,筛选器屏显“该操作无法运行”,是因为x<0
D.当输出的y值为时,则x的值可以是3或9
16.如图,在Rt△ABC中,∠B=90°,AB=6,BC=9,将△ABC折叠,使点C与AB的中点D重合,折痕交AC于点M,交BC于点N,则线段BN的长为(
)
A.3
B.4
C.5
D.6
二、填空题(本题共3个小题,共10分)
17.若分式的值为0,则a=
.
18.小明用反证法证明“两直线平行,同位角相等”的思路及过程如下:
如图1,“如果直线AB,CD被直线EF所截,AB∥CD,那么∠EOB=∠EO′D.”
如图2,假设
,过点O作直线A′B′,使∠EOB′=∠EO′D,依据基本事实“同位角相等,两直线平行”,可得A′B′∥CD.这样过点O就有两条直线AB,A′B′都平行于直线CD,这与基本事实
矛盾,这说明假设不成立,于是有∠EOB=∠EO′D.
19.甲、乙、丙三位同学在研究一道问题:一个等腰三角形可以被一条直线分割成两个等腰三角形,求该等腰三角形顶角的度数.
甲说:“顶角是底角2倍的等腰三角形可以分割成两个等腰三角形,如图1.”
乙说:“底角是顶角2倍的等腰三角形也可以分割成两个等腰三角形,如图2.”
丙说:“除了‘2倍’,‘■倍’的也行,我发现了另外两种等腰三角形也可分割成两个等腰三角形.”
请你写出丙同学所说的两种等腰三角形顶角的度数:
三、解答题(本大题共7个小题,共58分.解答应写出文字说明、证明过程或演算步骤)
20.(本题满分6分)计算下列各式:
(1)-+;
(2)(+3)(-2).
21.(本题满分8分)(1)求值:(1-)÷,其中a=100.
(2)解方程:=+3.
22.(本题满分8分)如图,在△ABC中,AB=AC,∠A=120°,点M为BC边的中点,点P为AC边上任意一点,连接PM,并延长PM至点Q,恰使BQ∥AC.
(1)求证:BQ=CP.
(2)当△BQM为等腰三角形时,直接写出∠PMC的度数.
23.(本题满分8分)从某地到北京的路程约是450
km,可乘坐高铁或自驾车.已知高铁的平均速度(km/h)是自驾车平均速度(km/h)的2.5倍,且乘坐高铁所需时间比自驾车所需时间少3
h,求高铁的平均速度.
24.(本题满分7分)在如图所示的方格纸中,每个方格都是边长为1个单位长度的小正方形,△ABC的三个顶点都在格点上(每个小正方形的顶点叫做格点).
(1)AC的长为.
(2)在BC上找一点P,使∠CAP=45°(在网格中直接描出点P).
(3)在图中画出△AB1C1,使△AB1C1与△ABC关于点A成中心对称.
(4)若点Q是该方格纸中的一个格点,且满足△BCQ是轴对称图形,这样的点Q共有9个.
25.(本题满分10分)阅读材料1:
对于两个正实数a,b,由于(-)2≥0,所以()2-2·+()2≥0,即a-2+b≥0.所以a+b≥2,并且当a=b时,a+b=2.
阅读材料2:
因为=+=x+,若x>0,则>0.
由阅读材料1可得:x+≥2=2,即的最小值是2,只有当x=时,即x=1时,取得最小值.
请根据以上阅读材料,解答以下问题:
(1)比较大小:
x2+1
2x(其中x≥1),
当x<-1时,-x->2,x+
-2.
(2)若代数式可变形为x+n+,求常数n的值.
(3)仿照(2)代数式的变形填空:
∵
,∴当x=
时取得最小值,最小值为3.
26.(本题满分11分)如图1,正方形AEFG的边长为2,在Rt△ABD中,∠BAD=90°,AB=AD=2.连接DG,EB.
(1)求证:BE=DG.
(2)如图2,将Rt△ABD绕点A顺时针旋转,使点B恰好落在线段DG上,过点D作DA′⊥AD,且DA′=DA,连接AA′.
①求证:DG垂直平分AA′.
②求∠BAG的度数.
答案
一、选择题(本大题有16个小题,共32分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.
下列图案中,既是轴对称图形,又是中心对称图形的是(
D
)
2.使二次根式有意义的x的取值范围是(
D
)
A.x≠1
B.x>1
C.x≤1
D.x≥1
3.由四舍五入得到的近似数88.35万,是精确到(
C
)
A.十分位
B.百分位
C.百位
D.十位
4.下列说法正确的是(
B
)
A.1的平方根是1
B.-8的立方根是-2
C.是无理数
D.=-2
5.如图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB,AD沿着角的两边放下,沿AC画一条射线AE,AE就是这个角的平分线,操作过程中用到的三角形全等的判定方法是(
A
)
A.SSS
B.SAS
C.ASA
D.AAS
6.一个等腰三角形的两边长分别是4和9,则它的周长为(
C
)
A.17
B.18
C.22
D.17或22
7.如图,Rt△ABC的直角边AB在数轴上,点A表示的实数为0,以A为圆心,AC的长为半径作弧交数轴的负半轴于点D.若CB=1,AB=2,则点D表示的实数为(
B
)
A.
B.-
C.
D.-
8.如图,点D为Rt△ABC斜边上的中点,连接CD.若∠CDB=110°,则∠A=(
D
)
A.30°
B.35°
C.40°
D.55°
9.下列运算正确的是(
B
)
A.1+=
B.+=1
C.a÷·=a
D.+=
10.如图,已知△ABC,按以下步骤作图:①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于M,N两点;②作直线MN交AB于点D,连接CD.若∠B=30°,∠A=55°,则∠ACD的度数为(
A
)
A.65°
B.60°
C.55°
D.45°
11.
如图,AD为△ABC的角平分线,AC=3.5,AB=5.若△ACD的面积为3.5,则△BDA的面积为(
C
)
A.2.5
B.3.5
C.5
D.10
12.由下列条件不能判定△ABC为直角三角形的是(
B
)
A.∠A-∠B=∠C
B.∠A∶∠B∶∠C=3∶4∶5
C.(b+c)(b-c)=a2
D.AD为△ABC的中线,且BC=2AD
13.为了确保冬季供暖正常,学校门前有48米的管道需要维修保养.开工后,每小时比原计划多维修2米,结果提前4小时完成任务.若设原计划每小时维修x米,则下列方程正确的是(
A
)
A.-=4
B.-=2
C.-=4
D.-=2
14.如图,已知在△ABC中,∠ACB=90°,∠A=60°,AC=4,点M,N在边AB上,CM=CN.若MN=2,则AM=(
A
)
A.1
B.2
C.3
D.4
15.观察无理数筛选器的工作流程(如图),则下列结论不正确的是(
B
)
A.当x=16时,y=
B.若输入有意义的x值,则都能输出y值
C.若输入x值后,筛选器屏显“该操作无法运行”,是因为x<0
D.当输出的y值为时,则x的值可以是3或9
16.如图,在Rt△ABC中,∠B=90°,AB=6,BC=9,将△ABC折叠,使点C与AB的中点D重合,折痕交AC于点M,交BC于点N,则线段BN的长为(
B
)
A.3
B.4
C.5
D.6
二、填空题(本题共3个小题,共10分)
17.若分式的值为0,则a=-1.
18.小明用反证法证明“两直线平行,同位角相等”的思路及过程如下:
如图1,“如果直线AB,CD被直线EF所截,AB∥CD,那么∠EOB=∠EO′D.”
如图2,假设∠EOB≠∠EO′D,过点O作直线A′B′,使∠EOB′=∠EO′D,依据基本事实“同位角相等,两直线平行”,可得A′B′∥CD.这样过点O就有两条直线AB,A′B′都平行于直线CD,这与基本事实经过直线外一点,有且只有一条直线与已知直线平行矛盾,这说明假设不成立,于是有∠EOB=∠EO′D.
19.甲、乙、丙三位同学在研究一道问题:一个等腰三角形可以被一条直线分割成两个等腰三角形,求该等腰三角形顶角的度数.
甲说:“顶角是底角2倍的等腰三角形可以分割成两个等腰三角形,如图1.”
乙说:“底角是顶角2倍的等腰三角形也可以分割成两个等腰三角形,如图2.”
丙说:“除了‘2倍’,‘■倍’的也行,我发现了另外两种等腰三角形也可分割成两个等腰三角形.”
请你写出丙同学所说的两种等腰三角形顶角的度数:108°、.
三、解答题(本大题共7个小题,共58分.解答应写出文字说明、证明过程或演算步骤)
20.(本题满分6分)计算下列各式:
(1)-+;
解:原式=3-2+
=.
(2)(+3)(-2).
解:原式=5-2+3-6
=-1.
21.(本题满分8分)(1)求值:(1-)÷,其中a=100.
解:原式=·
=a-1.
当a=100时,原式=100-1=99.
(2)解方程:=+3.
解:方程两边同乘(x-1),得
2x=1+3(x-1),
解得x=2.
检验:当x=2时,x-1≠0.
∴x=2是原分式方程的解.
22.(本题满分8分)如图,在△ABC中,AB=AC,∠A=120°,点M为BC边的中点,点P为AC边上任意一点,连接PM,并延长PM至点Q,恰使BQ∥AC.
(1)求证:BQ=CP.
(2)当△BQM为等腰三角形时,直接写出∠PMC的度数.
解:(1)证明:∵BQ∥AC,
∴∠C=∠QBM.
∵M为BC边的中点,∴BM=CM.
在△CPM和△BQM中,
∴△CPM≌△BQM(ASA).
∴BQ=CP.
(2)30°或75°.
23.(本题满分8分)从某地到北京的路程约是450
km,可乘坐高铁或自驾车.已知高铁的平均速度(km/h)是自驾车平均速度(km/h)的2.5倍,且乘坐高铁所需时间比自驾车所需时间少3
h,求高铁的平均速度.
解:设自驾车的平均速度为x
km/h,则高铁的平均速度为2.5x
km/h,根据题意,得
-=3,解得x=90.
经检验,x=90是原分式方程的解,且符合题意.
则2.5×90=225(km/h).
答:高铁的平均速度为225
km/h.
24.(本题满分7分)在如图所示的方格纸中,每个方格都是边长为1个单位长度的小正方形,△ABC的三个顶点都在格点上(每个小正方形的顶点叫做格点).
(1)AC的长为.
(2)在BC上找一点P,使∠CAP=45°(在网格中直接描出点P).
(3)在图中画出△AB1C1,使△AB1C1与△ABC关于点A成中心对称.
(4)若点Q是该方格纸中的一个格点,且满足△BCQ是轴对称图形,这样的点Q共有9个.
解:(2)(3)如图所示.
25.(本题满分10分)阅读材料1:
对于两个正实数a,b,由于(-)2≥0,所以()2-2·+()2≥0,即a-2+b≥0.所以a+b≥2,并且当a=b时,a+b=2.
阅读材料2:
因为=+=x+,若x>0,则>0.
由阅读材料1可得:x+≥2=2,即的最小值是2,只有当x=时,即x=1时,取得最小值.
请根据以上阅读材料,解答以下问题:
(1)比较大小:
x2+1≥2x(其中x≥1),
当x<-1时,-x->2,x+<-2.
(2)若代数式可变形为x+n+,求常数n的值.
(3)仿照(2)代数式的变形填空:
∵=1+(+1)+,∴当x=0时取得最小值,最小值为3.
解:==++=x+2+=x+n+,
所以n=2.
26.(本题满分11分)如图1,正方形AEFG的边长为2,在Rt△ABD中,∠BAD=90°,AB=AD=2.连接DG,EB.
(1)求证:BE=DG.
(2)如图2,将Rt△ABD绕点A顺时针旋转,使点B恰好落在线段DG上,过点D作DA′⊥AD,且DA′=DA,连接AA′.
①求证:DG垂直平分AA′.
②求∠BAG的度数.
解:(1)证明:∵正方形AEFG的四个角都是直角,
∴∠GAE=∠BAD=90°,∠GAD=90°+∠BAG=∠EAB.
又∵AD=AB,AG=AE,∴△ABE≌△ADG(SAS).∴BE=DG.
(2)①设DG与AA′交于点O,∵DA′⊥AD,∴∠ADA′=90°.
又∵在△ABD中,∠BAD=90°,AB=AD,
∴∠ADB=45°.∴∠A′DG=90°-45°=45°,即∠ADB=∠A′DG.
又∵DA′=DA,∴DO是等腰Rt△ADA′底边AA′的中线和高.∴DG垂直平分AA′.
②连接A′G.由①知DG垂直平分AA′,∴A′G=AG.
在
Rt△ADA′中,DA′=DA=2,
∴AA′==2.∴AA′=AG=A′G,即△AGA′是等边三角形.∴∠A′AG=60°.
又∵在△ADA′中,∠ADA′=90°,DA′=DA,∴∠A′AD=45°.∴∠A′AB=90°-45°=45°.
∴∠BAG=∠A′AG-∠A′AB=60°-45°=15°.
(时间:90分钟 满分:100分)
一、选择题(本大题有16个小题,共32分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.
下列图案中,既是轴对称图形,又是中心对称图形的是(
)
2.使二次根式有意义的x的取值范围是(
)
A.x≠1
B.x>1
C.x≤1
D.x≥1
3.由四舍五入得到的近似数88.35万,是精确到(
)
A.十分位
B.百分位
C.百位
D.十位
4.下列说法正确的是(
)
A.1的平方根是1
B.-8的立方根是-2
C.是无理数
D.=-2
5.如图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB,AD沿着角的两边放下,沿AC画一条射线AE,AE就是这个角的平分线,操作过程中用到的三角形全等的判定方法是(
)
A.SSS
B.SAS
C.ASA
D.AAS
6.一个等腰三角形的两边长分别是4和9,则它的周长为(
)
A.17
B.18
C.22
D.17或22
7.如图,Rt△ABC的直角边AB在数轴上,点A表示的实数为0,以A为圆心,AC的长为半径作弧交数轴的负半轴于点D.若CB=1,AB=2,则点D表示的实数为(
)
A.
B.-
C.
D.-
8.如图,点D为Rt△ABC斜边上的中点,连接CD.若∠CDB=110°,则∠A=(
)
A.30°
B.35°
C.40°
D.55°
下列运算正确的是(
)
A.1+=
B.+=1
C.a÷·=a
D.+=
10.如图,已知△ABC,按以下步骤作图:①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于M,N两点;②作直线MN交AB于点D,连接CD.若∠B=30°,∠A=55°,则∠ACD的度数为(
)
A.65°
B.60°
C.55°
D.45°
11.
如图,AD为△ABC的角平分线,AC=3.5,AB=5.若△ACD的面积为3.5,则△BDA的面积为(
)
A.2.5
B.3.5
C.5
D.10
12.由下列条件不能判定△ABC为直角三角形的是(
)
A.∠A-∠B=∠C
B.∠A∶∠B∶∠C=3∶4∶5
C.(b+c)(b-c)=a2
D.AD为△ABC的中线,且BC=2AD
13.为了确保冬季供暖正常,学校门前有48米的管道需要维修保养.开工后,每小时比原计划多维修2米,结果提前4小时完成任务.若设原计划每小时维修x米,则下列方程正确的是(
)
A.-=4
B.-=2
C.-=4
D.-=2
14.如图,已知在△ABC中,∠ACB=90°,∠A=60°,AC=4,点M,N在边AB上,CM=CN.若MN=2,则AM=(
)
A.1
B.2
C.3
D.4
15.观察无理数筛选器的工作流程(如图),则下列结论不正确的是(
)
A.当x=16时,y=
B.若输入有意义的x值,则都能输出y值
C.若输入x值后,筛选器屏显“该操作无法运行”,是因为x<0
D.当输出的y值为时,则x的值可以是3或9
16.如图,在Rt△ABC中,∠B=90°,AB=6,BC=9,将△ABC折叠,使点C与AB的中点D重合,折痕交AC于点M,交BC于点N,则线段BN的长为(
)
A.3
B.4
C.5
D.6
二、填空题(本题共3个小题,共10分)
17.若分式的值为0,则a=
.
18.小明用反证法证明“两直线平行,同位角相等”的思路及过程如下:
如图1,“如果直线AB,CD被直线EF所截,AB∥CD,那么∠EOB=∠EO′D.”
如图2,假设
,过点O作直线A′B′,使∠EOB′=∠EO′D,依据基本事实“同位角相等,两直线平行”,可得A′B′∥CD.这样过点O就有两条直线AB,A′B′都平行于直线CD,这与基本事实
矛盾,这说明假设不成立,于是有∠EOB=∠EO′D.
19.甲、乙、丙三位同学在研究一道问题:一个等腰三角形可以被一条直线分割成两个等腰三角形,求该等腰三角形顶角的度数.
甲说:“顶角是底角2倍的等腰三角形可以分割成两个等腰三角形,如图1.”
乙说:“底角是顶角2倍的等腰三角形也可以分割成两个等腰三角形,如图2.”
丙说:“除了‘2倍’,‘■倍’的也行,我发现了另外两种等腰三角形也可分割成两个等腰三角形.”
请你写出丙同学所说的两种等腰三角形顶角的度数:
三、解答题(本大题共7个小题,共58分.解答应写出文字说明、证明过程或演算步骤)
20.(本题满分6分)计算下列各式:
(1)-+;
(2)(+3)(-2).
21.(本题满分8分)(1)求值:(1-)÷,其中a=100.
(2)解方程:=+3.
22.(本题满分8分)如图,在△ABC中,AB=AC,∠A=120°,点M为BC边的中点,点P为AC边上任意一点,连接PM,并延长PM至点Q,恰使BQ∥AC.
(1)求证:BQ=CP.
(2)当△BQM为等腰三角形时,直接写出∠PMC的度数.
23.(本题满分8分)从某地到北京的路程约是450
km,可乘坐高铁或自驾车.已知高铁的平均速度(km/h)是自驾车平均速度(km/h)的2.5倍,且乘坐高铁所需时间比自驾车所需时间少3
h,求高铁的平均速度.
24.(本题满分7分)在如图所示的方格纸中,每个方格都是边长为1个单位长度的小正方形,△ABC的三个顶点都在格点上(每个小正方形的顶点叫做格点).
(1)AC的长为.
(2)在BC上找一点P,使∠CAP=45°(在网格中直接描出点P).
(3)在图中画出△AB1C1,使△AB1C1与△ABC关于点A成中心对称.
(4)若点Q是该方格纸中的一个格点,且满足△BCQ是轴对称图形,这样的点Q共有9个.
25.(本题满分10分)阅读材料1:
对于两个正实数a,b,由于(-)2≥0,所以()2-2·+()2≥0,即a-2+b≥0.所以a+b≥2,并且当a=b时,a+b=2.
阅读材料2:
因为=+=x+,若x>0,则>0.
由阅读材料1可得:x+≥2=2,即的最小值是2,只有当x=时,即x=1时,取得最小值.
请根据以上阅读材料,解答以下问题:
(1)比较大小:
x2+1
2x(其中x≥1),
当x<-1时,-x->2,x+
-2.
(2)若代数式可变形为x+n+,求常数n的值.
(3)仿照(2)代数式的变形填空:
∵
,∴当x=
时取得最小值,最小值为3.
26.(本题满分11分)如图1,正方形AEFG的边长为2,在Rt△ABD中,∠BAD=90°,AB=AD=2.连接DG,EB.
(1)求证:BE=DG.
(2)如图2,将Rt△ABD绕点A顺时针旋转,使点B恰好落在线段DG上,过点D作DA′⊥AD,且DA′=DA,连接AA′.
①求证:DG垂直平分AA′.
②求∠BAG的度数.
答案
一、选择题(本大题有16个小题,共32分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.
下列图案中,既是轴对称图形,又是中心对称图形的是(
D
)
2.使二次根式有意义的x的取值范围是(
D
)
A.x≠1
B.x>1
C.x≤1
D.x≥1
3.由四舍五入得到的近似数88.35万,是精确到(
C
)
A.十分位
B.百分位
C.百位
D.十位
4.下列说法正确的是(
B
)
A.1的平方根是1
B.-8的立方根是-2
C.是无理数
D.=-2
5.如图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB,AD沿着角的两边放下,沿AC画一条射线AE,AE就是这个角的平分线,操作过程中用到的三角形全等的判定方法是(
A
)
A.SSS
B.SAS
C.ASA
D.AAS
6.一个等腰三角形的两边长分别是4和9,则它的周长为(
C
)
A.17
B.18
C.22
D.17或22
7.如图,Rt△ABC的直角边AB在数轴上,点A表示的实数为0,以A为圆心,AC的长为半径作弧交数轴的负半轴于点D.若CB=1,AB=2,则点D表示的实数为(
B
)
A.
B.-
C.
D.-
8.如图,点D为Rt△ABC斜边上的中点,连接CD.若∠CDB=110°,则∠A=(
D
)
A.30°
B.35°
C.40°
D.55°
9.下列运算正确的是(
B
)
A.1+=
B.+=1
C.a÷·=a
D.+=
10.如图,已知△ABC,按以下步骤作图:①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于M,N两点;②作直线MN交AB于点D,连接CD.若∠B=30°,∠A=55°,则∠ACD的度数为(
A
)
A.65°
B.60°
C.55°
D.45°
11.
如图,AD为△ABC的角平分线,AC=3.5,AB=5.若△ACD的面积为3.5,则△BDA的面积为(
C
)
A.2.5
B.3.5
C.5
D.10
12.由下列条件不能判定△ABC为直角三角形的是(
B
)
A.∠A-∠B=∠C
B.∠A∶∠B∶∠C=3∶4∶5
C.(b+c)(b-c)=a2
D.AD为△ABC的中线,且BC=2AD
13.为了确保冬季供暖正常,学校门前有48米的管道需要维修保养.开工后,每小时比原计划多维修2米,结果提前4小时完成任务.若设原计划每小时维修x米,则下列方程正确的是(
A
)
A.-=4
B.-=2
C.-=4
D.-=2
14.如图,已知在△ABC中,∠ACB=90°,∠A=60°,AC=4,点M,N在边AB上,CM=CN.若MN=2,则AM=(
A
)
A.1
B.2
C.3
D.4
15.观察无理数筛选器的工作流程(如图),则下列结论不正确的是(
B
)
A.当x=16时,y=
B.若输入有意义的x值,则都能输出y值
C.若输入x值后,筛选器屏显“该操作无法运行”,是因为x<0
D.当输出的y值为时,则x的值可以是3或9
16.如图,在Rt△ABC中,∠B=90°,AB=6,BC=9,将△ABC折叠,使点C与AB的中点D重合,折痕交AC于点M,交BC于点N,则线段BN的长为(
B
)
A.3
B.4
C.5
D.6
二、填空题(本题共3个小题,共10分)
17.若分式的值为0,则a=-1.
18.小明用反证法证明“两直线平行,同位角相等”的思路及过程如下:
如图1,“如果直线AB,CD被直线EF所截,AB∥CD,那么∠EOB=∠EO′D.”
如图2,假设∠EOB≠∠EO′D,过点O作直线A′B′,使∠EOB′=∠EO′D,依据基本事实“同位角相等,两直线平行”,可得A′B′∥CD.这样过点O就有两条直线AB,A′B′都平行于直线CD,这与基本事实经过直线外一点,有且只有一条直线与已知直线平行矛盾,这说明假设不成立,于是有∠EOB=∠EO′D.
19.甲、乙、丙三位同学在研究一道问题:一个等腰三角形可以被一条直线分割成两个等腰三角形,求该等腰三角形顶角的度数.
甲说:“顶角是底角2倍的等腰三角形可以分割成两个等腰三角形,如图1.”
乙说:“底角是顶角2倍的等腰三角形也可以分割成两个等腰三角形,如图2.”
丙说:“除了‘2倍’,‘■倍’的也行,我发现了另外两种等腰三角形也可分割成两个等腰三角形.”
请你写出丙同学所说的两种等腰三角形顶角的度数:108°、.
三、解答题(本大题共7个小题,共58分.解答应写出文字说明、证明过程或演算步骤)
20.(本题满分6分)计算下列各式:
(1)-+;
解:原式=3-2+
=.
(2)(+3)(-2).
解:原式=5-2+3-6
=-1.
21.(本题满分8分)(1)求值:(1-)÷,其中a=100.
解:原式=·
=a-1.
当a=100时,原式=100-1=99.
(2)解方程:=+3.
解:方程两边同乘(x-1),得
2x=1+3(x-1),
解得x=2.
检验:当x=2时,x-1≠0.
∴x=2是原分式方程的解.
22.(本题满分8分)如图,在△ABC中,AB=AC,∠A=120°,点M为BC边的中点,点P为AC边上任意一点,连接PM,并延长PM至点Q,恰使BQ∥AC.
(1)求证:BQ=CP.
(2)当△BQM为等腰三角形时,直接写出∠PMC的度数.
解:(1)证明:∵BQ∥AC,
∴∠C=∠QBM.
∵M为BC边的中点,∴BM=CM.
在△CPM和△BQM中,
∴△CPM≌△BQM(ASA).
∴BQ=CP.
(2)30°或75°.
23.(本题满分8分)从某地到北京的路程约是450
km,可乘坐高铁或自驾车.已知高铁的平均速度(km/h)是自驾车平均速度(km/h)的2.5倍,且乘坐高铁所需时间比自驾车所需时间少3
h,求高铁的平均速度.
解:设自驾车的平均速度为x
km/h,则高铁的平均速度为2.5x
km/h,根据题意,得
-=3,解得x=90.
经检验,x=90是原分式方程的解,且符合题意.
则2.5×90=225(km/h).
答:高铁的平均速度为225
km/h.
24.(本题满分7分)在如图所示的方格纸中,每个方格都是边长为1个单位长度的小正方形,△ABC的三个顶点都在格点上(每个小正方形的顶点叫做格点).
(1)AC的长为.
(2)在BC上找一点P,使∠CAP=45°(在网格中直接描出点P).
(3)在图中画出△AB1C1,使△AB1C1与△ABC关于点A成中心对称.
(4)若点Q是该方格纸中的一个格点,且满足△BCQ是轴对称图形,这样的点Q共有9个.
解:(2)(3)如图所示.
25.(本题满分10分)阅读材料1:
对于两个正实数a,b,由于(-)2≥0,所以()2-2·+()2≥0,即a-2+b≥0.所以a+b≥2,并且当a=b时,a+b=2.
阅读材料2:
因为=+=x+,若x>0,则>0.
由阅读材料1可得:x+≥2=2,即的最小值是2,只有当x=时,即x=1时,取得最小值.
请根据以上阅读材料,解答以下问题:
(1)比较大小:
x2+1≥2x(其中x≥1),
当x<-1时,-x->2,x+<-2.
(2)若代数式可变形为x+n+,求常数n的值.
(3)仿照(2)代数式的变形填空:
∵=1+(+1)+,∴当x=0时取得最小值,最小值为3.
解:==++=x+2+=x+n+,
所以n=2.
26.(本题满分11分)如图1,正方形AEFG的边长为2,在Rt△ABD中,∠BAD=90°,AB=AD=2.连接DG,EB.
(1)求证:BE=DG.
(2)如图2,将Rt△ABD绕点A顺时针旋转,使点B恰好落在线段DG上,过点D作DA′⊥AD,且DA′=DA,连接AA′.
①求证:DG垂直平分AA′.
②求∠BAG的度数.
解:(1)证明:∵正方形AEFG的四个角都是直角,
∴∠GAE=∠BAD=90°,∠GAD=90°+∠BAG=∠EAB.
又∵AD=AB,AG=AE,∴△ABE≌△ADG(SAS).∴BE=DG.
(2)①设DG与AA′交于点O,∵DA′⊥AD,∴∠ADA′=90°.
又∵在△ABD中,∠BAD=90°,AB=AD,
∴∠ADB=45°.∴∠A′DG=90°-45°=45°,即∠ADB=∠A′DG.
又∵DA′=DA,∴DO是等腰Rt△ADA′底边AA′的中线和高.∴DG垂直平分AA′.
②连接A′G.由①知DG垂直平分AA′,∴A′G=AG.
在
Rt△ADA′中,DA′=DA=2,
∴AA′==2.∴AA′=AG=A′G,即△AGA′是等边三角形.∴∠A′AG=60°.
又∵在△ADA′中,∠ADA′=90°,DA′=DA,∴∠A′AD=45°.∴∠A′AB=90°-45°=45°.
∴∠BAG=∠A′AG-∠A′AB=60°-45°=15°.
同课章节目录
