人教版数学八年级上册:13.1.1 轴对称 同步练习 (word版,含答案)
文档属性
| 名称 | 人教版数学八年级上册:13.1.1 轴对称 同步练习 (word版,含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 358.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 08:30:59 | ||
图片预览

文档简介
人教版数学八年级上册
第十三章
13.1
轴对称
同步练习
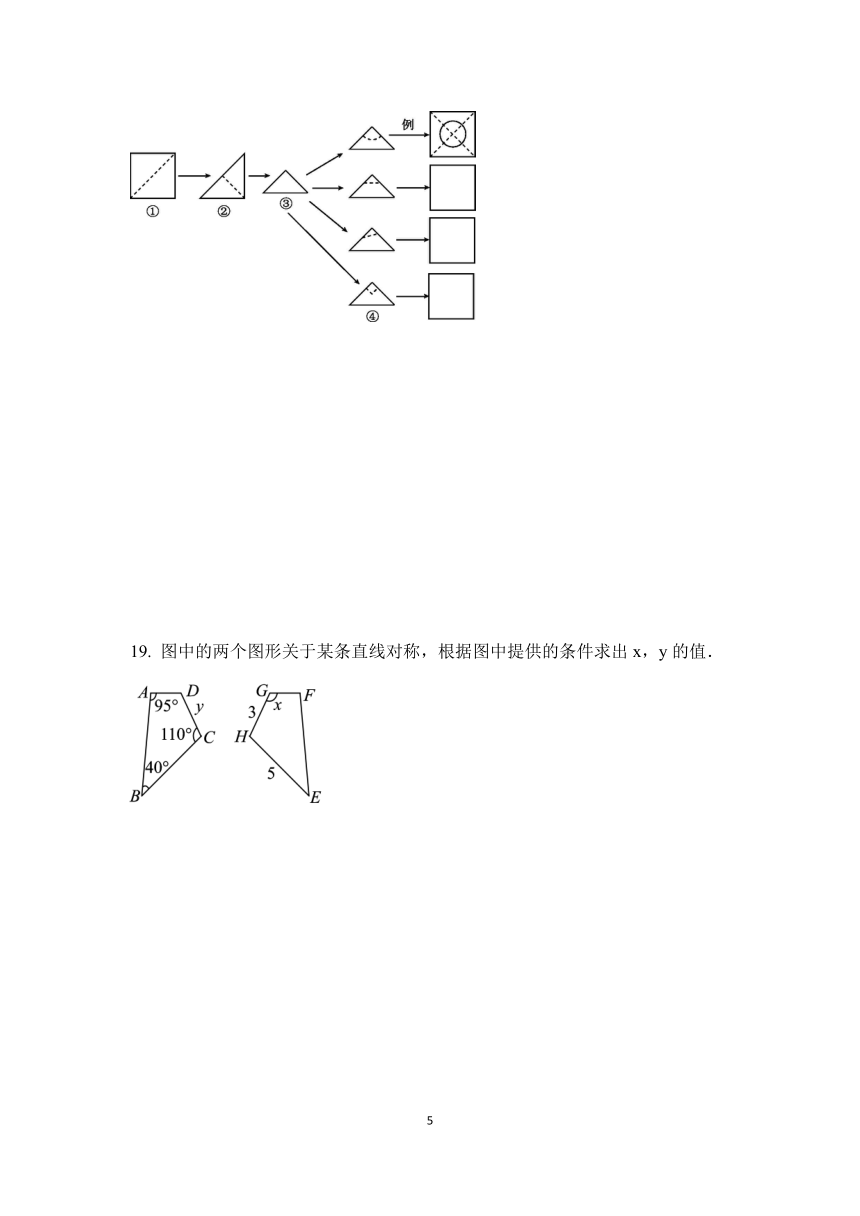
一、选择题
1.下列银行标志中,是轴对称图形的是(
)
A.徽商银行
B.中国建设银行
C.交通银行
D.中国银行
2.
如下图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
A.①???
?
B.②???
?
C.⑤???
?
D.⑥
3.
如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说
法不一定正确的是( )
A.AC=A'C'
B.BO=B'O
C.AA'⊥MN
D.AB=B'C'
4.
下列图形中,不是轴对称图形的是(
)
5.
在平面直角坐标系中,作点A(3,4)关于x轴的对称点A′,再将点A′向左平移6个单位长度,得到点B,则点B的坐标为( )
A.(4,-3)
B.(-4,3)
C.(-3,4)
D.(-3,-4)
6.
如图,线段AB与A′B′(AB=A′B′)不关于直线l成轴对称的是( )
7.
已知,如图,点P关于OA、OB的对称点分别是P1,P2,线段P1P2分别交OA、OB于D、C,P1P2=6cm,则△PCD的周长为( )
A.3cm
B.6cm
C.12cm
D.无法确定
8.
如图所示的五角星是轴对称图形,它的对称轴共有( )
A.1条
B.3条
C.5条
D.无数条
9.
将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图4,将图4的纸片展开铺平,再得到的图案是(
)
二、填空题
10.
如图所示的4组图形中,左右两个图形成轴对称的是第________组(填序号).
11.
如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有
个.
12.
如图是某时刻在镜子中看到准确时钟的情况,则实际时间是???????
?
13.
在①线段、②角、③圆、④长方形、⑤梯形、⑥三角形、⑦等边三角形中,是轴对称图形的有
(只填序号)
14.
若点A(1﹣m,6)与B(2+n,6)关于某坐标轴对称,则m﹣n=
.
15.
如图,△ABO是关于y轴对称的轴对称图形,点A的坐标为(-2,3),则点B的坐标为________.
16.
如图所示,分别将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为E,F,G,H的四个图形,则剪前与剪后拼接的图形的对应关系是:A与________对应,B与________对应,C与________对应,D与________对应.
三、解答题
17.
如图,在平面直角坐标系中,
(1)描出A(-
4,3)B(-1,0)C(-2,3)三点.
(2)△ABC的面积是????????
(3)作出△ABC关于x轴的对称图形.
18.
小强拿几张正方形的纸(如图4①),沿虚线对折一次得到图②,再沿虚线对折一次得到图③,然后用剪刀沿图④中不同位置的虚线剪去中心的一块,请参照例图,在后面的正方形中画出图④的纸片打开后的形状.(不写作法,保留作图痕迹)
19.
图中的两个图形关于某条直线对称,根据图中提供的条件求出x,y的值.
20.
如图,Rt△ABC的顶点A,B,C关于直线MN的对称点分别为A',B',C',其中∠A=90°,AC=8
cm,点C,B,A'在同一条直线上,且A'C=12
cm.
(1)求△A'B'C'的周长;
(2)求△A'CC'的面积.
21.
如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(﹣3,2).请按要求分别完成下列各小题:
(1)把△ABC向下平移4个单位得到△A1B1C1,画出△A1B1C1,点A1的坐标是
;
(2)画出△ABC关于y轴对称的△A2B2C2;点C2的坐标是
;
(3)求△ABC的面积.
22.
如图,直线AD和CE是△ABC的两条对称轴,AD和CE相交于点O,OD
与OE有什么数量关系?请说明理由.
23.
已知点A(2m+n,2),B
(1,n﹣m),当m、n分别为何值时,
(1)A、B关于x轴对称;
(2)A、B关于y轴对称.
人教版数学八年级上册
第十三章
13.1
轴对称
同步练习--参考答案
一、选择题
1.下列银行标志中,是轴对称图形的是(
)
A.徽商银行
B.中国建设银行
C.交通银行
D.中国银行
【答案】D
2.
如下图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
A.①???
?
B.②???
?
C.⑤???
?
D.⑥
【答案】答案为:B
3.
如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说
法不一定正确的是( )
A.AC=A'C'
B.BO=B'O
C.AA'⊥MN
D.AB=B'C'
【答案】【解答】解:∵△ABC与△A′B′C′关于直线MN对称,
∴AC=A′C′,AA′⊥MN,BO=B′O,故A、B、C选项正确,
AB=B′C′不一定成立,故D选项错误,所以,不一定正确的是D.
故选:D.
4.
下列图形中,不是轴对称图形的是(
)
【答案】A
5.
在平面直角坐标系中,作点A(3,4)关于x轴的对称点A′,再将点A′向左平移6个单位长度,得到点B,则点B的坐标为( )
A.(4,-3)
B.(-4,3)
C.(-3,4)
D.(-3,-4)
【答案】D [解析]
点A(3,4)关于x轴的对称点A′的坐标为(3,-4),将点A′向左平移6个单位长度,得到点B(-3,-4).
6.
如图,线段AB与A′B′(AB=A′B′)不关于直线l成轴对称的是( )
【答案】A
7.
已知,如图,点P关于OA、OB的对称点分别是P1,P2,线段P1P2分别交OA、OB于D、C,P1P2=6cm,则△PCD的周长为( )
A.3cm
B.6cm
C.12cm
D.无法确定
【答案】B
8.
如图所示的五角星是轴对称图形,它的对称轴共有( )
A.1条
B.3条
C.5条
D.无数条
【答案】C
9.
将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图4,将图4的纸片展开铺平,再得到的图案是(
)
【答案】答案为:B.
二、填空题
10.
如图所示的4组图形中,左右两个图形成轴对称的是第________组(填序号).
【答案】(3)(4)
11.
如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有
个.
【答案】答案为:4.
12.
如图是某时刻在镜子中看到准确时钟的情况,则实际时间是???????
?
【答案】答案为:4:40.??
13.
在①线段、②角、③圆、④长方形、⑤梯形、⑥三角形、⑦等边三角形中,是轴对称图形的有
(只填序号)
【答案】答案为:①②③④⑦.
14.
若点A(1﹣m,6)与B(2+n,6)关于某坐标轴对称,则m﹣n=
.
【答案】答案为:3.
15.
如图,△ABO是关于y轴对称的轴对称图形,点A的坐标为(-2,3),则点B的坐标为________.
【答案】(2,3) [解析]
∵△ABO是关于y轴对称的轴对称图形,
∴点A(-2,3)与点B关于y轴对称.∴点B的坐标为(2,3).
16.
如图所示,分别将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为E,F,G,H的四个图形,则剪前与剪后拼接的图形的对应关系是:A与________对应,B与________对应,C与________对应,D与________对应.
【答案】G E F H
[解析]
A剪开后是三个三角形,B剪开后是两个直角梯形和一个三角形,C剪开后是一个直角三角形和两个四边形,D剪开后是两个三角形和一个四边形,因而,A与G对应,B与E对应,C与F对应,D与H对应.
三、解答题
17.
如图,在平面直角坐标系中,
(1)描出A(-
4,3)B(-1,0)C(-2,3)三点.
(2)△ABC的面积是????????
(3)作出△ABC关于x轴的对称图形.
【答案】(1)如图所示;(2)3;(3)如图所示
18.
小强拿几张正方形的纸(如图4①),沿虚线对折一次得到图②,再沿虚线对折一次得到图③,然后用剪刀沿图④中不同位置的虚线剪去中心的一块,请参照例图,在后面的正方形中画出图④的纸片打开后的形状.(不写作法,保留作图痕迹)
【答案】
解:如图所示:
19.
图中的两个图形关于某条直线对称,根据图中提供的条件求出x,y的值.
【答案】
[解析]
因为两个图形关于某条直线对称,所以观察发现A和F,B和E,C和H,D和G分别是对称点,因此CD边与HG边是对应边,长度相等,∠ADC和∠FGH是对应角,大小相等.
解:x=∠ADC=360°-40°-95°-110°=115°,y=HG=3.
20.
如图,Rt△ABC的顶点A,B,C关于直线MN的对称点分别为A',B',C',其中∠A=90°,AC=8
cm,点C,B,A'在同一条直线上,且A'C=12
cm.
(1)求△A'B'C'的周长;
(2)求△A'CC'的面积.
【答案】
解:(1)∵Rt△ABC的顶点A,B,C关于直线MN的对称点分别为A',B',C',AC=8
cm,A'C=8cm,
∴AB=A'B',AC=A'C',∠A'=∠A=90°.
∴△A'B'C'的周长为A'C'+B'C'+A'B'=AC+A'C=12+8=20(cm).
(2)由(1)得A'C'=AC=8
cm,∠A'=90°,
∴△A'CC'的面积为A'C·A'C'=×12×8=48(cm2).
21.
如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(﹣3,2).请按要求分别完成下列各小题:
(1)把△ABC向下平移4个单位得到△A1B1C1,画出△A1B1C1,点A1的坐标是
;
(2)画出△ABC关于y轴对称的△A2B2C2;点C2的坐标是
;
(3)求△ABC的面积.
【答案】
解:(1)如图所示:由图可知A1(﹣3,﹣2).
故答案为:A1(﹣3,﹣2);
(2)如图所示:由图可知C2(5,3).故答案为:C2(5,3);
(3)S△ABC=2×3﹣×2×1﹣×1×2﹣×1×3=6﹣1﹣1﹣=.
22.
如图,直线AD和CE是△ABC的两条对称轴,AD和CE相交于点O,OD
与OE有什么数量关系?请说明理由.
【答案】【解答】解:OD=OE.
理由如下:∵直线AD和CE是△ABC的两条对称轴,
∴AE=BE=AB,CD=BD=BC,CE⊥AB,AD⊥BC,
而AB=BC,∴AE=CD,
在△AOE和△COD中,
∴△AOE≌△COD(AAS),
∴OD=OE.
23.
已知点A(2m+n,2),B
(1,n﹣m),当m、n分别为何值时,
(1)A、B关于x轴对称;
(2)A、B关于y轴对称.
【答案】解:
(1)∵点A(2m+n,2),B
(1,n﹣m),A、B关于x轴对称,
∴,解得;
(2)∵点A(2m+n,2),B
(1,n﹣m),A、B关于y轴对称,
∴,解得:.
第十三章
13.1
轴对称
同步练习
一、选择题
1.下列银行标志中,是轴对称图形的是(
)
A.徽商银行
B.中国建设银行
C.交通银行
D.中国银行
2.
如下图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
A.①???
?
B.②???
?
C.⑤???
?
D.⑥
3.
如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说
法不一定正确的是( )
A.AC=A'C'
B.BO=B'O
C.AA'⊥MN
D.AB=B'C'
4.
下列图形中,不是轴对称图形的是(
)
5.
在平面直角坐标系中,作点A(3,4)关于x轴的对称点A′,再将点A′向左平移6个单位长度,得到点B,则点B的坐标为( )
A.(4,-3)
B.(-4,3)
C.(-3,4)
D.(-3,-4)
6.
如图,线段AB与A′B′(AB=A′B′)不关于直线l成轴对称的是( )
7.
已知,如图,点P关于OA、OB的对称点分别是P1,P2,线段P1P2分别交OA、OB于D、C,P1P2=6cm,则△PCD的周长为( )
A.3cm
B.6cm
C.12cm
D.无法确定
8.
如图所示的五角星是轴对称图形,它的对称轴共有( )
A.1条
B.3条
C.5条
D.无数条
9.
将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图4,将图4的纸片展开铺平,再得到的图案是(
)
二、填空题
10.
如图所示的4组图形中,左右两个图形成轴对称的是第________组(填序号).
11.
如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有
个.
12.
如图是某时刻在镜子中看到准确时钟的情况,则实际时间是???????
?
13.
在①线段、②角、③圆、④长方形、⑤梯形、⑥三角形、⑦等边三角形中,是轴对称图形的有
(只填序号)
14.
若点A(1﹣m,6)与B(2+n,6)关于某坐标轴对称,则m﹣n=
.
15.
如图,△ABO是关于y轴对称的轴对称图形,点A的坐标为(-2,3),则点B的坐标为________.
16.
如图所示,分别将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为E,F,G,H的四个图形,则剪前与剪后拼接的图形的对应关系是:A与________对应,B与________对应,C与________对应,D与________对应.
三、解答题
17.
如图,在平面直角坐标系中,
(1)描出A(-
4,3)B(-1,0)C(-2,3)三点.
(2)△ABC的面积是????????
(3)作出△ABC关于x轴的对称图形.
18.
小强拿几张正方形的纸(如图4①),沿虚线对折一次得到图②,再沿虚线对折一次得到图③,然后用剪刀沿图④中不同位置的虚线剪去中心的一块,请参照例图,在后面的正方形中画出图④的纸片打开后的形状.(不写作法,保留作图痕迹)
19.
图中的两个图形关于某条直线对称,根据图中提供的条件求出x,y的值.
20.
如图,Rt△ABC的顶点A,B,C关于直线MN的对称点分别为A',B',C',其中∠A=90°,AC=8
cm,点C,B,A'在同一条直线上,且A'C=12
cm.
(1)求△A'B'C'的周长;
(2)求△A'CC'的面积.
21.
如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(﹣3,2).请按要求分别完成下列各小题:
(1)把△ABC向下平移4个单位得到△A1B1C1,画出△A1B1C1,点A1的坐标是
;
(2)画出△ABC关于y轴对称的△A2B2C2;点C2的坐标是
;
(3)求△ABC的面积.
22.
如图,直线AD和CE是△ABC的两条对称轴,AD和CE相交于点O,OD
与OE有什么数量关系?请说明理由.
23.
已知点A(2m+n,2),B
(1,n﹣m),当m、n分别为何值时,
(1)A、B关于x轴对称;
(2)A、B关于y轴对称.
人教版数学八年级上册
第十三章
13.1
轴对称
同步练习--参考答案
一、选择题
1.下列银行标志中,是轴对称图形的是(
)
A.徽商银行
B.中国建设银行
C.交通银行
D.中国银行
【答案】D
2.
如下图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
A.①???
?
B.②???
?
C.⑤???
?
D.⑥
【答案】答案为:B
3.
如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说
法不一定正确的是( )
A.AC=A'C'
B.BO=B'O
C.AA'⊥MN
D.AB=B'C'
【答案】【解答】解:∵△ABC与△A′B′C′关于直线MN对称,
∴AC=A′C′,AA′⊥MN,BO=B′O,故A、B、C选项正确,
AB=B′C′不一定成立,故D选项错误,所以,不一定正确的是D.
故选:D.
4.
下列图形中,不是轴对称图形的是(
)
【答案】A
5.
在平面直角坐标系中,作点A(3,4)关于x轴的对称点A′,再将点A′向左平移6个单位长度,得到点B,则点B的坐标为( )
A.(4,-3)
B.(-4,3)
C.(-3,4)
D.(-3,-4)
【答案】D [解析]
点A(3,4)关于x轴的对称点A′的坐标为(3,-4),将点A′向左平移6个单位长度,得到点B(-3,-4).
6.
如图,线段AB与A′B′(AB=A′B′)不关于直线l成轴对称的是( )
【答案】A
7.
已知,如图,点P关于OA、OB的对称点分别是P1,P2,线段P1P2分别交OA、OB于D、C,P1P2=6cm,则△PCD的周长为( )
A.3cm
B.6cm
C.12cm
D.无法确定
【答案】B
8.
如图所示的五角星是轴对称图形,它的对称轴共有( )
A.1条
B.3条
C.5条
D.无数条
【答案】C
9.
将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图4,将图4的纸片展开铺平,再得到的图案是(
)
【答案】答案为:B.
二、填空题
10.
如图所示的4组图形中,左右两个图形成轴对称的是第________组(填序号).
【答案】(3)(4)
11.
如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有
个.
【答案】答案为:4.
12.
如图是某时刻在镜子中看到准确时钟的情况,则实际时间是???????
?
【答案】答案为:4:40.??
13.
在①线段、②角、③圆、④长方形、⑤梯形、⑥三角形、⑦等边三角形中,是轴对称图形的有
(只填序号)
【答案】答案为:①②③④⑦.
14.
若点A(1﹣m,6)与B(2+n,6)关于某坐标轴对称,则m﹣n=
.
【答案】答案为:3.
15.
如图,△ABO是关于y轴对称的轴对称图形,点A的坐标为(-2,3),则点B的坐标为________.
【答案】(2,3) [解析]
∵△ABO是关于y轴对称的轴对称图形,
∴点A(-2,3)与点B关于y轴对称.∴点B的坐标为(2,3).
16.
如图所示,分别将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为E,F,G,H的四个图形,则剪前与剪后拼接的图形的对应关系是:A与________对应,B与________对应,C与________对应,D与________对应.
【答案】G E F H
[解析]
A剪开后是三个三角形,B剪开后是两个直角梯形和一个三角形,C剪开后是一个直角三角形和两个四边形,D剪开后是两个三角形和一个四边形,因而,A与G对应,B与E对应,C与F对应,D与H对应.
三、解答题
17.
如图,在平面直角坐标系中,
(1)描出A(-
4,3)B(-1,0)C(-2,3)三点.
(2)△ABC的面积是????????
(3)作出△ABC关于x轴的对称图形.
【答案】(1)如图所示;(2)3;(3)如图所示
18.
小强拿几张正方形的纸(如图4①),沿虚线对折一次得到图②,再沿虚线对折一次得到图③,然后用剪刀沿图④中不同位置的虚线剪去中心的一块,请参照例图,在后面的正方形中画出图④的纸片打开后的形状.(不写作法,保留作图痕迹)
【答案】
解:如图所示:
19.
图中的两个图形关于某条直线对称,根据图中提供的条件求出x,y的值.
【答案】
[解析]
因为两个图形关于某条直线对称,所以观察发现A和F,B和E,C和H,D和G分别是对称点,因此CD边与HG边是对应边,长度相等,∠ADC和∠FGH是对应角,大小相等.
解:x=∠ADC=360°-40°-95°-110°=115°,y=HG=3.
20.
如图,Rt△ABC的顶点A,B,C关于直线MN的对称点分别为A',B',C',其中∠A=90°,AC=8
cm,点C,B,A'在同一条直线上,且A'C=12
cm.
(1)求△A'B'C'的周长;
(2)求△A'CC'的面积.
【答案】
解:(1)∵Rt△ABC的顶点A,B,C关于直线MN的对称点分别为A',B',C',AC=8
cm,A'C=8cm,
∴AB=A'B',AC=A'C',∠A'=∠A=90°.
∴△A'B'C'的周长为A'C'+B'C'+A'B'=AC+A'C=12+8=20(cm).
(2)由(1)得A'C'=AC=8
cm,∠A'=90°,
∴△A'CC'的面积为A'C·A'C'=×12×8=48(cm2).
21.
如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(﹣3,2).请按要求分别完成下列各小题:
(1)把△ABC向下平移4个单位得到△A1B1C1,画出△A1B1C1,点A1的坐标是
;
(2)画出△ABC关于y轴对称的△A2B2C2;点C2的坐标是
;
(3)求△ABC的面积.
【答案】
解:(1)如图所示:由图可知A1(﹣3,﹣2).
故答案为:A1(﹣3,﹣2);
(2)如图所示:由图可知C2(5,3).故答案为:C2(5,3);
(3)S△ABC=2×3﹣×2×1﹣×1×2﹣×1×3=6﹣1﹣1﹣=.
22.
如图,直线AD和CE是△ABC的两条对称轴,AD和CE相交于点O,OD
与OE有什么数量关系?请说明理由.
【答案】【解答】解:OD=OE.
理由如下:∵直线AD和CE是△ABC的两条对称轴,
∴AE=BE=AB,CD=BD=BC,CE⊥AB,AD⊥BC,
而AB=BC,∴AE=CD,
在△AOE和△COD中,
∴△AOE≌△COD(AAS),
∴OD=OE.
23.
已知点A(2m+n,2),B
(1,n﹣m),当m、n分别为何值时,
(1)A、B关于x轴对称;
(2)A、B关于y轴对称.
【答案】解:
(1)∵点A(2m+n,2),B
(1,n﹣m),A、B关于x轴对称,
∴,解得;
(2)∵点A(2m+n,2),B
(1,n﹣m),A、B关于y轴对称,
∴,解得:.
