青岛版数学八年级上册第三章分式章节测试(Word版 含解析)
文档属性
| 名称 | 青岛版数学八年级上册第三章分式章节测试(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 65.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 10:43:52 | ||
图片预览




文档简介
青岛版八年级第三章分式章节测试
一、选择题(本大题共12小题,共36.0分)
下列四个分式中,是最简分式的是
A.
B.
C.
D.
已知,则的值等于
A.
1
B.
0
C.
D.
若分式的值为0,则x的值为
A.
B.
0
C.
1
D.
如图,AD是的中线,E是AD中点,BE的延长线与AC交于点F,则AF:AC等于?
?
A.
1:2
B.
2:3
C.
1:3
D.
2:5
将分式中的x、y的值同时扩大3倍,则分式的值
A.
扩大3倍
B.
缩小到原来的
C.
保持不变
D.
扩大9倍
如果解关于x的分式方程时出现增根,那么m的值为
A.
B.
2
C.
4
D.
若分式的值为零,则x的值是
A.
1
B.
C.
D.
2
解分式方程,去分母得
A.
B.
C.
D.
若x、y的值均扩大为原来的2倍,则下列分式的值保持不变的是
A.
B.
C.
D.
如图,是等腰三角形,,?点D在AB边上,点E在CB的延长线上,已知,,连接ED并延长交AC于点F,则线段AF的长为
A.
B.
C.
D.
1
使分式有意义的x的取值范围是
A.
B.
C.
D.
若分式,则x的值是?
A.
3或
B.
C.
3
D.
9
二、判断题(本大题共5小题,共15.0分)
一个数除以?,相当于把这个数扩大到原来4倍。?
A.
T
B.
F
行同一段路,甲用小时,乙用小时,甲、乙速度之比是。??
???
A.
正确
B.
错误
一个数除以,相当于把这个数扩大到原来的10倍。?????
A.
正确
B.
错误
圆的半径和它的面积不成比例.____
A.
T
B.
F
甲数的等于乙数的,则甲乙两数之比为2:3。?
A.
正确
B.
错误
三、计算题(本大题共2小题,共12.0分)
???????????
.
??????
.
先化简,再求值:,其中.
四、解答题(本大题共6小题,共48.0分)
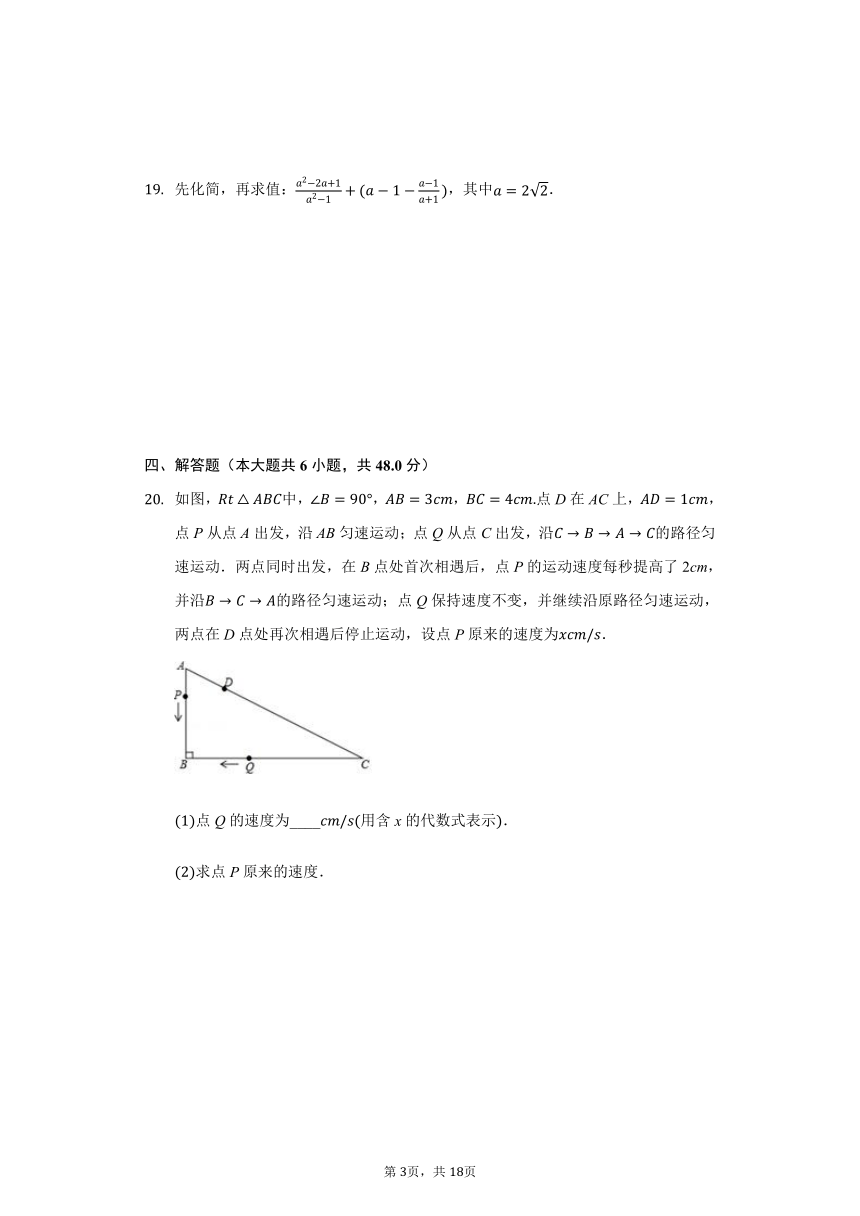
如图,中,,,点D在AC上,,点P从点A出发,沿AB匀速运动;点Q从点C出发,沿的路径匀速运动.两点同时出发,在B点处首次相遇后,点P的运动速度每秒提高了2cm,并沿的路径匀速运动;点Q保持速度不变,并继续沿原路径匀速运动,两点在D点处再次相遇后停止运动,设点P原来的速度为.
点Q的速度为____用含x的代数式表示.
求点P原来的速度.
某公司购买了一批A、B型芯片,其中A型芯片的单价比B型芯片的单价少9元,已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等.
求该公司购买的A、B型芯片的单价各是多少元?
若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条A型芯片?
为厉行节能减排,倡导绿色出行,今年3月以来,“共享单车”俗称“小黄车”登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
某书店老板去图书批发市场购买某种图书,第一次用1200元购书若干本,并按该书定价7元出售,很快售完,由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了,他用1500元所购该书的数量比第一次多10本,当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.
第一次购书的进价是多少元?
试问该老板这两次售书总体上是赔钱了,还是赚钱了不考虑其他因素?若赔钱,赔多少;若赚钱,赚多少?
某玩具店用2000元购进一批玩具,面市后,供不应求,于是店主又购进同样的玩具,所购的数量是第一批数量的3倍,但每件进价贵了4元,结果购进第二批玩具共用了6300元.若两批玩具的售价都是每件120元,且两批玩具全部售完.
第一次购进了多少件玩具?
求该玩具店销售这两批玩具共盈利多少元?
观察以下等式:
第1个等式:,
第2个等式:,
第3个等式:,
第4个等式:,
第5个等式:,
按照以上规律,解决下列问题:
写出第6个等式:______;
写出你猜想的第n个等式:______用含n的等式表示,并证明.
答案和解析
1.【答案】A
【解析】
【分析】
本题考查最简分式的概念,涉及因式分解,分式的基本性质,本题属于基础题型.
分子分母没有公因式即可为最简分式.
【解答】
解:A.,最简分式;
B.原式,故B不是最简分式;
C.原式,故C不是最简分式;
D.原式,故D不是最简分式.
故选A.
2.【答案】C
【解析】解:由,得
?
,
则,,
.
故选:C.
把所给等式整理为2个完全平方式的和为0的形式,得到m,n的值,代入求值即可.
考查分式的化简求值,把所给等式整理为2个完全平方式的和为0的形式是解决本题的突破点;用到的知识点为:2个完全平方式的和为0,这2个完全平方式的底数为0.
3.【答案】A
【解析】
【分析】
此题主要考查了分式的值为零,正确把握相关定义是解题关键.直接利用分式的值为零则分子为零,分母不等于零,进而得出答案.
【解答】
解:分式的值为0,
,,
解得:.
故选A.
4.【答案】C
【解析】
【分析】
本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.
作交AC于H,根据平行线分线段成比例定理得到,得到答案.
【解答】
解:作交AC于H,
,AD是的中线,
,
,E是AD中点,
,
,
::3,
故选C.
5.【答案】A
【解析】
【分析】
本题考查分式的基本性质,属于基础题.
根据x、y的值同时扩大3倍后求出分式的值,和原来比较求出结果.
【解答】
解:中的x、y的值同时扩大3倍,.
所以扩大了3倍.
故选A.
6.【答案】D
【解析】
【分析】
本题主要考查分式方程解法增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母,确定可能的增根;然后代入化为整式方程的方程求解,即可得到正确的答案.
【解答】
解:,
去分母,方程两边同时乘以,得:
,
由分母可知,分式方程的增根是2,
当时,,
,
故选D.
7.【答案】A
【解析】
【分析】
此题主要考查了分式的值为零,正确把握相关定义是解题关键,直接利用分式的值为零,则分子为零,分母不为零,进而得出答案.
【解答】
解:分式的值为零,
,,
解得:.
故选:A.
8.【答案】A
【解析】
【分析】
此题主要考查了解分式方程的去分母步骤.
分式方程变形后,两边乘以最简公分母得到结果,即可作出判断.
【解答】
解:分式方程整理得:,
去分母得:,
故选A.
9.【答案】A
【解析】
【分析】
本题考查的是分式的基本性质,即分子分母同乘以一个不为0的数,分式的值不变.此题比较简单,但计算时一定要细心据分式的基本性质,x,y的值均扩大为原来的2倍,求出每个式子的结果,看结果等于原式的即可.
【解答】
解:根据分式的基本性质,可知若x,y的值均扩大为原来的2倍,
A.,故正确;
B.,故错误;
C.,故错误;
D.,故错误.
故选A.
10.【答案】B
【解析】
【分析】
取CF的中点G,连接BG,证出BG是的中位线,由三角形中位线定理得出,得出比例式,因此,,得出,即可得出AF的长.
本题考查了平行线分线段成比例定理、三角形中位线定理;熟练掌握平行线分线段成比例定理,由三角形中位线定理得出是解决问题的关键.
【解答】
解:取CF的中点G,连接BG,如图所示:
,,
点B为EC的中点,
是的中位线,
,
,
,
,
,
;
故选:B.
11.【答案】B
【解析】
【分析】
此题主要考查了分式有意义的条件,正确记忆相关定义是解题关键;直接利用分式有意义则其分母不为零,进而得出答案.
【解答】
解:使分式有意义,
,
解得:.
故选B.
12.【答案】B
【解析】
【分析】
本题主要考查分式的值为0的条件,多项式的因式分解,关键在于根据题意确定x的值.
先对分式的分子和分母进行因式分解,推出,根据题意可推出,根据分式有意义检验,即可得解.
【解答】
解:,
,
,
或,
时,,分式无意义,
.
故选B.
13.【答案】F
【解析】
【分析】
本题主要考查分式的定义和乘法,属于基础题.
【解答】
解:一个数除以?,相当于把这个数乘以4,即扩大到原来4倍,但是要排除0.
故答案为F.
14.【答案】A
【解析】
【分析】
本题的关健是先确定路程为“1”,然后再求各自的速度.本题可以设路程为“1”,路程时间速度,从而根据他们所用时间求出各自的速度,就能求出速度比了.
【解答】
解:设路程为“1”,则甲乙的速度比为:
::4,
故答案为A.
15.【答案】B
【解析】
【分析】
本题主要考查分式的定义和乘法,属于基础题.
【解答】
解:一个数除以?,相当于把这个数乘以10,即扩大到原来10倍,但是要排除0.
故答案为B.
16.【答案】A
【解析】
【分析】
此题属于根据正、反比例的意义,判断两种相关联的量成不成比例,成什么比例,就看这两种量中相对应的两个数是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例.圆的半径和它的面积虽然相关联,面积也随着半径的变化而变化,变化方法相同,但是面积:半径圆周率半径,半径是变量,所以圆周率半径就不一定,是圆的半径和它的面积的比值不一定,所以圆的半径和它的面积不成比例.
【解答】
解:因为面积:半径圆周率半径,半径是变量,所以圆周率半径就不一定,
是圆的半径和它的面积的比值不一定,所以圆的半径和它的面积不成比例.
故选A.
17.【答案】A
【解析】
【分析】
关键是根据题意写出数量关系等式,再灵活利用比例的基本性质解决问题.根据“甲数的等于乙数的,知道甲数等于乙数,再逆用比例的基本性质乘积式化为比例式解决问题.
【解答】
解:甲数等于乙数,
所以甲数:乙数::3,
所以题干的说法是正确的;
故选A.
18.【答案】解:原式
;
原式
;
原式
;
原式
.
【解析】本题考查了分式的混合运算,需掌握的知识点:分式的混合运算的顺序和法则,分式的约分、通分以及因式分解;熟练掌握分式的混合运算顺序和因式分解是解决问题的关键.
首先通分计算括号里面,进而根据分式的加减乘除混合运算顺序进行约分计算即可;
根据分式的加减乘除混合运算顺序进行计算,注意进行因式分解和约分;
首先通分计算括号里面再根据分式的加减乘除混合运算顺序进行计算,注意进行因式分解和约分;
根据分式的加减法法则进行计算,注意通分.
19.【答案】解:
当时
原式
【解析】首先化简,然后把代入化简后的算式,求出算式的值是多少即可.
此题主要考查了分式的化简求值问题,要熟练掌握,注意先把分式化简后,再把分式中未知数对应的值代入求出分式的值.
20.【答案】解:;
,
,
在B点处首次相遇后,点P的运动速度为,
由题意得,
解得:,
答:点P原来的速度为.
【解析】
【分析】
本题考查了分式方程的应用,勾股定理,正确的理解题意是解题的关键;设点Q的速度为,根据题意列方程即可得到结论;根据勾股定理得到,求得,列方程即可得到结论.
【解答】
解:设点Q的速度为,
由题意得,
,
故答案为;
见答案.
21.【答案】解:设B型芯片的单价为x元条,则A型芯片的单价为元条,
根据题意得:,
解得:,
经检验,是原方程的解,且符合题意,
.
答:A型芯片的单价为26元条,B型芯片的单价为35元条.
设购买a条A型芯片,则购买条B型芯片,
根据题意得:,
解得:.
答:购买了80条A型芯片.
【解析】本题考查了分式方程的应用以及一元一次方程的应用,解题的关键是:找准等量关系,正确列出分式方程;找准等量关系,正确列出一元一次方程.
设B型芯片的单价为x元条,则A型芯片的单价为元条,根据数量总价单价结合用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等,即可得出关于x的分式方程,解之经检验后即可得出结论;
设购买a条A型芯片,则购买条B型芯片,根据总价单价数量,即可得出关于a的一元一次方程,解之即可得出结论.
22.【答案】解:问题1
设A型车的成本单价为x元,则B型车的成本单价为元,依题意得
,
解得,
,
答:A、B两型自行车的单价分别是70元和80元;
问题2
由题可得,,
解得,
经检验:是所列方程的解,且符合题意,
故a的值为15.
【解析】本题主要考查了一元一次方程以及分式方程的应用,解题时注意:列分式方程解应用题一定要审清题意,找相等关系是着眼点,要学会分析题意,提高理解能力.
问题1:设A型车的成本单价为x元,则B型车的成本单价为元,根据成本共计7500元,列方程求解即可;
问题2:根据两个街区共有15万人,列出分式方程进行求解并检验即可.
23.【答案】解:设第一次购书的单价为x元,根据题意得:
.
解得:.
经检验,是原方程的解,且符合题意,
答:第一次购书的进价是5元;
第一次购书为本,
第二次购书为本,
第一次赚钱为元,
第二次赚钱为元,
所以两次共赚钱元,
答:该老板两次售书总体上是赚钱了,共赚了520元.
【解析】此题考查了分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.
设第一次购书的单价为x元,根据题意列出方程,求出x的值即可得出答案;
根据先求出第一次和第二次购书数目,再根据卖书数目实际售价当次进价求出两次赚的钱数,再分别相加即可得出答案.
24.【答案】解:设第一次购进了x件玩具,则第二次购进了3x件玩具,
根据题意得:,
解得:,
经检验,是原分式方程的解.
答:第一次购进了25件玩具.
元.
答:该玩具店销售这两批玩具共盈利3700元.
【解析】本题考查了分式方程的应用,解题的关键是:根据单价总价数量,结合第二批的进价比第一批每件贵了4元,列出关于x的分式方程;根据利润销售收入成本,列式计算.
设第一次购进了x件玩具,则第二次购进了3x件玩具,根据单价总价数量,结合第二批的进价比第一批每件贵了4元,即可得出关于x的分式方程,解之经检验后即可得出结论;
根据利润销售收入成本,即可算出该玩具店销售这两批玩具共盈利多少元.
25.【答案】;
.
证明:,
等式成立.
【解析】解:根据已知规律,第6个等式的分母分别为6和7,分子分别为1和5,
故应填:;
见答案.
依此观察每个等式,发现规律,依据规律求解即可.
本题是规律探究题,同时考查分式的化简.解答过程中,要注意各式中相同位置数字的变化规律,并将其用代数式表示出来.
第2页,共2页
第1页,共1页
一、选择题(本大题共12小题,共36.0分)
下列四个分式中,是最简分式的是
A.
B.
C.
D.
已知,则的值等于
A.
1
B.
0
C.
D.
若分式的值为0,则x的值为
A.
B.
0
C.
1
D.
如图,AD是的中线,E是AD中点,BE的延长线与AC交于点F,则AF:AC等于?
?
A.
1:2
B.
2:3
C.
1:3
D.
2:5
将分式中的x、y的值同时扩大3倍,则分式的值
A.
扩大3倍
B.
缩小到原来的
C.
保持不变
D.
扩大9倍
如果解关于x的分式方程时出现增根,那么m的值为
A.
B.
2
C.
4
D.
若分式的值为零,则x的值是
A.
1
B.
C.
D.
2
解分式方程,去分母得
A.
B.
C.
D.
若x、y的值均扩大为原来的2倍,则下列分式的值保持不变的是
A.
B.
C.
D.
如图,是等腰三角形,,?点D在AB边上,点E在CB的延长线上,已知,,连接ED并延长交AC于点F,则线段AF的长为
A.
B.
C.
D.
1
使分式有意义的x的取值范围是
A.
B.
C.
D.
若分式,则x的值是?
A.
3或
B.
C.
3
D.
9
二、判断题(本大题共5小题,共15.0分)
一个数除以?,相当于把这个数扩大到原来4倍。?
A.
T
B.
F
行同一段路,甲用小时,乙用小时,甲、乙速度之比是。??
???
A.
正确
B.
错误
一个数除以,相当于把这个数扩大到原来的10倍。?????
A.
正确
B.
错误
圆的半径和它的面积不成比例.____
A.
T
B.
F
甲数的等于乙数的,则甲乙两数之比为2:3。?
A.
正确
B.
错误
三、计算题(本大题共2小题,共12.0分)
???????????
.
??????
.
先化简,再求值:,其中.
四、解答题(本大题共6小题,共48.0分)
如图,中,,,点D在AC上,,点P从点A出发,沿AB匀速运动;点Q从点C出发,沿的路径匀速运动.两点同时出发,在B点处首次相遇后,点P的运动速度每秒提高了2cm,并沿的路径匀速运动;点Q保持速度不变,并继续沿原路径匀速运动,两点在D点处再次相遇后停止运动,设点P原来的速度为.
点Q的速度为____用含x的代数式表示.
求点P原来的速度.
某公司购买了一批A、B型芯片,其中A型芯片的单价比B型芯片的单价少9元,已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等.
求该公司购买的A、B型芯片的单价各是多少元?
若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条A型芯片?
为厉行节能减排,倡导绿色出行,今年3月以来,“共享单车”俗称“小黄车”登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
某书店老板去图书批发市场购买某种图书,第一次用1200元购书若干本,并按该书定价7元出售,很快售完,由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了,他用1500元所购该书的数量比第一次多10本,当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.
第一次购书的进价是多少元?
试问该老板这两次售书总体上是赔钱了,还是赚钱了不考虑其他因素?若赔钱,赔多少;若赚钱,赚多少?
某玩具店用2000元购进一批玩具,面市后,供不应求,于是店主又购进同样的玩具,所购的数量是第一批数量的3倍,但每件进价贵了4元,结果购进第二批玩具共用了6300元.若两批玩具的售价都是每件120元,且两批玩具全部售完.
第一次购进了多少件玩具?
求该玩具店销售这两批玩具共盈利多少元?
观察以下等式:
第1个等式:,
第2个等式:,
第3个等式:,
第4个等式:,
第5个等式:,
按照以上规律,解决下列问题:
写出第6个等式:______;
写出你猜想的第n个等式:______用含n的等式表示,并证明.
答案和解析
1.【答案】A
【解析】
【分析】
本题考查最简分式的概念,涉及因式分解,分式的基本性质,本题属于基础题型.
分子分母没有公因式即可为最简分式.
【解答】
解:A.,最简分式;
B.原式,故B不是最简分式;
C.原式,故C不是最简分式;
D.原式,故D不是最简分式.
故选A.
2.【答案】C
【解析】解:由,得
?
,
则,,
.
故选:C.
把所给等式整理为2个完全平方式的和为0的形式,得到m,n的值,代入求值即可.
考查分式的化简求值,把所给等式整理为2个完全平方式的和为0的形式是解决本题的突破点;用到的知识点为:2个完全平方式的和为0,这2个完全平方式的底数为0.
3.【答案】A
【解析】
【分析】
此题主要考查了分式的值为零,正确把握相关定义是解题关键.直接利用分式的值为零则分子为零,分母不等于零,进而得出答案.
【解答】
解:分式的值为0,
,,
解得:.
故选A.
4.【答案】C
【解析】
【分析】
本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.
作交AC于H,根据平行线分线段成比例定理得到,得到答案.
【解答】
解:作交AC于H,
,AD是的中线,
,
,E是AD中点,
,
,
::3,
故选C.
5.【答案】A
【解析】
【分析】
本题考查分式的基本性质,属于基础题.
根据x、y的值同时扩大3倍后求出分式的值,和原来比较求出结果.
【解答】
解:中的x、y的值同时扩大3倍,.
所以扩大了3倍.
故选A.
6.【答案】D
【解析】
【分析】
本题主要考查分式方程解法增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母,确定可能的增根;然后代入化为整式方程的方程求解,即可得到正确的答案.
【解答】
解:,
去分母,方程两边同时乘以,得:
,
由分母可知,分式方程的增根是2,
当时,,
,
故选D.
7.【答案】A
【解析】
【分析】
此题主要考查了分式的值为零,正确把握相关定义是解题关键,直接利用分式的值为零,则分子为零,分母不为零,进而得出答案.
【解答】
解:分式的值为零,
,,
解得:.
故选:A.
8.【答案】A
【解析】
【分析】
此题主要考查了解分式方程的去分母步骤.
分式方程变形后,两边乘以最简公分母得到结果,即可作出判断.
【解答】
解:分式方程整理得:,
去分母得:,
故选A.
9.【答案】A
【解析】
【分析】
本题考查的是分式的基本性质,即分子分母同乘以一个不为0的数,分式的值不变.此题比较简单,但计算时一定要细心据分式的基本性质,x,y的值均扩大为原来的2倍,求出每个式子的结果,看结果等于原式的即可.
【解答】
解:根据分式的基本性质,可知若x,y的值均扩大为原来的2倍,
A.,故正确;
B.,故错误;
C.,故错误;
D.,故错误.
故选A.
10.【答案】B
【解析】
【分析】
取CF的中点G,连接BG,证出BG是的中位线,由三角形中位线定理得出,得出比例式,因此,,得出,即可得出AF的长.
本题考查了平行线分线段成比例定理、三角形中位线定理;熟练掌握平行线分线段成比例定理,由三角形中位线定理得出是解决问题的关键.
【解答】
解:取CF的中点G,连接BG,如图所示:
,,
点B为EC的中点,
是的中位线,
,
,
,
,
,
;
故选:B.
11.【答案】B
【解析】
【分析】
此题主要考查了分式有意义的条件,正确记忆相关定义是解题关键;直接利用分式有意义则其分母不为零,进而得出答案.
【解答】
解:使分式有意义,
,
解得:.
故选B.
12.【答案】B
【解析】
【分析】
本题主要考查分式的值为0的条件,多项式的因式分解,关键在于根据题意确定x的值.
先对分式的分子和分母进行因式分解,推出,根据题意可推出,根据分式有意义检验,即可得解.
【解答】
解:,
,
,
或,
时,,分式无意义,
.
故选B.
13.【答案】F
【解析】
【分析】
本题主要考查分式的定义和乘法,属于基础题.
【解答】
解:一个数除以?,相当于把这个数乘以4,即扩大到原来4倍,但是要排除0.
故答案为F.
14.【答案】A
【解析】
【分析】
本题的关健是先确定路程为“1”,然后再求各自的速度.本题可以设路程为“1”,路程时间速度,从而根据他们所用时间求出各自的速度,就能求出速度比了.
【解答】
解:设路程为“1”,则甲乙的速度比为:
::4,
故答案为A.
15.【答案】B
【解析】
【分析】
本题主要考查分式的定义和乘法,属于基础题.
【解答】
解:一个数除以?,相当于把这个数乘以10,即扩大到原来10倍,但是要排除0.
故答案为B.
16.【答案】A
【解析】
【分析】
此题属于根据正、反比例的意义,判断两种相关联的量成不成比例,成什么比例,就看这两种量中相对应的两个数是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例.圆的半径和它的面积虽然相关联,面积也随着半径的变化而变化,变化方法相同,但是面积:半径圆周率半径,半径是变量,所以圆周率半径就不一定,是圆的半径和它的面积的比值不一定,所以圆的半径和它的面积不成比例.
【解答】
解:因为面积:半径圆周率半径,半径是变量,所以圆周率半径就不一定,
是圆的半径和它的面积的比值不一定,所以圆的半径和它的面积不成比例.
故选A.
17.【答案】A
【解析】
【分析】
关键是根据题意写出数量关系等式,再灵活利用比例的基本性质解决问题.根据“甲数的等于乙数的,知道甲数等于乙数,再逆用比例的基本性质乘积式化为比例式解决问题.
【解答】
解:甲数等于乙数,
所以甲数:乙数::3,
所以题干的说法是正确的;
故选A.
18.【答案】解:原式
;
原式
;
原式
;
原式
.
【解析】本题考查了分式的混合运算,需掌握的知识点:分式的混合运算的顺序和法则,分式的约分、通分以及因式分解;熟练掌握分式的混合运算顺序和因式分解是解决问题的关键.
首先通分计算括号里面,进而根据分式的加减乘除混合运算顺序进行约分计算即可;
根据分式的加减乘除混合运算顺序进行计算,注意进行因式分解和约分;
首先通分计算括号里面再根据分式的加减乘除混合运算顺序进行计算,注意进行因式分解和约分;
根据分式的加减法法则进行计算,注意通分.
19.【答案】解:
当时
原式
【解析】首先化简,然后把代入化简后的算式,求出算式的值是多少即可.
此题主要考查了分式的化简求值问题,要熟练掌握,注意先把分式化简后,再把分式中未知数对应的值代入求出分式的值.
20.【答案】解:;
,
,
在B点处首次相遇后,点P的运动速度为,
由题意得,
解得:,
答:点P原来的速度为.
【解析】
【分析】
本题考查了分式方程的应用,勾股定理,正确的理解题意是解题的关键;设点Q的速度为,根据题意列方程即可得到结论;根据勾股定理得到,求得,列方程即可得到结论.
【解答】
解:设点Q的速度为,
由题意得,
,
故答案为;
见答案.
21.【答案】解:设B型芯片的单价为x元条,则A型芯片的单价为元条,
根据题意得:,
解得:,
经检验,是原方程的解,且符合题意,
.
答:A型芯片的单价为26元条,B型芯片的单价为35元条.
设购买a条A型芯片,则购买条B型芯片,
根据题意得:,
解得:.
答:购买了80条A型芯片.
【解析】本题考查了分式方程的应用以及一元一次方程的应用,解题的关键是:找准等量关系,正确列出分式方程;找准等量关系,正确列出一元一次方程.
设B型芯片的单价为x元条,则A型芯片的单价为元条,根据数量总价单价结合用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等,即可得出关于x的分式方程,解之经检验后即可得出结论;
设购买a条A型芯片,则购买条B型芯片,根据总价单价数量,即可得出关于a的一元一次方程,解之即可得出结论.
22.【答案】解:问题1
设A型车的成本单价为x元,则B型车的成本单价为元,依题意得
,
解得,
,
答:A、B两型自行车的单价分别是70元和80元;
问题2
由题可得,,
解得,
经检验:是所列方程的解,且符合题意,
故a的值为15.
【解析】本题主要考查了一元一次方程以及分式方程的应用,解题时注意:列分式方程解应用题一定要审清题意,找相等关系是着眼点,要学会分析题意,提高理解能力.
问题1:设A型车的成本单价为x元,则B型车的成本单价为元,根据成本共计7500元,列方程求解即可;
问题2:根据两个街区共有15万人,列出分式方程进行求解并检验即可.
23.【答案】解:设第一次购书的单价为x元,根据题意得:
.
解得:.
经检验,是原方程的解,且符合题意,
答:第一次购书的进价是5元;
第一次购书为本,
第二次购书为本,
第一次赚钱为元,
第二次赚钱为元,
所以两次共赚钱元,
答:该老板两次售书总体上是赚钱了,共赚了520元.
【解析】此题考查了分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.
设第一次购书的单价为x元,根据题意列出方程,求出x的值即可得出答案;
根据先求出第一次和第二次购书数目,再根据卖书数目实际售价当次进价求出两次赚的钱数,再分别相加即可得出答案.
24.【答案】解:设第一次购进了x件玩具,则第二次购进了3x件玩具,
根据题意得:,
解得:,
经检验,是原分式方程的解.
答:第一次购进了25件玩具.
元.
答:该玩具店销售这两批玩具共盈利3700元.
【解析】本题考查了分式方程的应用,解题的关键是:根据单价总价数量,结合第二批的进价比第一批每件贵了4元,列出关于x的分式方程;根据利润销售收入成本,列式计算.
设第一次购进了x件玩具,则第二次购进了3x件玩具,根据单价总价数量,结合第二批的进价比第一批每件贵了4元,即可得出关于x的分式方程,解之经检验后即可得出结论;
根据利润销售收入成本,即可算出该玩具店销售这两批玩具共盈利多少元.
25.【答案】;
.
证明:,
等式成立.
【解析】解:根据已知规律,第6个等式的分母分别为6和7,分子分别为1和5,
故应填:;
见答案.
依此观察每个等式,发现规律,依据规律求解即可.
本题是规律探究题,同时考查分式的化简.解答过程中,要注意各式中相同位置数字的变化规律,并将其用代数式表示出来.
第2页,共2页
第1页,共1页
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
