人教版 九年级上册数学 24.1 圆的有关性质 同步训练(word版 含答案)
文档属性
| 名称 | 人教版 九年级上册数学 24.1 圆的有关性质 同步训练(word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 707.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 00:00:00 | ||
图片预览



文档简介
人教版
九年级数学
24.1
圆的有关性质
同步训练
一、选择题(本大题共10道小题)
1.
2018·衢州
如图,点A,B,C在⊙O上,∠ACB=35°,则∠AOB的度数是( )
A.75°
B.70°
C.65°
D.35°
2.
如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论正确的是( )
A.OE=BE
B.=
C.△BOC是等边三角形
D.四边形ODBC是菱形
3.
如图,四边形ABCD是圆内接四边形,E是BC延长线上一点.若∠BAD=105°,则∠DCE的度数为
( )
A.115°
B.105°
C.100°
D.95°
4.
2019·梧州
如图,在半径为的⊙O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是( )
A.2
B.2
C.2
D.4
5.
(2019?广元)如图,AB,AC分别是⊙O的直径和弦,于点D,连接BD,BC,且,,则BD的长为
A.
B.4
C.
D.4.8
6.
如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC,若∠BAC与∠BOC互补,则弦BC的长为( )
A.
3
B.
4
C.
5
D.
6
7.
如图,△ABC的内心为I,连接AI并延长交△ABC的外接圆于点D,则线段DI与DB的关系是( )
A.DI=DB
B.DI>DB
C.DI<DB
D.不确定
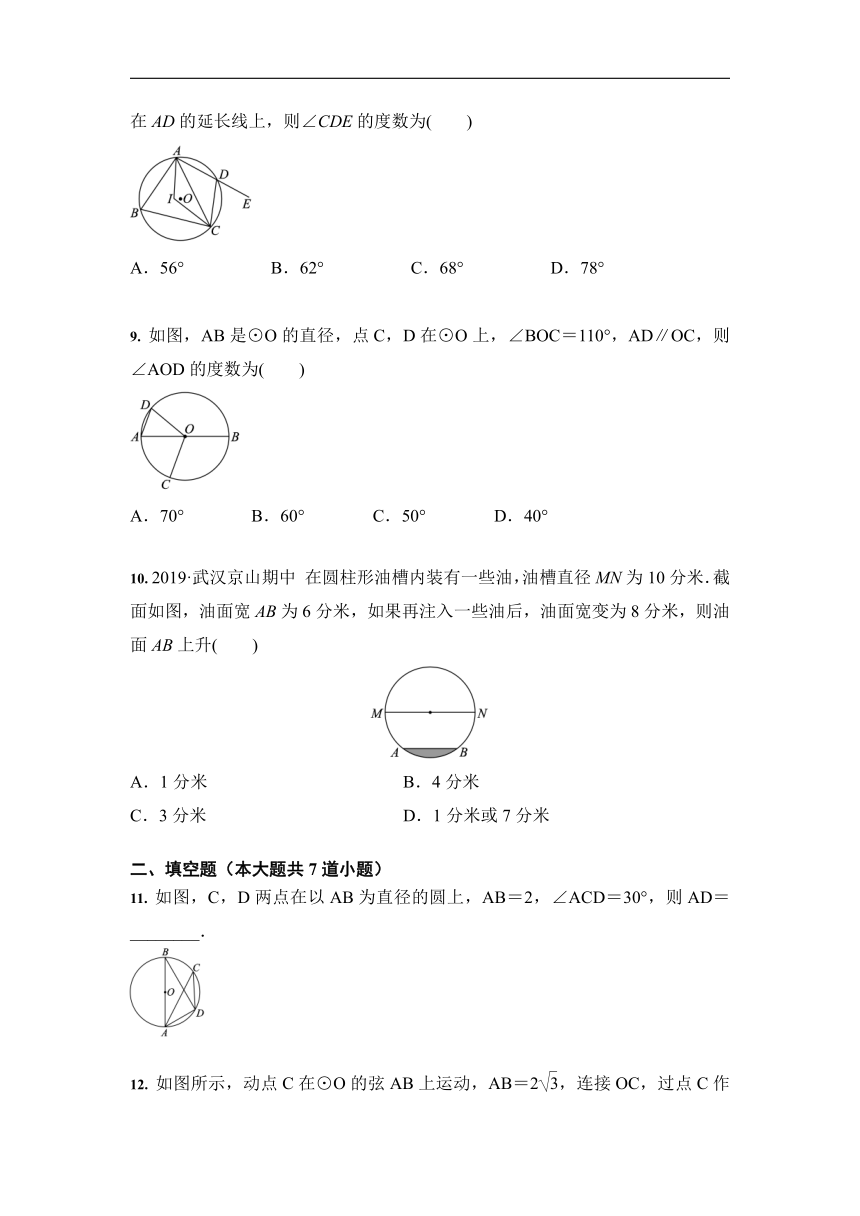
8.
如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
A.56°
B.62°
C.68°
D.78°
9.
如图,AB是⊙O的直径,点C,D在⊙O上,∠BOC=110°,AD∥OC,则∠AOD的度数为( )
A.70°
B.60°
C.50°
D.40°
10.
2019·武汉京山期中
在圆柱形油槽内装有一些油,油槽直径MN为10分米.截面如图,油面宽AB为6分米,如果再注入一些油后,油面宽变为8分米,则油面AB上升( )
A.1分米
B.4分米
C.3分米
D.1分米或7分米
二、填空题(本大题共7道小题)
11.
如图,C,D两点在以AB为直径的圆上,AB=2,∠ACD=30°,则AD=________.
12.
如图所示,动点C在⊙O的弦AB上运动,AB=2,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为________.
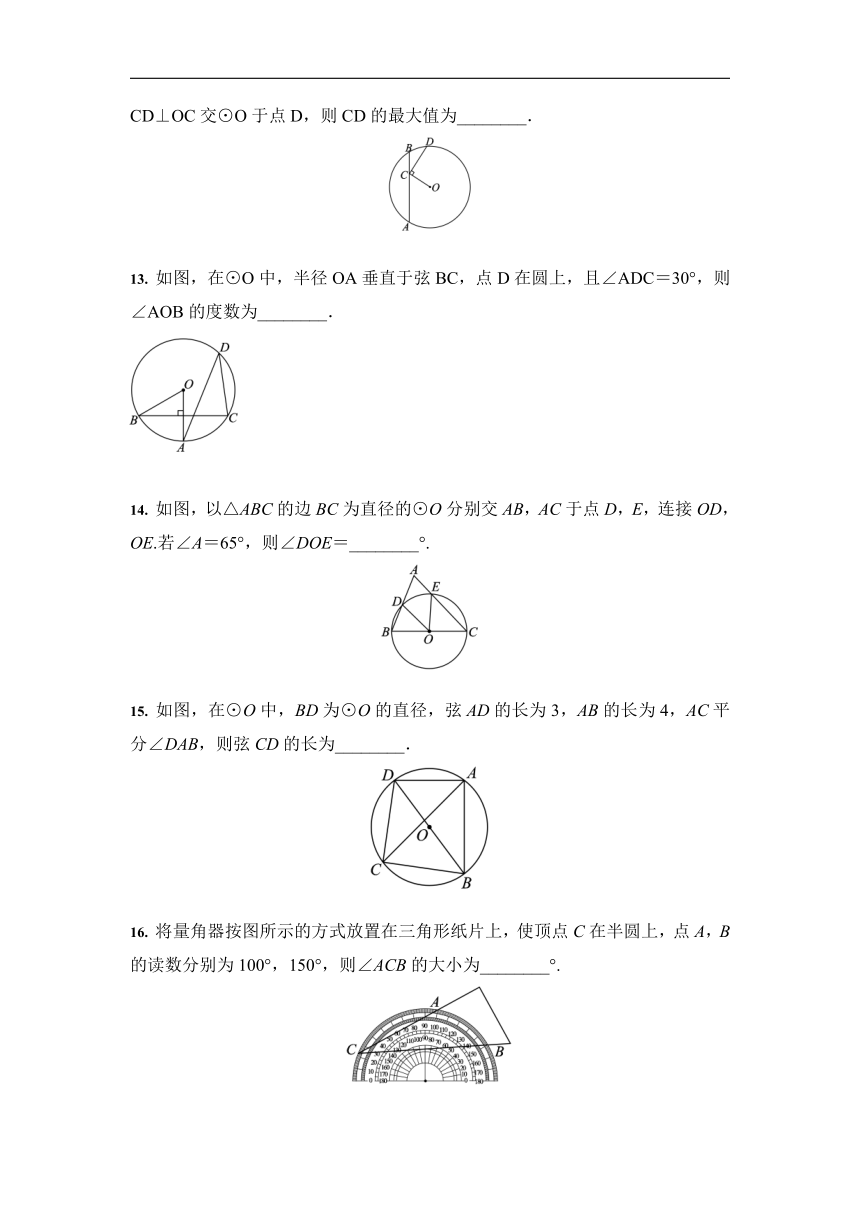
13.
如图,在⊙O中,半径OA垂直于弦BC,点D在圆上,且∠ADC=30°,则∠AOB的度数为________.
14.
如图,以△ABC的边BC为直径的⊙O分别交AB,AC于点D,E,连接OD,OE.若∠A=65°,则∠DOE=________°.
15.
如图,在⊙O中,BD为⊙O的直径,弦AD的长为3,AB的长为4,AC平分∠DAB,则弦CD的长为________.
16.
将量角器按图所示的方式放置在三角形纸片上,使顶点C在半圆上,点A,B的读数分别为100°,150°,则∠ACB的大小为________°.
17.
如图,四边形ABCD内接于⊙O,AB为⊙O的直径,C为弧BD的中点.若∠DAB=40°,则∠ABC=________°.
三、解答题(本大题共4道小题)
18.
如图,在△ABC中,∠C=90°,D是BC边上一点,以BD为直径的⊙O经过AB的中点E,交AD的延长线于点F,连接EF.
(1)求证:∠1=∠F;
(2)若AC=4,EF=2
,求CD的长.
19.
如图,已知⊙O上依次有A,B,C,D四个点,=,连接AB,AD,BD,延长AB到点E,使BE=AB,连接EC,F是EC的中点,连接BF.求证:BF=BD.
20.
如图,在⊙O中,=2,AD⊥OC于点D.求证:AB=2AD.
21.
2018·牡丹江
如图,在⊙O中,=2,AD⊥OC于点D.求证:AB=2AD.
人教版
九年级数学
24.1
圆的有关性质
同步训练-答案
一、选择题(本大题共10道小题)
1.
【答案】B
2.
【答案】B [解析]
AB是⊙O的直径,弦CD⊥AB于点E,由垂径定理可以得到CE=DE,=,=.但并不一定能得到OE=BE,OC=BC,从而A,C,D选项都是错误的.
故选B.
3.
【答案】B
4.
【答案】C
5.
【答案】C
【解析】∵AB为直径,∴,∴,
∵,∴,
在中,.故选C.
6.
【答案】B 【解析】如解图,延长CO交⊙O于点A′,连接A′B.设∠BAC=α,则∠BOC=2∠BAC
=2α,∵∠BAC+∠BOC=180°,∴α+2α=180°,∴α=60°.∴∠BA′C=∠BAC=60°,∵CA′为直径,∴∠A′BC=90°,则在Rt△A′BC中,BC=A′C·sin∠BA′C=2×4×=4.
7.
【答案】A [解析]
连接BI,如图.
∵△ABC的内心为I,
∴∠1=∠2,∠5=∠6.
∵∠3=∠1,
∴∠3=∠2.
∵∠4=∠2+∠6,∠DBI=∠3+∠5,
∴∠4=∠DBI,∴DI=DB.
故选A.
8.
【答案】C [解析]
∵点I是△ABC的内心,
∴∠BAC=2∠IAC,∠ACB=2∠ICA.
∵∠AIC=124°,
∴∠B=180°-(∠BAC+∠ACB)=180°-2(∠IAC+∠ICA)=180°-2(180°-∠AIC)=68°.
又四边形ABCD内接于⊙O,
∴∠CDE=∠B=68°.
9.
【答案】D [解析]
∵∠BOC=110°,∴∠AOC=70°.∵AD∥OC,∴∠A=∠AOC=70°.∵OA=OD,∴∠D=∠A=70°.在△OAD中,∠AOD=180°-(∠A+∠D)=40°.
10.
【答案】D
二、填空题(本大题共7道小题)
11.
【答案】1 [解析]
∵AB为⊙O的直径,
∴∠ADB=90°.
∵∠B=∠ACD=30°,
∴AD=AB=×2=1.
12.
【答案】 [解析]
如图,连接OD,过点O作OH⊥AB于点H,则AH=BH=AB=.∵CD⊥OC,∴CD=.∵OD为⊙O的半径,∴当OC最小时,CD最大.当点C运动到点H时,OC最小,此时CD=BH=,即CD的最大值为.
13.
【答案】60° [解析]
∵OA⊥BC,∴=,∴∠AOB=2∠ADC.∵∠ADC=30°,∴∠AOB=60°.
14.
【答案】50 [解析]
由三角形的内角和定理,得∠B+∠C=180°-∠A.再由OB=OD=OC=OE,得到∠BDO=∠B,∠CEO=∠C.在等腰三角形BOD和等腰三角形COE中,∠DOB+∠EOC=180°-2∠B+180°-2∠C=360°-2(∠B+∠C)=360°-2(180°-∠A)=2∠A,所以∠DOE=180°-2∠A=50°.
15.
【答案】
[解析]
∵BD为⊙O的直径,
∴∠DAB=∠DCB=90°.
∵AD=3,AB=4,∴BD=5.
又∵AC平分∠DAB,∴∠DAC=∠BAC=45°,
∴∠DBC=∠DAC=45°,∠CDB=∠BAC=45°,
从而CD=CB,∴CD= .
16.
【答案】25 [解析]
设量角器的中心为O,由题意可得∠AOB=150°-100°=50°,
所以∠ACB=∠AOB=25°.
17.
【答案】70 [解析]
如图,连接AC.∵AB为⊙O的直径,∴∠ACB=90°.∵C为弧BD的中点,
∴∠CAB=∠DAB=20°,
∴∠ABC=70°.
三、解答题(本大题共4道小题)
18.
【答案】
解:(1)证明:如图,连接DE.
∵BD是⊙O的直径,
∴∠DEB=90°,即DE⊥AB.
又∵E是AB的中点,
∴AD=BD,∴∠1=∠B.
又∵∠B=∠F,∴∠1=∠F.
(2)∵∠1=∠F,∴AE=EF=2
,
∴AB=2AE=4
.
在Rt△ABC中,∵AC=4,∠C=90°,
∴BC==8.
设CD=x,则AD=BD=8-x.
在Rt△ACD中,∵∠C=90°,
∴AC2+CD2=AD2,即42+x2=(8-x)2,
解得x=3,即CD=3.
19.
【答案】
证明:连接AC.
∵AB=BE,F是EC的中点,
∴BF是△EAC的中位线,
∴BF=AC.
∵=,
∴+=+,即=,
∴BD=AC,∴BF=BD.
20.
【答案】
证明:如图,延长AD交⊙O于点E.
∵OC⊥AD,∴=2,AE=2AD.
∵=2,∴=,
∴AB=AE,∴AB=2AD.
21.
【答案】
证明:如图,延长AD交⊙O于点E,
∵OC⊥AD,
∴=2,AE=2AD.
∵=2,∴=,
∴AB=AE,∴AB=2AD.
九年级数学
24.1
圆的有关性质
同步训练
一、选择题(本大题共10道小题)
1.
2018·衢州
如图,点A,B,C在⊙O上,∠ACB=35°,则∠AOB的度数是( )
A.75°
B.70°
C.65°
D.35°
2.
如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论正确的是( )
A.OE=BE
B.=
C.△BOC是等边三角形
D.四边形ODBC是菱形
3.
如图,四边形ABCD是圆内接四边形,E是BC延长线上一点.若∠BAD=105°,则∠DCE的度数为
( )
A.115°
B.105°
C.100°
D.95°
4.
2019·梧州
如图,在半径为的⊙O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是( )
A.2
B.2
C.2
D.4
5.
(2019?广元)如图,AB,AC分别是⊙O的直径和弦,于点D,连接BD,BC,且,,则BD的长为
A.
B.4
C.
D.4.8
6.
如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC,若∠BAC与∠BOC互补,则弦BC的长为( )
A.
3
B.
4
C.
5
D.
6
7.
如图,△ABC的内心为I,连接AI并延长交△ABC的外接圆于点D,则线段DI与DB的关系是( )
A.DI=DB
B.DI>DB
C.DI<DB
D.不确定
8.
如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
A.56°
B.62°
C.68°
D.78°
9.
如图,AB是⊙O的直径,点C,D在⊙O上,∠BOC=110°,AD∥OC,则∠AOD的度数为( )
A.70°
B.60°
C.50°
D.40°
10.
2019·武汉京山期中
在圆柱形油槽内装有一些油,油槽直径MN为10分米.截面如图,油面宽AB为6分米,如果再注入一些油后,油面宽变为8分米,则油面AB上升( )
A.1分米
B.4分米
C.3分米
D.1分米或7分米
二、填空题(本大题共7道小题)
11.
如图,C,D两点在以AB为直径的圆上,AB=2,∠ACD=30°,则AD=________.
12.
如图所示,动点C在⊙O的弦AB上运动,AB=2,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为________.
13.
如图,在⊙O中,半径OA垂直于弦BC,点D在圆上,且∠ADC=30°,则∠AOB的度数为________.
14.
如图,以△ABC的边BC为直径的⊙O分别交AB,AC于点D,E,连接OD,OE.若∠A=65°,则∠DOE=________°.
15.
如图,在⊙O中,BD为⊙O的直径,弦AD的长为3,AB的长为4,AC平分∠DAB,则弦CD的长为________.
16.
将量角器按图所示的方式放置在三角形纸片上,使顶点C在半圆上,点A,B的读数分别为100°,150°,则∠ACB的大小为________°.
17.
如图,四边形ABCD内接于⊙O,AB为⊙O的直径,C为弧BD的中点.若∠DAB=40°,则∠ABC=________°.
三、解答题(本大题共4道小题)
18.
如图,在△ABC中,∠C=90°,D是BC边上一点,以BD为直径的⊙O经过AB的中点E,交AD的延长线于点F,连接EF.
(1)求证:∠1=∠F;
(2)若AC=4,EF=2
,求CD的长.
19.
如图,已知⊙O上依次有A,B,C,D四个点,=,连接AB,AD,BD,延长AB到点E,使BE=AB,连接EC,F是EC的中点,连接BF.求证:BF=BD.
20.
如图,在⊙O中,=2,AD⊥OC于点D.求证:AB=2AD.
21.
2018·牡丹江
如图,在⊙O中,=2,AD⊥OC于点D.求证:AB=2AD.
人教版
九年级数学
24.1
圆的有关性质
同步训练-答案
一、选择题(本大题共10道小题)
1.
【答案】B
2.
【答案】B [解析]
AB是⊙O的直径,弦CD⊥AB于点E,由垂径定理可以得到CE=DE,=,=.但并不一定能得到OE=BE,OC=BC,从而A,C,D选项都是错误的.
故选B.
3.
【答案】B
4.
【答案】C
5.
【答案】C
【解析】∵AB为直径,∴,∴,
∵,∴,
在中,.故选C.
6.
【答案】B 【解析】如解图,延长CO交⊙O于点A′,连接A′B.设∠BAC=α,则∠BOC=2∠BAC
=2α,∵∠BAC+∠BOC=180°,∴α+2α=180°,∴α=60°.∴∠BA′C=∠BAC=60°,∵CA′为直径,∴∠A′BC=90°,则在Rt△A′BC中,BC=A′C·sin∠BA′C=2×4×=4.
7.
【答案】A [解析]
连接BI,如图.
∵△ABC的内心为I,
∴∠1=∠2,∠5=∠6.
∵∠3=∠1,
∴∠3=∠2.
∵∠4=∠2+∠6,∠DBI=∠3+∠5,
∴∠4=∠DBI,∴DI=DB.
故选A.
8.
【答案】C [解析]
∵点I是△ABC的内心,
∴∠BAC=2∠IAC,∠ACB=2∠ICA.
∵∠AIC=124°,
∴∠B=180°-(∠BAC+∠ACB)=180°-2(∠IAC+∠ICA)=180°-2(180°-∠AIC)=68°.
又四边形ABCD内接于⊙O,
∴∠CDE=∠B=68°.
9.
【答案】D [解析]
∵∠BOC=110°,∴∠AOC=70°.∵AD∥OC,∴∠A=∠AOC=70°.∵OA=OD,∴∠D=∠A=70°.在△OAD中,∠AOD=180°-(∠A+∠D)=40°.
10.
【答案】D
二、填空题(本大题共7道小题)
11.
【答案】1 [解析]
∵AB为⊙O的直径,
∴∠ADB=90°.
∵∠B=∠ACD=30°,
∴AD=AB=×2=1.
12.
【答案】 [解析]
如图,连接OD,过点O作OH⊥AB于点H,则AH=BH=AB=.∵CD⊥OC,∴CD=.∵OD为⊙O的半径,∴当OC最小时,CD最大.当点C运动到点H时,OC最小,此时CD=BH=,即CD的最大值为.
13.
【答案】60° [解析]
∵OA⊥BC,∴=,∴∠AOB=2∠ADC.∵∠ADC=30°,∴∠AOB=60°.
14.
【答案】50 [解析]
由三角形的内角和定理,得∠B+∠C=180°-∠A.再由OB=OD=OC=OE,得到∠BDO=∠B,∠CEO=∠C.在等腰三角形BOD和等腰三角形COE中,∠DOB+∠EOC=180°-2∠B+180°-2∠C=360°-2(∠B+∠C)=360°-2(180°-∠A)=2∠A,所以∠DOE=180°-2∠A=50°.
15.
【答案】
[解析]
∵BD为⊙O的直径,
∴∠DAB=∠DCB=90°.
∵AD=3,AB=4,∴BD=5.
又∵AC平分∠DAB,∴∠DAC=∠BAC=45°,
∴∠DBC=∠DAC=45°,∠CDB=∠BAC=45°,
从而CD=CB,∴CD= .
16.
【答案】25 [解析]
设量角器的中心为O,由题意可得∠AOB=150°-100°=50°,
所以∠ACB=∠AOB=25°.
17.
【答案】70 [解析]
如图,连接AC.∵AB为⊙O的直径,∴∠ACB=90°.∵C为弧BD的中点,
∴∠CAB=∠DAB=20°,
∴∠ABC=70°.
三、解答题(本大题共4道小题)
18.
【答案】
解:(1)证明:如图,连接DE.
∵BD是⊙O的直径,
∴∠DEB=90°,即DE⊥AB.
又∵E是AB的中点,
∴AD=BD,∴∠1=∠B.
又∵∠B=∠F,∴∠1=∠F.
(2)∵∠1=∠F,∴AE=EF=2
,
∴AB=2AE=4
.
在Rt△ABC中,∵AC=4,∠C=90°,
∴BC==8.
设CD=x,则AD=BD=8-x.
在Rt△ACD中,∵∠C=90°,
∴AC2+CD2=AD2,即42+x2=(8-x)2,
解得x=3,即CD=3.
19.
【答案】
证明:连接AC.
∵AB=BE,F是EC的中点,
∴BF是△EAC的中位线,
∴BF=AC.
∵=,
∴+=+,即=,
∴BD=AC,∴BF=BD.
20.
【答案】
证明:如图,延长AD交⊙O于点E.
∵OC⊥AD,∴=2,AE=2AD.
∵=2,∴=,
∴AB=AE,∴AB=2AD.
21.
【答案】
证明:如图,延长AD交⊙O于点E,
∵OC⊥AD,
∴=2,AE=2AD.
∵=2,∴=,
∴AB=AE,∴AB=2AD.
同课章节目录
