人教版 九年级下册数学 26.1 反比例函数 同步训练(word版含解析)
文档属性
| 名称 | 人教版 九年级下册数学 26.1 反比例函数 同步训练(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 319.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 10:42:58 | ||
图片预览

文档简介
人教版
九年级数学
26.1
反比例函数
同步训练
一、选择题(本大题共10道小题)
1.
函数y=的图象经过点A(1,-2),则k的值为( )
A.
B.
-
C.
2
D.
-2
2.
如图,在平面直角坐标系中,Rt△ABC的顶点A,C的坐标分别是(0,3),(3,0),∠ACB=90°,AC=2BC,函数y=(k>0,x>0)的图象经过点B,则k的值为
( )
A.
B.9
C.
D.
3.
(2019·广东广州)若点A(﹣1,y1),B(2,y2),C(3,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是
A.y3B.y2C.y1D.y14.
(2019·江苏扬州)若反比例函数的图象上有两个不同的点关于y轴对称点都在一次函数y=–x+m的图象上,则m的取值范围是
A.
B.
C.
D.
5.
反比例函数y=-的图象上有两点P1(x1,y1),P2(x2,y2),若x1<0A.
y1 B.
y1<0 C.
y1>y2>0
D.
y1>0>y2
6.
(2019·江西)已知正比例函数y1的图象与反比例函数y2的图象相交于点A(2,4),下列说法正确的是
A.反比例函数y2的解析式是y2=–
B.两个函数图象的另一交点坐标为(2,–4)
C.当x<–2或0D.正比例函数y1与反比例函数y2都随x的增大而增大
7.
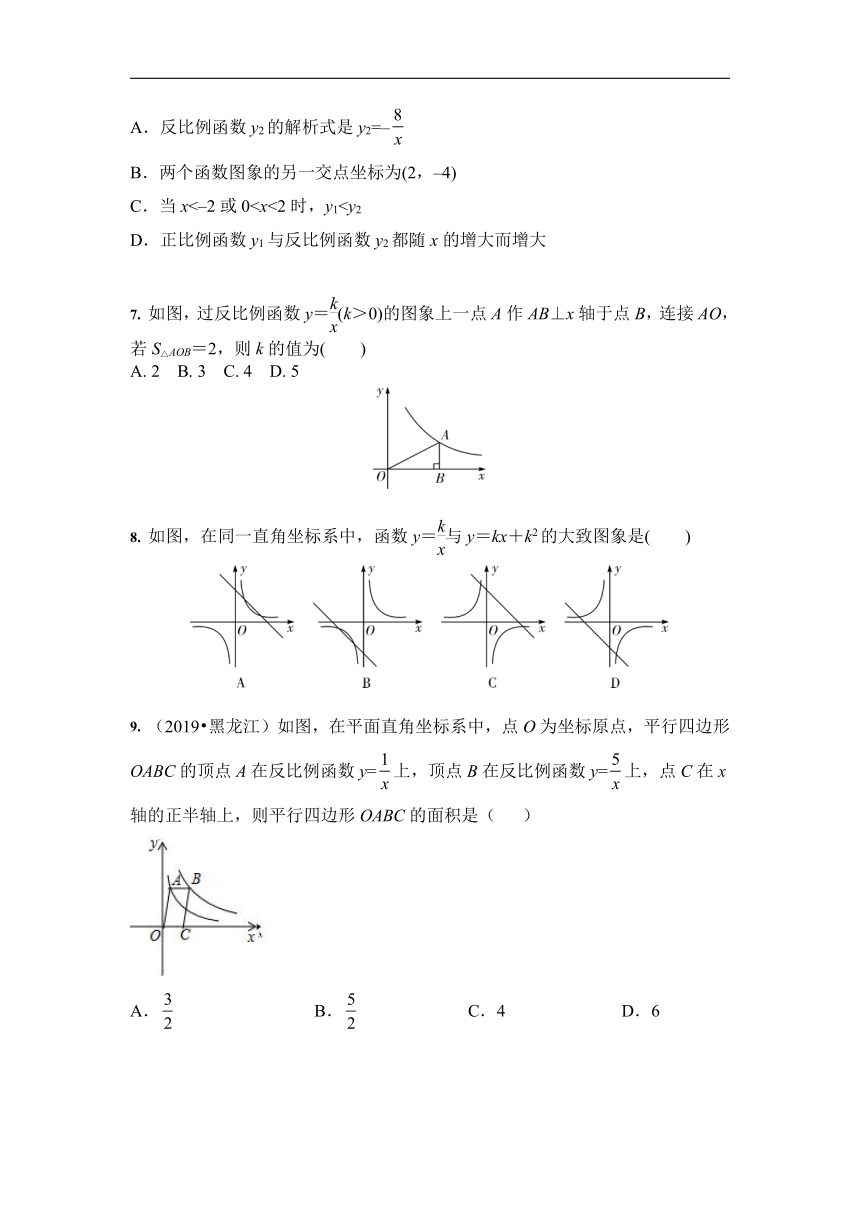
如图,过反比例函数y=(k>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=2,则k的值为( )
A.
2
B.
3
C.
4
D.
5
8.
如图,在同一直角坐标系中,函数y=与y=kx+k2的大致图象是( )
9.
(2019?黑龙江)如图,在平面直角坐标系中,点O为坐标原点,平行四边形OABC的顶点A在反比例函数y=上,顶点B在反比例函数y=上,点C在x轴的正半轴上,则平行四边形OABC的面积是(
)
A.
B.
C.4
D.6
10.
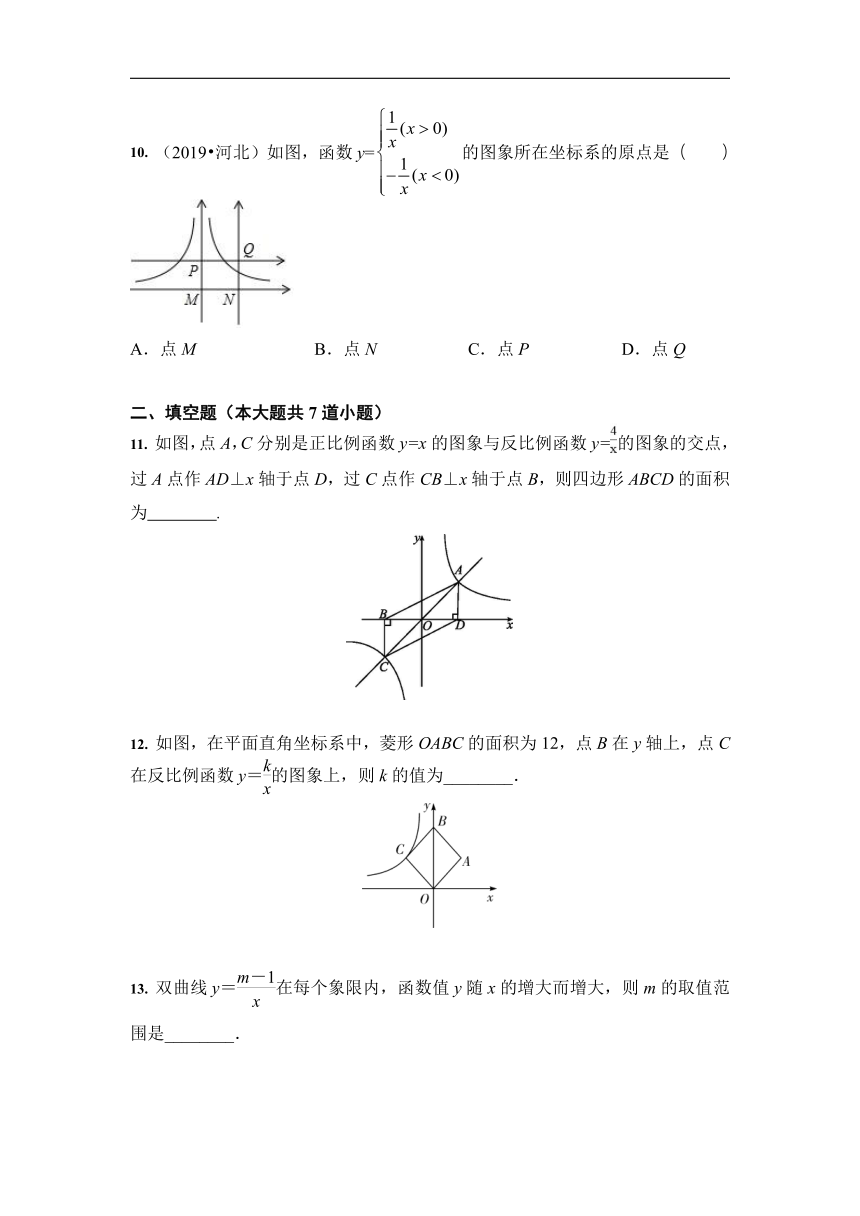
(2019?河北)如图,函数y=的图象所在坐标系的原点是(
)
A.点M
B.点N
C.点P
D.点Q
二、填空题(本大题共7道小题)
11.
如图,点A,C分别是正比例函数y=x的图象与反比例函数y=的图象的交点,过A点作AD⊥x轴于点D,过C点作CB⊥x轴于点B,则四边形ABCD的面积为 .?
12.
如图,在平面直角坐标系中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=的图象上,则k的值为________.
13.
双曲线y=在每个象限内,函数值y随x的增大而增大,则m的取值范围是________.
14.
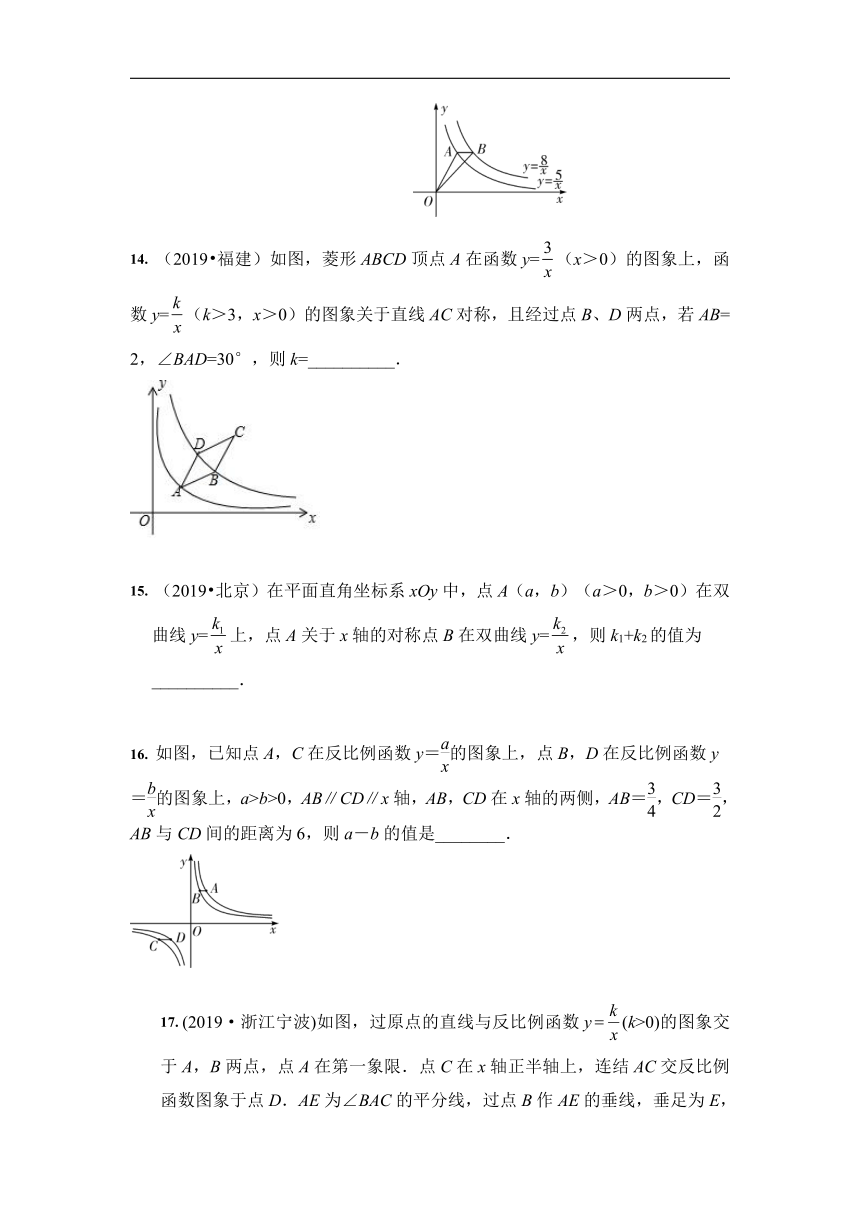
(2019?福建)如图,菱形ABCD顶点A在函数y=(x>0)的图象上,函数y=(k>3,x>0)的图象关于直线AC对称,且经过点B、D两点,若AB=2,∠BAD=30°,则k=__________.
15.
(2019?北京)在平面直角坐标系xOy中,点A(a,b)(a>0,b>0)在双曲线y=上,点A关于x轴的对称点B在双曲线y=,则k1+k2的值为__________.
16.
如图,已知点A,C在反比例函数y=的图象上,点B,D在反比例函数y=的图象上,a>b>0,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=,CD=,AB与CD间的距离为6,则a-b的值是________.
17.
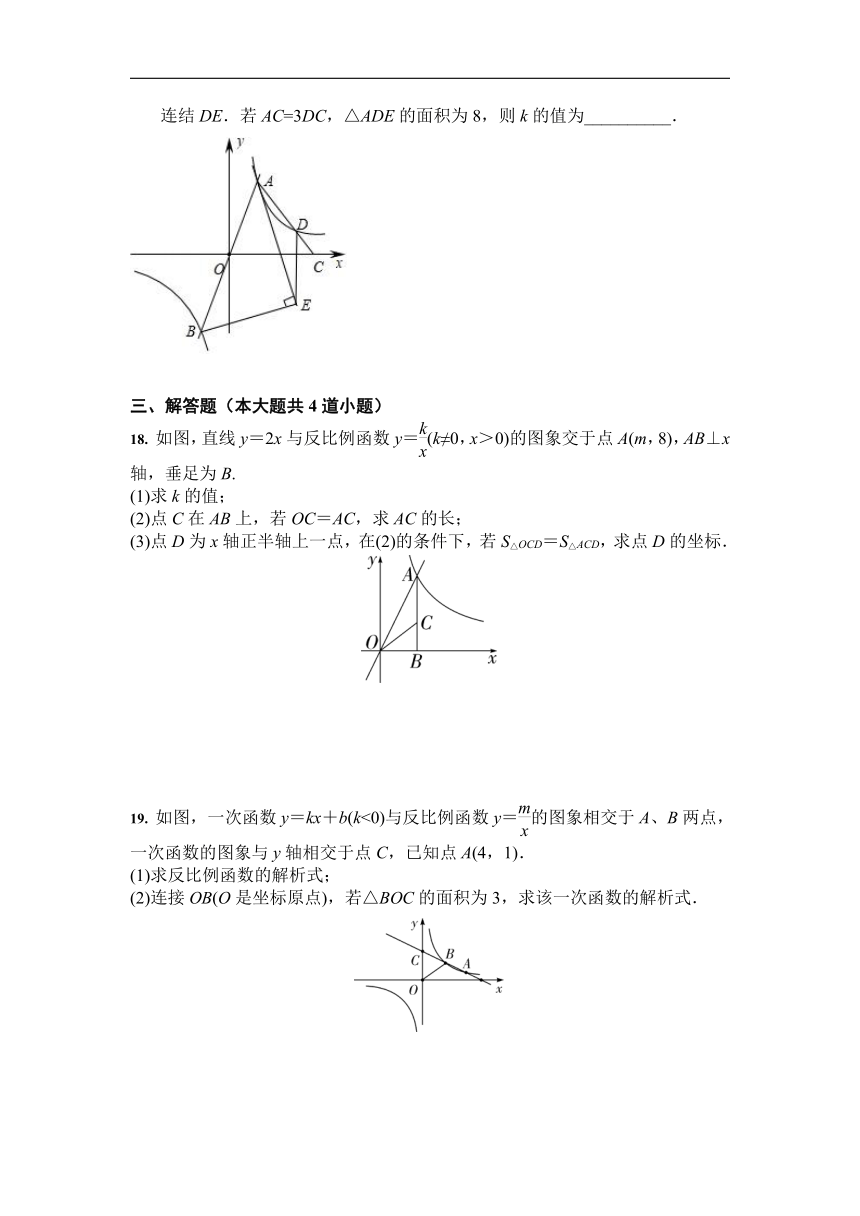
(2019·浙江宁波)如图,过原点的直线与反比例函数y(k>0)的图象交于A,B两点,点A在第一象限.点C在x轴正半轴上,连结AC交反比例函数图象于点D.AE为∠BAC的平分线,过点B作AE的垂线,垂足为E,连结DE.若AC=3DC,△ADE的面积为8,则k的值为__________.
三、解答题(本大题共4道小题)
18.
如图,直线y=2x与反比例函数y=(k≠0,x>0)的图象交于点A(m,8),AB⊥x轴,垂足为B.
(1)求k的值;
(2)点C在AB上,若OC=AC,求AC的长;
(3)点D为x轴正半轴上一点,在(2)的条件下,若S△OCD=S△ACD,求点D的坐标.
19.
如图,一次函数y=kx+b(k<0)与反比例函数y=的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1).
(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
20.
如图,一次函数y=kx+b的图象与反比例函数y=(x>0)的图象交于A(2,-1),B(,n)两点,直线y=2与y轴交于点C.
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
21.
(2019·浙江舟山)如图,在直角坐标系中,已知点B(4,0),等边三角形OAB的顶点A在反比例函数y的图象上.
(1)求反比例函数的表达式.
(2)把△OAB向右平移a个单位长度,对应得到△O'A'B',当这个函数图象经过△O'A'B'一边的中点时,求a的值.
人教版
九年级数学
26.1
反比例函数
同步训练-答案
一、选择题(本大题共10道小题)
1.
【答案】D 【解析】本题考查学生求反比例函数解析式的方法.解题思路:利用图象上的点满足函数解析式,将A(1,-2)代入y=可求得:k=-2.
2.
【答案】D [解析]过B作BD⊥x轴,垂足为D.
∵A,C的坐标分别为(0,3),(3,0),
∴OA=OC=3,∠ACO=45°,∴AC=3.
∵AC=2BC,∴BC=.
∵∠ACB=90°,
∴∠BCD=45°,∴BD=CD=,∴点B的坐标为.
∵函数y=(k>0,x>0)的图象经过点B,
∴k==,故选D.
3.
【答案】C
【解析】∵点A(﹣1,y1),B(2,y2),C(3,y3)在反比例函数y=的图象上,∴y1==﹣6,y2==3,y3==2,又∵﹣6<2<3,∴y14.
【答案】C
【解析】∵反比例函数上两个不同的点关于y轴对称的点,在一次函数y=–x+m图象上,∴反比例函数与一次函数y=–x+m有两个不同的交点,联立两个函数解方程,∵有两个不同的交点,∴有两个不等的根,∴Δ=m2–8>0,∴m>2或m<–2,故选C.
5.
【答案】D 【解析】根据反比例函数的性质或者利用特殊值法即可作出选择.方法一:∵反比例函数y=-中k=-1<0,∴当x<0时,y>0;当x>0时,y<0.又∵x1<0<x2,∴y1>0>y2.故选D.方法二:令x1=-1,则y1=1,令x2=1,则y2=-1,∴y1>0>y2.
6.
【答案】C
【解析】∵正比例函数y1的图象与反比例函数y2的图象相交于点A(2,4),
∴正比例函数y1=2x,反比例函数y2=,
∴两个函数图象的另一个交点为(–2,–4),
∴A,B选项错误;
∵正比例函数y1=2x中,y随x的增大而增大,反比例函数y2=中,在每个象限内y随x的增大而减小,∴D选项错误,
∵当x<–2或0故选C.
7.
【答案】C 【解析】
∵点A在反比例函数y=的图象上,且AB⊥x轴于点B,设点A坐标为(x,y),∴k=xy,∵点A在第一象限,∴x、y都是正数,∴S△AOB=OB·AB=xy,∵S△AOB=2,∴k=xy=4.
8.
【答案】C 【解析】当k>0时,反比例函数y=图象的两个分支分别位于第一、三象限,直线y=kx+k2经过第一、二、三象限,没有符合题意的选项;当k<0时,反比例函数y=图象的两个分支分别位于第二、四象限,直线y=kx+k2经过第一、二、四象限,只有C符合题意.
9.
【答案】C
【解析】如图,过点B作BD⊥x轴于D,延长BA交y轴于E,
∵四边形OABC是平行四边形,∴AB∥OC,OA=BC,
∴BE⊥y轴,∴OE=BD,∴Rt△AOE≌Rt△CBD(HL),
根据系数k的几何意义,S矩形BDOE=5,S△AOE=,
∴四边形OABC的面积=5––=4,
故选C.
10.
【答案】A
【解析】由已知可知函数y=关于y轴对称,所以点M是原点;故选A.
二、填空题(本大题共7道小题)
11.
【答案】8 [解析]由得或,
∴A的坐标为(2,2),C的坐标为(-2,-2).
∵AD⊥x轴于点D,CB⊥x轴于点B,∴B(-2,0),D(2,0),∴BD=4,AD=2,
∴四边形ABCD的面积=AD·BD×2=8.
12.
【答案】-6 【解析】如解图,连接AC交y轴于点D,因为四边形ABCO是菱形,且面积为12,则△OCD的面积为3,利用反比例函数k的几何意义可得k=-6.
13.
【答案】m<1 【解析】∵在每个象限内,函数值y随x的增大而增大,∴双曲线在二、四象限内,∴在函数y=中,m-1<0,即m<1.
14.
【答案】6+2
【解析】连接OC,AC,过A作AE⊥x轴于点E,延长DA与x轴交于点F,过点D作DG⊥x轴于点G,
∵函数y=(k>3,x>0)的图象关于直线AC对称,
∴O、A、C三点在同直线上,且∠COE=45°,∴OE=AE,
不妨设OE=AE=a,则A(a,a),
∵点A在反比例函数y=(x>0)的图象上,
∴a2=3,∴a=,∴AE=OE=,
∵∠BAD=30°,∴∠OAF=∠CAD=∠BAD=15°,
∵∠OAE=∠AOE=45°,∴∠EAF=30°,∴AF==2,EF=AEtan30°=1,
∵AB=AD=2,∴AF=AD=2,又∵AE∥DG,∴EF=EG=1,DG=2AE=2,
∴OG=OE+EG=+1,∴D(+1,2),∴k=2×(+1)=6+2.
故答案为:6+2.
15.
【答案】0
【解析】∵点A(a,b)(a>0,b>0)在双曲线y=上,∴k1=ab;
又∵点A与点B关于x轴对称,∴B(a,–b),
∵点B在双曲线y=上,∴k2=–ab;∴k1+k2=ab+(–ab)=0;
故答案为:0.
16.
【答案】3 【解析】设点A的纵坐标为y1,点C的纵坐标为y2,∵AB∥CD∥x轴,∴点B的纵坐标为y1,点D的纵坐标为y2,∵点A在函数y=的图象上,点B在函数y=的图象上,且AB=,∴-=,∴y1=,同理y2=,又∵AB与CD间的距离为6,∴y1-
y2=-=6,解得a-b=3.
17.
【答案】6
【解析】如图,连接OE,CE,过点A作AF⊥x轴,过点D作DH⊥x轴,过点D作DG⊥AF,
∵过原点的直线与反比例函数y(k>0)的图象交于A,B两点,
∴A与B关于原点对称,
∴O是AB的中点,
∵BE⊥AE,
∴OE=OA,
∴∠OAE=∠AEO,
∵AE为∠BAC的平分线,
∴∠BAE=∠DAE,
∴∠DAE=∠AEO,
∴AD∥OE,
∴S△ACE=S△AOC,
∵AC=3DC,△ADE的面积为8,
∴S△ACE=S△AOC=12,
设点A(m,),
∵AC=3DC,DH∥AF,
∴3DH=AF,
∴D(3m,),
∵CH∥GD,AG∥DH,
∴△DHC∽△AGD,
∴S△HDCS△ADG,
∵S△AOC=S△AOF+S梯形AFHD+S△HDC(DH+AF)×FH+S△HDC2m12,
∴2k=12,∴k=6;
故答案为6.
三、解答题(本大题共4道小题)
18.
【答案】
(1)∵直线y=2x与反比例函数y=(k≠0,x>0)的图象交于点A(m,8),则2m=8,
解得m=4,
∴A(4,8),
∴k=4×8=32;
(2)设AC=x,则OC=x,BC=8-x,
在Rt△OBC中,由勾股定理得:OC2=OB2+BC2,
即x2=42+(8-x)2,解得x=5,∴AC=5;
(3)设点D的坐标为(x,0).分两种情况:
①当x>4时,如解图①,∵S△OCD=S△ACD,
∴OD·BC=AC·BD,
∴3x=5(x-4),解得x=10;
②当0<x<4时,如解图②,同理得:3x=5(4-x),解得x=.
∴点D的坐标为(10,0)或(,0).
19.
【答案】
解:(1)把A(4,1)代入y=得1=.
∴m=4,(2分)
∴反比例函数的解析式为y=.(3分)
(2)过点B作BE⊥y轴于点E,如解图,设点B坐标为(n,),则OE=,BE=n.
∴S△BEO=OE·BE=2,(4分)
∵S△BOC=3,
∴S△BCE=1,
∴OE∶EC=2∶1,
∴CE=,OC=.(6分)
设直线AB的解析式为y=kx+,把(n,)和(4,1)分别代入得:,
解得 ,(7分)
∴=3,
∴一次函数的解析式为y=-x+3.(8分)
20.
【答案】
解:(1)∵点A(2,-1)在反比例函数y=的图象上,
∴-1=,即m=-2.(1分)
∴反比例函数的解析式为y=-.(2分)
∵点B(,n)在反比例函数y=-的图象上,
∴n=-=-4,即点B的坐标为(,-4).
将点A(2,-1)和点B(,-4)分别代入y=kx+b,得
,解得,
∴一次函数的解析式为y=2x-5.(5分)
(2)如解图,设直线AB交y轴于点D.
令y=2x-5中x=0,得y=-5,即点D的坐标是(0,-5),
∴OD=5.(7分)
∵直线y=2与y轴交于点C,
∴C点的坐标是(0,2),(8分)
∴CD=OC+OD=7.
∴S△ABC=S△ACD-S△BCD=×7×2-×7×=7-=.(10分)
21.
【答案】
(1)反比例函数的解析式为y;(2)a的值为1或3.
【解析】(1)如图1,过点A作AC⊥OB于点C,
∵△OAB是等边三角形,
∴∠AOB=60°,OCOB,
∵B(4,0),
∴OB=OA=4,
∴OC=2,AC=2.
把点A(2,2)代入y,解得k=4.
∴反比例函数的解析式为y;
(2)分两种情况讨论:
①当点D是A′B′的中点,如图2,过点D作DE⊥x轴于点E.
由题意得A′B′=4,∠A′B′E=60°,
在Rt△DEB′中,B′D=2,DE=,B′E=1.
∴O′E=3,
把y代入y,得x=4,
∴OE=4,∴a=OO′=1;
②如图3,点F是A′O′的中点,过点F作FH⊥x轴于点H.
由题意得A′O′=4,∠A′O′B′=60°,
在Rt△FO′H中,FH,O′H=1.
把y代入y,得x=4,
∴OH=4,∴a=OO′=3,
综上所述,a的值为1或3.
九年级数学
26.1
反比例函数
同步训练
一、选择题(本大题共10道小题)
1.
函数y=的图象经过点A(1,-2),则k的值为( )
A.
B.
-
C.
2
D.
-2
2.
如图,在平面直角坐标系中,Rt△ABC的顶点A,C的坐标分别是(0,3),(3,0),∠ACB=90°,AC=2BC,函数y=(k>0,x>0)的图象经过点B,则k的值为
( )
A.
B.9
C.
D.
3.
(2019·广东广州)若点A(﹣1,y1),B(2,y2),C(3,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是
A.y3
(2019·江苏扬州)若反比例函数的图象上有两个不同的点关于y轴对称点都在一次函数y=–x+m的图象上,则m的取值范围是
A.
B.
C.
D.
5.
反比例函数y=-的图象上有两点P1(x1,y1),P2(x2,y2),若x1<0
y1
y1<0
y1>y2>0
D.
y1>0>y2
6.
(2019·江西)已知正比例函数y1的图象与反比例函数y2的图象相交于点A(2,4),下列说法正确的是
A.反比例函数y2的解析式是y2=–
B.两个函数图象的另一交点坐标为(2,–4)
C.当x<–2或0
7.
如图,过反比例函数y=(k>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=2,则k的值为( )
A.
2
B.
3
C.
4
D.
5
8.
如图,在同一直角坐标系中,函数y=与y=kx+k2的大致图象是( )
9.
(2019?黑龙江)如图,在平面直角坐标系中,点O为坐标原点,平行四边形OABC的顶点A在反比例函数y=上,顶点B在反比例函数y=上,点C在x轴的正半轴上,则平行四边形OABC的面积是(
)
A.
B.
C.4
D.6
10.
(2019?河北)如图,函数y=的图象所在坐标系的原点是(
)
A.点M
B.点N
C.点P
D.点Q
二、填空题(本大题共7道小题)
11.
如图,点A,C分别是正比例函数y=x的图象与反比例函数y=的图象的交点,过A点作AD⊥x轴于点D,过C点作CB⊥x轴于点B,则四边形ABCD的面积为 .?
12.
如图,在平面直角坐标系中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=的图象上,则k的值为________.
13.
双曲线y=在每个象限内,函数值y随x的增大而增大,则m的取值范围是________.
14.
(2019?福建)如图,菱形ABCD顶点A在函数y=(x>0)的图象上,函数y=(k>3,x>0)的图象关于直线AC对称,且经过点B、D两点,若AB=2,∠BAD=30°,则k=__________.
15.
(2019?北京)在平面直角坐标系xOy中,点A(a,b)(a>0,b>0)在双曲线y=上,点A关于x轴的对称点B在双曲线y=,则k1+k2的值为__________.
16.
如图,已知点A,C在反比例函数y=的图象上,点B,D在反比例函数y=的图象上,a>b>0,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=,CD=,AB与CD间的距离为6,则a-b的值是________.
17.
(2019·浙江宁波)如图,过原点的直线与反比例函数y(k>0)的图象交于A,B两点,点A在第一象限.点C在x轴正半轴上,连结AC交反比例函数图象于点D.AE为∠BAC的平分线,过点B作AE的垂线,垂足为E,连结DE.若AC=3DC,△ADE的面积为8,则k的值为__________.
三、解答题(本大题共4道小题)
18.
如图,直线y=2x与反比例函数y=(k≠0,x>0)的图象交于点A(m,8),AB⊥x轴,垂足为B.
(1)求k的值;
(2)点C在AB上,若OC=AC,求AC的长;
(3)点D为x轴正半轴上一点,在(2)的条件下,若S△OCD=S△ACD,求点D的坐标.
19.
如图,一次函数y=kx+b(k<0)与反比例函数y=的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1).
(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
20.
如图,一次函数y=kx+b的图象与反比例函数y=(x>0)的图象交于A(2,-1),B(,n)两点,直线y=2与y轴交于点C.
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
21.
(2019·浙江舟山)如图,在直角坐标系中,已知点B(4,0),等边三角形OAB的顶点A在反比例函数y的图象上.
(1)求反比例函数的表达式.
(2)把△OAB向右平移a个单位长度,对应得到△O'A'B',当这个函数图象经过△O'A'B'一边的中点时,求a的值.
人教版
九年级数学
26.1
反比例函数
同步训练-答案
一、选择题(本大题共10道小题)
1.
【答案】D 【解析】本题考查学生求反比例函数解析式的方法.解题思路:利用图象上的点满足函数解析式,将A(1,-2)代入y=可求得:k=-2.
2.
【答案】D [解析]过B作BD⊥x轴,垂足为D.
∵A,C的坐标分别为(0,3),(3,0),
∴OA=OC=3,∠ACO=45°,∴AC=3.
∵AC=2BC,∴BC=.
∵∠ACB=90°,
∴∠BCD=45°,∴BD=CD=,∴点B的坐标为.
∵函数y=(k>0,x>0)的图象经过点B,
∴k==,故选D.
3.
【答案】C
【解析】∵点A(﹣1,y1),B(2,y2),C(3,y3)在反比例函数y=的图象上,∴y1==﹣6,y2==3,y3==2,又∵﹣6<2<3,∴y1
【答案】C
【解析】∵反比例函数上两个不同的点关于y轴对称的点,在一次函数y=–x+m图象上,∴反比例函数与一次函数y=–x+m有两个不同的交点,联立两个函数解方程,∵有两个不同的交点,∴有两个不等的根,∴Δ=m2–8>0,∴m>2或m<–2,故选C.
5.
【答案】D 【解析】根据反比例函数的性质或者利用特殊值法即可作出选择.方法一:∵反比例函数y=-中k=-1<0,∴当x<0时,y>0;当x>0时,y<0.又∵x1<0<x2,∴y1>0>y2.故选D.方法二:令x1=-1,则y1=1,令x2=1,则y2=-1,∴y1>0>y2.
6.
【答案】C
【解析】∵正比例函数y1的图象与反比例函数y2的图象相交于点A(2,4),
∴正比例函数y1=2x,反比例函数y2=,
∴两个函数图象的另一个交点为(–2,–4),
∴A,B选项错误;
∵正比例函数y1=2x中,y随x的增大而增大,反比例函数y2=中,在每个象限内y随x的增大而减小,∴D选项错误,
∵当x<–2或0
7.
【答案】C 【解析】
∵点A在反比例函数y=的图象上,且AB⊥x轴于点B,设点A坐标为(x,y),∴k=xy,∵点A在第一象限,∴x、y都是正数,∴S△AOB=OB·AB=xy,∵S△AOB=2,∴k=xy=4.
8.
【答案】C 【解析】当k>0时,反比例函数y=图象的两个分支分别位于第一、三象限,直线y=kx+k2经过第一、二、三象限,没有符合题意的选项;当k<0时,反比例函数y=图象的两个分支分别位于第二、四象限,直线y=kx+k2经过第一、二、四象限,只有C符合题意.
9.
【答案】C
【解析】如图,过点B作BD⊥x轴于D,延长BA交y轴于E,
∵四边形OABC是平行四边形,∴AB∥OC,OA=BC,
∴BE⊥y轴,∴OE=BD,∴Rt△AOE≌Rt△CBD(HL),
根据系数k的几何意义,S矩形BDOE=5,S△AOE=,
∴四边形OABC的面积=5––=4,
故选C.
10.
【答案】A
【解析】由已知可知函数y=关于y轴对称,所以点M是原点;故选A.
二、填空题(本大题共7道小题)
11.
【答案】8 [解析]由得或,
∴A的坐标为(2,2),C的坐标为(-2,-2).
∵AD⊥x轴于点D,CB⊥x轴于点B,∴B(-2,0),D(2,0),∴BD=4,AD=2,
∴四边形ABCD的面积=AD·BD×2=8.
12.
【答案】-6 【解析】如解图,连接AC交y轴于点D,因为四边形ABCO是菱形,且面积为12,则△OCD的面积为3,利用反比例函数k的几何意义可得k=-6.
13.
【答案】m<1 【解析】∵在每个象限内,函数值y随x的增大而增大,∴双曲线在二、四象限内,∴在函数y=中,m-1<0,即m<1.
14.
【答案】6+2
【解析】连接OC,AC,过A作AE⊥x轴于点E,延长DA与x轴交于点F,过点D作DG⊥x轴于点G,
∵函数y=(k>3,x>0)的图象关于直线AC对称,
∴O、A、C三点在同直线上,且∠COE=45°,∴OE=AE,
不妨设OE=AE=a,则A(a,a),
∵点A在反比例函数y=(x>0)的图象上,
∴a2=3,∴a=,∴AE=OE=,
∵∠BAD=30°,∴∠OAF=∠CAD=∠BAD=15°,
∵∠OAE=∠AOE=45°,∴∠EAF=30°,∴AF==2,EF=AEtan30°=1,
∵AB=AD=2,∴AF=AD=2,又∵AE∥DG,∴EF=EG=1,DG=2AE=2,
∴OG=OE+EG=+1,∴D(+1,2),∴k=2×(+1)=6+2.
故答案为:6+2.
15.
【答案】0
【解析】∵点A(a,b)(a>0,b>0)在双曲线y=上,∴k1=ab;
又∵点A与点B关于x轴对称,∴B(a,–b),
∵点B在双曲线y=上,∴k2=–ab;∴k1+k2=ab+(–ab)=0;
故答案为:0.
16.
【答案】3 【解析】设点A的纵坐标为y1,点C的纵坐标为y2,∵AB∥CD∥x轴,∴点B的纵坐标为y1,点D的纵坐标为y2,∵点A在函数y=的图象上,点B在函数y=的图象上,且AB=,∴-=,∴y1=,同理y2=,又∵AB与CD间的距离为6,∴y1-
y2=-=6,解得a-b=3.
17.
【答案】6
【解析】如图,连接OE,CE,过点A作AF⊥x轴,过点D作DH⊥x轴,过点D作DG⊥AF,
∵过原点的直线与反比例函数y(k>0)的图象交于A,B两点,
∴A与B关于原点对称,
∴O是AB的中点,
∵BE⊥AE,
∴OE=OA,
∴∠OAE=∠AEO,
∵AE为∠BAC的平分线,
∴∠BAE=∠DAE,
∴∠DAE=∠AEO,
∴AD∥OE,
∴S△ACE=S△AOC,
∵AC=3DC,△ADE的面积为8,
∴S△ACE=S△AOC=12,
设点A(m,),
∵AC=3DC,DH∥AF,
∴3DH=AF,
∴D(3m,),
∵CH∥GD,AG∥DH,
∴△DHC∽△AGD,
∴S△HDCS△ADG,
∵S△AOC=S△AOF+S梯形AFHD+S△HDC(DH+AF)×FH+S△HDC2m12,
∴2k=12,∴k=6;
故答案为6.
三、解答题(本大题共4道小题)
18.
【答案】
(1)∵直线y=2x与反比例函数y=(k≠0,x>0)的图象交于点A(m,8),则2m=8,
解得m=4,
∴A(4,8),
∴k=4×8=32;
(2)设AC=x,则OC=x,BC=8-x,
在Rt△OBC中,由勾股定理得:OC2=OB2+BC2,
即x2=42+(8-x)2,解得x=5,∴AC=5;
(3)设点D的坐标为(x,0).分两种情况:
①当x>4时,如解图①,∵S△OCD=S△ACD,
∴OD·BC=AC·BD,
∴3x=5(x-4),解得x=10;
②当0<x<4时,如解图②,同理得:3x=5(4-x),解得x=.
∴点D的坐标为(10,0)或(,0).
19.
【答案】
解:(1)把A(4,1)代入y=得1=.
∴m=4,(2分)
∴反比例函数的解析式为y=.(3分)
(2)过点B作BE⊥y轴于点E,如解图,设点B坐标为(n,),则OE=,BE=n.
∴S△BEO=OE·BE=2,(4分)
∵S△BOC=3,
∴S△BCE=1,
∴OE∶EC=2∶1,
∴CE=,OC=.(6分)
设直线AB的解析式为y=kx+,把(n,)和(4,1)分别代入得:,
解得 ,(7分)
∴=3,
∴一次函数的解析式为y=-x+3.(8分)
20.
【答案】
解:(1)∵点A(2,-1)在反比例函数y=的图象上,
∴-1=,即m=-2.(1分)
∴反比例函数的解析式为y=-.(2分)
∵点B(,n)在反比例函数y=-的图象上,
∴n=-=-4,即点B的坐标为(,-4).
将点A(2,-1)和点B(,-4)分别代入y=kx+b,得
,解得,
∴一次函数的解析式为y=2x-5.(5分)
(2)如解图,设直线AB交y轴于点D.
令y=2x-5中x=0,得y=-5,即点D的坐标是(0,-5),
∴OD=5.(7分)
∵直线y=2与y轴交于点C,
∴C点的坐标是(0,2),(8分)
∴CD=OC+OD=7.
∴S△ABC=S△ACD-S△BCD=×7×2-×7×=7-=.(10分)
21.
【答案】
(1)反比例函数的解析式为y;(2)a的值为1或3.
【解析】(1)如图1,过点A作AC⊥OB于点C,
∵△OAB是等边三角形,
∴∠AOB=60°,OCOB,
∵B(4,0),
∴OB=OA=4,
∴OC=2,AC=2.
把点A(2,2)代入y,解得k=4.
∴反比例函数的解析式为y;
(2)分两种情况讨论:
①当点D是A′B′的中点,如图2,过点D作DE⊥x轴于点E.
由题意得A′B′=4,∠A′B′E=60°,
在Rt△DEB′中,B′D=2,DE=,B′E=1.
∴O′E=3,
把y代入y,得x=4,
∴OE=4,∴a=OO′=1;
②如图3,点F是A′O′的中点,过点F作FH⊥x轴于点H.
由题意得A′O′=4,∠A′O′B′=60°,
在Rt△FO′H中,FH,O′H=1.
把y代入y,得x=4,
∴OH=4,∴a=OO′=3,
综上所述,a的值为1或3.
