人教版九年级下册数学 27.1--27.3分节测试题(3小节 Word版 含答案)
文档属性
| 名称 | 人教版九年级下册数学 27.1--27.3分节测试题(3小节 Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 432.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 10:52:33 | ||
图片预览




文档简介
人教版九年级下册数学
27.1--27.3分节测试题含答案
27.1图形的相似
一、单选题
1.下列说法正确的是(
)
A.对应边都成比例的多边形相似
B.对应角都相等的多边形相似
C.边数相同的正多边形相似
D.矩形都相似
2.如图,分别是边上的点,,若,则的长是(
).
A.1
B.2
C.3
D.4
3.如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AC和BD相交于点E,EF⊥BD垂足为F.则下列结论错误的是( )
A.
B.
C.
D.
4.如图,有三个矩形,其中是相似图形的是(
)
A.甲和乙
B.甲和丙
C.乙和丙
D.甲、乙和丙
5.如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD∶DB=3∶5,那么CF∶CB等于(
)
A.5∶8
B.3∶8
C.3∶5
D.2∶5
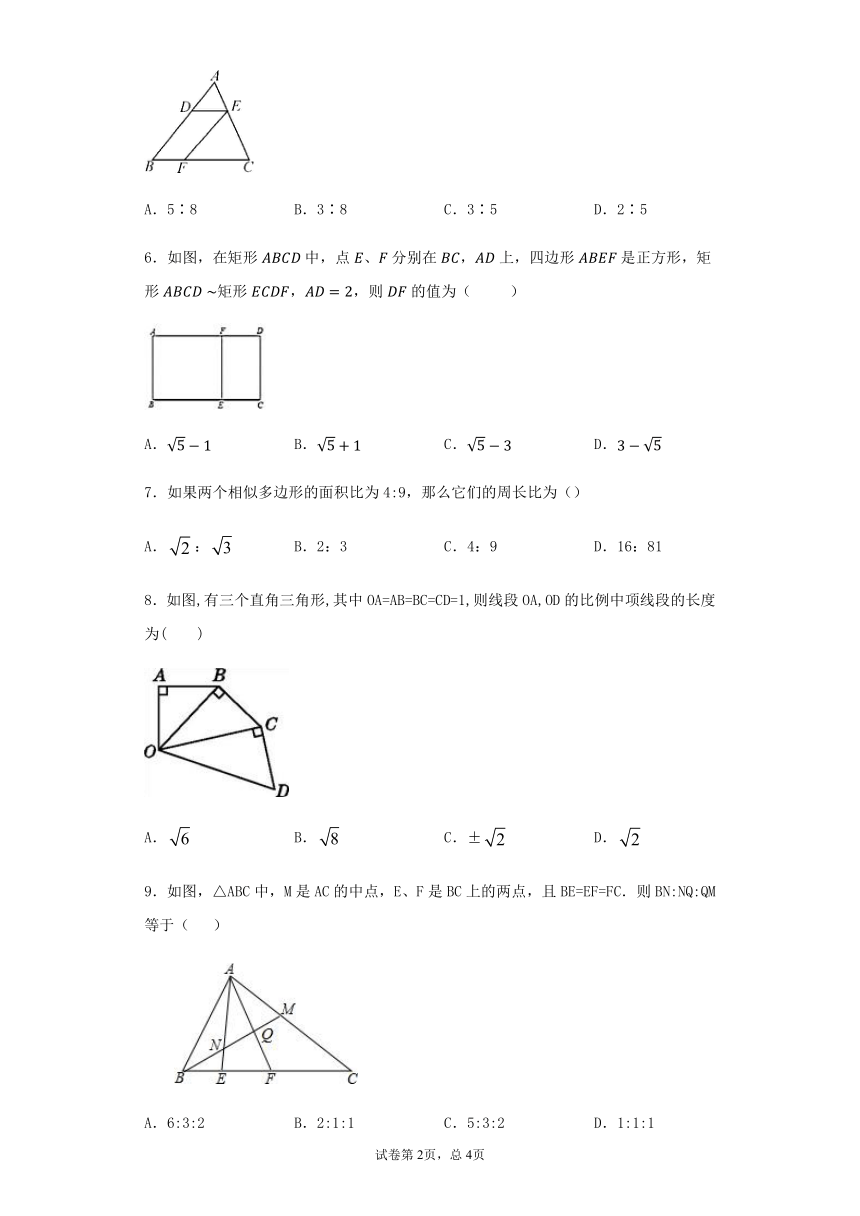
6.如图,在矩形中,点、分别在,上,四边形是正方形,矩形矩形,,则的值为(
)
A.
B.
C.
D.
7.如果两个相似多边形的面积比为4:9,那么它们的周长比为()
A.:
B.2:3
C.4:9
D.16:81
8.如图,有三个直角三角形,其中OA=AB=BC=CD=1,则线段OA,OD的比例中项线段的长度为( )
A.
B.
C.±
D.
9.如图,△ABC中,M是AC的中点,E、F是BC上的两点,且BE=EF=FC.则BN:NQ:QM等于(
)
A.6:3:2
B.2:1:1
C.5:3:2
D.1:1:1
二、填空题
10.已知线段a=2cm、b=8cm,那么线段a、b的比例中项等于_________cm..
11.如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若,AE=4,则EC等于_____.
12.已知AB∥CD,AD与BC相交于点O.若=,AD=10,则AO=____.
13.把一个正多边形放大到原来的2.5倍,则原图与新图的相似比为_____
14.在中,,点在直线上,,点为边的中点,连接,射线交于点,则的值为________.
15.小芳的房间有一面积为3?m2的玻璃窗,她站在室内离窗子4?m的地方向外看,她能看到窗前面一幢楼房的面积有____m2(楼之间的距离为20?m).
16.在长8cm,宽6cm的矩形中,截去一个矩形,使留下的矩形与原矩形相似,那么留下的矩形面积是_______cm2
17.如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D是AB的中点,E是直线BC上一点,把△BDE沿直线ED翻折后,点B落在点F处,当FD⊥BC时,线段BE的长为_____.
18.如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6.
P为对角线BD上一点,则PM—PN的最大值为___.
三、解答题
19.知四条线段的长度为
cm,
cm,
cm,
cm,判断它们是不是成比例线段.
20.如图,已知E是平行四边形ABCD中DA边的延长线上一点,且AD=2AE,连接EC分别交AB,BD于点F,G.
(1)求证:BF=2AF;
(2)若BD=20cm,求DG的长.
试卷第1页,总3页
试卷第1页,总3页
1.C
2.C
3.A
4.B
5.A
6.D
7.B
8.D
9.C
10.4
11.2
12.4.
13.
14.或
15.108
16.27
17.或5
18.2.
19.略
20.(1)略;(2)12cm.
27.2相似三角形
一、选择题
1、能判定与相似的条件是(??
)
A.???????????????
??
B.,且
C.且???
D.,且
2、已知两个相似三角形的周长比为4:9,则它们的面积比为(???
)
A.4:9??????
B.2:3????????
C.8:18???????
D.16:49
下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是(
)
A.??
B.??
C.??
D.
4、已知△ABC∽△A′B′C′,下列图形中,△ABC与△A′B′C′不存在位似关系的是( )
5、如图,在△ABC中,∠ADE
=
∠B,DE
:BC
=
2
:3,则下列结论正确的是(????
)
A.?
AD
:
AB
=
2
:
3;?????
B.AE
:
AC
=
2:5;???
C.
AD
:
DB
=
2
:
3;?????
D.CE
:
AE=
3
:
2.
6、如图,已知DE∥BC,那么下列结论正确的是( )
A.????
B.
C.????
D.
7、如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( )
A.??
B.????
C.????
D.
8、如图,在△ABC中,∠AED=∠B,DE=6,AB=10,AE=8,则BC的长度为(???
)
A. B. C.3 D.
9、如图,∠A=∠B=90°,AB=7,AD=2,BC=3,在边AB上取点P,使得△PAD与△PBC相似,则这样的P点共有( )
A.1个??
B.2个??
C.3个??
D.4个
10、如图所示,在河的一岸边选定一个目标A,再在河的另一岸边选定B和C,使AB⊥BC,然后选定E,使EC⊥BC,用视线确定BC和AE相交于D,此时测得BD=120米,CD=60米,为了估计河的宽度AB,还需要测量的线段是(??
)
A.CE?
B.DE
C.CE或DE?
D.无法确定
11、如图,,∠1=∠2,则对于结论:①△ABE∽△ACF;②△ABC∽△AEF;③;④.其中正确的结论的个数是( )
A.1????
B.2????
C.3????
D.4?????????????????????????????
12、如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为( )时,△ABE与以D、M、N为顶点的三角形相似
A.??
B.??????
C.或????
D.或
填空题
13、如图,在△ABC中,D、E分别是AB、AC边上的点(DE不平行于BC),当
时,△AED与△ABC相似.
14、如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是
.(只需写一个条件,不添加辅助线和字母)
?????
15、如图,在△ABC
中,D.
E
分别是
AB、AC
边的中点,则的值为
16、如图,两条直线被第三条直线所截,DE=,EF=,AB=1,则AC= ??
.
17、如图,在△ABC
中,∠C=90°,BC=6,D,E分别在AB、AC
上,将△ABC沿DE折叠,使点A落在点处,若为CE的中点,则折痕DE的长为 ??
.
18、在边长为2cm的正方形ABCD中,动点E、F分别从D、C两点同时出发,都以1cm/s的速度在射线DC、CB上移动.连接AE和DF交于点P,点Q为AD的中点.若以A、P、Q为顶点的三角形与以P、D、C为顶点的三角形相似,则运动时间t为
秒.
三、简答题
19、?在△ABC中,AB=12,点E在AC上,点D在AB上,若AE=6,EC=4,。
(1)求AD的长;
(2)试问能成立吗?请说明理由。
20、如图,△ABC内接于⊙O,过C作CD∥AB与⊙O相交于D点,E是上一点,且满足AD=DE,连接BD与AE相交于点F.求证:△ADF∽△ABC.
21、周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
22、如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB?AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求的值.
23、如图,一次函数y=kx+b(k,b为常数,且k≠0)的图象与x轴,y轴分别交于A,B两点,且与反比例函数y=(n为常数,且n≠0)的图象在第二象限交于点C,CD⊥x轴,垂足为点D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤的解集.
24、感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)
探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6,CE=4,则DE的长为 ??
.
参考答案
一、选择题
1、.C;2、D;3、.B;4、D;5、A;6、B;7、B;8、A;9、C;10、C;11、B;12、C;
二、填空题
13、 不唯一,如∠ADE=∠C
14、AB∥DE .
15、
16、+1.
17、2
18、2或4
三、简答题
19、1)设AD=x,则BD=AB-AD=(12-x)cm,根据比例式列出方程求得x的值,即可得AD的长;(2)根据所求得的数据计算即可得结论.
解:(1)设AD=x,则BD=AB-AD=(12-x)cm,
x:12-x=6:4,解得x=7.2,
∴AD=7.2;
(2)能,
由AB=12,AD=,故DB=.
于是,
又,故.
20、?证明:∵AB∥CD,∴∠BAC=∠ACD,∵AD=DE,∴∠DAE=∠AED,∴∠DAE=∠AED=∠ACD=∠BAC,∵∠ADF=∠ACB,∠DAE=∠BAC,∴△ADF∽△ABC.
21、【解答】解:∵BC∥DE,
∴△ABC∽△ADE,
∴=,
∴=,
∴AB=17(m),
经检验:AB=17是分式方程的解,
答:河宽AB的长为17米.
22、(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB?AD;
(2)证明:∵E为AB的中点,
∴CE=AB=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
(3)解:∵CE∥AD,
∴△AFD∽△CFE,
∴AD:CE=AF:CF,
∵CE=AB,
∴CE=×6=3,
∵AD=4,
∴,
∴.
23、(1)代入y=-2x+12中,
(2)140.
(3)不等式kx+b≤的解集为x≥10或-4≤x<0.
24、解:感知:∵∠APD=90°,
∴∠APB+∠DPC=90°,
∵∠B=90°,
∴∠APB+∠BAP=90°,
∴∠BAP=∠DPC,
∵AB∥CD,∠B=90°,
∴∠C=∠B=90°,
∴△ABP∽△PCD.
探究:∵∠APC=∠BAP+∠B,∠APC=∠APD+∠CPD,
∴∠BAP+∠B=∠APD+∠CPD.
∵∠B=∠APD,
∴∠BAP=∠CPD.
∵∠B=∠C,
∴△ABP∽△PCD,
拓展:同探究的方法得出,△BDP∽△CPE,
∴,
∵点P是边BC的中点,
∴BP=CP=3,
∵CE=4,
∴,
∴BD=,
∵∠B=∠C=45°,
∴∠A=180°﹣∠B﹣∠C=90°,
即AC⊥AB且AC=AB=6,
∴AD=AB﹣BD=6﹣=,AE=AC﹣CE=6﹣4=2,
在Rt△ADE中,DE===.
《27.3 位似》
一、基础题
1.两个位似图形中,对应点到位似中心的距离之比为2∶3,则这两个图形的相似比为(
)
A.4∶9
B.2∶3
C.
1∶2
D.
∶
2.如图,△ABC与△DEF是位似图形,相似比为2∶3,已知AB=4,则DE的长等于(
)
A.9
B.5
C.6
D.
3.如图,两个三角形是位似图形,它们的位似中心是(
)
A.点P
B.点O
C.点M
D.点N
4.下列关于位似图形的表述:
①相似图形一定是位似图形,位似图形一定是相似图形
②位似图形一定有位似中心
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形
④位似图形上任意两点与位似中心的距离之比等于相似比.
其中正确命题的序号是(
)
A.②③
B.①②
C.③④
D.②③④
5.视力表的一部分如图,其中开口向上的两个“E”之间的变换是(
)
A.位似
B.旋转
C.对称
D.平移
6.已知:△ABC∽△A′B′C′,下列图形中,△ABC与△A′B′C′不存在位似关系的是(
)
7.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA∶OA′=2∶3,则四边形ABCD与四边形A′B′C′D′的面积比为(
)
A.4∶9
B.2∶5
C.2∶3
D.∶
8.如图,已知△ABC,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是(
)
①△ABC与△DEF是位似图形
②△ABC与△DEF是相似图形
③△ABC与△DEF的周长比为1∶2
④△ABC与△DEF的面积比为4∶1.
A.4
B.3
C.2
D.1
9.如图,以O为位似中心,将四边形ABCD缩小为原来的一半.
二、提升题
10.如图,已知BC∥DE,则下列说法中不正确的是(
)
A.∠ADE=∠B
B.点A是两个三角形的位似中心
C.两个三角形是位似图形
D.点B与点E,点C与点D是对应点
11.如图,四边形ABCD与四边形AEFG是位似图形,且AC∶AF=2∶3,则下列结论不正确的是(
)
A.AD与AE的比是2∶3
B.四边形ABCD与四边形AEFG是相似图形
C.四边形ABCD与四边形AEFG的周长比是2∶3
D.四边形ABCD与四边形AEFG的面积比是4∶9
12.如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为20
cm,到屏幕的距离为60
cm,且幻灯片中图形的高度为6
cm,则屏幕上图形的高度为
.
13.如图,以O为位似中心,将边长为256的正方形OABC依次作位似变换,经第一次变化后得正方形OA1B1C1,其边长OA1缩小为OA的,经第二次变化后得正方形OA2B2C2,其边长OA2缩小为OA1的,经第三次变化后得正方形OA3B3C3,其边长OA3缩小为OA2的,…,依此规律,经第n次变化后,所得正方形OAnBnCn的边长为正方形OABC边长的倒数,则n=
.
14.如图,△ABC与△A′B′C′是位似图形,且相似比是1∶2,若AB=2
cm,则A′B′=
cm,并在图中画出位似中心O.
15.如图,已知△DEO与△ABO是位似图形,△OEF与△OBC是位似图形,求证:OD·OC=OF·OA.
16.如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2.
(1)将△ABC向右平移4个单位长度,再向上平移1个单位长度,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
参考答案
一、基础题
1.B
2.C
3.A
4.A
5.A
6.D
7.A
8.B
9.略.
二、提升题
10.D
11.A
12.18cm
13.16
14.4
解:如图所示.
15.证明:∵△DEO与△ABO位似,
∴=.
∵△OEF与△OBC位似,
∴=.
∴=.
∴OD·OC=OF·OA.
16.解:如图.
27.1--27.3分节测试题含答案
27.1图形的相似
一、单选题
1.下列说法正确的是(
)
A.对应边都成比例的多边形相似
B.对应角都相等的多边形相似
C.边数相同的正多边形相似
D.矩形都相似
2.如图,分别是边上的点,,若,则的长是(
).
A.1
B.2
C.3
D.4
3.如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AC和BD相交于点E,EF⊥BD垂足为F.则下列结论错误的是( )
A.
B.
C.
D.
4.如图,有三个矩形,其中是相似图形的是(
)
A.甲和乙
B.甲和丙
C.乙和丙
D.甲、乙和丙
5.如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD∶DB=3∶5,那么CF∶CB等于(
)
A.5∶8
B.3∶8
C.3∶5
D.2∶5
6.如图,在矩形中,点、分别在,上,四边形是正方形,矩形矩形,,则的值为(
)
A.
B.
C.
D.
7.如果两个相似多边形的面积比为4:9,那么它们的周长比为()
A.:
B.2:3
C.4:9
D.16:81
8.如图,有三个直角三角形,其中OA=AB=BC=CD=1,则线段OA,OD的比例中项线段的长度为( )
A.
B.
C.±
D.
9.如图,△ABC中,M是AC的中点,E、F是BC上的两点,且BE=EF=FC.则BN:NQ:QM等于(
)
A.6:3:2
B.2:1:1
C.5:3:2
D.1:1:1
二、填空题
10.已知线段a=2cm、b=8cm,那么线段a、b的比例中项等于_________cm..
11.如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若,AE=4,则EC等于_____.
12.已知AB∥CD,AD与BC相交于点O.若=,AD=10,则AO=____.
13.把一个正多边形放大到原来的2.5倍,则原图与新图的相似比为_____
14.在中,,点在直线上,,点为边的中点,连接,射线交于点,则的值为________.
15.小芳的房间有一面积为3?m2的玻璃窗,她站在室内离窗子4?m的地方向外看,她能看到窗前面一幢楼房的面积有____m2(楼之间的距离为20?m).
16.在长8cm,宽6cm的矩形中,截去一个矩形,使留下的矩形与原矩形相似,那么留下的矩形面积是_______cm2
17.如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D是AB的中点,E是直线BC上一点,把△BDE沿直线ED翻折后,点B落在点F处,当FD⊥BC时,线段BE的长为_____.
18.如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6.
P为对角线BD上一点,则PM—PN的最大值为___.
三、解答题
19.知四条线段的长度为
cm,
cm,
cm,
cm,判断它们是不是成比例线段.
20.如图,已知E是平行四边形ABCD中DA边的延长线上一点,且AD=2AE,连接EC分别交AB,BD于点F,G.
(1)求证:BF=2AF;
(2)若BD=20cm,求DG的长.
试卷第1页,总3页
试卷第1页,总3页
1.C
2.C
3.A
4.B
5.A
6.D
7.B
8.D
9.C
10.4
11.2
12.4.
13.
14.或
15.108
16.27
17.或5
18.2.
19.略
20.(1)略;(2)12cm.
27.2相似三角形
一、选择题
1、能判定与相似的条件是(??
)
A.???????????????
??
B.,且
C.且???
D.,且
2、已知两个相似三角形的周长比为4:9,则它们的面积比为(???
)
A.4:9??????
B.2:3????????
C.8:18???????
D.16:49
下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是(
)
A.??
B.??
C.??
D.
4、已知△ABC∽△A′B′C′,下列图形中,△ABC与△A′B′C′不存在位似关系的是( )
5、如图,在△ABC中,∠ADE
=
∠B,DE
:BC
=
2
:3,则下列结论正确的是(????
)
A.?
AD
:
AB
=
2
:
3;?????
B.AE
:
AC
=
2:5;???
C.
AD
:
DB
=
2
:
3;?????
D.CE
:
AE=
3
:
2.
6、如图,已知DE∥BC,那么下列结论正确的是( )
A.????
B.
C.????
D.
7、如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( )
A.??
B.????
C.????
D.
8、如图,在△ABC中,∠AED=∠B,DE=6,AB=10,AE=8,则BC的长度为(???
)
A. B. C.3 D.
9、如图,∠A=∠B=90°,AB=7,AD=2,BC=3,在边AB上取点P,使得△PAD与△PBC相似,则这样的P点共有( )
A.1个??
B.2个??
C.3个??
D.4个
10、如图所示,在河的一岸边选定一个目标A,再在河的另一岸边选定B和C,使AB⊥BC,然后选定E,使EC⊥BC,用视线确定BC和AE相交于D,此时测得BD=120米,CD=60米,为了估计河的宽度AB,还需要测量的线段是(??
)
A.CE?
B.DE
C.CE或DE?
D.无法确定
11、如图,,∠1=∠2,则对于结论:①△ABE∽△ACF;②△ABC∽△AEF;③;④.其中正确的结论的个数是( )
A.1????
B.2????
C.3????
D.4?????????????????????????????
12、如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为( )时,△ABE与以D、M、N为顶点的三角形相似
A.??
B.??????
C.或????
D.或
填空题
13、如图,在△ABC中,D、E分别是AB、AC边上的点(DE不平行于BC),当
时,△AED与△ABC相似.
14、如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是
.(只需写一个条件,不添加辅助线和字母)
?????
15、如图,在△ABC
中,D.
E
分别是
AB、AC
边的中点,则的值为
16、如图,两条直线被第三条直线所截,DE=,EF=,AB=1,则AC= ??
.
17、如图,在△ABC
中,∠C=90°,BC=6,D,E分别在AB、AC
上,将△ABC沿DE折叠,使点A落在点处,若为CE的中点,则折痕DE的长为 ??
.
18、在边长为2cm的正方形ABCD中,动点E、F分别从D、C两点同时出发,都以1cm/s的速度在射线DC、CB上移动.连接AE和DF交于点P,点Q为AD的中点.若以A、P、Q为顶点的三角形与以P、D、C为顶点的三角形相似,则运动时间t为
秒.
三、简答题
19、?在△ABC中,AB=12,点E在AC上,点D在AB上,若AE=6,EC=4,。
(1)求AD的长;
(2)试问能成立吗?请说明理由。
20、如图,△ABC内接于⊙O,过C作CD∥AB与⊙O相交于D点,E是上一点,且满足AD=DE,连接BD与AE相交于点F.求证:△ADF∽△ABC.
21、周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
22、如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB?AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求的值.
23、如图,一次函数y=kx+b(k,b为常数,且k≠0)的图象与x轴,y轴分别交于A,B两点,且与反比例函数y=(n为常数,且n≠0)的图象在第二象限交于点C,CD⊥x轴,垂足为点D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤的解集.
24、感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)
探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6,CE=4,则DE的长为 ??
.
参考答案
一、选择题
1、.C;2、D;3、.B;4、D;5、A;6、B;7、B;8、A;9、C;10、C;11、B;12、C;
二、填空题
13、 不唯一,如∠ADE=∠C
14、AB∥DE .
15、
16、+1.
17、2
18、2或4
三、简答题
19、1)设AD=x,则BD=AB-AD=(12-x)cm,根据比例式列出方程求得x的值,即可得AD的长;(2)根据所求得的数据计算即可得结论.
解:(1)设AD=x,则BD=AB-AD=(12-x)cm,
x:12-x=6:4,解得x=7.2,
∴AD=7.2;
(2)能,
由AB=12,AD=,故DB=.
于是,
又,故.
20、?证明:∵AB∥CD,∴∠BAC=∠ACD,∵AD=DE,∴∠DAE=∠AED,∴∠DAE=∠AED=∠ACD=∠BAC,∵∠ADF=∠ACB,∠DAE=∠BAC,∴△ADF∽△ABC.
21、【解答】解:∵BC∥DE,
∴△ABC∽△ADE,
∴=,
∴=,
∴AB=17(m),
经检验:AB=17是分式方程的解,
答:河宽AB的长为17米.
22、(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB?AD;
(2)证明:∵E为AB的中点,
∴CE=AB=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
(3)解:∵CE∥AD,
∴△AFD∽△CFE,
∴AD:CE=AF:CF,
∵CE=AB,
∴CE=×6=3,
∵AD=4,
∴,
∴.
23、(1)代入y=-2x+12中,
(2)140.
(3)不等式kx+b≤的解集为x≥10或-4≤x<0.
24、解:感知:∵∠APD=90°,
∴∠APB+∠DPC=90°,
∵∠B=90°,
∴∠APB+∠BAP=90°,
∴∠BAP=∠DPC,
∵AB∥CD,∠B=90°,
∴∠C=∠B=90°,
∴△ABP∽△PCD.
探究:∵∠APC=∠BAP+∠B,∠APC=∠APD+∠CPD,
∴∠BAP+∠B=∠APD+∠CPD.
∵∠B=∠APD,
∴∠BAP=∠CPD.
∵∠B=∠C,
∴△ABP∽△PCD,
拓展:同探究的方法得出,△BDP∽△CPE,
∴,
∵点P是边BC的中点,
∴BP=CP=3,
∵CE=4,
∴,
∴BD=,
∵∠B=∠C=45°,
∴∠A=180°﹣∠B﹣∠C=90°,
即AC⊥AB且AC=AB=6,
∴AD=AB﹣BD=6﹣=,AE=AC﹣CE=6﹣4=2,
在Rt△ADE中,DE===.
《27.3 位似》
一、基础题
1.两个位似图形中,对应点到位似中心的距离之比为2∶3,则这两个图形的相似比为(
)
A.4∶9
B.2∶3
C.
1∶2
D.
∶
2.如图,△ABC与△DEF是位似图形,相似比为2∶3,已知AB=4,则DE的长等于(
)
A.9
B.5
C.6
D.
3.如图,两个三角形是位似图形,它们的位似中心是(
)
A.点P
B.点O
C.点M
D.点N
4.下列关于位似图形的表述:
①相似图形一定是位似图形,位似图形一定是相似图形
②位似图形一定有位似中心
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形
④位似图形上任意两点与位似中心的距离之比等于相似比.
其中正确命题的序号是(
)
A.②③
B.①②
C.③④
D.②③④
5.视力表的一部分如图,其中开口向上的两个“E”之间的变换是(
)
A.位似
B.旋转
C.对称
D.平移
6.已知:△ABC∽△A′B′C′,下列图形中,△ABC与△A′B′C′不存在位似关系的是(
)
7.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA∶OA′=2∶3,则四边形ABCD与四边形A′B′C′D′的面积比为(
)
A.4∶9
B.2∶5
C.2∶3
D.∶
8.如图,已知△ABC,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是(
)
①△ABC与△DEF是位似图形
②△ABC与△DEF是相似图形
③△ABC与△DEF的周长比为1∶2
④△ABC与△DEF的面积比为4∶1.
A.4
B.3
C.2
D.1
9.如图,以O为位似中心,将四边形ABCD缩小为原来的一半.
二、提升题
10.如图,已知BC∥DE,则下列说法中不正确的是(
)
A.∠ADE=∠B
B.点A是两个三角形的位似中心
C.两个三角形是位似图形
D.点B与点E,点C与点D是对应点
11.如图,四边形ABCD与四边形AEFG是位似图形,且AC∶AF=2∶3,则下列结论不正确的是(
)
A.AD与AE的比是2∶3
B.四边形ABCD与四边形AEFG是相似图形
C.四边形ABCD与四边形AEFG的周长比是2∶3
D.四边形ABCD与四边形AEFG的面积比是4∶9
12.如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为20
cm,到屏幕的距离为60
cm,且幻灯片中图形的高度为6
cm,则屏幕上图形的高度为
.
13.如图,以O为位似中心,将边长为256的正方形OABC依次作位似变换,经第一次变化后得正方形OA1B1C1,其边长OA1缩小为OA的,经第二次变化后得正方形OA2B2C2,其边长OA2缩小为OA1的,经第三次变化后得正方形OA3B3C3,其边长OA3缩小为OA2的,…,依此规律,经第n次变化后,所得正方形OAnBnCn的边长为正方形OABC边长的倒数,则n=
.
14.如图,△ABC与△A′B′C′是位似图形,且相似比是1∶2,若AB=2
cm,则A′B′=
cm,并在图中画出位似中心O.
15.如图,已知△DEO与△ABO是位似图形,△OEF与△OBC是位似图形,求证:OD·OC=OF·OA.
16.如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2.
(1)将△ABC向右平移4个单位长度,再向上平移1个单位长度,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
参考答案
一、基础题
1.B
2.C
3.A
4.A
5.A
6.D
7.A
8.B
9.略.
二、提升题
10.D
11.A
12.18cm
13.16
14.4
解:如图所示.
15.证明:∵△DEO与△ABO位似,
∴=.
∵△OEF与△OBC位似,
∴=.
∴=.
∴OD·OC=OF·OA.
16.解:如图.
