北师大版九年级数学下册 2.3 确定二次函数的表达式 同步测试题(word版,含答案)
文档属性
| 名称 | 北师大版九年级数学下册 2.3 确定二次函数的表达式 同步测试题(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 30.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 10:59:48 | ||
图片预览



文档简介
2.3
确定二次函数的表达式
同步测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
如果抛物线经过点,和,则的值为(
)
A.
B.
C.
D.
?
2.
抛物线=经过点和,且以直线=为对称轴,则它的解析式为(
)
A.=
B.=
C.=
D.=
?
3.
将二次函数化为的形式,下列结果正确的是(?
?
?
?
)
A.
B.
C.
D.
?
4.
已知二次函数的图象经过点,顶点坐标为,则此二次函数的解析式为?
?
?
?
A.
B.
C.
D.
?
5.
将函数变形为的形式,正确的是(
)
A.
B.
C.
D.
?
6.
若二次函数配方后为,则,的值分别(
)
A.,
B.,
C.,
D.,
?
7.
若某抛物线的顶点坐标为且经过点,则该抛物线的表达式为(?
?
?
?
)
A.
B.
C.
D.
?8.
抛物线与轴交于点和,且与交于点,则该抛物线的解析式为(
)
A.
B.
C.
D.
?
9.
已知抛物线过点,,与轴交于点,且.则这条抛物线的解析式为(
)
A.
B.
C.或
D.或
?10.
把二次函数通过配方,化成的形式,正确的是(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
把写成的形式为________.
?
12.
二次函数的图象过,则它的解析式为________,当________时,随着的增大而减小.
?
13.
抛物线和形状相同,方向相反,且顶点为,则它的关系式为________.
?
14.
把二次函数改写成的形式是________,其顶点坐标是________.
?
15.
已知一抛物线和的图象形状相同,对称轴平行于轴,且顶点坐标为,则它所对应的函数关系式为________.
?
16.
已知二次函数的图象开口向下,且与轴的正半轴相交.请你写出一个满足条件的二次函数的解析式:________.
?17.
抛物线经过,两点,则这条抛物线的解析式为________.
?
18.
若二次函数的图象经过点,则二次函数的解析式是________.
?
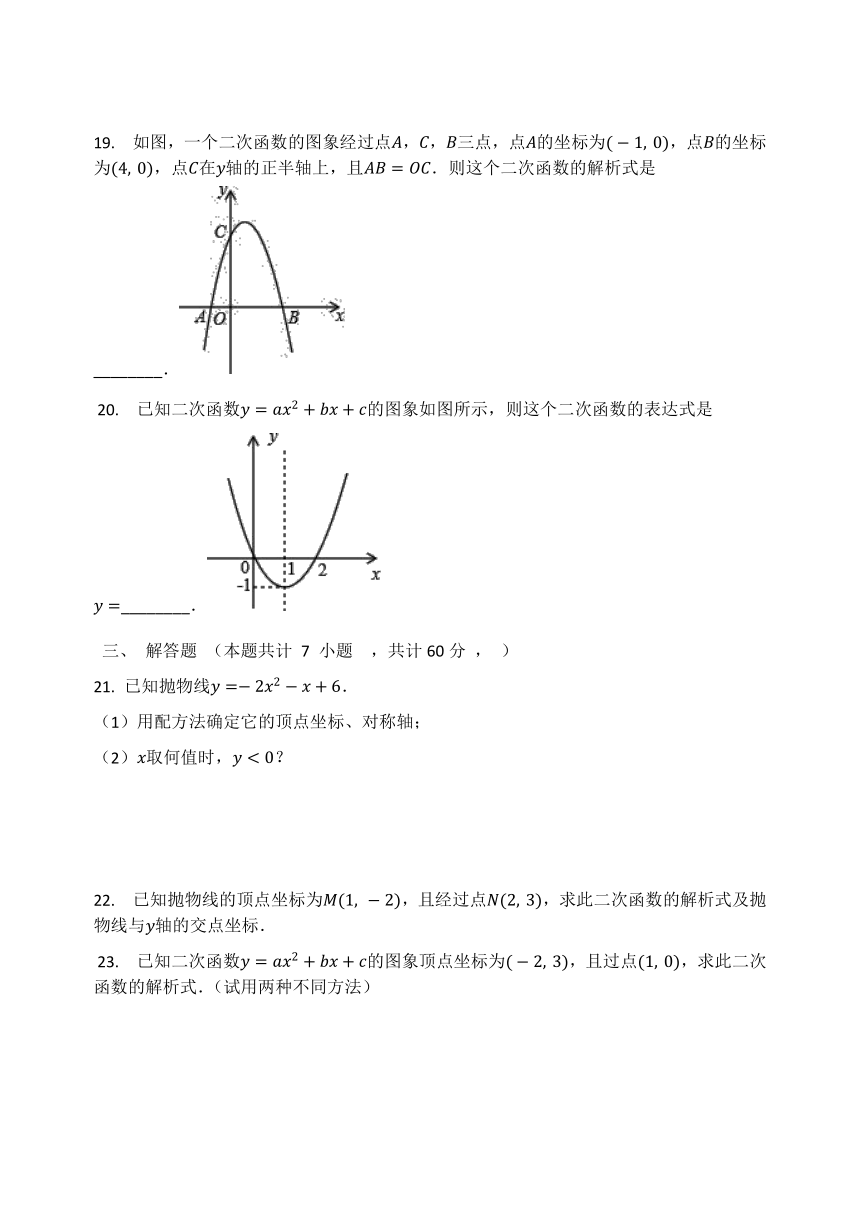
19.
如图,一个二次函数的图象经过点,,三点,点的坐标为,点的坐标为,点在轴的正半轴上,且.则这个二次函数的解析式是________.
?20.
已知二次函数的图象如图所示,则这个二次函数的表达式是________.
三、
解答题
(本题共计
7
小题
,共计60分
,
)
?
21.
已知抛物线.
(1)用配方法确定它的顶点坐标、对称轴;
(2)取何值时,?
?
22.
已知抛物线的顶点坐标为,且经过点,求此二次函数的解析式及抛物线与轴的交点坐标.
?23.
已知二次函数的图象顶点坐标为,且过点,求此二次函数的解析式.(试用两种不同方法)
?
24.
已知二次函数,如果,且当时,,那么当时,的值是多少?
?
25.
已知抛物线.变换式子,指出抛物线的开口方向、对称轴和顶点坐标.
?
26.
已知抛物线经过,,三点.
(1)求这条抛物线的表达式.
(2)写出抛物线的开口方向、对称轴和顶点坐标.
?
27.
已知抛物线与轴交于,,与轴负半轴交于点,,求抛物线解析式.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
C
2.
【答案】
B
3.
【答案】
C
4.
【答案】
A
5.
【答案】
C
6.
【答案】
B
7.
【答案】
A
8.
【答案】
D
9.
【答案】
C
10.
【答案】
C
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
12.
【答案】
,
13.
【答案】
﹢
14.
【答案】
,
15.
【答案】
或
16.
【答案】
=,=等,答案不唯一
17.
【答案】
18.
【答案】
19.
【答案】
20.
【答案】
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
21.
【答案】
解:(1),
顶点坐标,
对称轴是直线;??????
(2)令,即,
解得或,
∵
抛物线开口向下,
∴
当或时,.
22.
【答案】
解:设过顶点,得:
∵
经过点,
∴
,
∴
,
∴
,
当时,
∴
抛物线与轴的交点坐标为.
23.
【答案】
解:方法∵
二次函数的顶点坐标为,
二次函数中,图象的顶点坐标为,
∴
,,
又∵
过点,
∴
,
∴
根据题意得,
解得,,
∴
这个二次函数的解析式为;
24.
【答案】
解:把,代入得,
∵
,
∴
,,
∴
当时,.
25.
【答案】
解:
,
,
,
∴
抛物线的开口方向向上、对称轴为,顶点坐标为:.
26.
【答案】
解:(1)由题意得,
解得.
所以这个抛物线的表达式为.
(2),
所以抛物线的开口向上,对称轴为,顶点坐标为
27.
【答案】
解:将、、代入解析式得,
解得:.
则二次函数解析式为.
确定二次函数的表达式
同步测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
如果抛物线经过点,和,则的值为(
)
A.
B.
C.
D.
?
2.
抛物线=经过点和,且以直线=为对称轴,则它的解析式为(
)
A.=
B.=
C.=
D.=
?
3.
将二次函数化为的形式,下列结果正确的是(?
?
?
?
)
A.
B.
C.
D.
?
4.
已知二次函数的图象经过点,顶点坐标为,则此二次函数的解析式为?
?
?
?
A.
B.
C.
D.
?
5.
将函数变形为的形式,正确的是(
)
A.
B.
C.
D.
?
6.
若二次函数配方后为,则,的值分别(
)
A.,
B.,
C.,
D.,
?
7.
若某抛物线的顶点坐标为且经过点,则该抛物线的表达式为(?
?
?
?
)
A.
B.
C.
D.
?8.
抛物线与轴交于点和,且与交于点,则该抛物线的解析式为(
)
A.
B.
C.
D.
?
9.
已知抛物线过点,,与轴交于点,且.则这条抛物线的解析式为(
)
A.
B.
C.或
D.或
?10.
把二次函数通过配方,化成的形式,正确的是(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
把写成的形式为________.
?
12.
二次函数的图象过,则它的解析式为________,当________时,随着的增大而减小.
?
13.
抛物线和形状相同,方向相反,且顶点为,则它的关系式为________.
?
14.
把二次函数改写成的形式是________,其顶点坐标是________.
?
15.
已知一抛物线和的图象形状相同,对称轴平行于轴,且顶点坐标为,则它所对应的函数关系式为________.
?
16.
已知二次函数的图象开口向下,且与轴的正半轴相交.请你写出一个满足条件的二次函数的解析式:________.
?17.
抛物线经过,两点,则这条抛物线的解析式为________.
?
18.
若二次函数的图象经过点,则二次函数的解析式是________.
?
19.
如图,一个二次函数的图象经过点,,三点,点的坐标为,点的坐标为,点在轴的正半轴上,且.则这个二次函数的解析式是________.
?20.
已知二次函数的图象如图所示,则这个二次函数的表达式是________.
三、
解答题
(本题共计
7
小题
,共计60分
,
)
?
21.
已知抛物线.
(1)用配方法确定它的顶点坐标、对称轴;
(2)取何值时,?
?
22.
已知抛物线的顶点坐标为,且经过点,求此二次函数的解析式及抛物线与轴的交点坐标.
?23.
已知二次函数的图象顶点坐标为,且过点,求此二次函数的解析式.(试用两种不同方法)
?
24.
已知二次函数,如果,且当时,,那么当时,的值是多少?
?
25.
已知抛物线.变换式子,指出抛物线的开口方向、对称轴和顶点坐标.
?
26.
已知抛物线经过,,三点.
(1)求这条抛物线的表达式.
(2)写出抛物线的开口方向、对称轴和顶点坐标.
?
27.
已知抛物线与轴交于,,与轴负半轴交于点,,求抛物线解析式.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
C
2.
【答案】
B
3.
【答案】
C
4.
【答案】
A
5.
【答案】
C
6.
【答案】
B
7.
【答案】
A
8.
【答案】
D
9.
【答案】
C
10.
【答案】
C
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
12.
【答案】
,
13.
【答案】
﹢
14.
【答案】
,
15.
【答案】
或
16.
【答案】
=,=等,答案不唯一
17.
【答案】
18.
【答案】
19.
【答案】
20.
【答案】
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
21.
【答案】
解:(1),
顶点坐标,
对称轴是直线;??????
(2)令,即,
解得或,
∵
抛物线开口向下,
∴
当或时,.
22.
【答案】
解:设过顶点,得:
∵
经过点,
∴
,
∴
,
∴
,
当时,
∴
抛物线与轴的交点坐标为.
23.
【答案】
解:方法∵
二次函数的顶点坐标为,
二次函数中,图象的顶点坐标为,
∴
,,
又∵
过点,
∴
,
∴
根据题意得,
解得,,
∴
这个二次函数的解析式为;
24.
【答案】
解:把,代入得,
∵
,
∴
,,
∴
当时,.
25.
【答案】
解:
,
,
,
∴
抛物线的开口方向向上、对称轴为,顶点坐标为:.
26.
【答案】
解:(1)由题意得,
解得.
所以这个抛物线的表达式为.
(2),
所以抛物线的开口向上,对称轴为,顶点坐标为
27.
【答案】
解:将、、代入解析式得,
解得:.
则二次函数解析式为.
