人教版数学八年级上册第十三章 13.1 轴对称培优练习(word解析版)
文档属性
| 名称 | 人教版数学八年级上册第十三章 13.1 轴对称培优练习(word解析版) | 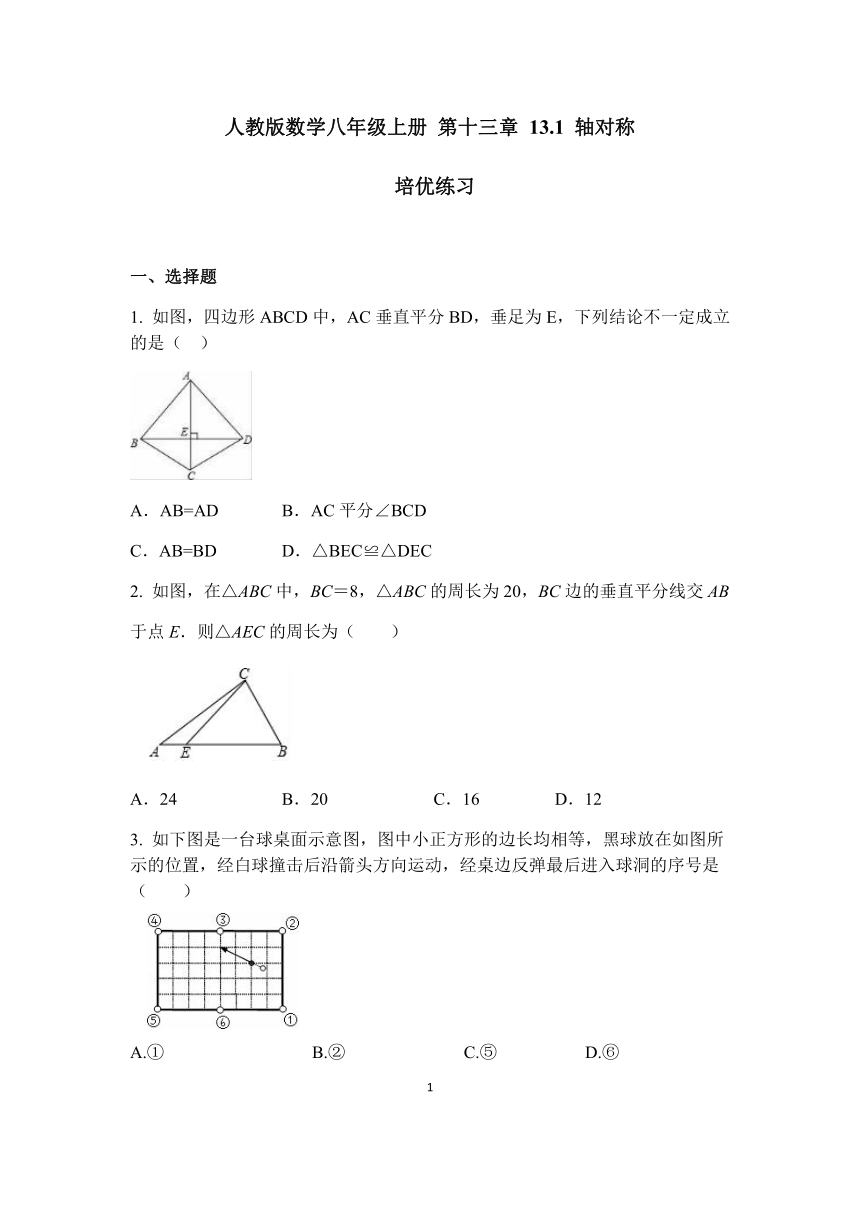 | |
| 格式 | zip | ||
| 文件大小 | 302.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 11:30:36 | ||
图片预览



文档简介
人教版数学八年级上册
第十三章
13.1
轴对称
培优练习
一、选择题
1.
如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是(
)
A.AB=AD
B.AC平分∠BCD
C.AB=BD
D.△BEC≌△DEC
2.
如图,在△ABC中,BC=8,△ABC的周长为20,BC边的垂直平分线交AB
于点E.则△AEC的周长为( )
A.24
B.20
C.16
D.12
3.
如下图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
A.①???
?
B.②???
?
C.⑤???
?
D.⑥
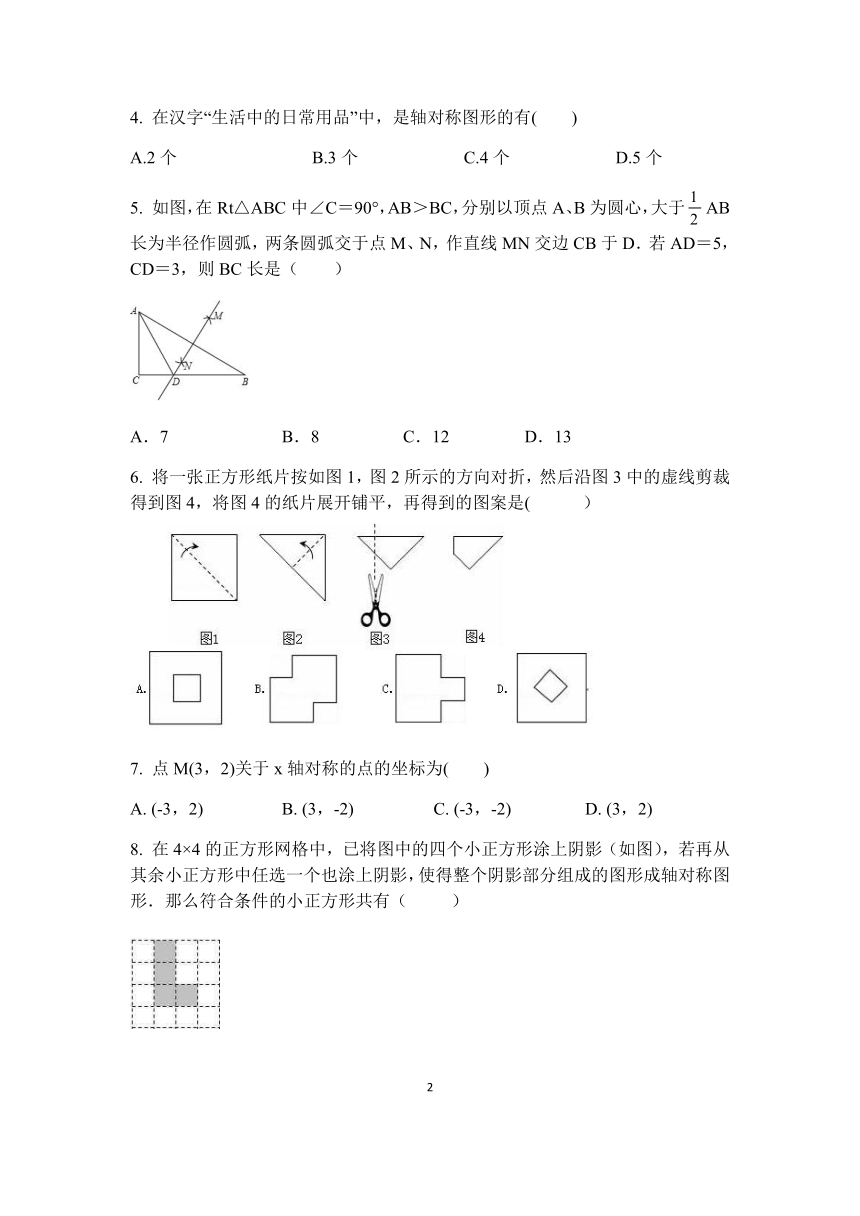
4.
在汉字“生活中的日常用品”中,是轴对称图形的有( )
A.2个
B.3个
C.4个
D.5个
5.
如图,在Rt△ABC中∠C=90°,AB>BC,分别以顶点A、B为圆心,大于AB长为半径作圆弧,两条圆弧交于点M、N,作直线MN交边CB于D.若AD=5,CD=3,则BC长是(
)
A.7
B.8
C.12
D.13
6.
将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图4,将图4的纸片展开铺平,再得到的图案是(
)
7.
点M(3,2)关于x轴对称的点的坐标为( )
A.
(-3,2)
B.
(3,-2)
C.
(-3,-2)
D.
(3,2)
8.
在4×4的正方形网格中,已将图中的四个小正方形涂上阴影(如图),若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有(
)
A.1个
B.2个
C.3个
D.4个
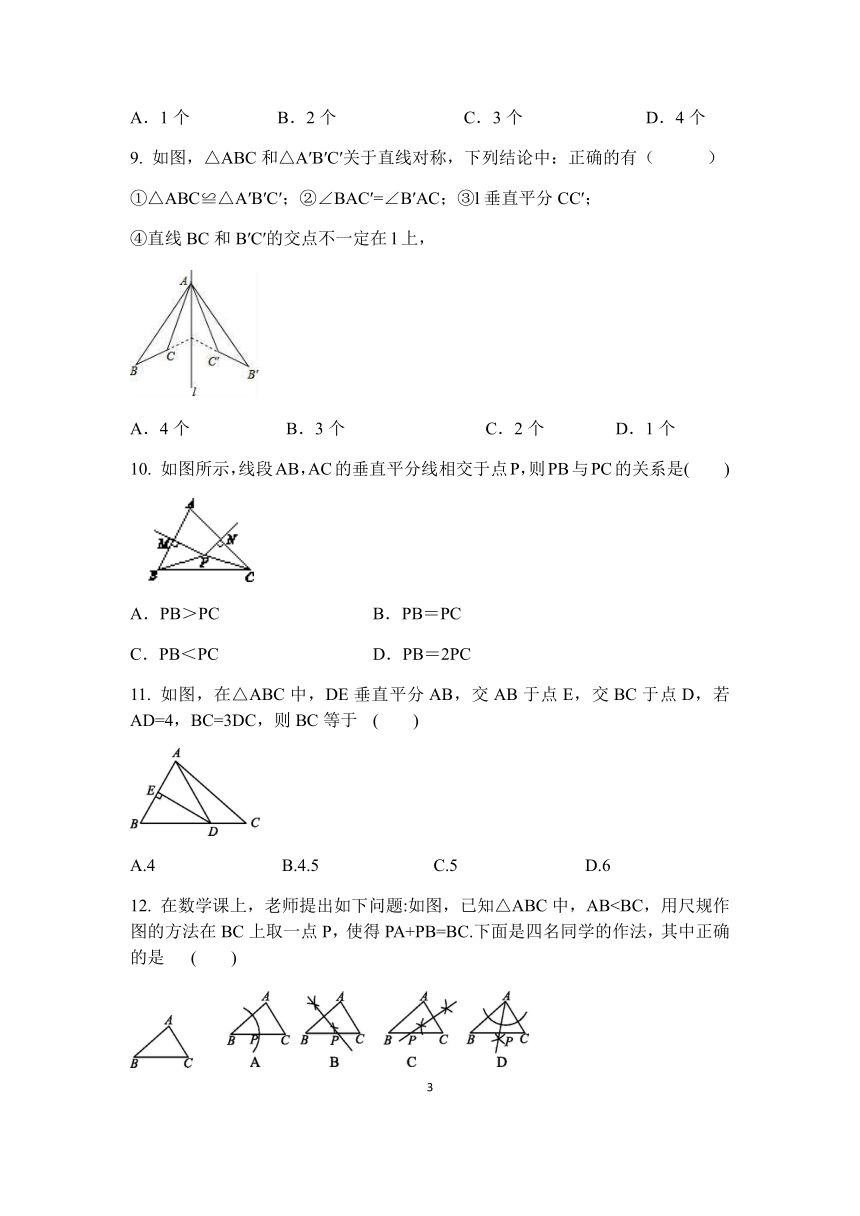
9.
如图,△ABC和△A′B′C′关于直线对称,下列结论中:正确的有(
)
①△ABC≌△A′B′C′;②∠BAC′=∠B′AC;③l垂直平分CC′;
④直线BC和B′C′的交点不一定在l上,
A.4个
B.3个
C.2个
D.1个
10.
如图所示,线段AB,AC的垂直平分线相交于点P,则PB与PC的关系是( )
A.PB>PC
B.PB=PC
C.PB<PC
D.PB=2PC
11.
如图,在△ABC中,DE垂直平分AB,交AB于点E,交BC于点D,若AD=4,BC=3DC,则BC等于
( )
A.4
B.4.5
C.5
D.6
12.
在数学课上,老师提出如下问题:如图,已知△ABC中,AB( )
二、填空题
13.
如图是某时刻在镜子中看到准确时钟的情况,则实际时间是???????
?
14.
若点A(1﹣m,6)与B(2+n,6)关于某坐标轴对称,则m﹣n=
.
15.
如图所示的五角星是轴对称图形,它的对称轴共有________条.
16.
如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有
个.
17.
如图4×5的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有______种.
18.
如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为________.
三、解答题
19.
如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线MN对称的△A′B′C′;
(2)在(1)的结果下,连接AA′,CC′,则六边形AA′B′C′CB的面积为
.
20.
如图所示,两个四边形关于直线l对称,∠C=90°,试写出边a,b的长,并求出∠G的度数.
21.
如图,在四边形ABCD中,AB=AD,BC边的垂直平分线MN经过点A.求证:点A在线段CD的垂直平分线上.
22.
如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若△ABC与△EBC的周长分别是26
cm和16
cm,求AC的长.
23.
如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
24.
如图,已知△ABC.
(1)用直尺和圆规分别作出AB,AC边的垂直平分线l1,l2;
(2)若直线l1,l2的交点为O,连接OB,OC.求证:OB=OC.
人教版数学八年级上册
第十三章
13.1
轴对称
培优练习—参考答案
一、选择题
1.
如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是(
)
A.AB=AD
B.AC平分∠BCD
C.AB=BD
D.△BEC≌△DEC
【答案】C
2.
如图,在△ABC中,BC=8,△ABC的周长为20,BC边的垂直平分线交AB
于点E.则△AEC的周长为( )
A.24
B.20
C.16
D.12
【答案】D
【解答】解:∵△ABC的周长为20,∴AB+AC+BC=20,
∵BC=8,∴AB+AC=12,
∵BC边的垂直平分线交AB于点E,∴EB=EC,
∴△AEC的周长=AE+EC+AC=AE+EB+AC=AB+AC=12,
故选:D.
3.
如下图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
A.①???
?
B.②???
?
C.⑤???
?
D.⑥
【答案】答案为:B
4.
在汉字“生活中的日常用品”中,是轴对称图形的有( )
A.2个
B.3个
C.4个
D.5个
【答案】B
[解析]
根据轴对称图形的定义,在汉字“生活中的日常用品”中,是轴对称图形的有“中”“日”“品”3个.故选B.
5.
如图,在Rt△ABC中∠C=90°,AB>BC,分别以顶点A、B为圆心,大于AB长为半径作圆弧,两条圆弧交于点M、N,作直线MN交边CB于D.若AD=5,CD=3,则BC长是(
)
A.7
B.8
C.12
D.13
【答案】B
6.
将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图4,将图4的纸片展开铺平,再得到的图案是(
)
【答案】答案为:B.
7.
点M(3,2)关于x轴对称的点的坐标为( )
A.
(-3,2)
B.
(3,-2)
C.
(-3,-2)
D.
(3,2)
【答案】B
8.
在4×4的正方形网格中,已将图中的四个小正方形涂上阴影(如图),若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有(
)
A.1个
B.2个
C.3个
D.4个
【答案】C
9.
如图,△ABC和△A′B′C′关于直线对称,下列结论中:正确的有(
)
①△ABC≌△A′B′C′;②∠BAC′=∠B′AC;③l垂直平分CC′;
④直线BC和B′C′的交点不一定在l上,
A.4个
B.3个
C.2个
D.1个
【答案】B
10.
如图所示,线段AB,AC的垂直平分线相交于点P,则PB与PC的关系是( )
A.PB>PC
B.PB=PC
C.PB<PC
D.PB=2PC
【答案】B
[解析]
如图,连接AP.
∵线段AB,AC的垂直平分线相交于点P,∴AP=PB,AP=PC.∴PB=PC.
11.
如图,在△ABC中,DE垂直平分AB,交AB于点E,交BC于点D,若AD=4,BC=3DC,则BC等于
( )
A.4
B.4.5
C.5
D.6
【答案】D
[解析]
∵DE垂直平分AB,AD=4,∴BD=AD=4.
∵BC=3DC,∴BD=2CD.∴CD=2.
∴BC=BD+CD=6.故选D.
12.
在数学课上,老师提出如下问题:如图,已知△ABC中,AB( )
【答案】C
[解析]
∵PA+PB=BC,而PC+PB=BC,∴PA=PC.
∴点P为线段AC的垂直平分线与BC的交点.显然只有选项C符合题意.
二、填空题
13.
如图是某时刻在镜子中看到准确时钟的情况,则实际时间是???????
?
【答案】答案为:4:40.??
14.
若点A(1﹣m,6)与B(2+n,6)关于某坐标轴对称,则m﹣n=
.
【答案】答案为:3.
15.
如图所示的五角星是轴对称图形,它的对称轴共有________条.
【答案】5 [解析]
如图,五角星的对称轴共有5条.
16.
如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有
个.
【答案】答案为:4.
17.
如图4×5的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有______种.
【答案】答案为:4.
18.
如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为________.
【答案】13 【解析】∵DE垂直平分AB,∴AE=BE,
∵AE+EC=8,
∴EC+BE=8,∴△BCE的周长为BE+EC+BC=13.
三、解答题
19.
如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线MN对称的△A′B′C′;
(2)在(1)的结果下,连接AA′,CC′,则六边形AA′B′C′CB的面积为
.
【答案】解:(1)如图所示;
(2)S六边形AA′B′C′CB=3×6﹣×2×1﹣×2×1﹣×2×1﹣×2×1
=18﹣1﹣1﹣1﹣1=14.故答案为:14.
20.
如图所示,两个四边形关于直线l对称,∠C=90°,试写出边a,b的长,并求出∠G的度数.
【答案】
解:∵两个四边形关于直线l对称,
∴四边形ABCD≌四边形FEHG,
∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,a=5
cm,b=4
cm.
∴∠G=360°-∠H-∠E-∠F=55°.
21.
如图,在四边形ABCD中,AB=AD,BC边的垂直平分线MN经过点A.求证:点A在线段CD的垂直平分线上.
【答案】
证明:连接AC.
∵点A在线段BC的垂直平分线MN上,
∴AB=AC.
∵AB=AD,∴AC=AD.
∴点
A在线段CD的垂直平分线上.
22.
如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若△ABC与△EBC的周长分别是26
cm和16
cm,求AC的长.
【答案】
解:∵DE是AB的垂直平分线,∴AE=BE.
∵△EBC的周长是16
cm,
∴BC+BE+EC=16
cm,
即BC+AE+EC=AC+BC=16
cm.
∵△ABC的周长是26
cm,
∴AB+AC+BC=26
cm,
∴AC=AB=10
cm.
23.
如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
【答案】
解:(1)证明:在长方形ABCD中,DA=BC,∠A=∠D=∠B=∠BCD=90°.由折叠的性质,得GC=DA,∠G=∠D=90°,∠GCE=∠A=90°.
∴GC=BC,∠GCF+∠FCE=90°,∠FCE+∠BCE=90°.
∴∠GCF=∠BCE.
又∵∠G=∠B=90°,GC=BC,
∴△FGC≌△EBC(ASA).
(2)由(1)知,DF=GF=BE,
∴S四边形ECGF=S△FGC+S△EFC=S△EBC+S△EFC=S四边形BCFE====16.
24.
如图,已知△ABC.
(1)用直尺和圆规分别作出AB,AC边的垂直平分线l1,l2;
(2)若直线l1,l2的交点为O,连接OB,OC.求证:OB=OC.
【答案】
解:(1)如图所示.
(2)证明:如图,连接OA.
∵l1是AB的垂直平分线,∴OA=OB.
同理,OA=OC.∴OB=OC.
解:(1)如图所示.
(2)证明:如图,连接OA.
∵l1是AB的垂直平分线,∴OA=OB.
同理,OA=OC.∴OB=OC.
2
第十三章
13.1
轴对称
培优练习
一、选择题
1.
如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是(
)
A.AB=AD
B.AC平分∠BCD
C.AB=BD
D.△BEC≌△DEC
2.
如图,在△ABC中,BC=8,△ABC的周长为20,BC边的垂直平分线交AB
于点E.则△AEC的周长为( )
A.24
B.20
C.16
D.12
3.
如下图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
A.①???
?
B.②???
?
C.⑤???
?
D.⑥
4.
在汉字“生活中的日常用品”中,是轴对称图形的有( )
A.2个
B.3个
C.4个
D.5个
5.
如图,在Rt△ABC中∠C=90°,AB>BC,分别以顶点A、B为圆心,大于AB长为半径作圆弧,两条圆弧交于点M、N,作直线MN交边CB于D.若AD=5,CD=3,则BC长是(
)
A.7
B.8
C.12
D.13
6.
将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图4,将图4的纸片展开铺平,再得到的图案是(
)
7.
点M(3,2)关于x轴对称的点的坐标为( )
A.
(-3,2)
B.
(3,-2)
C.
(-3,-2)
D.
(3,2)
8.
在4×4的正方形网格中,已将图中的四个小正方形涂上阴影(如图),若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有(
)
A.1个
B.2个
C.3个
D.4个
9.
如图,△ABC和△A′B′C′关于直线对称,下列结论中:正确的有(
)
①△ABC≌△A′B′C′;②∠BAC′=∠B′AC;③l垂直平分CC′;
④直线BC和B′C′的交点不一定在l上,
A.4个
B.3个
C.2个
D.1个
10.
如图所示,线段AB,AC的垂直平分线相交于点P,则PB与PC的关系是( )
A.PB>PC
B.PB=PC
C.PB<PC
D.PB=2PC
11.
如图,在△ABC中,DE垂直平分AB,交AB于点E,交BC于点D,若AD=4,BC=3DC,则BC等于
( )
A.4
B.4.5
C.5
D.6
12.
在数学课上,老师提出如下问题:如图,已知△ABC中,AB
二、填空题
13.
如图是某时刻在镜子中看到准确时钟的情况,则实际时间是???????
?
14.
若点A(1﹣m,6)与B(2+n,6)关于某坐标轴对称,则m﹣n=
.
15.
如图所示的五角星是轴对称图形,它的对称轴共有________条.
16.
如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有
个.
17.
如图4×5的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有______种.
18.
如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为________.
三、解答题
19.
如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线MN对称的△A′B′C′;
(2)在(1)的结果下,连接AA′,CC′,则六边形AA′B′C′CB的面积为
.
20.
如图所示,两个四边形关于直线l对称,∠C=90°,试写出边a,b的长,并求出∠G的度数.
21.
如图,在四边形ABCD中,AB=AD,BC边的垂直平分线MN经过点A.求证:点A在线段CD的垂直平分线上.
22.
如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若△ABC与△EBC的周长分别是26
cm和16
cm,求AC的长.
23.
如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
24.
如图,已知△ABC.
(1)用直尺和圆规分别作出AB,AC边的垂直平分线l1,l2;
(2)若直线l1,l2的交点为O,连接OB,OC.求证:OB=OC.
人教版数学八年级上册
第十三章
13.1
轴对称
培优练习—参考答案
一、选择题
1.
如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是(
)
A.AB=AD
B.AC平分∠BCD
C.AB=BD
D.△BEC≌△DEC
【答案】C
2.
如图,在△ABC中,BC=8,△ABC的周长为20,BC边的垂直平分线交AB
于点E.则△AEC的周长为( )
A.24
B.20
C.16
D.12
【答案】D
【解答】解:∵△ABC的周长为20,∴AB+AC+BC=20,
∵BC=8,∴AB+AC=12,
∵BC边的垂直平分线交AB于点E,∴EB=EC,
∴△AEC的周长=AE+EC+AC=AE+EB+AC=AB+AC=12,
故选:D.
3.
如下图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
A.①???
?
B.②???
?
C.⑤???
?
D.⑥
【答案】答案为:B
4.
在汉字“生活中的日常用品”中,是轴对称图形的有( )
A.2个
B.3个
C.4个
D.5个
【答案】B
[解析]
根据轴对称图形的定义,在汉字“生活中的日常用品”中,是轴对称图形的有“中”“日”“品”3个.故选B.
5.
如图,在Rt△ABC中∠C=90°,AB>BC,分别以顶点A、B为圆心,大于AB长为半径作圆弧,两条圆弧交于点M、N,作直线MN交边CB于D.若AD=5,CD=3,则BC长是(
)
A.7
B.8
C.12
D.13
【答案】B
6.
将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图4,将图4的纸片展开铺平,再得到的图案是(
)
【答案】答案为:B.
7.
点M(3,2)关于x轴对称的点的坐标为( )
A.
(-3,2)
B.
(3,-2)
C.
(-3,-2)
D.
(3,2)
【答案】B
8.
在4×4的正方形网格中,已将图中的四个小正方形涂上阴影(如图),若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有(
)
A.1个
B.2个
C.3个
D.4个
【答案】C
9.
如图,△ABC和△A′B′C′关于直线对称,下列结论中:正确的有(
)
①△ABC≌△A′B′C′;②∠BAC′=∠B′AC;③l垂直平分CC′;
④直线BC和B′C′的交点不一定在l上,
A.4个
B.3个
C.2个
D.1个
【答案】B
10.
如图所示,线段AB,AC的垂直平分线相交于点P,则PB与PC的关系是( )
A.PB>PC
B.PB=PC
C.PB<PC
D.PB=2PC
【答案】B
[解析]
如图,连接AP.
∵线段AB,AC的垂直平分线相交于点P,∴AP=PB,AP=PC.∴PB=PC.
11.
如图,在△ABC中,DE垂直平分AB,交AB于点E,交BC于点D,若AD=4,BC=3DC,则BC等于
( )
A.4
B.4.5
C.5
D.6
【答案】D
[解析]
∵DE垂直平分AB,AD=4,∴BD=AD=4.
∵BC=3DC,∴BD=2CD.∴CD=2.
∴BC=BD+CD=6.故选D.
12.
在数学课上,老师提出如下问题:如图,已知△ABC中,AB
【答案】C
[解析]
∵PA+PB=BC,而PC+PB=BC,∴PA=PC.
∴点P为线段AC的垂直平分线与BC的交点.显然只有选项C符合题意.
二、填空题
13.
如图是某时刻在镜子中看到准确时钟的情况,则实际时间是???????
?
【答案】答案为:4:40.??
14.
若点A(1﹣m,6)与B(2+n,6)关于某坐标轴对称,则m﹣n=
.
【答案】答案为:3.
15.
如图所示的五角星是轴对称图形,它的对称轴共有________条.
【答案】5 [解析]
如图,五角星的对称轴共有5条.
16.
如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有
个.
【答案】答案为:4.
17.
如图4×5的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有______种.
【答案】答案为:4.
18.
如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为________.
【答案】13 【解析】∵DE垂直平分AB,∴AE=BE,
∵AE+EC=8,
∴EC+BE=8,∴△BCE的周长为BE+EC+BC=13.
三、解答题
19.
如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线MN对称的△A′B′C′;
(2)在(1)的结果下,连接AA′,CC′,则六边形AA′B′C′CB的面积为
.
【答案】解:(1)如图所示;
(2)S六边形AA′B′C′CB=3×6﹣×2×1﹣×2×1﹣×2×1﹣×2×1
=18﹣1﹣1﹣1﹣1=14.故答案为:14.
20.
如图所示,两个四边形关于直线l对称,∠C=90°,试写出边a,b的长,并求出∠G的度数.
【答案】
解:∵两个四边形关于直线l对称,
∴四边形ABCD≌四边形FEHG,
∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,a=5
cm,b=4
cm.
∴∠G=360°-∠H-∠E-∠F=55°.
21.
如图,在四边形ABCD中,AB=AD,BC边的垂直平分线MN经过点A.求证:点A在线段CD的垂直平分线上.
【答案】
证明:连接AC.
∵点A在线段BC的垂直平分线MN上,
∴AB=AC.
∵AB=AD,∴AC=AD.
∴点
A在线段CD的垂直平分线上.
22.
如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若△ABC与△EBC的周长分别是26
cm和16
cm,求AC的长.
【答案】
解:∵DE是AB的垂直平分线,∴AE=BE.
∵△EBC的周长是16
cm,
∴BC+BE+EC=16
cm,
即BC+AE+EC=AC+BC=16
cm.
∵△ABC的周长是26
cm,
∴AB+AC+BC=26
cm,
∴AC=AB=10
cm.
23.
如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
【答案】
解:(1)证明:在长方形ABCD中,DA=BC,∠A=∠D=∠B=∠BCD=90°.由折叠的性质,得GC=DA,∠G=∠D=90°,∠GCE=∠A=90°.
∴GC=BC,∠GCF+∠FCE=90°,∠FCE+∠BCE=90°.
∴∠GCF=∠BCE.
又∵∠G=∠B=90°,GC=BC,
∴△FGC≌△EBC(ASA).
(2)由(1)知,DF=GF=BE,
∴S四边形ECGF=S△FGC+S△EFC=S△EBC+S△EFC=S四边形BCFE====16.
24.
如图,已知△ABC.
(1)用直尺和圆规分别作出AB,AC边的垂直平分线l1,l2;
(2)若直线l1,l2的交点为O,连接OB,OC.求证:OB=OC.
【答案】
解:(1)如图所示.
(2)证明:如图,连接OA.
∵l1是AB的垂直平分线,∴OA=OB.
同理,OA=OC.∴OB=OC.
解:(1)如图所示.
(2)证明:如图,连接OA.
∵l1是AB的垂直平分线,∴OA=OB.
同理,OA=OC.∴OB=OC.
2
