北师大版八年级上册数学 7.5三角形内角和定理 同步测试(Word版 含解析)
文档属性
| 名称 | 北师大版八年级上册数学 7.5三角形内角和定理 同步测试(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 201.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 11:36:08 | ||
图片预览



文档简介
7.5三角形内角和定理 同步测试
一.选择题
1.下列条件中,能确定三角形是直角三角形的是( )
A.∠A=∠B=∠C B.∠A+∠B=∠C
C.∠A=∠B=30° D.
2.如图,△ABC的两条内角平分线BE、CD相交于点F,∠A=62°,则∠BFC的度数是( )
A.59° B.118° C.121° D.124°
3.如图,AB和CD相交于点O,∠A=∠C,则下列结论中不能完全确定正确的是( )
A.∠B=∠D B.∠1=∠A+∠D C.∠2>∠D D.∠C=∠D
4.如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=108°,则∠DAC的度数为( )
A.80° B.82° C.84° D.86°
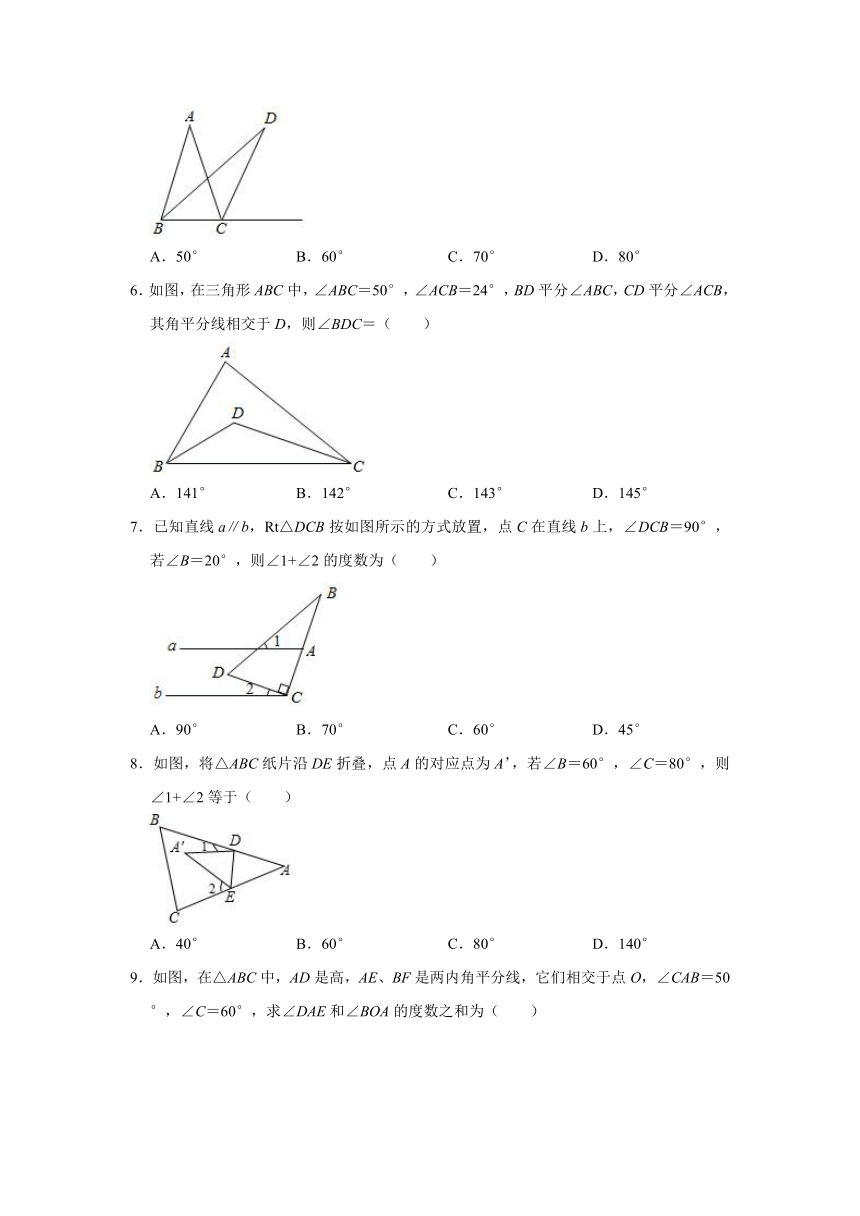
5.如图,在△ABC中,∠ABC的平分线BD与∠ACB的外角平分线CD相交于点D,∠D=30°,则∠A等于( )
A.50° B.60° C.70° D.80°
6.如图,在三角形ABC中,∠ABC=50°,∠ACB=24°,BD平分∠ABC,CD平分∠ACB,其角平分线相交于D,则∠BDC=( )
A.141° B.142° C.143° D.145°
7.已知直线a∥b,Rt△DCB按如图所示的方式放置,点C在直线b上,∠DCB=90°,若∠B=20°,则∠1+∠2的度数为( )
A.90° B.70° C.60° D.45°
8.如图,将△ABC纸片沿DE折叠,点A的对应点为A’,若∠B=60°,∠C=80°,则∠1+∠2等于( )
A.40° B.60° C.80° D.140°
9.如图,在△ABC中,AD是高,AE、BF是两内角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数之和为( )
A.115° B.120° C.125° D.130°
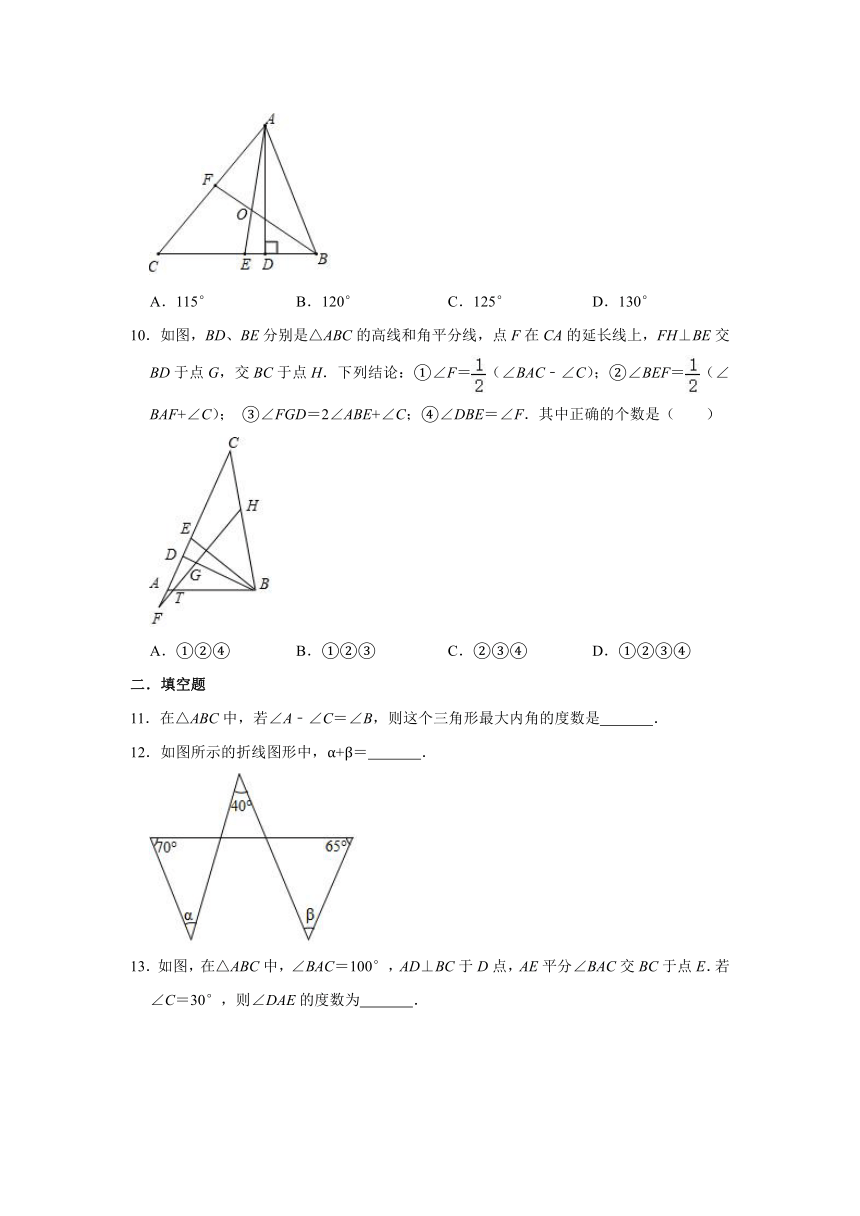
10.如图,BD、BE分别是△ABC的高线和角平分线,点F在CA的延长线上,FH⊥BE交BD于点G,交BC于点H.下列结论:①∠F=(∠BAC﹣∠C);②∠BEF=(∠BAF+∠C); ③∠FGD=2∠ABE+∠C;④∠DBE=∠F.其中正确的个数是( )
A.①②④ B.①②③ C.②③④ D.①②③④
二.填空题
11.在△ABC中,若∠A﹣∠C=∠B,则这个三角形最大内角的度数是 .
12.如图所示的折线图形中,α+β= .
13.如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=30°,则∠DAE的度数为 .
14.已知,AD是△ABC的角平分线,MN⊥AD于点D,分别交AB、射线AC于点M、N,∠MDB=10°,则∠ACB﹣∠ABC= °.
15.如图1,△ABC中,有一块直角三角板PMN放置在△ABC上(P点在△ABC内),使三角板PMN的两条直角边PM、PN恰好分别经过点B和点C.
(1)若∠A=52°,则∠1+∠2= °;
(2)如图2,改变直角三角板PMN的位置;使P点在△ABC外,三角板PMN的两条直角边PM、PN仍然分别经过点B和点C,∠1,∠2与∠A的关系是 .
三.解答题
16.如图,在△ABC中,AD⊥BC,垂足是D,∠B=70°,∠BAC=46°.求∠CAD的度数.
17.如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P,∠BDC=58°,求∠BAP的度数.
18.小亮在学习中遇到这样一个问题:
如图1,在△ABC中,∠C>∠B,AE平分∠BAC,AD⊥BC于D.
猜想∠B、∠C、∠EAD的数量关系,说明理由.
(1)小亮阅读题目后,没有发现数量关系与解题思路.于是尝试带入∠B、∠C的值求∠EAD值,得到下面几组对应值:
∠B/度 10 30 30 20 20
∠C/度 70 70 60 60 80
∠EAD/度 30 20 15 a 30
上表中a= .
(2)猜想∠B、∠C、∠EAD的数量关系,说明理由.
(3)小亮突发奇想,交换B、C两个字母位置,如图2,过EA的延长线是一点F作FD⊥BC交CB的延长线于D,当∠B=80°、∠C=20°时,∠F度数为 °.
参考答案
一.选择题
1.解:A、由∠A=∠B=∠C,可知△ABC是等边三角形,本选项不符合题意.
B、由∠A+∠B=∠C,推出∠C=90°,本选项符合题意.
C、由∠A=∠B=30°,推出∠C=120°,△ABC是钝角三角形,本选项不符合题意.
D、由∠A=∠B=∠C,推出∠C=()°>90°,本选项不符合题意.
故选:B.
2.解:在△ABC中,∠ABC+∠ACB=180°﹣∠A=180°﹣62°=118°,
∵∠ABC,∠ACB的平分线BE,CD相交于点F,
∴∠FBC=∠ABC,∠FCB=∠ACB,
∴∠FBC+∠FCB=(∠ABC+∠ACB)=×118°=59°,
在△BCF中,∠BFC=180°﹣(∠FBC+∠FCB)=180°﹣59°=121°.
故选:C.
3.解:∵∠A+∠AOD+∠D=180°,∠C+∠COB+∠B=180°,∠A=∠C,∠AOD=∠BOC,
∴∠B=∠D,
∵∠1=∠2=∠A+∠D,
∴∠2>∠D,
故选项A,B,C正确,
故选:D.
4.解:设∠1=∠2=x,
∵∠4=∠3=∠1+∠2=2x,
∴∠DAC=180°﹣4x,
∵∠BAC=108°,
∴x+180°﹣4x=108°,
∴x=24°,
∴∠DAC=180°﹣4×24°=84°.
故选:C.
5.解:设点E在BC的延长线上,AC与BD交于点F,如图所示.
∵∠DCE=∠DBC+∠D,CD平分∠ACE,
∴∠ACD=∠DCE=∠DBC+∠D.
∵BD平分∠ABC,
∴∠ABF=∠DBC.
又∵∠ABF+∠A+∠AFB=180°,∠DCF+∠D+∠CFD=180°,∠AFB=∠CFD,
∴∠ABF+∠A=∠DCF+∠D,即∠ABF+∠A=∠DBC+∠D+∠D,
∴∠A=2∠D=2×30°=60°.
故选:B.
6.解:∵BD平分∠ABC,
∴∠DBC=∠ABC=×50°=25°,
∵CD平分∠ACB,
∴∠DCB=∠ACB=×24°=12°,
∴∠BDC=180°﹣∠DBC﹣∠DCB
=180°﹣25°﹣12°
=143°.
故选:C.
7.解:如图,延长BD交直线b于点M.
∵∠DCB=90°,∠B=20°,
∴∠BDC=90°﹣20°=70°,
∵a∥b,
∴∠1=∠BMC,
∵∠BDC=∠DMC+∠2=∠1+∠2,
∴∠1+∠2=70°,
故选:B.
8.解:连接AA′.
∵∠B=60°,∠C=80°,
∴∠A=40°
∵∠1=∠EA′A+∠EAA′,∠2=∠DA′A+∠DAA′,∠BCA=∠EA′D,
∴∠1+∠2=∠EA′A+∠EAA′+∠DA′A+∠DAA′=∠EAD+∠EA′D=2∠EAD=80°,
故选:C.
9.解:∵∠CAB=50°,∠C=60°
∴∠ABC=180°﹣50°﹣60°=70°,
又∵AD是高,
∴∠ADC=90°,
∴∠DAC=180°﹣90°﹣∠C=30°,
∵AE、BF是角平分线,
∴∠CBF=∠ABF=35°,∠EAF=25°,
∴∠DAE=∠DAC﹣∠EAF=5°,
∠AFB=∠C+∠CBF=60°+35°=95°,
∴∠BOA=∠EAF+∠AFB=25°+95°=120°,
∴∠DAE+∠BOA=5°+120°=125°.
故选:C.
10.解:∵BD⊥FD,
∴∠FGD+∠F=90°,
∵FH⊥BE,
∴∠BGH+∠DBE=90°,
∵∠FGD=∠BGH,
∴∠DBE=∠F,故④正确;
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∠BEF=∠CBE+∠C,
∴2∠BEF=∠ABC+2∠C,
∠BAF=∠ABC+∠C,
∴2∠BEF=∠BAF+∠C,即∠BEF=(∠BAF+∠C),故②正确;
∵∠AEB=∠EBC+∠C,
∵∠ABE=∠CBE,
∴∠AEB=∠ABE+∠C,
∵BD⊥FC,FH⊥BE,
∴∠FGD=∠FEB,
∴∠FGD=∠CBE+∠C=∠ABE+∠C,故③错误,
∵∠ABD=90°﹣∠BAC,∠DBE=∠ABE﹣∠ABD=∠ABE﹣90°+∠BAC=∠CBD﹣∠DBE﹣90°+∠BAC,∠CBD=90°﹣∠C,
∴∠DBE=∠BAC﹣∠C﹣∠DBE,
∵∠DBE=∠F,
∴∠F=∠BAC﹣∠C﹣∠DBE,
∴∠F=(∠BAC﹣∠C);故①正确;
故选:A.
二.填空题
11.解:∵∠A﹣∠C=∠B,
∴∠A=∠C+∠B,
∵∠A+∠B+∠C=180°,
∴∠A=90°,
即这个三角形最大内角的度数是90°,
故答案为:90°.
12.解:如图,连接BC.
在△EBC中,∠1+∠2=180°﹣∠E=140°,
在四边形ABCD中,∠A+∠ABC+∠BCD+∠D=360°,
∴70°+α+∠1+∠2+β+65°=360°,
∴α+β=360°﹣70°﹣65°﹣140°=85°,
故答案为85°.
13.解:∵AE平分∠BAC,
∴∠EAC=∠BAC=×100°=50°,
∵∠C=30°,
∴∠AED=∠C+∠EAC=30°+50°=80°,
∵AD⊥BC,
∴∠ADE=90°,
∴∠DAE=90°﹣80°=10°,
故答案为:10°.
14.解:∵AD是△ABC的角平分线,MN⊥AD于点D,
∴AM=AN.
∴∠AMN=∠AND.
∵∠MDB=∠CDN=10°,
∵∠ACB=∠AND+∠CDN,
∠ABC=∠AMN﹣∠MDB,
∴∠ACB﹣∠ABC
=∠AND+∠CDN﹣∠AMN+∠MDB
=∠CDN+∠MDB
=20°.
故答案为:20.
15.解:(1)∵∠A=52°,
∴∠ABC+∠ACB=180°﹣52°=128°,
∵∠P=90°,
∴∠PBC+∠PCB=90°,
∴∠ABP+∠ACP=128°﹣90°=38°,
即∠1+∠2=38°.
故答案为:38;
(2)∠2﹣∠1=90°﹣∠A.理由如下:
在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵∠MPN=90°,
∴∠PBC+∠PCB=90°,
∴(∠ABC+∠ACB)﹣(∠PBC+∠PCB)=180°﹣∠A﹣90°,
即∠ABC+∠ACP+∠PCB﹣∠ABP﹣∠ABC﹣∠PCB=90°﹣∠A,
∴∠ACP﹣∠ABP=90°﹣∠A.
即∠2﹣∠1=90°﹣∠A;
故答案为:∠2﹣∠1=90°﹣∠A.
三.解答题
16.解:∵AD⊥BC,
∴∠BDA=90°,
∴∠BAD=90°﹣∠B=20°,
∴∠CAD=∠BAC﹣∠BAD
=46°﹣20°=26°.
17.解:∵∠BDC=58°,∠C=90°,
∴∠DBC=90°﹣∠BDC=32°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=32°,
∴∠ABC=2∠ABD=64°,
∴∠CAB=90°﹣∠ABC=26°,
∵PA平分∠BAC,
∴∠BAP=∠CAB=13°.
18.解:(1)a=20,
故答案为20.
(2)猜想:∠EAD=(∠C﹣∠B).
理由:∵AD⊥BC,
∴∠DAC=90°﹣∠C,
∵AE平分∠BAC,∠BAC=180°﹣∠B﹣∠C,
∴∠EAC=∠BAC=90°﹣∠B﹣∠C,
∴∠EAD=∠EAC﹣∠DAC=90°﹣∠B﹣∠C﹣(90°﹣∠C)=(∠C﹣∠B).
(3)如图2中,过点A作AH⊥CD于H.
∵AH⊥CD,FD⊥CD,
∴AH∥DF,
∴∠F=∠EAH=(∠B﹣∠C)=(80°﹣20°)=30°.
故答案为30.
一.选择题
1.下列条件中,能确定三角形是直角三角形的是( )
A.∠A=∠B=∠C B.∠A+∠B=∠C
C.∠A=∠B=30° D.
2.如图,△ABC的两条内角平分线BE、CD相交于点F,∠A=62°,则∠BFC的度数是( )
A.59° B.118° C.121° D.124°
3.如图,AB和CD相交于点O,∠A=∠C,则下列结论中不能完全确定正确的是( )
A.∠B=∠D B.∠1=∠A+∠D C.∠2>∠D D.∠C=∠D
4.如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=108°,则∠DAC的度数为( )
A.80° B.82° C.84° D.86°
5.如图,在△ABC中,∠ABC的平分线BD与∠ACB的外角平分线CD相交于点D,∠D=30°,则∠A等于( )
A.50° B.60° C.70° D.80°
6.如图,在三角形ABC中,∠ABC=50°,∠ACB=24°,BD平分∠ABC,CD平分∠ACB,其角平分线相交于D,则∠BDC=( )
A.141° B.142° C.143° D.145°
7.已知直线a∥b,Rt△DCB按如图所示的方式放置,点C在直线b上,∠DCB=90°,若∠B=20°,则∠1+∠2的度数为( )
A.90° B.70° C.60° D.45°
8.如图,将△ABC纸片沿DE折叠,点A的对应点为A’,若∠B=60°,∠C=80°,则∠1+∠2等于( )
A.40° B.60° C.80° D.140°
9.如图,在△ABC中,AD是高,AE、BF是两内角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数之和为( )
A.115° B.120° C.125° D.130°
10.如图,BD、BE分别是△ABC的高线和角平分线,点F在CA的延长线上,FH⊥BE交BD于点G,交BC于点H.下列结论:①∠F=(∠BAC﹣∠C);②∠BEF=(∠BAF+∠C); ③∠FGD=2∠ABE+∠C;④∠DBE=∠F.其中正确的个数是( )
A.①②④ B.①②③ C.②③④ D.①②③④
二.填空题
11.在△ABC中,若∠A﹣∠C=∠B,则这个三角形最大内角的度数是 .
12.如图所示的折线图形中,α+β= .
13.如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=30°,则∠DAE的度数为 .
14.已知,AD是△ABC的角平分线,MN⊥AD于点D,分别交AB、射线AC于点M、N,∠MDB=10°,则∠ACB﹣∠ABC= °.
15.如图1,△ABC中,有一块直角三角板PMN放置在△ABC上(P点在△ABC内),使三角板PMN的两条直角边PM、PN恰好分别经过点B和点C.
(1)若∠A=52°,则∠1+∠2= °;
(2)如图2,改变直角三角板PMN的位置;使P点在△ABC外,三角板PMN的两条直角边PM、PN仍然分别经过点B和点C,∠1,∠2与∠A的关系是 .
三.解答题
16.如图,在△ABC中,AD⊥BC,垂足是D,∠B=70°,∠BAC=46°.求∠CAD的度数.
17.如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P,∠BDC=58°,求∠BAP的度数.
18.小亮在学习中遇到这样一个问题:
如图1,在△ABC中,∠C>∠B,AE平分∠BAC,AD⊥BC于D.
猜想∠B、∠C、∠EAD的数量关系,说明理由.
(1)小亮阅读题目后,没有发现数量关系与解题思路.于是尝试带入∠B、∠C的值求∠EAD值,得到下面几组对应值:
∠B/度 10 30 30 20 20
∠C/度 70 70 60 60 80
∠EAD/度 30 20 15 a 30
上表中a= .
(2)猜想∠B、∠C、∠EAD的数量关系,说明理由.
(3)小亮突发奇想,交换B、C两个字母位置,如图2,过EA的延长线是一点F作FD⊥BC交CB的延长线于D,当∠B=80°、∠C=20°时,∠F度数为 °.
参考答案
一.选择题
1.解:A、由∠A=∠B=∠C,可知△ABC是等边三角形,本选项不符合题意.
B、由∠A+∠B=∠C,推出∠C=90°,本选项符合题意.
C、由∠A=∠B=30°,推出∠C=120°,△ABC是钝角三角形,本选项不符合题意.
D、由∠A=∠B=∠C,推出∠C=()°>90°,本选项不符合题意.
故选:B.
2.解:在△ABC中,∠ABC+∠ACB=180°﹣∠A=180°﹣62°=118°,
∵∠ABC,∠ACB的平分线BE,CD相交于点F,
∴∠FBC=∠ABC,∠FCB=∠ACB,
∴∠FBC+∠FCB=(∠ABC+∠ACB)=×118°=59°,
在△BCF中,∠BFC=180°﹣(∠FBC+∠FCB)=180°﹣59°=121°.
故选:C.
3.解:∵∠A+∠AOD+∠D=180°,∠C+∠COB+∠B=180°,∠A=∠C,∠AOD=∠BOC,
∴∠B=∠D,
∵∠1=∠2=∠A+∠D,
∴∠2>∠D,
故选项A,B,C正确,
故选:D.
4.解:设∠1=∠2=x,
∵∠4=∠3=∠1+∠2=2x,
∴∠DAC=180°﹣4x,
∵∠BAC=108°,
∴x+180°﹣4x=108°,
∴x=24°,
∴∠DAC=180°﹣4×24°=84°.
故选:C.
5.解:设点E在BC的延长线上,AC与BD交于点F,如图所示.
∵∠DCE=∠DBC+∠D,CD平分∠ACE,
∴∠ACD=∠DCE=∠DBC+∠D.
∵BD平分∠ABC,
∴∠ABF=∠DBC.
又∵∠ABF+∠A+∠AFB=180°,∠DCF+∠D+∠CFD=180°,∠AFB=∠CFD,
∴∠ABF+∠A=∠DCF+∠D,即∠ABF+∠A=∠DBC+∠D+∠D,
∴∠A=2∠D=2×30°=60°.
故选:B.
6.解:∵BD平分∠ABC,
∴∠DBC=∠ABC=×50°=25°,
∵CD平分∠ACB,
∴∠DCB=∠ACB=×24°=12°,
∴∠BDC=180°﹣∠DBC﹣∠DCB
=180°﹣25°﹣12°
=143°.
故选:C.
7.解:如图,延长BD交直线b于点M.
∵∠DCB=90°,∠B=20°,
∴∠BDC=90°﹣20°=70°,
∵a∥b,
∴∠1=∠BMC,
∵∠BDC=∠DMC+∠2=∠1+∠2,
∴∠1+∠2=70°,
故选:B.
8.解:连接AA′.
∵∠B=60°,∠C=80°,
∴∠A=40°
∵∠1=∠EA′A+∠EAA′,∠2=∠DA′A+∠DAA′,∠BCA=∠EA′D,
∴∠1+∠2=∠EA′A+∠EAA′+∠DA′A+∠DAA′=∠EAD+∠EA′D=2∠EAD=80°,
故选:C.
9.解:∵∠CAB=50°,∠C=60°
∴∠ABC=180°﹣50°﹣60°=70°,
又∵AD是高,
∴∠ADC=90°,
∴∠DAC=180°﹣90°﹣∠C=30°,
∵AE、BF是角平分线,
∴∠CBF=∠ABF=35°,∠EAF=25°,
∴∠DAE=∠DAC﹣∠EAF=5°,
∠AFB=∠C+∠CBF=60°+35°=95°,
∴∠BOA=∠EAF+∠AFB=25°+95°=120°,
∴∠DAE+∠BOA=5°+120°=125°.
故选:C.
10.解:∵BD⊥FD,
∴∠FGD+∠F=90°,
∵FH⊥BE,
∴∠BGH+∠DBE=90°,
∵∠FGD=∠BGH,
∴∠DBE=∠F,故④正确;
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∠BEF=∠CBE+∠C,
∴2∠BEF=∠ABC+2∠C,
∠BAF=∠ABC+∠C,
∴2∠BEF=∠BAF+∠C,即∠BEF=(∠BAF+∠C),故②正确;
∵∠AEB=∠EBC+∠C,
∵∠ABE=∠CBE,
∴∠AEB=∠ABE+∠C,
∵BD⊥FC,FH⊥BE,
∴∠FGD=∠FEB,
∴∠FGD=∠CBE+∠C=∠ABE+∠C,故③错误,
∵∠ABD=90°﹣∠BAC,∠DBE=∠ABE﹣∠ABD=∠ABE﹣90°+∠BAC=∠CBD﹣∠DBE﹣90°+∠BAC,∠CBD=90°﹣∠C,
∴∠DBE=∠BAC﹣∠C﹣∠DBE,
∵∠DBE=∠F,
∴∠F=∠BAC﹣∠C﹣∠DBE,
∴∠F=(∠BAC﹣∠C);故①正确;
故选:A.
二.填空题
11.解:∵∠A﹣∠C=∠B,
∴∠A=∠C+∠B,
∵∠A+∠B+∠C=180°,
∴∠A=90°,
即这个三角形最大内角的度数是90°,
故答案为:90°.
12.解:如图,连接BC.
在△EBC中,∠1+∠2=180°﹣∠E=140°,
在四边形ABCD中,∠A+∠ABC+∠BCD+∠D=360°,
∴70°+α+∠1+∠2+β+65°=360°,
∴α+β=360°﹣70°﹣65°﹣140°=85°,
故答案为85°.
13.解:∵AE平分∠BAC,
∴∠EAC=∠BAC=×100°=50°,
∵∠C=30°,
∴∠AED=∠C+∠EAC=30°+50°=80°,
∵AD⊥BC,
∴∠ADE=90°,
∴∠DAE=90°﹣80°=10°,
故答案为:10°.
14.解:∵AD是△ABC的角平分线,MN⊥AD于点D,
∴AM=AN.
∴∠AMN=∠AND.
∵∠MDB=∠CDN=10°,
∵∠ACB=∠AND+∠CDN,
∠ABC=∠AMN﹣∠MDB,
∴∠ACB﹣∠ABC
=∠AND+∠CDN﹣∠AMN+∠MDB
=∠CDN+∠MDB
=20°.
故答案为:20.
15.解:(1)∵∠A=52°,
∴∠ABC+∠ACB=180°﹣52°=128°,
∵∠P=90°,
∴∠PBC+∠PCB=90°,
∴∠ABP+∠ACP=128°﹣90°=38°,
即∠1+∠2=38°.
故答案为:38;
(2)∠2﹣∠1=90°﹣∠A.理由如下:
在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵∠MPN=90°,
∴∠PBC+∠PCB=90°,
∴(∠ABC+∠ACB)﹣(∠PBC+∠PCB)=180°﹣∠A﹣90°,
即∠ABC+∠ACP+∠PCB﹣∠ABP﹣∠ABC﹣∠PCB=90°﹣∠A,
∴∠ACP﹣∠ABP=90°﹣∠A.
即∠2﹣∠1=90°﹣∠A;
故答案为:∠2﹣∠1=90°﹣∠A.
三.解答题
16.解:∵AD⊥BC,
∴∠BDA=90°,
∴∠BAD=90°﹣∠B=20°,
∴∠CAD=∠BAC﹣∠BAD
=46°﹣20°=26°.
17.解:∵∠BDC=58°,∠C=90°,
∴∠DBC=90°﹣∠BDC=32°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=32°,
∴∠ABC=2∠ABD=64°,
∴∠CAB=90°﹣∠ABC=26°,
∵PA平分∠BAC,
∴∠BAP=∠CAB=13°.
18.解:(1)a=20,
故答案为20.
(2)猜想:∠EAD=(∠C﹣∠B).
理由:∵AD⊥BC,
∴∠DAC=90°﹣∠C,
∵AE平分∠BAC,∠BAC=180°﹣∠B﹣∠C,
∴∠EAC=∠BAC=90°﹣∠B﹣∠C,
∴∠EAD=∠EAC﹣∠DAC=90°﹣∠B﹣∠C﹣(90°﹣∠C)=(∠C﹣∠B).
(3)如图2中,过点A作AH⊥CD于H.
∵AH⊥CD,FD⊥CD,
∴AH∥DF,
∴∠F=∠EAH=(∠B﹣∠C)=(80°﹣20°)=30°.
故答案为30.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
