2020-2021苏科版八年级上学期数学第6章一次函数章末培优训练卷(1)(word版含解析)
文档属性
| 名称 | 2020-2021苏科版八年级上学期数学第6章一次函数章末培优训练卷(1)(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 305.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 12:10:45 | ||
图片预览

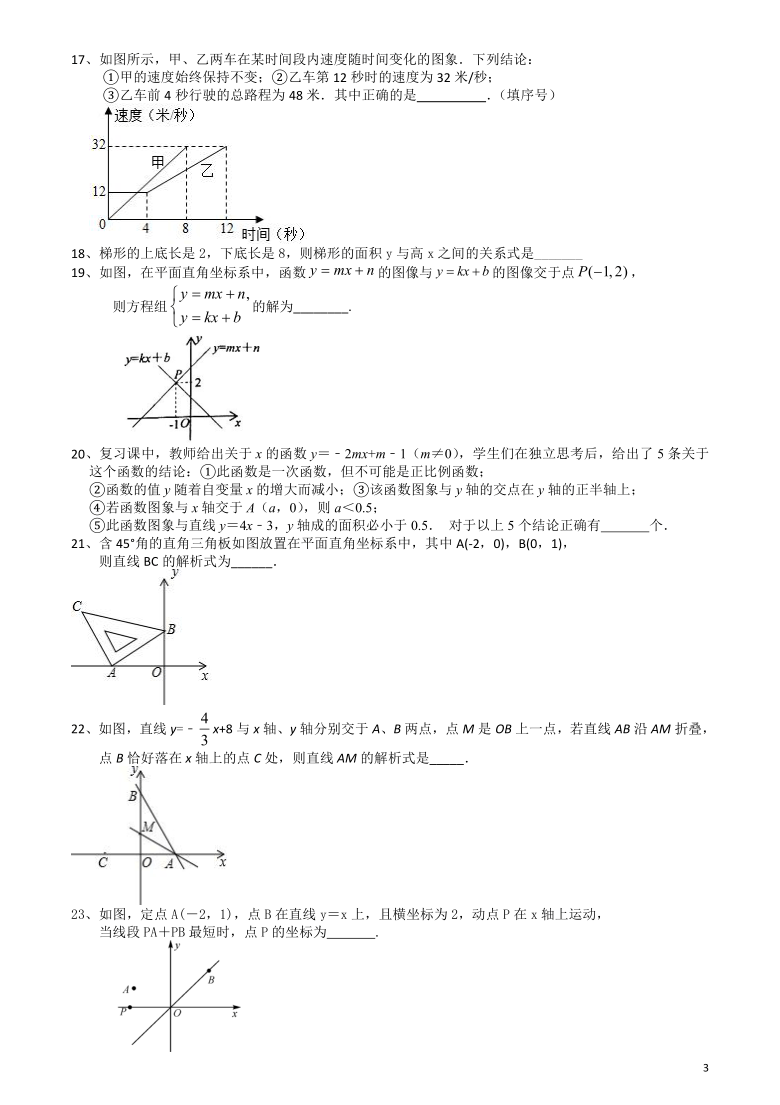

文档简介
2020-2021苏科版八年级上学期数学第6章一次函数
章末培优训练卷(1)
一、选择题
1、函数y=2+中自变量x的取值范围是( )
A.x≥2
B.x
C.x
D.x
2、下列函数:①y=x;②y=2x-1;③y=;④y=x2-1中,是一次函数的有(
)
A.4个
B.3个
C.2个
D.1个
3、若是一次函数,则m的值为(
)
A.2
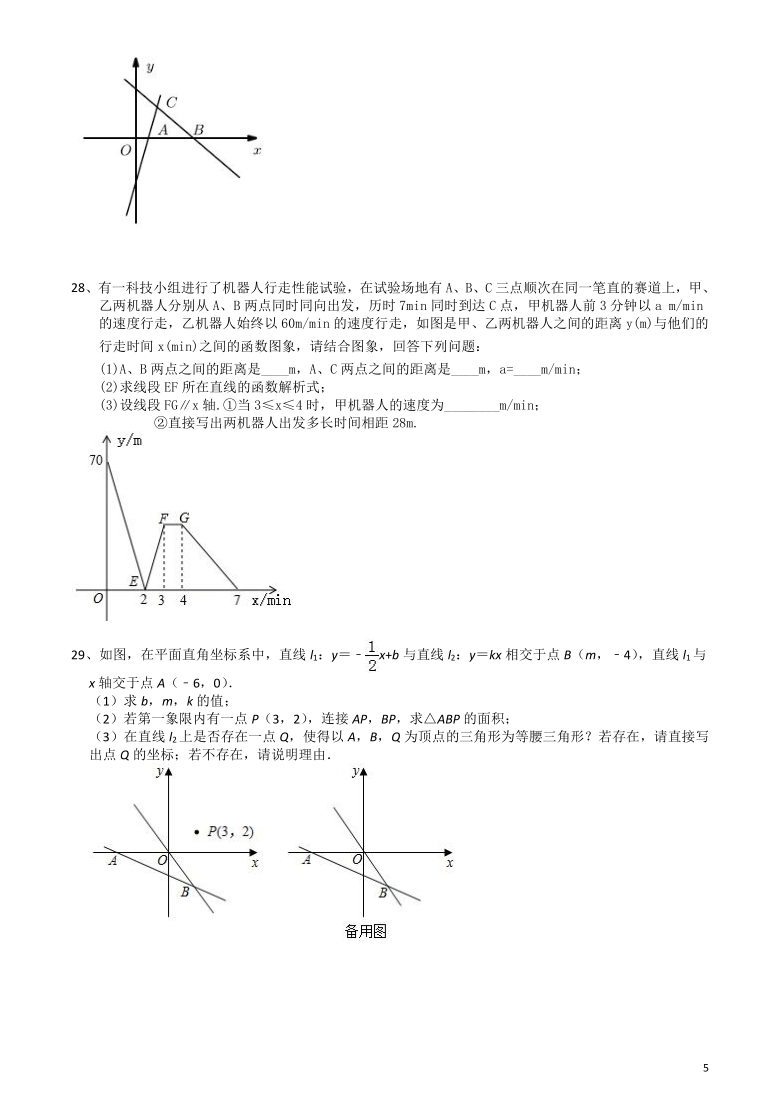
B.-2
C.±2
D.
4、已知点A(-2,y1)和点B(1,y2)是如图所示的一次函数y=2x+b图象上的两点,
则y1与y2的大小关系是(
)
A.y1<y2
B.y1>y2
C.y1=y2
D.y1≥y2
5、某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲,乙两仓库的快件数量(件)与时间(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为(
)
A.9:15
B.9:20
C.9:25
D.9:30
6、在平面直角坐标系中,将直线l1:y=-2x-2平移后,得到直线l2:y=-2x+4,
则下列平移作法正确的是(
)
A.将l1向右平移3个单位长度
B.将l1向右平移6个单位长度
C.将l1向上平移2个单位长度
D.将l1向上平移4个单位长度
7、在平面直角坐标系中,已知一次函数y=(k-2)x-b的图象大致如图所示,
则下列结论正确的是(
)
A.k>2,b>0
B.k>2,b<0
C.k<2,b>0
D.k<2,b<0
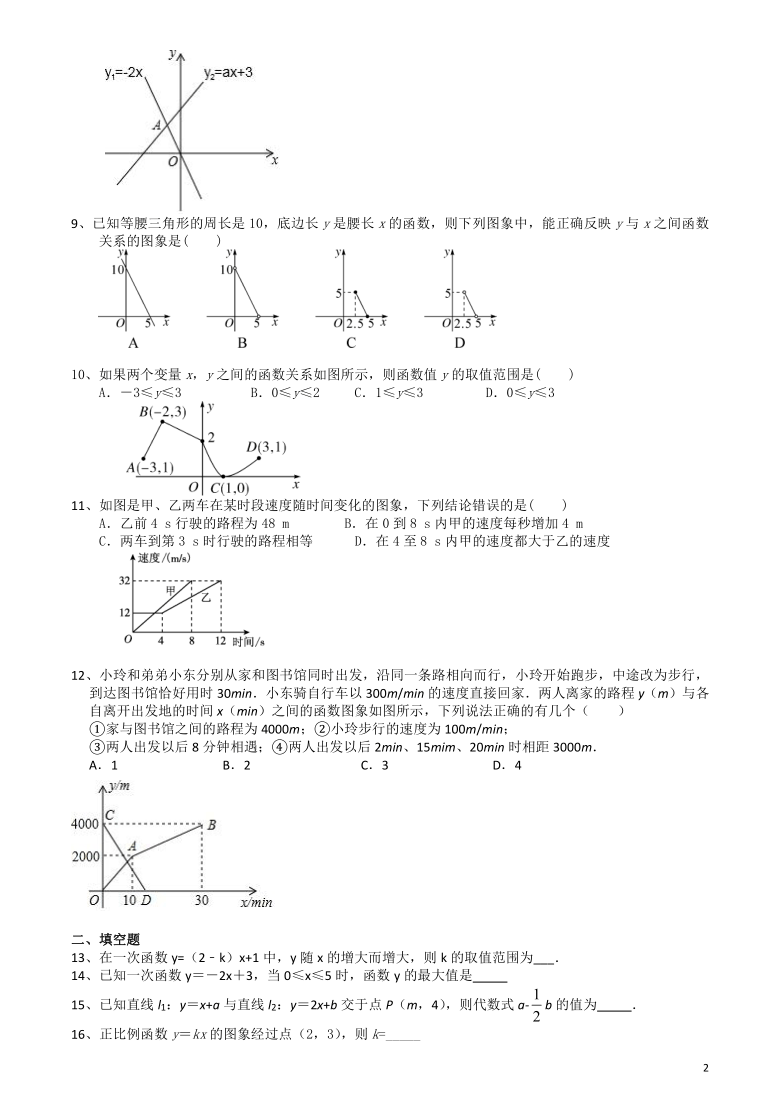
8、如图,函数
y1=﹣2x
与
y2=ax+3
的图象相交于点
A(m,2),
则关于
x
的不等式﹣2x>ax+3
的解集是(
)
A.x>2
B.x<2
C.x>﹣1
D.x<﹣1
9、已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是( )
10、如果两个变量x,y之间的函数关系如图所示,则函数值y的取值范围是( )
A.-3≤y≤3
B.0≤y≤2
C.1≤y≤3
D.0≤y≤3
11、如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.乙前4
s行驶的路程为48
m
B.在0到8
s内甲的速度每秒增加4
m
C.两车到第3
s时行驶的路程相等
D.在4至8
s内甲的速度都大于乙的速度
12、小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步,中途改为步行,到达图书馆恰好用时30min.小东骑自行车以300m/min的速度直接回家.两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示,下列说法正确的有几个( )
①家与图书馆之间的路程为4000m;②小玲步行的速度为100m/min;
③两人出发以后8分钟相遇;④两人出发以后2min、15mim、20min时相距3000m.
A.1
B.2
C.3
D.4
二、填空题
13、在一次函数y=(2﹣k)x+1中,y随x的增大而增大,则k的取值范围为___.
14、已知一次函数y=-2x+3,当0≤x≤5时,函数y的最大值是
15、已知直线l1:y=x+a与直线l2:y=2x+b交于点P(m,4),则代数式a-b的值为
.
16、正比例函数y=kx的图象经过点(2,3),则k=_____
17、如图所示,甲、乙两车在某时间段内速度随时间变化的图象.下列结论:
①甲的速度始终保持不变;②乙车第12秒时的速度为32米/秒;
③乙车前4秒行驶的总路程为48米.其中正确的是
.(填序号)
18、梯形的上底长是2,下底长是8,则梯形的面积y与高x之间的关系式是_______
19、如图,在平面直角坐标系中,函数的图像与的图像交于点,
则方程组的解为________.
20、复习课中,教师给出关于x的函数y=﹣2mx+m﹣1(m≠0),学生们在独立思考后,给出了5条关于这个函数的结论:①此函数是一次函数,但不可能是正比例函数;
②函数的值y随着自变量x的增大而减小;③该函数图象与y轴的交点在y轴的正半轴上;
④若函数图象与x轴交于A(a,0),则a<0.5;
⑤此函数图象与直线y=4x﹣3,y轴成的面积必小于0.5.
对于以上5个结论正确有
个.
21、含45°角的直角三角板如图放置在平面直角坐标系中,其中A(-2,0),B(0,1),
则直线BC的解析式为______.
22、如图,直线y=﹣x+8与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则直线AM的解析式是_____.
23、如图,定点A(-2,1),点B在直线y=x上,且横坐标为2,动点P在x轴上运动,
当线段PA+PB最短时,点P的坐标为
.
24、如图,一次函数y=2x﹣4与x轴交于点A,与y轴交于点E,过点A作AE的垂线交y轴于点B,
连接AB,以AB为边向上作正方形ABCD(如图所示),则点D的坐标为__________.
三、解答题
25、已知,都是方程y=kx+b的解.
(1)求k、b的值;
(2)若y的值不小于0,求x的取值范围;
(3)若﹣2≤x<1,求y的取值范围.
26、在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x轴、y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
(1)求函数y=-x+3的坐标三角形的三条边长;
(2)若函数y=-x+b(b为常数)的坐标三角形的周长为16,求此三角形的面积.
27、如图,已知直线:与直线:的图象的交于点,且点(2,).直线
与轴交于点,直线于轴交于点.
(1)求的值及直线的解析式.
(2)求的面积.
(3)在直线上存在点,使得的面积是的面积的2倍,请求出点的坐标.
28、有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7min同时到达C点,甲机器人前3分钟以a
m/min的速度行走,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的函数图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是____m,A、C两点之间的距离是____m,a=____m/min;
(2)求线段EF所在直线的函数解析式;
(3)设线段FG∥x轴.①当3≤x≤4时,甲机器人的速度为________m/min;
②直接写出两机器人出发多长时间相距28m.
29、如图,在平面直角坐标系中,直线l1:y=﹣x+b与直线l2:y=kx相交于点B(m,﹣4),直线l1与x轴交于点A(﹣6,0).
(1)求b,m,k的值;
(2)若第一象限内有一点P(3,2),连接AP,BP,求△ABP的面积;
(3)在直线l2上是否存在一点Q,使得以A,B,Q为顶点的三角形为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
2020-2021苏科版八年级上学期数学第6章一次函数
章末培优训练卷(1)(答案)
一、选择题
1、函数y=2+中自变量x的取值范围是( )
A.x≥2
B.x
C.x
D.x
【解析】由题意得,3x﹣1≥0,解得,x.故选:B.
2、下列函数:①y=x;②y=2x-1;③y=;④y=x2-1中,是一次函数的有(C
)
A.4个
B.3个
C.2个
D.1个
3、若是一次函数,则m的值为(
)
A.2
B.-2
C.±2
D.
【解析】解:依题意得:5-m2=1且m+2≠0,解得m=2.故选:A.
4、已知点A(-2,y1)和点B(1,y2)是如图所示的一次函数y=2x+b图象上的两点,
则y1与y2的大小关系是(A
)
A.y1<y2
B.y1>y2
C.y1=y2
D.y1≥y2
5、某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲,乙两仓库的快件数量(件)与时间(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为(
)
A.9:15
B.9:20
C.9:25
D.9:30
【解析】设甲仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y1=k1x+40,
根据题意得60k1+40=400,解得k1=6,∴y1=6x+40;
设乙仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y2=k2x+240,
根据题意得60k2+240=0,解得k2=-4,∴y2=-4x+240,
联立,解得,∴此刻的时间为9:20.故选B.
6、在平面直角坐标系中,将直线l1:y=-2x-2平移后,得到直线l2:y=-2x+4,
则下列平移作法正确的是(A
)
A.将l1向右平移3个单位长度
B.将l1向右平移6个单位长度
C.将l1向上平移2个单位长度
D.将l1向上平移4个单位长度
7、在平面直角坐标系中,已知一次函数y=(k-2)x-b的图象大致如图所示,
则下列结论正确的是(C
)
A.k>2,b>0
B.k>2,b<0
C.k<2,b>0
D.k<2,b<0
8、如图,函数
y1=﹣2x
与
y2=ax+3
的图象相交于点
A(m,2),
则关于
x
的不等式﹣2x>ax+3
的解集是(
)
A.x>2
B.x<2
C.x>﹣1
D.x<﹣1
【解析】因为函数与的图象相交于点A(m,2),把点A代入可求出,
所以点A(-1,2),然后把点A代入解得,
不等式,
可化为,解不等式可得:,故选D.
9、已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是( D )
10、如果两个变量x,y之间的函数关系如图所示,则函数值y的取值范围是( D )
A.-3≤y≤3
B.0≤y≤2
C.1≤y≤3
D.0≤y≤3
11、如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( C )
A.乙前4
s行驶的路程为48
m
B.在0到8
s内甲的速度每秒增加4
m
C.两车到第3
s时行驶的路程相等
D.在4至8
s内甲的速度都大于乙的速度
12、小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步,中途改为步行,到达图书馆恰好用时30min.小东骑自行车以300m/min的速度直接回家.两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示,下列说法正确的有几个( )
①家与图书馆之间的路程为4000m;②小玲步行的速度为100m/min;
③两人出发以后8分钟相遇;④两人出发以后2min、15mim、20min时相距3000m.
A.1
B.2
C.3
D.4
【解析】图象过(0,4000),因此家与图书馆之间的路程为4000m,因此①正确,
小玲步行的速度为(4000﹣2000)÷(30﹣10)=100m/min;因此②正确,
小玲跑步的速度为2000÷10=200m/min;相遇时间为4000÷(200+300)=8分钟,因此③正确,
④家和图书馆之间的距离为4000米,两人同时出发,相向而行,两人相距3000米时,可能在相遇前、相遇后两种情况,因此两人出发以后2min、20min时相距3000m.是错误的.
故选:C.
二、填空题
13、在一次函数y=(2﹣k)x+1中,y随x的增大而增大,则k的取值范围为___.
【解析】∵在一次函数y=(2﹣k)x+1中,y随x的增大而增大,∴2﹣k>0,解得k<2.
故答案为:k<2.
14、已知一次函数y=-2x+3,当0≤x≤5时,函数y的最大值是3
15、已知直线l1:y=x+a与直线l2:y=2x+b交于点P(m,4),则代数式a-b的值为
.
【解析】把点P(m,4)分别代入y=x+a或y=2x+b得,4=m+a①,4=2m+b,
∴2=m+b②,∴①﹣②得,a-b=2,故答案为:2.
16、正比例函数y=kx的图象经过点(2,3),则k=_____
17、如图所示,甲、乙两车在某时间段内速度随时间变化的图象.下列结论:
①甲的速度始终保持不变;②乙车第12秒时的速度为32米/秒;
③乙车前4秒行驶的总路程为48米.其中正确的是
.(填序号)
【解析】由图象可知,甲的速度逐渐增大,故①说法错误;
乙车第12秒时的速度为32米/秒,故②说法正确;
乙车前4秒行驶的总路程为:12×4=48(米),故③说法正确.
故答案为:②③.
18、梯形的上底长是2,下底长是8,则梯形的面积y与高x之间的关系式是____y=5x___
19、如图,在平面直角坐标系中,函数的图像与的图像交于点,
则方程组的解为________.
【答案】
20、复习课中,教师给出关于x的函数y=﹣2mx+m﹣1(m≠0),学生们在独立思考后,给出了5条关于这个函数的结论:①此函数是一次函数,但不可能是正比例函数;
②函数的值y随着自变量x的增大而减小;③该函数图象与y轴的交点在y轴的正半轴上;
④若函数图象与x轴交于A(a,0),则a<0.5;
⑤此函数图象与直线y=4x﹣3,y轴成的面积必小于0.5.
对于以上5个结论正确有
个.
解:此函数是一次函数,当m=1时,它是正比例函数,所以①错误;
当m<0时,函数的值y
随着自变量x的增大而增大,所以②错误;
当m<1时,该函数图象与y轴的交点在y轴的负半轴上,所以③错误;
若函数图象与x轴交于A(a,0),则﹣2ma+m﹣1=0,解得a==0.5﹣,当m>0时,a<0.5,当m<0时,a>0.5,所以④错误;
此函数图象与直线y=4x﹣3的交点坐标为(,﹣1),此直线与y轴的交点坐标为(0,m﹣1),直线
y=4x﹣3与y轴的交点坐标为(0,﹣3),所以此函数图象与直线y=4x﹣3、y轴围成的面积
=?|m﹣1+3|?=?|m+2|,当m=2时,面积为1,所以⑤错误.
故答案为:0.
21、含45°角的直角三角板如图放置在平面直角坐标系中,其中A(-2,0),B(0,1),
则直线BC的解析式为______.
【解析】如图,过C作CD⊥x轴于点D.
∵∠CAB=90°,∴∠DAC+∠BAO=∠BAO+∠ABO=90°,∴∠DAC=∠ABO.
在△AOB和△CDA中,∵,∴△AOB≌△CDA(AAS).
∵A(﹣2,0),B(0,1),∴AD=BO=1,CD=AO=2,∴C(﹣3,2),设直线BC解析式为y=kx+b,∴,解得:,∴直线BC解析式为yx+1.故答案为yx+1.
22、如图,直线y=﹣x+8与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则直线AM的解析式是_____.
【解析】∵直线y=﹣x+8与x轴、y轴分别交于A、B两点,∴y=0时,x=6,则A点坐标为:(6,0),
x=0时,y=8,则B点坐标为:(0,8);∴BO=8,AO=6,∴AB==10,
∵直线AB沿AM折叠,点B恰好落在x轴上的点C处,
∴AB=AC=10,MB=MC,∴OC=AC﹣OA=10﹣6=4.
设MO=x,则MB=MC=8﹣x,在Rt△OMC中,OM2+OC2=CM2,
∴x2+42=(8﹣x)2,解得:x=3,故M点坐标为:(0,3),
设直线AM的解析式为y=kx+3,把A(6,0)代入得0=6k+3,解得k=﹣,
∴直线AM的解析式是y=﹣+3.故答案为:y=﹣+3.
23、如图,定点A(-2,1),点B在直线y=x上,且横坐标为2,动点P在x轴上运动,
当线段PA+PB最短时,点P的坐标为(-,0)
.
24、如图,一次函数y=2x﹣4与x轴交于点A,与y轴交于点E,过点A作AE的垂线交y轴于点B,
连接AB,以AB为边向上作正方形ABCD(如图所示),则点D的坐标为____(3,2)______.
三、解答题
25、已知,都是方程y=kx+b的解.
(1)求k、b的值;
(2)若y的值不小于0,求x的取值范围;
(3)若﹣2≤x<1,求y的取值范围.
【解答】解:(1)将,代入方程y=kx+b,
得:,解得;
(2)由(1)得y=2x﹣4,
∵y≥0,∴2x﹣4≥0,解得x≥2;
(3)∵﹣2≤x<1,
∴﹣4≤2x<2,
∴﹣8≤2x﹣4<﹣2,即﹣8≤y<﹣2.
26、在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x轴、y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
(1)求函数y=-x+3的坐标三角形的三条边长;
(2)若函数y=-x+b(b为常数)的坐标三角形的周长为16,求此三角形的面积.
解:(1)∵直线y=-x+3与x轴的交点坐标为(4,0),与y轴的交点坐标为(0,3),
∴坐标三角形的三条边长分别为3,4,5.
(2)直线与x轴的交点为(b,0),与y轴的交点为(0,b),
当b>0时,OA=b,OB=b,AB=b,
b+b+b=16.解得b=4.∴坐标三角形的面积为;
当b<0时,OA=-b,OB=-b,AB=-b,
-b-b-b=16.解得b=-4.
∴坐标三角形的面积为.
综上,当函数y=-x+b的坐标三角形的周长为16时,其面积为.
27、如图,已知直线:与直线:的图象的交于点,且点(2,).直线
与轴交于点,直线于轴交于点.
(1)求的值及直线的解析式.
(2)求的面积.
(3)在直线上存在点,使得的面积是的面积的2倍,请求出点的坐标.
答案:(1);;(2)6;(3)(,6)或(11,)
28、有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7min同时到达C点,甲机器人前3分钟以a
m/min的速度行走,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的函数图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是____m,A、C两点之间的距离是____m,a=____m/min;
(2)求线段EF所在直线的函数解析式;
(3)设线段FG∥x轴.①当3≤x≤4时,甲机器人的速度为________m/min;
②直接写出两机器人出发多长时间相距28m.
答案:(1)70;490;95;(2)y=35x-70;
(3)①60;②两机器人出发1.2min、2.8min或4.6min时相距28m.
29、如图,在平面直角坐标系中,直线l1:y=﹣x+b与直线l2:y=kx相交于点B(m,﹣4),直线l1与x轴交于点A(﹣6,0).
(1)求b,m,k的值;
(2)若第一象限内有一点P(3,2),连接AP,BP,求△ABP的面积;
(3)在直线l2上是否存在一点Q,使得以A,B,Q为顶点的三角形为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【解答】解:(1)将点A坐标代入直线l1:0=﹣×(﹣6)+b,解得:b=﹣3,
直线l1:y=﹣x﹣3,
将点B的坐标代入上式并解得:m=2,即点B(2,﹣4),
将点B的坐标代入直线l2:y=kx并解得:k=﹣2,
直线l2:y=﹣2x,
故:b=﹣3,m=2,k=﹣2;
(2)设直线PB交x轴于点H,
由点PB的坐标,同理可得直线PB的表达式为:y=6x﹣16,
则点H(,0),
S△ABP=×AH×(yP﹣yB)=×(6+)×6=26;
(3)设点Q(n,﹣2n),
则AB2=80,BQ2=(n﹣2)2+(4﹣2n)2,AQ2=(n+6)2+4n2;
①当AB=BQ时,
即80=(n﹣2)2+(4﹣2n)2,解得:n=6或﹣2;
②当AB=AQ时,
同理可得:n=2或﹣;
③当AQ=BQ时,
同理可得:n=﹣,
综上,点Q的坐标为:(6,﹣12)或(﹣2,4)或(2,﹣4)或(﹣,)或(﹣,1).
章末培优训练卷(1)
一、选择题
1、函数y=2+中自变量x的取值范围是( )
A.x≥2
B.x
C.x
D.x
2、下列函数:①y=x;②y=2x-1;③y=;④y=x2-1中,是一次函数的有(
)
A.4个
B.3个
C.2个
D.1个
3、若是一次函数,则m的值为(
)
A.2
B.-2
C.±2
D.
4、已知点A(-2,y1)和点B(1,y2)是如图所示的一次函数y=2x+b图象上的两点,
则y1与y2的大小关系是(
)
A.y1<y2
B.y1>y2
C.y1=y2
D.y1≥y2
5、某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲,乙两仓库的快件数量(件)与时间(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为(
)
A.9:15
B.9:20
C.9:25
D.9:30
6、在平面直角坐标系中,将直线l1:y=-2x-2平移后,得到直线l2:y=-2x+4,
则下列平移作法正确的是(
)
A.将l1向右平移3个单位长度
B.将l1向右平移6个单位长度
C.将l1向上平移2个单位长度
D.将l1向上平移4个单位长度
7、在平面直角坐标系中,已知一次函数y=(k-2)x-b的图象大致如图所示,
则下列结论正确的是(
)
A.k>2,b>0
B.k>2,b<0
C.k<2,b>0
D.k<2,b<0
8、如图,函数
y1=﹣2x
与
y2=ax+3
的图象相交于点
A(m,2),
则关于
x
的不等式﹣2x>ax+3
的解集是(
)
A.x>2
B.x<2
C.x>﹣1
D.x<﹣1
9、已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是( )
10、如果两个变量x,y之间的函数关系如图所示,则函数值y的取值范围是( )
A.-3≤y≤3
B.0≤y≤2
C.1≤y≤3
D.0≤y≤3
11、如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.乙前4
s行驶的路程为48
m
B.在0到8
s内甲的速度每秒增加4
m
C.两车到第3
s时行驶的路程相等
D.在4至8
s内甲的速度都大于乙的速度
12、小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步,中途改为步行,到达图书馆恰好用时30min.小东骑自行车以300m/min的速度直接回家.两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示,下列说法正确的有几个( )
①家与图书馆之间的路程为4000m;②小玲步行的速度为100m/min;
③两人出发以后8分钟相遇;④两人出发以后2min、15mim、20min时相距3000m.
A.1
B.2
C.3
D.4
二、填空题
13、在一次函数y=(2﹣k)x+1中,y随x的增大而增大,则k的取值范围为___.
14、已知一次函数y=-2x+3,当0≤x≤5时,函数y的最大值是
15、已知直线l1:y=x+a与直线l2:y=2x+b交于点P(m,4),则代数式a-b的值为
.
16、正比例函数y=kx的图象经过点(2,3),则k=_____
17、如图所示,甲、乙两车在某时间段内速度随时间变化的图象.下列结论:
①甲的速度始终保持不变;②乙车第12秒时的速度为32米/秒;
③乙车前4秒行驶的总路程为48米.其中正确的是
.(填序号)
18、梯形的上底长是2,下底长是8,则梯形的面积y与高x之间的关系式是_______
19、如图,在平面直角坐标系中,函数的图像与的图像交于点,
则方程组的解为________.
20、复习课中,教师给出关于x的函数y=﹣2mx+m﹣1(m≠0),学生们在独立思考后,给出了5条关于这个函数的结论:①此函数是一次函数,但不可能是正比例函数;
②函数的值y随着自变量x的增大而减小;③该函数图象与y轴的交点在y轴的正半轴上;
④若函数图象与x轴交于A(a,0),则a<0.5;
⑤此函数图象与直线y=4x﹣3,y轴成的面积必小于0.5.
对于以上5个结论正确有
个.
21、含45°角的直角三角板如图放置在平面直角坐标系中,其中A(-2,0),B(0,1),
则直线BC的解析式为______.
22、如图,直线y=﹣x+8与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则直线AM的解析式是_____.
23、如图,定点A(-2,1),点B在直线y=x上,且横坐标为2,动点P在x轴上运动,
当线段PA+PB最短时,点P的坐标为
.
24、如图,一次函数y=2x﹣4与x轴交于点A,与y轴交于点E,过点A作AE的垂线交y轴于点B,
连接AB,以AB为边向上作正方形ABCD(如图所示),则点D的坐标为__________.
三、解答题
25、已知,都是方程y=kx+b的解.
(1)求k、b的值;
(2)若y的值不小于0,求x的取值范围;
(3)若﹣2≤x<1,求y的取值范围.
26、在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x轴、y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
(1)求函数y=-x+3的坐标三角形的三条边长;
(2)若函数y=-x+b(b为常数)的坐标三角形的周长为16,求此三角形的面积.
27、如图,已知直线:与直线:的图象的交于点,且点(2,).直线
与轴交于点,直线于轴交于点.
(1)求的值及直线的解析式.
(2)求的面积.
(3)在直线上存在点,使得的面积是的面积的2倍,请求出点的坐标.
28、有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7min同时到达C点,甲机器人前3分钟以a
m/min的速度行走,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的函数图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是____m,A、C两点之间的距离是____m,a=____m/min;
(2)求线段EF所在直线的函数解析式;
(3)设线段FG∥x轴.①当3≤x≤4时,甲机器人的速度为________m/min;
②直接写出两机器人出发多长时间相距28m.
29、如图,在平面直角坐标系中,直线l1:y=﹣x+b与直线l2:y=kx相交于点B(m,﹣4),直线l1与x轴交于点A(﹣6,0).
(1)求b,m,k的值;
(2)若第一象限内有一点P(3,2),连接AP,BP,求△ABP的面积;
(3)在直线l2上是否存在一点Q,使得以A,B,Q为顶点的三角形为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
2020-2021苏科版八年级上学期数学第6章一次函数
章末培优训练卷(1)(答案)
一、选择题
1、函数y=2+中自变量x的取值范围是( )
A.x≥2
B.x
C.x
D.x
【解析】由题意得,3x﹣1≥0,解得,x.故选:B.
2、下列函数:①y=x;②y=2x-1;③y=;④y=x2-1中,是一次函数的有(C
)
A.4个
B.3个
C.2个
D.1个
3、若是一次函数,则m的值为(
)
A.2
B.-2
C.±2
D.
【解析】解:依题意得:5-m2=1且m+2≠0,解得m=2.故选:A.
4、已知点A(-2,y1)和点B(1,y2)是如图所示的一次函数y=2x+b图象上的两点,
则y1与y2的大小关系是(A
)
A.y1<y2
B.y1>y2
C.y1=y2
D.y1≥y2
5、某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲,乙两仓库的快件数量(件)与时间(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为(
)
A.9:15
B.9:20
C.9:25
D.9:30
【解析】设甲仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y1=k1x+40,
根据题意得60k1+40=400,解得k1=6,∴y1=6x+40;
设乙仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y2=k2x+240,
根据题意得60k2+240=0,解得k2=-4,∴y2=-4x+240,
联立,解得,∴此刻的时间为9:20.故选B.
6、在平面直角坐标系中,将直线l1:y=-2x-2平移后,得到直线l2:y=-2x+4,
则下列平移作法正确的是(A
)
A.将l1向右平移3个单位长度
B.将l1向右平移6个单位长度
C.将l1向上平移2个单位长度
D.将l1向上平移4个单位长度
7、在平面直角坐标系中,已知一次函数y=(k-2)x-b的图象大致如图所示,
则下列结论正确的是(C
)
A.k>2,b>0
B.k>2,b<0
C.k<2,b>0
D.k<2,b<0
8、如图,函数
y1=﹣2x
与
y2=ax+3
的图象相交于点
A(m,2),
则关于
x
的不等式﹣2x>ax+3
的解集是(
)
A.x>2
B.x<2
C.x>﹣1
D.x<﹣1
【解析】因为函数与的图象相交于点A(m,2),把点A代入可求出,
所以点A(-1,2),然后把点A代入解得,
不等式,
可化为,解不等式可得:,故选D.
9、已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是( D )
10、如果两个变量x,y之间的函数关系如图所示,则函数值y的取值范围是( D )
A.-3≤y≤3
B.0≤y≤2
C.1≤y≤3
D.0≤y≤3
11、如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( C )
A.乙前4
s行驶的路程为48
m
B.在0到8
s内甲的速度每秒增加4
m
C.两车到第3
s时行驶的路程相等
D.在4至8
s内甲的速度都大于乙的速度
12、小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步,中途改为步行,到达图书馆恰好用时30min.小东骑自行车以300m/min的速度直接回家.两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示,下列说法正确的有几个( )
①家与图书馆之间的路程为4000m;②小玲步行的速度为100m/min;
③两人出发以后8分钟相遇;④两人出发以后2min、15mim、20min时相距3000m.
A.1
B.2
C.3
D.4
【解析】图象过(0,4000),因此家与图书馆之间的路程为4000m,因此①正确,
小玲步行的速度为(4000﹣2000)÷(30﹣10)=100m/min;因此②正确,
小玲跑步的速度为2000÷10=200m/min;相遇时间为4000÷(200+300)=8分钟,因此③正确,
④家和图书馆之间的距离为4000米,两人同时出发,相向而行,两人相距3000米时,可能在相遇前、相遇后两种情况,因此两人出发以后2min、20min时相距3000m.是错误的.
故选:C.
二、填空题
13、在一次函数y=(2﹣k)x+1中,y随x的增大而增大,则k的取值范围为___.
【解析】∵在一次函数y=(2﹣k)x+1中,y随x的增大而增大,∴2﹣k>0,解得k<2.
故答案为:k<2.
14、已知一次函数y=-2x+3,当0≤x≤5时,函数y的最大值是3
15、已知直线l1:y=x+a与直线l2:y=2x+b交于点P(m,4),则代数式a-b的值为
.
【解析】把点P(m,4)分别代入y=x+a或y=2x+b得,4=m+a①,4=2m+b,
∴2=m+b②,∴①﹣②得,a-b=2,故答案为:2.
16、正比例函数y=kx的图象经过点(2,3),则k=_____
17、如图所示,甲、乙两车在某时间段内速度随时间变化的图象.下列结论:
①甲的速度始终保持不变;②乙车第12秒时的速度为32米/秒;
③乙车前4秒行驶的总路程为48米.其中正确的是
.(填序号)
【解析】由图象可知,甲的速度逐渐增大,故①说法错误;
乙车第12秒时的速度为32米/秒,故②说法正确;
乙车前4秒行驶的总路程为:12×4=48(米),故③说法正确.
故答案为:②③.
18、梯形的上底长是2,下底长是8,则梯形的面积y与高x之间的关系式是____y=5x___
19、如图,在平面直角坐标系中,函数的图像与的图像交于点,
则方程组的解为________.
【答案】
20、复习课中,教师给出关于x的函数y=﹣2mx+m﹣1(m≠0),学生们在独立思考后,给出了5条关于这个函数的结论:①此函数是一次函数,但不可能是正比例函数;
②函数的值y随着自变量x的增大而减小;③该函数图象与y轴的交点在y轴的正半轴上;
④若函数图象与x轴交于A(a,0),则a<0.5;
⑤此函数图象与直线y=4x﹣3,y轴成的面积必小于0.5.
对于以上5个结论正确有
个.
解:此函数是一次函数,当m=1时,它是正比例函数,所以①错误;
当m<0时,函数的值y
随着自变量x的增大而增大,所以②错误;
当m<1时,该函数图象与y轴的交点在y轴的负半轴上,所以③错误;
若函数图象与x轴交于A(a,0),则﹣2ma+m﹣1=0,解得a==0.5﹣,当m>0时,a<0.5,当m<0时,a>0.5,所以④错误;
此函数图象与直线y=4x﹣3的交点坐标为(,﹣1),此直线与y轴的交点坐标为(0,m﹣1),直线
y=4x﹣3与y轴的交点坐标为(0,﹣3),所以此函数图象与直线y=4x﹣3、y轴围成的面积
=?|m﹣1+3|?=?|m+2|,当m=2时,面积为1,所以⑤错误.
故答案为:0.
21、含45°角的直角三角板如图放置在平面直角坐标系中,其中A(-2,0),B(0,1),
则直线BC的解析式为______.
【解析】如图,过C作CD⊥x轴于点D.
∵∠CAB=90°,∴∠DAC+∠BAO=∠BAO+∠ABO=90°,∴∠DAC=∠ABO.
在△AOB和△CDA中,∵,∴△AOB≌△CDA(AAS).
∵A(﹣2,0),B(0,1),∴AD=BO=1,CD=AO=2,∴C(﹣3,2),设直线BC解析式为y=kx+b,∴,解得:,∴直线BC解析式为yx+1.故答案为yx+1.
22、如图,直线y=﹣x+8与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则直线AM的解析式是_____.
【解析】∵直线y=﹣x+8与x轴、y轴分别交于A、B两点,∴y=0时,x=6,则A点坐标为:(6,0),
x=0时,y=8,则B点坐标为:(0,8);∴BO=8,AO=6,∴AB==10,
∵直线AB沿AM折叠,点B恰好落在x轴上的点C处,
∴AB=AC=10,MB=MC,∴OC=AC﹣OA=10﹣6=4.
设MO=x,则MB=MC=8﹣x,在Rt△OMC中,OM2+OC2=CM2,
∴x2+42=(8﹣x)2,解得:x=3,故M点坐标为:(0,3),
设直线AM的解析式为y=kx+3,把A(6,0)代入得0=6k+3,解得k=﹣,
∴直线AM的解析式是y=﹣+3.故答案为:y=﹣+3.
23、如图,定点A(-2,1),点B在直线y=x上,且横坐标为2,动点P在x轴上运动,
当线段PA+PB最短时,点P的坐标为(-,0)
.
24、如图,一次函数y=2x﹣4与x轴交于点A,与y轴交于点E,过点A作AE的垂线交y轴于点B,
连接AB,以AB为边向上作正方形ABCD(如图所示),则点D的坐标为____(3,2)______.
三、解答题
25、已知,都是方程y=kx+b的解.
(1)求k、b的值;
(2)若y的值不小于0,求x的取值范围;
(3)若﹣2≤x<1,求y的取值范围.
【解答】解:(1)将,代入方程y=kx+b,
得:,解得;
(2)由(1)得y=2x﹣4,
∵y≥0,∴2x﹣4≥0,解得x≥2;
(3)∵﹣2≤x<1,
∴﹣4≤2x<2,
∴﹣8≤2x﹣4<﹣2,即﹣8≤y<﹣2.
26、在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x轴、y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
(1)求函数y=-x+3的坐标三角形的三条边长;
(2)若函数y=-x+b(b为常数)的坐标三角形的周长为16,求此三角形的面积.
解:(1)∵直线y=-x+3与x轴的交点坐标为(4,0),与y轴的交点坐标为(0,3),
∴坐标三角形的三条边长分别为3,4,5.
(2)直线与x轴的交点为(b,0),与y轴的交点为(0,b),
当b>0时,OA=b,OB=b,AB=b,
b+b+b=16.解得b=4.∴坐标三角形的面积为;
当b<0时,OA=-b,OB=-b,AB=-b,
-b-b-b=16.解得b=-4.
∴坐标三角形的面积为.
综上,当函数y=-x+b的坐标三角形的周长为16时,其面积为.
27、如图,已知直线:与直线:的图象的交于点,且点(2,).直线
与轴交于点,直线于轴交于点.
(1)求的值及直线的解析式.
(2)求的面积.
(3)在直线上存在点,使得的面积是的面积的2倍,请求出点的坐标.
答案:(1);;(2)6;(3)(,6)或(11,)
28、有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7min同时到达C点,甲机器人前3分钟以a
m/min的速度行走,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的函数图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是____m,A、C两点之间的距离是____m,a=____m/min;
(2)求线段EF所在直线的函数解析式;
(3)设线段FG∥x轴.①当3≤x≤4时,甲机器人的速度为________m/min;
②直接写出两机器人出发多长时间相距28m.
答案:(1)70;490;95;(2)y=35x-70;
(3)①60;②两机器人出发1.2min、2.8min或4.6min时相距28m.
29、如图,在平面直角坐标系中,直线l1:y=﹣x+b与直线l2:y=kx相交于点B(m,﹣4),直线l1与x轴交于点A(﹣6,0).
(1)求b,m,k的值;
(2)若第一象限内有一点P(3,2),连接AP,BP,求△ABP的面积;
(3)在直线l2上是否存在一点Q,使得以A,B,Q为顶点的三角形为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【解答】解:(1)将点A坐标代入直线l1:0=﹣×(﹣6)+b,解得:b=﹣3,
直线l1:y=﹣x﹣3,
将点B的坐标代入上式并解得:m=2,即点B(2,﹣4),
将点B的坐标代入直线l2:y=kx并解得:k=﹣2,
直线l2:y=﹣2x,
故:b=﹣3,m=2,k=﹣2;
(2)设直线PB交x轴于点H,
由点PB的坐标,同理可得直线PB的表达式为:y=6x﹣16,
则点H(,0),
S△ABP=×AH×(yP﹣yB)=×(6+)×6=26;
(3)设点Q(n,﹣2n),
则AB2=80,BQ2=(n﹣2)2+(4﹣2n)2,AQ2=(n+6)2+4n2;
①当AB=BQ时,
即80=(n﹣2)2+(4﹣2n)2,解得:n=6或﹣2;
②当AB=AQ时,
同理可得:n=2或﹣;
③当AQ=BQ时,
同理可得:n=﹣,
综上,点Q的坐标为:(6,﹣12)或(﹣2,4)或(2,﹣4)或(﹣,)或(﹣,1).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
