18.1.1 第2课时 平行四边形的对角线的特征 课件(共43张PPT)
文档属性
| 名称 | 18.1.1 第2课时 平行四边形的对角线的特征 课件(共43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 00:00:00 | ||
图片预览


文档简介
(共43张PPT)
第十八章
平行四边形
18.1.1
平行四边形的性质
第2课时
平行四边形的对角线的特征
人教版
八年级数学下册
教学课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
情景导学
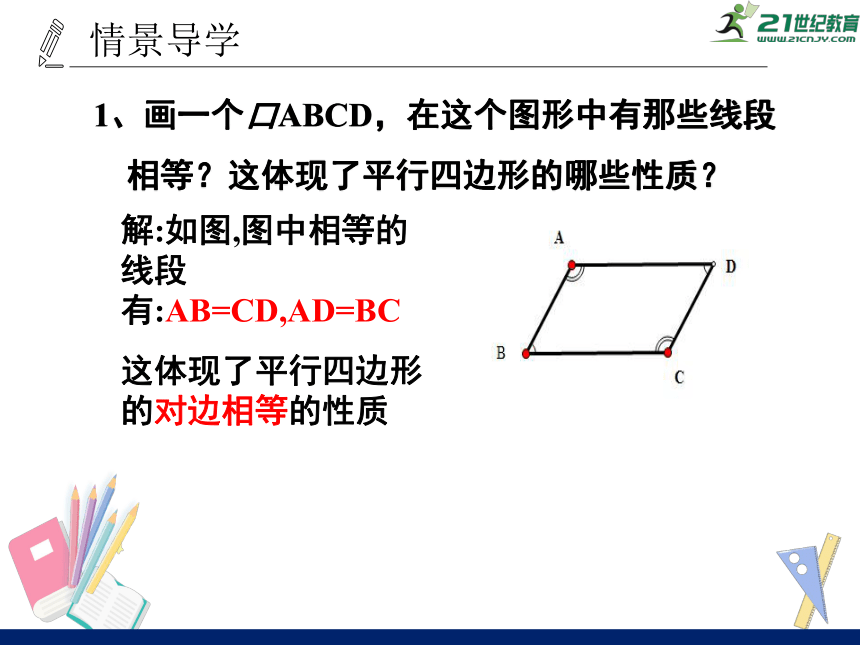
1、画一个口ABCD,在这个图形中有那些线段
相等?这体现了平行四边形的哪些性质?
解:如图,图中相等的线段有:AB=CD,AD=BC
这体现了平行四边形的对边相等的性质
情景导学
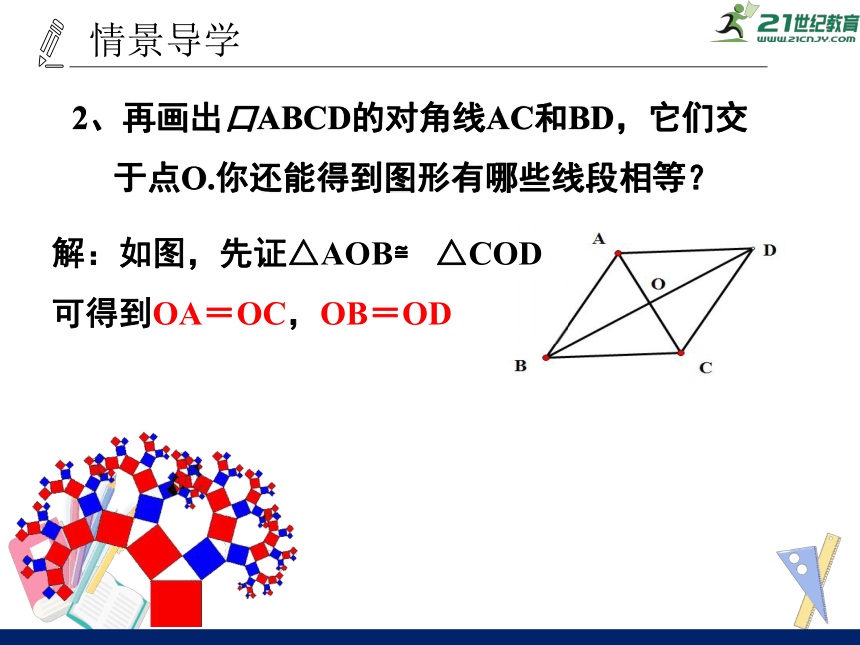
2、再画出口ABCD的对角线AC和BD,它们交
于点O.你还能得到图形有哪些线段相等?
解:如图,先证△AOB≌
△COD
可得到OA=OC,OB=OD
情景导学
一位饱经沧桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
当四个孩子看到时,争论不休,都认为自己分的地少,同学们,你认为老人这样分合理吗?为什么?
第二部分
新课目标
新课目标
平行四
边形对角线的
性质
平行四边形对角线互相平分
两条对角线分平行四边形为面积相等的四个三角形
过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等.
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分.且与对角线围成的三角形相对的两个全等.
第三部分
新课进行时
新课进行时
核心知识点一
平行四边形的对角线的性质
我们知道平行四边形的边角这两个基本要素的性质,那么平行四边形的对角线又具有怎样的性质呢?
A
B
C
D
O
如图,在□ABCD中,连接AC,BD,并设它们相交于点O.
OA与OC,OB与OD有什么关系?
猜一猜
OA=OC,OB=OD
怎样证明这个猜想呢?
新课进行时
已知:如图,□
ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴
AD=BC,AD∥BC,
∴
∠1=∠2,∠3=∠4,
∴
△AOD≌△COB(ASA),
∴
OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
新课进行时
A
C
D
B
O
平行四边形的对角线互相平分.
应用格式:
∵四边形ABCD是平行四边形,
∴
OA=OC,OB=OD.
平行四边形的性质
新课进行时
已知:如图,在口ABCD中,对角线AC,BD
交于点O.求证:OA=
,OB=
.
证明:∵四边形ABCD是平行四边形,
∴AB∥_____,AB=_____(平行四边形的性质)
∴∠1=∠2,
∠3=∠4(
)
在△AOB和△COD中
____________
____________
____________
∴_________________(
)
∴OA=
,OB=
.(全等三角形的对应边相等)
OD
OC
CD
CD
两直线平行,内错角相等
∠2=
∠1
∠4=
∠3
AB=CD
△AOB≌△COD
ASA
OC
OD
新课进行时
例1
已知
ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,求这个平行四边形各边的长.
解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC.
∵△AOB的周长比△DOA的周长长5cm,
∴AB-AD=5cm.
又∵
ABCD的周长为60cm,∴AB+AD=30cm,
则AB=CD=17.5cm,AD=BC=12.5cm.
平行四边形被对角线分成四个小三角形,相邻两个三角形的周长之差等于邻边边长之差.
归纳
新课进行时
【变式题】如图,在平行四边形ABCD中,对角线AC、BD相交于点O,平行四边形ABCD的周长是100cm,△AOB与△BOC的周长的和是122cm,且AC:DB=
2:1,求AC和BD的长.
解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,OB=OD,
∴AB+BC=50.
∵△AOB与△BOC的周长的和是122cm,
∴OA+OB+AB+OB+OC+BC=122,
即AC+BD=122-50=72.
又∵AC:DB=2:1,
∴AC=48cm,BD=24cm.
新课进行时
例2
如图,平行四边形ABCD中,AC、BD交于O点,点E、F分别是AO、CO的中点,试判断线段BE、DF的关系并证明你的结论.
解:BE=DF,BE∥DF.
理由如下:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴OE=OF.
在△OFD和△OEB中,
OE=OF,∠DOF=∠BOE,OD=OB,
∴△OFD≌△OEB,
∴∠OEB=∠OFD,BE=DF,
∴BE∥DF.
新课进行时
例3
如图,
ABCD的对角线AC,BD交于点O.点O作直线EF,分别交AB,CD于点E,F.求证:OE=OF.
A
B
C
D
F
E
O
证明:∵四边形ABCD是平行四边形,
∴∠ODF=∠OBE,
∠DFO=∠BEO,
∴△DOF≌△BOE(AAS),
∴AB∥CD,
OD=OB,
∴OE=OF.
思考
改变直线EF的位置,OE=OF还成立吗?
新课进行时
A
B
C
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
请判断下列图中,OE=OF还成立么?
同例3易证明OE=OF还成立.
过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等.
归纳
新课进行时
1.如图,平行四边形ABCD的对角线AC,BD交于点O,若AD=16,AC=24,BD=12,则△OBC的周长为
( )
A.26
B.34
C.40
D.52
B
新课进行时
2.如图,在?ABCD中,对角线AC和BD相交于点O,△AOB的周长为15,AB=6,则对角线AC、BD的长度的和是
( )
A.9
B.18
C.27
D.36
B
新课进行时
A
B
C
D
O
解:∵四边形ABCD是平行四边形,
根据勾股定理得
∴BC=AD=8,CD=AB=10.
是直角三角形.
又∵OA=OC,
例4 如图,在 ABCD中,AB=10,AD=8,AC⊥
BC.
求BC,CD,AC,OA的长,以及 ABCD的面积.
新课进行时
例5
如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若平行四边形ABCD的周长为48,DE=5,DF=10,求平行四边形ABCD的面积.
解:设AB=x,则BC=24-x.
根据平行四边形的面积公式可得5x=10(24-x),
解得x=16.
则平行四边形ABCD的面积为5×16=80.
已知平行四边形的高DE,DF,根据“等面积法”及平行四边形的性质列方程求解.
归纳
新课进行时
平行四边形的对角线分平行四边形ABCD为四个三角形,它们的面积有怎样的关系呢?
解:相等.理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵△ADO与△ODC等底同高,
∴S△ADO=S△ODC.
同理可得S△ADO=S△ODC=S△BCO=S△AOB.
还可结合全等来证哟.
平行四边形的对角线分平行四边形为四个面积相等的三角形,且都等于平行四边形面积的四分之一.相对的两个三角形全等.
归纳
新课进行时
A
B
C
D
O
F
E
例6
如图,AC,BD交于点O,EF过点O,平行四边形ABCD被EF所分的两个四边形面积相等吗?
M
N
解:设直线EF交AD,BC于点N,M.
∵AD∥BC,
∴∠NAO=∠MCO,∠ANO=∠CMO.
又∵AO=CO,
∴△NAO≌△MCO,
∴S四边形ANMB=S△NAO+S△AOB+S△MOB=S△MCO+S△AOB+S△MOB
=S△AOB+S△COB=
.
∴S四边形ANMB=S四边形CMND,
即平行四边形ABCD被EF所分的两个四边形面积相等.
新课进行时
A
B
D
O
E
F
A
B
C
D
O
E
F
C
A
B
C
D
O
E
F
思考
如图,AC,BD交于点O,EF过点O,平行四边形ABCD被EF所分的两个四边形面积相等吗?
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分.
归纳
同例5易求得平行四边形ABCD被EF所分的两个四边形面积相等.
第四部分
知识小结
知识小结
1.一元一次不等式的定义和性质
2.一元一次不等式的解法及应用
3.一元一次不等式组的定义、解集及应用
第五部分
随堂演练
随堂演练
解:(9+12)×2
=21×2
=42(cm2)
答:平行四边形的面积是42cm2.
1.把一个平行四边形分成3个三角形,已知两个阴影三角形的面积分别是9cm2和12cm2,求平行四边形的面积.
随堂演练
2.如图,欢欢看到平行四边形的草地中间有一水井,为了浇水的方便,欢欢建议我们经过水井修小路,一样可以把草地分成面积相等的两部分,同学们,你知道聪明的欢欢是怎么分的吗?
B
M
C
●
D
A
O
解:如图所示.
随堂演练
1.如图,□ABCD的对角线AC、BD相交于点O,且
AC+BD=16,CD=6,则△ABO的周长是(
)
A.
10
B.
14
C.
20
D.
22
B
B
C
D
A
O
随堂演练
2.如图,在平行四边形ABCD中,下列结论中错误的是( )
A.∠ABO=∠CDO
B.∠BAD=∠BCD
C.AO=CO
D.AC⊥BD
B
C
D
A
O
D
随堂演练
3.在□ABCD中,AC=24,BD=38,AB=m,
则m的取值范围是
(
)
A.
24B.14C.7D.7B
C
D
A
O
C
随堂演练
4.如图,?ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于E,F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为( )
A.16
B.14
C.12
D.10
A
D
C
B
F
E
O
C
随堂演练
5.如图,平行四边形ABCD的面积为20,对角线AC,BD相交于点O,点E,F分别是AB,CD上的点,且AE=DF,则图中阴影部分的面积为_______.
5
随堂演练
6.如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,则BD的长是
.
随堂演练
7.如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E.若△CDE的周长为10,则平行四边形ABCD的周长是多少?
解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,OB=OD.
∵OE⊥BD,
∴BE=DE.
∵△CDE的周长为10,
∴DE+CE+CD=BE+CE+CD=BC+CD=10,
∴平行四边形ABCD的周长为
2×(BC+CD)=20.
随堂演练
8.如图,已知O是平行四边形ABCD的对角线的交点,AC=24,BD=18,AB=16,求△OCD的周长及AD边的取值范围.
解:由题意得OA=OC=12,OB=OD=9,CD=AB=16,
∴△OCD的周长为12+9+16=37.
在△ACD中,24-16<AD<24+16,∴8<AD<40;
在△ABD中,18-16<AD<18+16,∴2<AD<34;
在△AOD中,12-9<AD<12+9,∴3<AD<21.
综上所述,AD的取值范围应是8<AD<21.
与三角形三边关系结合
随堂演练
3、在口ABCD中,AC和BD交于点O,AB=4,△AOB的周长为16,求AC+BD的长度.
解∵
=16,AB=4
∴OA+OB=16-4=12
∵四边形ABCD是平行四边形
∴AC=2OA,BD=2OB
∴AC+BD=2OA+2OB
=2(OA+OB)
=2×12=24
第六部分
课后作业
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
第十八章
平行四边形
18.1.1
平行四边形的性质
第2课时
平行四边形的对角线的特征
人教版
八年级数学下册
教学课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
情景导学
1、画一个口ABCD,在这个图形中有那些线段
相等?这体现了平行四边形的哪些性质?
解:如图,图中相等的线段有:AB=CD,AD=BC
这体现了平行四边形的对边相等的性质
情景导学
2、再画出口ABCD的对角线AC和BD,它们交
于点O.你还能得到图形有哪些线段相等?
解:如图,先证△AOB≌
△COD
可得到OA=OC,OB=OD
情景导学
一位饱经沧桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
当四个孩子看到时,争论不休,都认为自己分的地少,同学们,你认为老人这样分合理吗?为什么?
第二部分
新课目标
新课目标
平行四
边形对角线的
性质
平行四边形对角线互相平分
两条对角线分平行四边形为面积相等的四个三角形
过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等.
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分.且与对角线围成的三角形相对的两个全等.
第三部分
新课进行时
新课进行时
核心知识点一
平行四边形的对角线的性质
我们知道平行四边形的边角这两个基本要素的性质,那么平行四边形的对角线又具有怎样的性质呢?
A
B
C
D
O
如图,在□ABCD中,连接AC,BD,并设它们相交于点O.
OA与OC,OB与OD有什么关系?
猜一猜
OA=OC,OB=OD
怎样证明这个猜想呢?
新课进行时
已知:如图,□
ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴
AD=BC,AD∥BC,
∴
∠1=∠2,∠3=∠4,
∴
△AOD≌△COB(ASA),
∴
OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
新课进行时
A
C
D
B
O
平行四边形的对角线互相平分.
应用格式:
∵四边形ABCD是平行四边形,
∴
OA=OC,OB=OD.
平行四边形的性质
新课进行时
已知:如图,在口ABCD中,对角线AC,BD
交于点O.求证:OA=
,OB=
.
证明:∵四边形ABCD是平行四边形,
∴AB∥_____,AB=_____(平行四边形的性质)
∴∠1=∠2,
∠3=∠4(
)
在△AOB和△COD中
____________
____________
____________
∴_________________(
)
∴OA=
,OB=
.(全等三角形的对应边相等)
OD
OC
CD
CD
两直线平行,内错角相等
∠2=
∠1
∠4=
∠3
AB=CD
△AOB≌△COD
ASA
OC
OD
新课进行时
例1
已知
ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,求这个平行四边形各边的长.
解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC.
∵△AOB的周长比△DOA的周长长5cm,
∴AB-AD=5cm.
又∵
ABCD的周长为60cm,∴AB+AD=30cm,
则AB=CD=17.5cm,AD=BC=12.5cm.
平行四边形被对角线分成四个小三角形,相邻两个三角形的周长之差等于邻边边长之差.
归纳
新课进行时
【变式题】如图,在平行四边形ABCD中,对角线AC、BD相交于点O,平行四边形ABCD的周长是100cm,△AOB与△BOC的周长的和是122cm,且AC:DB=
2:1,求AC和BD的长.
解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,OB=OD,
∴AB+BC=50.
∵△AOB与△BOC的周长的和是122cm,
∴OA+OB+AB+OB+OC+BC=122,
即AC+BD=122-50=72.
又∵AC:DB=2:1,
∴AC=48cm,BD=24cm.
新课进行时
例2
如图,平行四边形ABCD中,AC、BD交于O点,点E、F分别是AO、CO的中点,试判断线段BE、DF的关系并证明你的结论.
解:BE=DF,BE∥DF.
理由如下:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴OE=OF.
在△OFD和△OEB中,
OE=OF,∠DOF=∠BOE,OD=OB,
∴△OFD≌△OEB,
∴∠OEB=∠OFD,BE=DF,
∴BE∥DF.
新课进行时
例3
如图,
ABCD的对角线AC,BD交于点O.点O作直线EF,分别交AB,CD于点E,F.求证:OE=OF.
A
B
C
D
F
E
O
证明:∵四边形ABCD是平行四边形,
∴∠ODF=∠OBE,
∠DFO=∠BEO,
∴△DOF≌△BOE(AAS),
∴AB∥CD,
OD=OB,
∴OE=OF.
思考
改变直线EF的位置,OE=OF还成立吗?
新课进行时
A
B
C
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
请判断下列图中,OE=OF还成立么?
同例3易证明OE=OF还成立.
过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等.
归纳
新课进行时
1.如图,平行四边形ABCD的对角线AC,BD交于点O,若AD=16,AC=24,BD=12,则△OBC的周长为
( )
A.26
B.34
C.40
D.52
B
新课进行时
2.如图,在?ABCD中,对角线AC和BD相交于点O,△AOB的周长为15,AB=6,则对角线AC、BD的长度的和是
( )
A.9
B.18
C.27
D.36
B
新课进行时
A
B
C
D
O
解:∵四边形ABCD是平行四边形,
根据勾股定理得
∴BC=AD=8,CD=AB=10.
是直角三角形.
又∵OA=OC,
例4 如图,在 ABCD中,AB=10,AD=8,AC⊥
BC.
求BC,CD,AC,OA的长,以及 ABCD的面积.
新课进行时
例5
如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若平行四边形ABCD的周长为48,DE=5,DF=10,求平行四边形ABCD的面积.
解:设AB=x,则BC=24-x.
根据平行四边形的面积公式可得5x=10(24-x),
解得x=16.
则平行四边形ABCD的面积为5×16=80.
已知平行四边形的高DE,DF,根据“等面积法”及平行四边形的性质列方程求解.
归纳
新课进行时
平行四边形的对角线分平行四边形ABCD为四个三角形,它们的面积有怎样的关系呢?
解:相等.理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵△ADO与△ODC等底同高,
∴S△ADO=S△ODC.
同理可得S△ADO=S△ODC=S△BCO=S△AOB.
还可结合全等来证哟.
平行四边形的对角线分平行四边形为四个面积相等的三角形,且都等于平行四边形面积的四分之一.相对的两个三角形全等.
归纳
新课进行时
A
B
C
D
O
F
E
例6
如图,AC,BD交于点O,EF过点O,平行四边形ABCD被EF所分的两个四边形面积相等吗?
M
N
解:设直线EF交AD,BC于点N,M.
∵AD∥BC,
∴∠NAO=∠MCO,∠ANO=∠CMO.
又∵AO=CO,
∴△NAO≌△MCO,
∴S四边形ANMB=S△NAO+S△AOB+S△MOB=S△MCO+S△AOB+S△MOB
=S△AOB+S△COB=
.
∴S四边形ANMB=S四边形CMND,
即平行四边形ABCD被EF所分的两个四边形面积相等.
新课进行时
A
B
D
O
E
F
A
B
C
D
O
E
F
C
A
B
C
D
O
E
F
思考
如图,AC,BD交于点O,EF过点O,平行四边形ABCD被EF所分的两个四边形面积相等吗?
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分.
归纳
同例5易求得平行四边形ABCD被EF所分的两个四边形面积相等.
第四部分
知识小结
知识小结
1.一元一次不等式的定义和性质
2.一元一次不等式的解法及应用
3.一元一次不等式组的定义、解集及应用
第五部分
随堂演练
随堂演练
解:(9+12)×2
=21×2
=42(cm2)
答:平行四边形的面积是42cm2.
1.把一个平行四边形分成3个三角形,已知两个阴影三角形的面积分别是9cm2和12cm2,求平行四边形的面积.
随堂演练
2.如图,欢欢看到平行四边形的草地中间有一水井,为了浇水的方便,欢欢建议我们经过水井修小路,一样可以把草地分成面积相等的两部分,同学们,你知道聪明的欢欢是怎么分的吗?
B
M
C
●
D
A
O
解:如图所示.
随堂演练
1.如图,□ABCD的对角线AC、BD相交于点O,且
AC+BD=16,CD=6,则△ABO的周长是(
)
A.
10
B.
14
C.
20
D.
22
B
B
C
D
A
O
随堂演练
2.如图,在平行四边形ABCD中,下列结论中错误的是( )
A.∠ABO=∠CDO
B.∠BAD=∠BCD
C.AO=CO
D.AC⊥BD
B
C
D
A
O
D
随堂演练
3.在□ABCD中,AC=24,BD=38,AB=m,
则m的取值范围是
(
)
A.
24
C
D
A
O
C
随堂演练
4.如图,?ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于E,F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为( )
A.16
B.14
C.12
D.10
A
D
C
B
F
E
O
C
随堂演练
5.如图,平行四边形ABCD的面积为20,对角线AC,BD相交于点O,点E,F分别是AB,CD上的点,且AE=DF,则图中阴影部分的面积为_______.
5
随堂演练
6.如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,则BD的长是
.
随堂演练
7.如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E.若△CDE的周长为10,则平行四边形ABCD的周长是多少?
解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,OB=OD.
∵OE⊥BD,
∴BE=DE.
∵△CDE的周长为10,
∴DE+CE+CD=BE+CE+CD=BC+CD=10,
∴平行四边形ABCD的周长为
2×(BC+CD)=20.
随堂演练
8.如图,已知O是平行四边形ABCD的对角线的交点,AC=24,BD=18,AB=16,求△OCD的周长及AD边的取值范围.
解:由题意得OA=OC=12,OB=OD=9,CD=AB=16,
∴△OCD的周长为12+9+16=37.
在△ACD中,24-16<AD<24+16,∴8<AD<40;
在△ABD中,18-16<AD<18+16,∴2<AD<34;
在△AOD中,12-9<AD<12+9,∴3<AD<21.
综上所述,AD的取值范围应是8<AD<21.
与三角形三边关系结合
随堂演练
3、在口ABCD中,AC和BD交于点O,AB=4,△AOB的周长为16,求AC+BD的长度.
解∵
=16,AB=4
∴OA+OB=16-4=12
∵四边形ABCD是平行四边形
∴AC=2OA,BD=2OB
∴AC+BD=2OA+2OB
=2(OA+OB)
=2×12=24
第六部分
课后作业
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
