18.2.3 第1课时 正方形的性质 课件(共37张PPT)
文档属性
| 名称 | 18.2.3 第1课时 正方形的性质 课件(共37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 00:00:00 | ||
图片预览



文档简介
(共37张PPT)
第十八章
平行四边形
18.2.3
正方形
第1课时
正方形的性质
人教版
八年级数学下册
教学课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
情景导学
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
你还能举出其他的例子吗?
情景导学
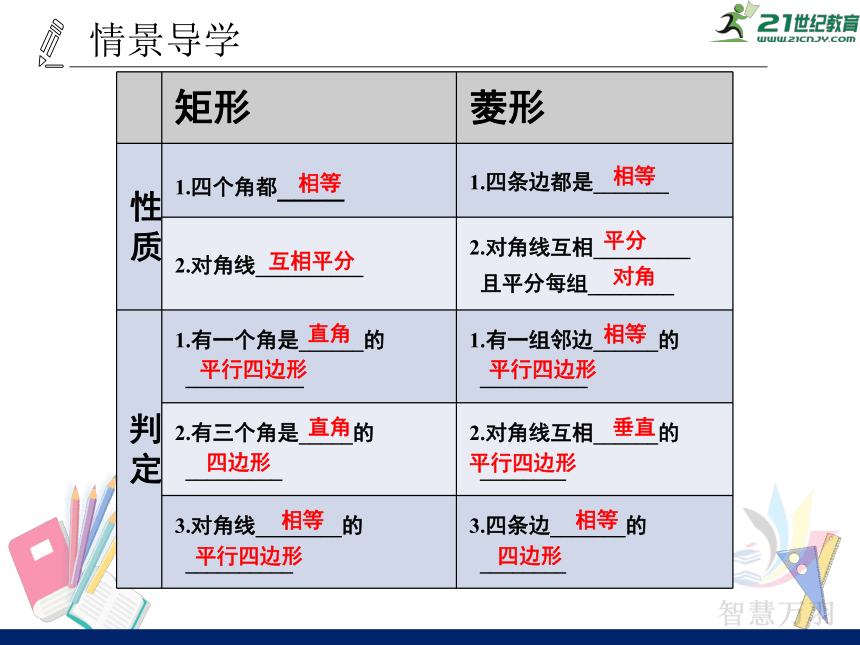
矩形
菱形
性质
1.四个角都____
1.四条边都是_______
2.对角线__________
2.对角线互相_________
且平分每组________
判定
1.有一个角是______的
___________
1.有一组邻边______的
__________
2.有三个角是_____的
_________
2.对角线互相______的
________
3.对角线________的
__________
3.四条边_______的
________
相等
直角
相等
相等
平行四边形
直角
对角
平分
相等
互相平分
平行四边形
相等
平行四边形
垂直
四边形
平行四边形
四边形
第二部分
新课目标
新课目标
1.理解正方形的概念.
2.探索并证明正方形的性质,并了解平行四边形、
矩形、菱形之间的联系和区别.(重点、难点)
3.会应用正方形的性质解决相关证明及计算问题.
(难点)
第三部分
新课进行时
新课进行时
核心知识点一
正方形的性质
矩
形
〃
〃
矩形怎样变化后就成了正方形呢?你有什么发现?
正方形
新课进行时
菱形怎样变化后就成了正方形呢?你有什么发现?
正方形
新课进行时
知识点一
正方形的定义
1、四条边_______,四个角都是_______的四边形叫做正方形.
2、正方形既是_____形,又是_____形.即
(1)有一组________相等的矩形是正方形.
(2)有一个角是________的菱形是正方形.
相等
直角
矩
菱
直角
邻边
新课进行时
已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.
A
B
C
D
证明:∵四边形ABCD是正方形.
∴∠A=90°,
AB=AC
(正方形的定义).
又∵正方形是平行四边形.
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
∴∠A=∠B
=∠C
=∠D
=
90°,
AB=
BC=CD=AD.
新课进行时
请同学们拿出准备好的正方形纸片,折一折,观察并思考.??正方形是不是轴对称图形?如果是,那么对称轴有几条?
对称性:
.
对称轴:
.
轴对称图形
4条
A
B
C
D
新课进行时
1、正方形具有_____的性质,同时又具有______的性质.
边:对边________,四边_________;
角:四个角都是________;
线:对角线相等,互相________,每条对角线平分一组________.
形:是_______________对称图形.
2、正方形与平行四边形、矩形、菱形之间的关系有怎样的包含关系?请填入下图中.
菱形
矩形
直角
都相等
相等
轴对称和中心
平分
对角
菱形
正方形
矩形
新课进行时
求证:
正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
A
D
C
B
O
已知:
如图,四边形ABCD是正方形,对角线AC、BD相
交于点O.
求证:
△ABO、
△BCO、
△CDO、
△DAO是全等
的等腰直角三角形.
证明:
∵
四边形ABCD是正方形,
∴
AC=BD,AC⊥BD,AO=BO=CO=DO.
∴
△ABO、
△BCO、
△CDO、
△DAO都
是等腰直角三角形,并且
△ABO≌
△BCO
≌
△CDO
≌
△DAO.
新课进行时
如图,在正方形ABCD中,
ΔBEC是等边三角形,
求证:
∠EAD=∠EDA=15°
.
证明:∵
ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵
四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD,
∠ABE=
∠DCE=30°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE=
∠BEA=
∠CDE=
∠CED=75°,
∴∠EAD=
∠EDA=90°-75°=15°.
新课进行时
当等边△ADE在正方形ABCD内部时,如图②,
AB=AE,∠BAE=90°-60°=30°,
∴∠AEB=75°.
同理可得∠DEC=75°.
∴∠BEC=360°-75°-75°-60°=150°.
综上所述,∠BEC的大小为30°或150°.
易错提醒:因为等边△ADE与正方形ABCD有一条公共边,所以边相等.本题分两种情况:等边△ADE在正方形的外部或在正方形的内部.
新课进行时
如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.
(1)求证:△APB≌△DPC;
解:∵四边形ABCD是正方形,
∴∠ABC=∠DCB=90°.
∵PB=PC,
∴∠PBC=∠PCB.
∴∠ABC-∠PBC=∠DCB-∠PCB,
即∠ABP=∠DCP.
又∵AB=DC,PB=PC,
∴△APB≌△DPC.
新课进行时
证明:∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°.
∵△APB≌△DPC,
∴AP=DP.
又∵AP=AB=AD,
∴DP=AP=AD.
∴△APD是等边三角形.
∴∠DAP=60°.
∴∠PAC=∠DAP-∠DAC=15°.
∴∠BAP=∠BAC-∠PAC=30°.
∴∠BAP=2∠PAC.
(2)求证:∠BAP=2∠PAC.
新课进行时
如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E,
PF⊥DC于F.试说明:AP=EF.
A
B
C
D
P
E
F
解:
连接PC,AC.
又∵PE⊥BC
,
PF⊥DC,
∵四边形ABCD是正方形,
∴∠FCE=90°,
AC垂直平分BD,
∴四边形PECF是矩形,
∴PC=EF.
∴AP=PC.
∴AP=EF.
在正方形的条件下证明两条线段相等:通常连接对角线构造垂直平分的模型,利用垂直平分线性质,角平分线性质,等腰三角形等来说明.
归纳
第四部分
知识小结
知识小结
1.四个角都是直角
2.四条边都相等
3.对角线相等且互相垂直平分
正方形的性质
性质
定义
有一组邻相等,并且有一个角是直角的平行四边形叫做正方形.
第五部分
随堂演练
随堂演练
满足下列条件的四边形是不是正方形?为什么?
(1)对角线互相垂直且相等的平行四边形;
(2)对角线互相垂直的矩形;
(3)对角线相等的菱形;
(4)对角线互相垂直平分且相等的四边形.
解:(1)根据正方形的性质可知,是正方形
(2)根据正方形的性质可知,是正方形
(3)根据正方形的性质可知,是正方形
(4)根据正方形的性质可知,是正方形
随堂演练
1.正方形具有而矩形不一定具有的性质是
(
)
A.四个角相等
B.对角线互相垂直平分
C.对角互补
D.对角线相等
2.正方形具有而菱形不一定具有的性质(
)
A.四条边相等
B.对角线互相垂直平分
C.对角线平分一组对角
D.对角线相等
B
D
随堂演练
3.如图,四边形ABCD是正方形,对角线AC与BD相交于点O,AO=2,求正方形的周长与面积.
解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OD=2.
在Rt△AOD中,由勾股定理,得
∴正方形的周长为4AD=
,
面积为AD2=8.
随堂演练
2.一个正方形的对角线长为2cm,则它的面积是
( )
A.2cm2
B.4cm2
C.6cm2
D.8cm2
A
1.平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
A
随堂演练
3.在正方形ABC中,∠ADB=
,∠DAC=
,
∠BOC=
.
4.在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是
.
A
D
B
C
O
A
D
B
C
O
E
45°
90°
22.5°
第3题图
第4题图
45°
5.如图,正方形ABCD的边长为1cm,AC为对角线,AE平分∠BAC,EF⊥AC,求BE的长.
解:∵四边形ABCD为正方形,
∴∠B=90°,∠ACB=45°,AB=BC=1cm.
∵EF⊥AC,∴∠EFA=∠EFC=90°.
又∵∠ECF=45°,
∴△EFC是等腰直角三角形,∴EF=FC.
∵∠BAE=∠FAE,∠B=∠EFA=90°,AE=AE,
∴△ABE≌△AFE,
∴AB=AF=1cm,BE=EF.
∴FC=BE.
在Rt△ABC中,
∴FC=AC-AF=(
-1)cm,
∴BE=(
-1)cm.
随堂演练
6.
如图在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF.
BE与DF之间有怎样的关系?请说明理由.
解:BE=DF,且BE⊥DF.理由如下:
∵四边形ABCD是正方形.
∴BC=DC,∠BCE
=90°
.
∴∠DCF=180°-∠BCE=90°.
∴∠BCE=∠DCF.
又∵CE=CF.
∴△BCE≌△DCF.
∴BE=DF.
A
B
D
C
F
E
随堂演练
延长BE交DE于点M,
∵△BCE≌△DCF
,
∴∠CBE
=∠CDF.
∵∠DCF
=90°
,
∴∠CDF
+∠F
=90°,
∴∠CBE+∠F=90°
,
∴∠BMF=90°.
∴BE⊥DF.
A
B
D
F
E
C
M
随堂演练
已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.
解:∵∠C=90°,DE⊥BC于E,
DF⊥AC于F
∴四边形CEDF有三个直角,
它是矩形
又∵CD平分∠ACB
根据角平分线上的点都两边的距离相等,可知DE=DF,所以矩形CEDF有一组邻边相等
根据正方形的判定方法,知四边形CEDF是正方形
随堂演练
1、根据图形所具有的性质,在下表相应的空格中打“√”
平行四边形
矩形
菱形
正方形
对边平行且相等
四边都相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
第六部分
课后作业
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
第十八章
平行四边形
18.2.3
正方形
第1课时
正方形的性质
人教版
八年级数学下册
教学课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
情景导学
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
你还能举出其他的例子吗?
情景导学
矩形
菱形
性质
1.四个角都____
1.四条边都是_______
2.对角线__________
2.对角线互相_________
且平分每组________
判定
1.有一个角是______的
___________
1.有一组邻边______的
__________
2.有三个角是_____的
_________
2.对角线互相______的
________
3.对角线________的
__________
3.四条边_______的
________
相等
直角
相等
相等
平行四边形
直角
对角
平分
相等
互相平分
平行四边形
相等
平行四边形
垂直
四边形
平行四边形
四边形
第二部分
新课目标
新课目标
1.理解正方形的概念.
2.探索并证明正方形的性质,并了解平行四边形、
矩形、菱形之间的联系和区别.(重点、难点)
3.会应用正方形的性质解决相关证明及计算问题.
(难点)
第三部分
新课进行时
新课进行时
核心知识点一
正方形的性质
矩
形
〃
〃
矩形怎样变化后就成了正方形呢?你有什么发现?
正方形
新课进行时
菱形怎样变化后就成了正方形呢?你有什么发现?
正方形
新课进行时
知识点一
正方形的定义
1、四条边_______,四个角都是_______的四边形叫做正方形.
2、正方形既是_____形,又是_____形.即
(1)有一组________相等的矩形是正方形.
(2)有一个角是________的菱形是正方形.
相等
直角
矩
菱
直角
邻边
新课进行时
已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.
A
B
C
D
证明:∵四边形ABCD是正方形.
∴∠A=90°,
AB=AC
(正方形的定义).
又∵正方形是平行四边形.
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
∴∠A=∠B
=∠C
=∠D
=
90°,
AB=
BC=CD=AD.
新课进行时
请同学们拿出准备好的正方形纸片,折一折,观察并思考.??正方形是不是轴对称图形?如果是,那么对称轴有几条?
对称性:
.
对称轴:
.
轴对称图形
4条
A
B
C
D
新课进行时
1、正方形具有_____的性质,同时又具有______的性质.
边:对边________,四边_________;
角:四个角都是________;
线:对角线相等,互相________,每条对角线平分一组________.
形:是_______________对称图形.
2、正方形与平行四边形、矩形、菱形之间的关系有怎样的包含关系?请填入下图中.
菱形
矩形
直角
都相等
相等
轴对称和中心
平分
对角
菱形
正方形
矩形
新课进行时
求证:
正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
A
D
C
B
O
已知:
如图,四边形ABCD是正方形,对角线AC、BD相
交于点O.
求证:
△ABO、
△BCO、
△CDO、
△DAO是全等
的等腰直角三角形.
证明:
∵
四边形ABCD是正方形,
∴
AC=BD,AC⊥BD,AO=BO=CO=DO.
∴
△ABO、
△BCO、
△CDO、
△DAO都
是等腰直角三角形,并且
△ABO≌
△BCO
≌
△CDO
≌
△DAO.
新课进行时
如图,在正方形ABCD中,
ΔBEC是等边三角形,
求证:
∠EAD=∠EDA=15°
.
证明:∵
ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵
四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD,
∠ABE=
∠DCE=30°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE=
∠BEA=
∠CDE=
∠CED=75°,
∴∠EAD=
∠EDA=90°-75°=15°.
新课进行时
当等边△ADE在正方形ABCD内部时,如图②,
AB=AE,∠BAE=90°-60°=30°,
∴∠AEB=75°.
同理可得∠DEC=75°.
∴∠BEC=360°-75°-75°-60°=150°.
综上所述,∠BEC的大小为30°或150°.
易错提醒:因为等边△ADE与正方形ABCD有一条公共边,所以边相等.本题分两种情况:等边△ADE在正方形的外部或在正方形的内部.
新课进行时
如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.
(1)求证:△APB≌△DPC;
解:∵四边形ABCD是正方形,
∴∠ABC=∠DCB=90°.
∵PB=PC,
∴∠PBC=∠PCB.
∴∠ABC-∠PBC=∠DCB-∠PCB,
即∠ABP=∠DCP.
又∵AB=DC,PB=PC,
∴△APB≌△DPC.
新课进行时
证明:∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°.
∵△APB≌△DPC,
∴AP=DP.
又∵AP=AB=AD,
∴DP=AP=AD.
∴△APD是等边三角形.
∴∠DAP=60°.
∴∠PAC=∠DAP-∠DAC=15°.
∴∠BAP=∠BAC-∠PAC=30°.
∴∠BAP=2∠PAC.
(2)求证:∠BAP=2∠PAC.
新课进行时
如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E,
PF⊥DC于F.试说明:AP=EF.
A
B
C
D
P
E
F
解:
连接PC,AC.
又∵PE⊥BC
,
PF⊥DC,
∵四边形ABCD是正方形,
∴∠FCE=90°,
AC垂直平分BD,
∴四边形PECF是矩形,
∴PC=EF.
∴AP=PC.
∴AP=EF.
在正方形的条件下证明两条线段相等:通常连接对角线构造垂直平分的模型,利用垂直平分线性质,角平分线性质,等腰三角形等来说明.
归纳
第四部分
知识小结
知识小结
1.四个角都是直角
2.四条边都相等
3.对角线相等且互相垂直平分
正方形的性质
性质
定义
有一组邻相等,并且有一个角是直角的平行四边形叫做正方形.
第五部分
随堂演练
随堂演练
满足下列条件的四边形是不是正方形?为什么?
(1)对角线互相垂直且相等的平行四边形;
(2)对角线互相垂直的矩形;
(3)对角线相等的菱形;
(4)对角线互相垂直平分且相等的四边形.
解:(1)根据正方形的性质可知,是正方形
(2)根据正方形的性质可知,是正方形
(3)根据正方形的性质可知,是正方形
(4)根据正方形的性质可知,是正方形
随堂演练
1.正方形具有而矩形不一定具有的性质是
(
)
A.四个角相等
B.对角线互相垂直平分
C.对角互补
D.对角线相等
2.正方形具有而菱形不一定具有的性质(
)
A.四条边相等
B.对角线互相垂直平分
C.对角线平分一组对角
D.对角线相等
B
D
随堂演练
3.如图,四边形ABCD是正方形,对角线AC与BD相交于点O,AO=2,求正方形的周长与面积.
解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OD=2.
在Rt△AOD中,由勾股定理,得
∴正方形的周长为4AD=
,
面积为AD2=8.
随堂演练
2.一个正方形的对角线长为2cm,则它的面积是
( )
A.2cm2
B.4cm2
C.6cm2
D.8cm2
A
1.平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
A
随堂演练
3.在正方形ABC中,∠ADB=
,∠DAC=
,
∠BOC=
.
4.在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是
.
A
D
B
C
O
A
D
B
C
O
E
45°
90°
22.5°
第3题图
第4题图
45°
5.如图,正方形ABCD的边长为1cm,AC为对角线,AE平分∠BAC,EF⊥AC,求BE的长.
解:∵四边形ABCD为正方形,
∴∠B=90°,∠ACB=45°,AB=BC=1cm.
∵EF⊥AC,∴∠EFA=∠EFC=90°.
又∵∠ECF=45°,
∴△EFC是等腰直角三角形,∴EF=FC.
∵∠BAE=∠FAE,∠B=∠EFA=90°,AE=AE,
∴△ABE≌△AFE,
∴AB=AF=1cm,BE=EF.
∴FC=BE.
在Rt△ABC中,
∴FC=AC-AF=(
-1)cm,
∴BE=(
-1)cm.
随堂演练
6.
如图在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF.
BE与DF之间有怎样的关系?请说明理由.
解:BE=DF,且BE⊥DF.理由如下:
∵四边形ABCD是正方形.
∴BC=DC,∠BCE
=90°
.
∴∠DCF=180°-∠BCE=90°.
∴∠BCE=∠DCF.
又∵CE=CF.
∴△BCE≌△DCF.
∴BE=DF.
A
B
D
C
F
E
随堂演练
延长BE交DE于点M,
∵△BCE≌△DCF
,
∴∠CBE
=∠CDF.
∵∠DCF
=90°
,
∴∠CDF
+∠F
=90°,
∴∠CBE+∠F=90°
,
∴∠BMF=90°.
∴BE⊥DF.
A
B
D
F
E
C
M
随堂演练
已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.
解:∵∠C=90°,DE⊥BC于E,
DF⊥AC于F
∴四边形CEDF有三个直角,
它是矩形
又∵CD平分∠ACB
根据角平分线上的点都两边的距离相等,可知DE=DF,所以矩形CEDF有一组邻边相等
根据正方形的判定方法,知四边形CEDF是正方形
随堂演练
1、根据图形所具有的性质,在下表相应的空格中打“√”
平行四边形
矩形
菱形
正方形
对边平行且相等
四边都相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
第六部分
课后作业
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
