第四章 单元检测题(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第四单元检测题
(时间:90分钟 满分:120分)
一、选择题(每小题4分,共48分)
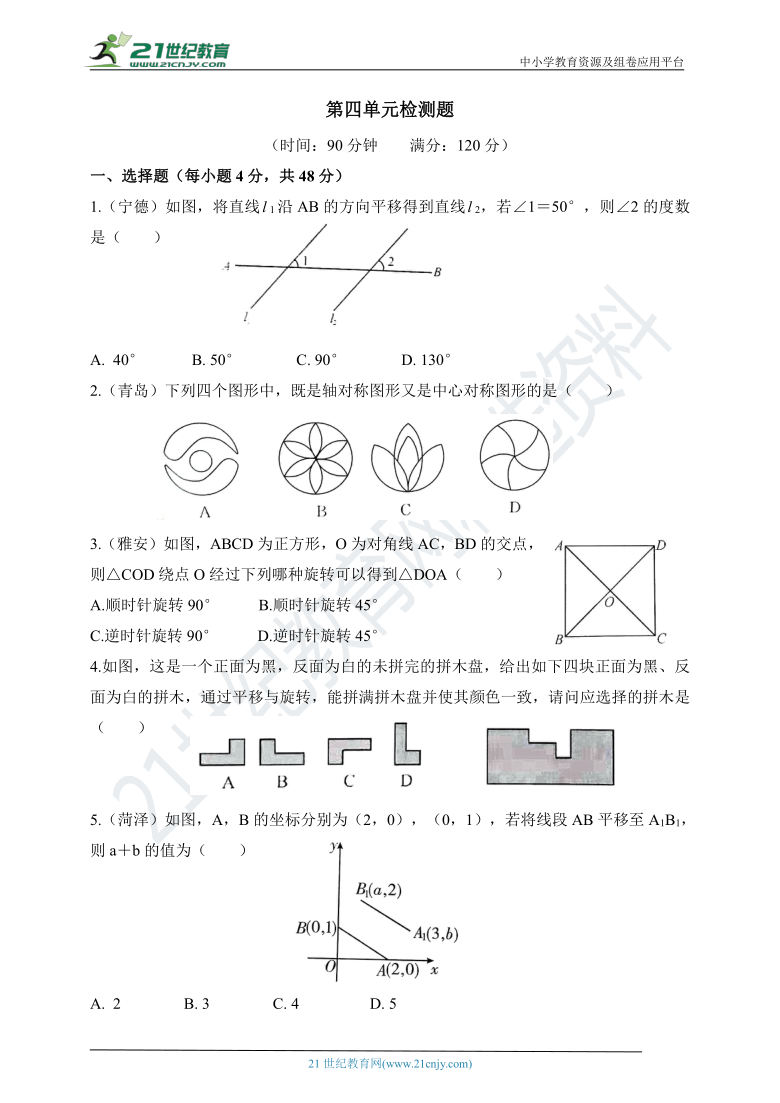
1.(宁德)如图,将直线1沿AB的方向平移得到直线2,若∠1=50°,则∠2的度数是( )
40° B. 50° C. 90° D. 130°
2.(青岛)下列四个图形中,既是轴对称图形又是中心对称图形的是( )
3.(雅安)如图,ABCD为正方形,O为对角线AC,BD的交点,则△COD绕点O经过下列哪种旋转可以得到△DOA( )
A.顺时针旋转90° B.顺时针旋转45°
C.逆时针旋转90° D.逆时针旋转45°
4.如图,这是一个正面为黑,反面为白的未拼完的拼木盘,给出如下四块正面为黑、反面为白的拼木,通过平移与旋转,能拼满拼木盘并使其颜色一致,请问应选择的拼木是( )
5.(菏泽)如图,A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
2 B. 3 C. 4 D. 5
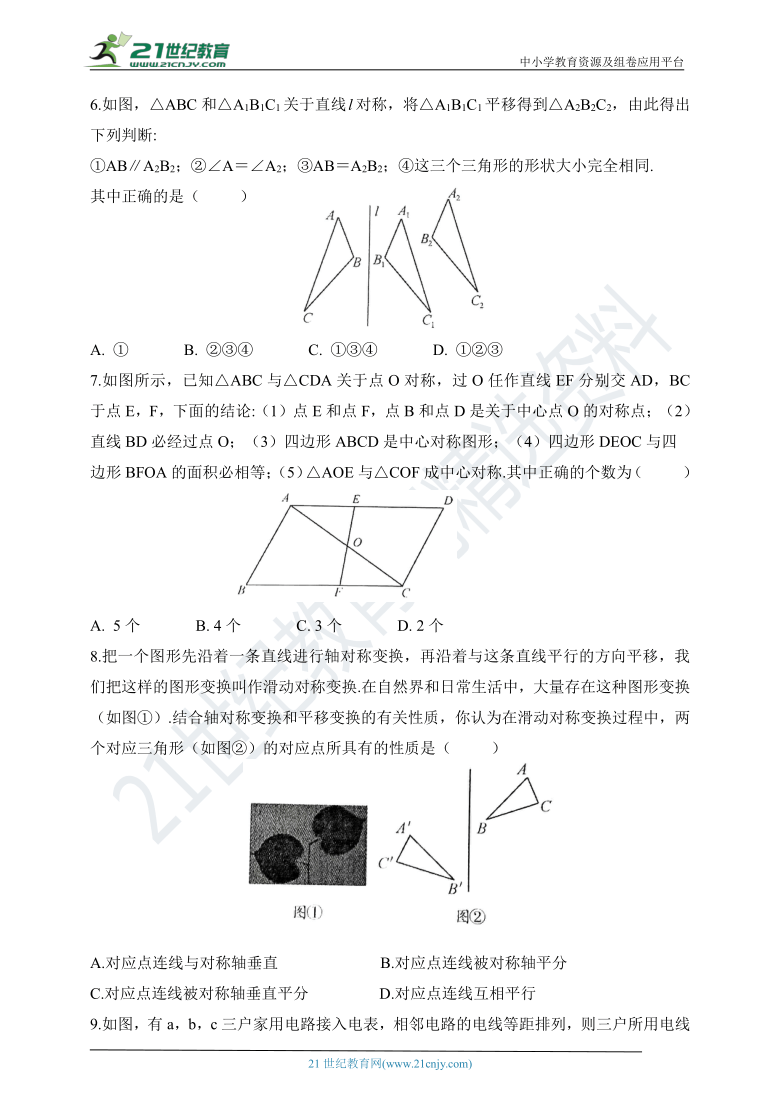
6.如图,△ABC和△A1B1C1关于直线对称,将△A1B1C1平移得到△A2B2C2,由此得出下列判断:
①AB∥A2B2;②∠A=∠A2;③AB=A2B2;④这三个三角形的形状大小完全相同.
其中正确的是( )
① B. ②③④ C. ①③④ D. ①②③
7.如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD,BC于点E,F,下面的结论:(1)点E和点F,点B和点D是关于中心点O的对称点;(2)直线BD必经过点O;(3)四边形ABCD是中心对称图形;(4)四边形DEOC与四
边形BFOA的面积必相等;(5)△AOE与△COF成中心对称.其中正确的个数为( )
5个 B. 4个 C. 3个 D. 2个
8.把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫作滑动对称变换.在自然界和日常生活中,大量存在这种图形变换(如图①).结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图②)的对应点所具有的性质是( )
A.对应点连线与对称轴垂直 B.对应点连线被对称轴平分
C.对应点连线被对称轴垂直平分 D.对应点连线互相平行
9.如图,有a,b,c三户家用电路接入电表,相邻电路的电线等距排列,则三户所用电线( )
a户最长 B. b户最长 C. c户最长 D. 三户一样长
10.把一幅三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长为( )
3 B. 5 C. 4 D.
11.(丽水)如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有( )
3种 B. 6种 C. 8种 D. 12种
12.(济南)在平面直角坐标系中有三个点A(1,-1),B(-1,-1),C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点为P2,P2关于C的对称点为P3,按此规律继续以A,B,C为对称中心重复前面的操作,依次得到P4,P5,P6……则点P2015的坐标是( )
A.(0,0) B.(0,2) C.(2,-4) D.(-4,2)
二、填空题(每小题4分,共20分)
13.请写出一个既是轴对称图形,又是中心对称图形的汉字____________。
14.如图,把“QQ”笑脸放在直角坐标系中,已知眼睛A的坐标是(-2,3),嘴唇C的坐标为(-1,1),则将此“QQ”笑脸向右平移3个单位后,眼睛B的坐标是_________。
15.如图,将正方形CFED旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有__________个。
16.如图,△ABC中,∠B=70°,∠BAC=30°,将△ABC绕点C顺时针旋转得△EDC.当点B的对应点D恰好落在AC上时,∠CAE=___________。
17.如图是一组密码的一部分.为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“今天考试”的真实意思是“努力发挥”.若“今”所处的位置为(x,y),你找到的密码钥匙是(___________________),破译“正做数学”的真实意思是“_____________________”。
三、解答题(共52分)
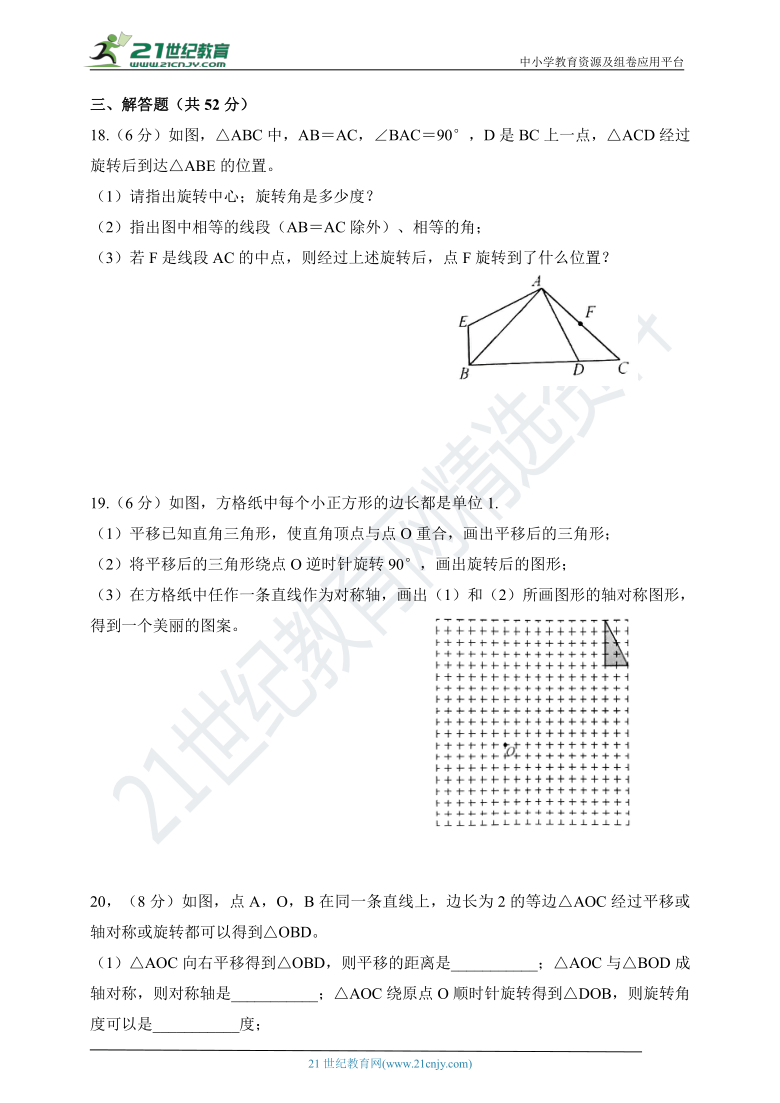
18.(6分)如图,△ABC中,AB=AC,∠BAC=90°,D是BC上一点,△ACD经过旋转后到达△ABE的位置。
(1)请指出旋转中心;旋转角是多少度?
(2)指出图中相等的线段(AB=AC除外)、相等的角;
(3)若F是线段AC的中点,则经过上述旋转后,点F旋转到了什么位置?
19.(6分)如图,方格纸中每个小正方形的边长都是单位1.
(1)平移已知直角三角形,使直角顶点与点O重合,画出平移后的三角形;
(2)将平移后的三角形绕点O逆时针旋转90°,画出旋转后的图形;
(3)在方格纸中任作一条直线作为对称轴,画出(1)和(2)所画图形的轴对称图形,得到一个美丽的图案。
20,(8分)如图,点A,O,B在同一条直线上,边长为2的等边△AOC经过平移或轴对称或旋转都可以得到△OBD。
(1)△AOC向右平移得到△OBD,则平移的距离是___________;△AOC与△BOD成轴对称,则对称轴是___________;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是___________度;
(2)连接AD,交OC于点E,请利用轴对称的知识,求∠AEO的度数.
21.(8分)如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2)B(0,5),C(0,2)。
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形;
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形;
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2请直接写出旋转中心的坐标。
22.(8分)如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°后至△DBE,再把△ABC沿射线AB平移至△FEG,DE,FG相交于点H.试判断DE,FG的位置关系,并说明理由。
23.(8分)如图,在一块水平长为a、纵向宽为b的矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位长度),请你猜想空白部分表示的草地面积是多少?并说明你的猜想是正确的.
24.(8分)探索下列问题:
(1)在图1给出的四个正方形中,各画出一条直线(依次是:水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线),将每个正方形都分割成面积相等的两部分;
(2)一条竖直方向的直线m以及任意的直线n,在由左向右平移的过程中,将正六边形分成左右两部分,其面积分别记为S1和S2。
①请你在图2中相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”“=”或“>”连接);
②请你在图3中分别画出反映S1与S2三种大小关系的直线n,并在相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”“=”或“>”连接)。
(3)是否存在一条直线,将一个任意的平面图形(如图4)分割成面积相等的两部分,请简略说出理由.
参考答案
B 2. B 3. C 4. B 5. A 6. B 7. A
B 9. D 10. B 11. B 12. A
答案不唯一,如:一、中、田等 14. (3,3) 15. 3 16. 50?
x+1,y+2
18,解: (1)点A是旋转中心;旋转角是90?.
(2) AE=AD, BE=CD,∠BAE=∠CAD, ∠E=∠ADC, ∠ABE=∠C,∠BAC=∠EAD, ∠ABC=∠ACB.
(3)点F旋转到了线段AB的中点位置.
19,解:如图所示.
(1)把右上角的已知直角三角形向下平移7个单位,然后再向左平移9个单位,即到达指定位置.
(2)利用旋转作图,或借助网格画图,易于得到旋转后的直角三角形.
(3)以经过点O的水平线为对称轴,画轴对称图形,即得到一个“鱼形”美丽图案.
20.解:(1)2 直线m 120
(2)由题意,得 ∠AOC=∠DOC,OA=OD,故线段OA沿直线OC折叠,能与线段OD重合,即线段OA与段OD关于直线0C成轴对称,且点A与点D是对称点,所以线段AD被对称轴OC垂直平分,所以∠AEO=90°。
21,解:(1) (2)画图如图所示:
(3)旋转中心为直线B1B2,和A1A2的交点,由上图可知旋转中心坐标为(0, —2).
22.解:DE⊥FG,理由如下:∵△DBE与△FEG是由△ABC分别经过旋转与平移得到的,∴ ∠A=∠EDB=∠GFE, ∠ABC=∠DBE=90?,∴∠BDE+∠BED=90?。
∴∠GFE+∠BED=90?.∴∠FHE =90,即DE⊥ FG.
23,解:可以猜想草地面积为ab-b.方法是先把“小路”沿着左右两个边界“剪去”,再将左侧的草地向右平移一个单位,得到一个新的矩形(如图所示),理由是,在新得到的矩形中,其纵向宽仍为b,而水平长则变成了a-1,所以草地的面积就是b(a-1)
=ab-b.
24,解:(1)如图.
(2)①S1<S2;S1=S2 ;S1>S2.
②如图.
(3)存在,对于任意一条直线,在直线从平面图形的一侧向另一侧平移的过程中,当图形被直线分割后,设直线两侧图形的面积分别为S1、S2.两侧图形的面积由S1<S2(或S1>S2)的情形逐渐变为S1>S2(或S1<S2 )的情形,在这个平移过程中,一定会存在S1=S2的时刻.因此,一定存在一条直线,将一个任意平面图形分割成面积相等的两部分.
_21?????????è?????(www.21cnjy.com)_
第四单元检测题
(时间:90分钟 满分:120分)
一、选择题(每小题4分,共48分)
1.(宁德)如图,将直线1沿AB的方向平移得到直线2,若∠1=50°,则∠2的度数是( )
40° B. 50° C. 90° D. 130°
2.(青岛)下列四个图形中,既是轴对称图形又是中心对称图形的是( )
3.(雅安)如图,ABCD为正方形,O为对角线AC,BD的交点,则△COD绕点O经过下列哪种旋转可以得到△DOA( )
A.顺时针旋转90° B.顺时针旋转45°
C.逆时针旋转90° D.逆时针旋转45°
4.如图,这是一个正面为黑,反面为白的未拼完的拼木盘,给出如下四块正面为黑、反面为白的拼木,通过平移与旋转,能拼满拼木盘并使其颜色一致,请问应选择的拼木是( )
5.(菏泽)如图,A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
2 B. 3 C. 4 D. 5
6.如图,△ABC和△A1B1C1关于直线对称,将△A1B1C1平移得到△A2B2C2,由此得出下列判断:
①AB∥A2B2;②∠A=∠A2;③AB=A2B2;④这三个三角形的形状大小完全相同.
其中正确的是( )
① B. ②③④ C. ①③④ D. ①②③
7.如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD,BC于点E,F,下面的结论:(1)点E和点F,点B和点D是关于中心点O的对称点;(2)直线BD必经过点O;(3)四边形ABCD是中心对称图形;(4)四边形DEOC与四
边形BFOA的面积必相等;(5)△AOE与△COF成中心对称.其中正确的个数为( )
5个 B. 4个 C. 3个 D. 2个
8.把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫作滑动对称变换.在自然界和日常生活中,大量存在这种图形变换(如图①).结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图②)的对应点所具有的性质是( )
A.对应点连线与对称轴垂直 B.对应点连线被对称轴平分
C.对应点连线被对称轴垂直平分 D.对应点连线互相平行
9.如图,有a,b,c三户家用电路接入电表,相邻电路的电线等距排列,则三户所用电线( )
a户最长 B. b户最长 C. c户最长 D. 三户一样长
10.把一幅三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长为( )
3 B. 5 C. 4 D.
11.(丽水)如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有( )
3种 B. 6种 C. 8种 D. 12种
12.(济南)在平面直角坐标系中有三个点A(1,-1),B(-1,-1),C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点为P2,P2关于C的对称点为P3,按此规律继续以A,B,C为对称中心重复前面的操作,依次得到P4,P5,P6……则点P2015的坐标是( )
A.(0,0) B.(0,2) C.(2,-4) D.(-4,2)
二、填空题(每小题4分,共20分)
13.请写出一个既是轴对称图形,又是中心对称图形的汉字____________。
14.如图,把“QQ”笑脸放在直角坐标系中,已知眼睛A的坐标是(-2,3),嘴唇C的坐标为(-1,1),则将此“QQ”笑脸向右平移3个单位后,眼睛B的坐标是_________。
15.如图,将正方形CFED旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有__________个。
16.如图,△ABC中,∠B=70°,∠BAC=30°,将△ABC绕点C顺时针旋转得△EDC.当点B的对应点D恰好落在AC上时,∠CAE=___________。
17.如图是一组密码的一部分.为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“今天考试”的真实意思是“努力发挥”.若“今”所处的位置为(x,y),你找到的密码钥匙是(___________________),破译“正做数学”的真实意思是“_____________________”。
三、解答题(共52分)
18.(6分)如图,△ABC中,AB=AC,∠BAC=90°,D是BC上一点,△ACD经过旋转后到达△ABE的位置。
(1)请指出旋转中心;旋转角是多少度?
(2)指出图中相等的线段(AB=AC除外)、相等的角;
(3)若F是线段AC的中点,则经过上述旋转后,点F旋转到了什么位置?
19.(6分)如图,方格纸中每个小正方形的边长都是单位1.
(1)平移已知直角三角形,使直角顶点与点O重合,画出平移后的三角形;
(2)将平移后的三角形绕点O逆时针旋转90°,画出旋转后的图形;
(3)在方格纸中任作一条直线作为对称轴,画出(1)和(2)所画图形的轴对称图形,得到一个美丽的图案。
20,(8分)如图,点A,O,B在同一条直线上,边长为2的等边△AOC经过平移或轴对称或旋转都可以得到△OBD。
(1)△AOC向右平移得到△OBD,则平移的距离是___________;△AOC与△BOD成轴对称,则对称轴是___________;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是___________度;
(2)连接AD,交OC于点E,请利用轴对称的知识,求∠AEO的度数.
21.(8分)如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2)B(0,5),C(0,2)。
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形;
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形;
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2请直接写出旋转中心的坐标。
22.(8分)如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°后至△DBE,再把△ABC沿射线AB平移至△FEG,DE,FG相交于点H.试判断DE,FG的位置关系,并说明理由。
23.(8分)如图,在一块水平长为a、纵向宽为b的矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位长度),请你猜想空白部分表示的草地面积是多少?并说明你的猜想是正确的.
24.(8分)探索下列问题:
(1)在图1给出的四个正方形中,各画出一条直线(依次是:水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线),将每个正方形都分割成面积相等的两部分;
(2)一条竖直方向的直线m以及任意的直线n,在由左向右平移的过程中,将正六边形分成左右两部分,其面积分别记为S1和S2。
①请你在图2中相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”“=”或“>”连接);
②请你在图3中分别画出反映S1与S2三种大小关系的直线n,并在相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”“=”或“>”连接)。
(3)是否存在一条直线,将一个任意的平面图形(如图4)分割成面积相等的两部分,请简略说出理由.
参考答案
B 2. B 3. C 4. B 5. A 6. B 7. A
B 9. D 10. B 11. B 12. A
答案不唯一,如:一、中、田等 14. (3,3) 15. 3 16. 50?
x+1,y+2
18,解: (1)点A是旋转中心;旋转角是90?.
(2) AE=AD, BE=CD,∠BAE=∠CAD, ∠E=∠ADC, ∠ABE=∠C,∠BAC=∠EAD, ∠ABC=∠ACB.
(3)点F旋转到了线段AB的中点位置.
19,解:如图所示.
(1)把右上角的已知直角三角形向下平移7个单位,然后再向左平移9个单位,即到达指定位置.
(2)利用旋转作图,或借助网格画图,易于得到旋转后的直角三角形.
(3)以经过点O的水平线为对称轴,画轴对称图形,即得到一个“鱼形”美丽图案.
20.解:(1)2 直线m 120
(2)由题意,得 ∠AOC=∠DOC,OA=OD,故线段OA沿直线OC折叠,能与线段OD重合,即线段OA与段OD关于直线0C成轴对称,且点A与点D是对称点,所以线段AD被对称轴OC垂直平分,所以∠AEO=90°。
21,解:(1) (2)画图如图所示:
(3)旋转中心为直线B1B2,和A1A2的交点,由上图可知旋转中心坐标为(0, —2).
22.解:DE⊥FG,理由如下:∵△DBE与△FEG是由△ABC分别经过旋转与平移得到的,∴ ∠A=∠EDB=∠GFE, ∠ABC=∠DBE=90?,∴∠BDE+∠BED=90?。
∴∠GFE+∠BED=90?.∴∠FHE =90,即DE⊥ FG.
23,解:可以猜想草地面积为ab-b.方法是先把“小路”沿着左右两个边界“剪去”,再将左侧的草地向右平移一个单位,得到一个新的矩形(如图所示),理由是,在新得到的矩形中,其纵向宽仍为b,而水平长则变成了a-1,所以草地的面积就是b(a-1)
=ab-b.
24,解:(1)如图.
(2)①S1<S2;S1=S2 ;S1>S2.
②如图.
(3)存在,对于任意一条直线,在直线从平面图形的一侧向另一侧平移的过程中,当图形被直线分割后,设直线两侧图形的面积分别为S1、S2.两侧图形的面积由S1<S2(或S1>S2)的情形逐渐变为S1>S2(或S1<S2 )的情形,在这个平移过程中,一定会存在S1=S2的时刻.因此,一定存在一条直线,将一个任意平面图形分割成面积相等的两部分.
_21?????????è?????(www.21cnjy.com)_
