北师大版九年级数学下册 4.2 圆周角定理的推论(Word版 含答案)
文档属性
| 名称 | 北师大版九年级数学下册 4.2 圆周角定理的推论(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 480.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 00:00:00 | ||
图片预览



文档简介
北师大版九年级数学下第三章4
圆周角和圆心角的关系4.2
圆周角定理的推论(含答案)
一、选择题
1.下列命题中,正确的有( )
①90°的圆周角所对的弦是直径;
②若圆周角相等,则它们所对的弧也相等;
③同圆中,相等的圆周角所对的弦也相等.
A.0个
B.1个
C.2个
D.3个
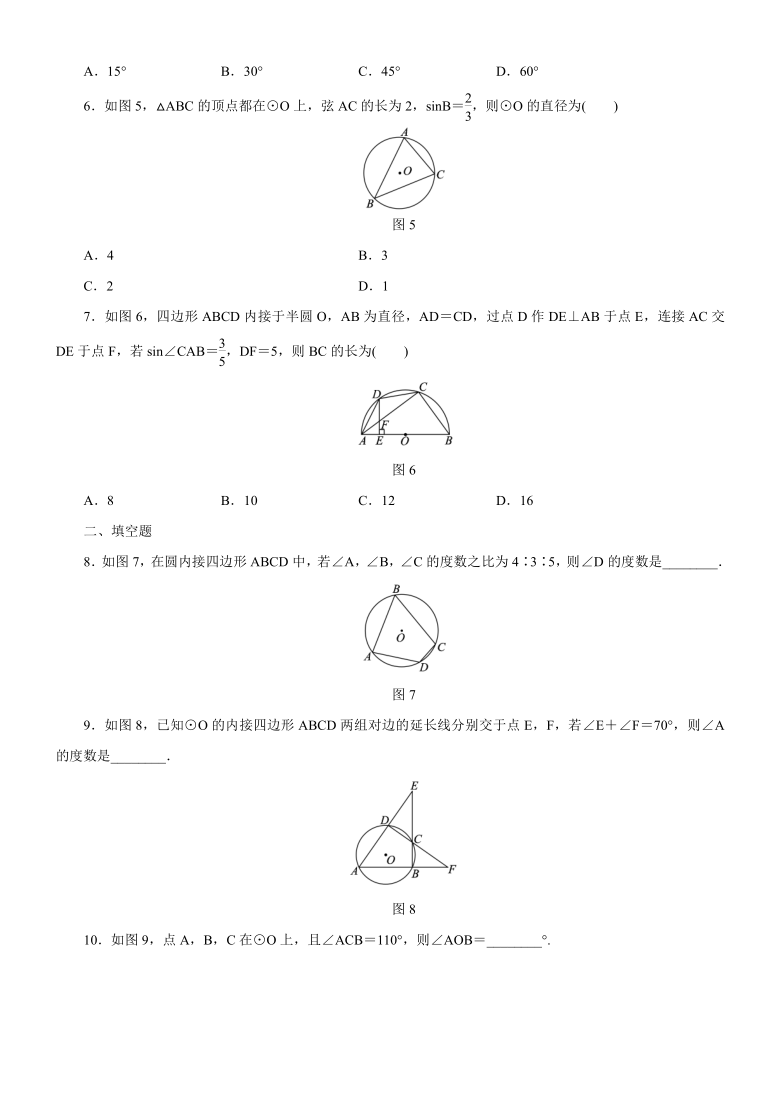
2.从下列三角尺与圆弧的位置关系中,可判断圆弧为半圆的是( )
图1
3.如图2,AB为⊙O的直径,C,D为⊙O上两点,若∠BCD=40°,则∠ABD的度数为( )
图2
A.60°
B.50°
C.40°
D.20°
4.如图3,CD是⊙O的直径,若∠1=30°,则∠2的度数为( )
图3
A.30°
B.45°
C.60°
D.70°
5.如图4,⊙A过点O(0,0),C(,0),且⊙A的半径是1,B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是( )
图4
A.15°
B.30°
C.45°
D.60°
6.如图5,△ABC的顶点都在⊙O上,弦AC的长为2,sinB=,则⊙O的直径为( )
图5
A.4
B.3
C.2
D.1
7.如图6,四边形ABCD内接于半圆O,AB为直径,AD=CD,过点D作DE⊥AB于点E,连接AC交DE于点F,若sin∠CAB=,DF=5,则BC的长为( )
图6
A.8
B.10
C.12
D.16
二、填空题
8.如图7,在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4∶3∶5,则∠D的度数是________.
图7
9.如图8,已知⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F,若∠E+∠F=70°,则∠A的度数是________.
图8
10.如图9,点A,B,C在⊙O上,且∠ACB=110°,则∠AOB=________°.
图9
11.如图10,已知在半圆O中,AB是直径,AD=DC,∠CAB=30°,AC=2
,则AD的长为________.
图10
三、解答题
12.已知在⊙O的内接四边形ABCD中,AD=BC,AD∥BC.试判断四边形ABCD的形状,并加以证明.
13.如图11,四边形ABCD内接于⊙O,∠B=50°,∠ACD=25°,∠BAD=65°.求证:
(1)AD=CD;
(2)AB是⊙O的直径.
图11
14.如图12,△ABC内接于⊙O且AB=AC,延长BC至点D,使CD=AC,连接AD交⊙O于点E,连接BE,CE.
(1)求证:△ABE≌△CDE.
(2)填空:
①连接AO,CO,当∠ABC的度数为________时,四边形AOCE是菱形;
②若AE=6,EF=4,则DE的长为________.
图12
附加题
图形变换题已知:如图13,AB是⊙O的一条弦,C为的中点,CD是⊙O的直径,过点C的直线l交AB所在直线于点E,交⊙O于点F,连接DF.
(1)猜想∠CEB与∠FDC的数量关系,并证明你的结论;
(2)将直线l绕点C旋转(与CD不重合),在旋转过程中,点E,F的位置也随之变化,请在下面的两个备用图中分别画出直线l在不同位置时,使(1)中的结论仍然成立的图形,标上相应字母,并选其中一个图形给予证明.
图13
参考答案
1.[答案]
C
2.[答案]
B
3.[解析]
B ∵AB为⊙O的直径,∴∠ADB=90°.∵∠A和∠BCD都是弧BD所对的圆周角,∴∠A=∠BCD=40°,∴∠ABD=90°-40°=50°.故选B.
4.[解析]
C 如图,连接AD.
∵CD是⊙O的直径,
∴∠CAD=90°(直径所对的圆周角是直角).
又∵∠1=30°,
∴∠DAB=60°.
∵∠DAB=∠2(同弧所对的圆周角相等),
∴∠2=60°.故选C.
5.[答案]
B
6.[解析]
B 作直径AD,连接CD,则∠ACD=90°.∵∠D=∠B,∴sinD=sinB=.
在Rt△ADC中,∵AC=2,∴AD==3,
∴⊙O的直径为3.
故选B.
7.[解析]
C 连接BD.∵AD=CD,
∴∠DAC=∠ACD.
∵AB为直径,∴∠ADB=∠ACB=90°,
∴∠DAB+∠ABD=90°.
∵DE⊥AB,∴∠DAB+∠ADE=90°,
∴∠ADE=∠ABD.
∵∠ABD=∠ACD,∴∠DAC=∠ADE,
∴AF=DF=5.
在Rt△AEF中,sin∠CAB==,
∴EF=3,∴AE=4,DE=3+5=8.
易得△ADE∽△DBE,∴=,
∴BE===16,
∴AB=16+4=20.
在Rt△ABC中,sin∠CAB==,
∴BC=12.
8.[答案]
120°
[解析]
∵∠A,∠B,∠C的度数之比为4∶3∶5,∴设∠A=4x,则∠B=3x,∠C=5x.
∵四边形ABCD是圆内接四边形,∴∠A+∠C=180°,即4x+5x=180°,解得x=20°,
∴∠B=3x=60°,∴∠D=180°-60°=120°.
9.[答案]
55°
[解析]
∵四边形ABCD为⊙O的内接四边形,∴∠A+∠BCD=∠BCF+∠BCD=180°,
∴∠A=∠BCF.
∵∠EBF=∠A+∠E,而∠EBF=180°-∠BCF-∠F,
∴∠A+∠E=180°-∠BCF-∠F,
∴∠A+∠E=180-∠A-∠F,
即2∠A=180°-(∠E+∠F)=110°,
∴∠A=55°.
10.[答案]
140
[解析]
作劣弧AB所对的圆周角∠ADB,如图,则∠ACB+∠ADB=180°,
∴∠ADB=180°-110°=70°,
∴∠AOB=2∠ADB=140°.
11.[答案]
2
[解析]
∵AB是半圆O的直径,
∴∠ACB=90°.
∵∠CAB=30°,∴∠ABC=60°.
∵AD=DC,且所对的圆心角为30°×2=60°,
∴,,所对的圆心角均为60°,
∴BC=AD.
在Rt△ABC中,∵∠CAB=30°,AC=2
,
∴BC=2
×tan30°=2,
∴AD=2.
12.[解析]
因为AD=BC,AD∥BC,所以四边形ABCD是平行四边形.再根据圆内接四边形的性质可得出∠B=∠D=90°,因此,四边形ABCD是矩形.
解:四边形ABCD为矩形.
证明:如图.
∵AD∥BC,AD=BC,
∴四边形ABCD为平行四边形,
∴∠B=∠D.
∵四边形ABCD内接于⊙O,
∴∠B+∠D=180°,
∴∠B=∠D=90°,
∴?ABCD是矩形.
13.证明:(1)∵四边形ABCD内接于⊙O,
∴∠D=180°-∠B=130°.
∵∠ACD=25°,
∴∠DAC=180°-∠D-∠ACD=25°,
∴∠DAC=∠ACD,
∴AD=CD.
(2)∵∠BAC=∠BAD-∠DAC=65°-25°=40°,∠B=50°,
∴∠ACB=180°-∠B-∠BAC=90°,
∴AB是⊙O的直径.
14.解:(1)证明:∵AB=AC,CD=AC,
∴∠ABC=∠ACB,AB=CD.
∵四边形ABCE是圆内接四边形,
∴∠ECD=∠EAB,∠CED=∠ABC.
∵∠ABC=∠ACB=∠AEB,
∴∠CED=∠AEB.
在△ABE和△CDE中,
∵∠AEB=∠CED,∠EAB=∠ECD,AB=CD,
∴△ABE≌△CDE(AAS).
(2)①60° ②9
附加题
[解析]
(1)根据垂径定理的推论得到CD⊥AB,根据圆周角定理的推论得到∠CFD=90°,然后通过等量代换证得∠CEB=∠FDC;(2)根据垂径定理得到CD⊥AB,∠CFD=90°,然后通过等量代换证得∠CEB=∠FDC.
解:(1)∠CEB=∠FDC.
证明:∵CD是⊙O的直径,C为的中点,
∴CD⊥AB,
∴∠CEB+∠ECD=90°.
∵CD是⊙O的直径,
∴∠CFD=90°,
∴∠FDC+∠ECD=90°,
∴∠CEB=∠FDC.
(2)所画图形与证明均不唯一,如图①②.
选图②进行证明:如图②.
∵CD是⊙O的直径,C为的中点,
∴CD⊥AB,∴∠CEB+∠ECD=90°.
∵CD是⊙O的直径,∴∠CFD=90°,
∴∠FDC+∠ECD=90°,∴∠CEB=∠FDC.
圆周角和圆心角的关系4.2
圆周角定理的推论(含答案)
一、选择题
1.下列命题中,正确的有( )
①90°的圆周角所对的弦是直径;
②若圆周角相等,则它们所对的弧也相等;
③同圆中,相等的圆周角所对的弦也相等.
A.0个
B.1个
C.2个
D.3个
2.从下列三角尺与圆弧的位置关系中,可判断圆弧为半圆的是( )
图1
3.如图2,AB为⊙O的直径,C,D为⊙O上两点,若∠BCD=40°,则∠ABD的度数为( )
图2
A.60°
B.50°
C.40°
D.20°
4.如图3,CD是⊙O的直径,若∠1=30°,则∠2的度数为( )
图3
A.30°
B.45°
C.60°
D.70°
5.如图4,⊙A过点O(0,0),C(,0),且⊙A的半径是1,B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是( )
图4
A.15°
B.30°
C.45°
D.60°
6.如图5,△ABC的顶点都在⊙O上,弦AC的长为2,sinB=,则⊙O的直径为( )
图5
A.4
B.3
C.2
D.1
7.如图6,四边形ABCD内接于半圆O,AB为直径,AD=CD,过点D作DE⊥AB于点E,连接AC交DE于点F,若sin∠CAB=,DF=5,则BC的长为( )
图6
A.8
B.10
C.12
D.16
二、填空题
8.如图7,在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4∶3∶5,则∠D的度数是________.
图7
9.如图8,已知⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F,若∠E+∠F=70°,则∠A的度数是________.
图8
10.如图9,点A,B,C在⊙O上,且∠ACB=110°,则∠AOB=________°.
图9
11.如图10,已知在半圆O中,AB是直径,AD=DC,∠CAB=30°,AC=2
,则AD的长为________.
图10
三、解答题
12.已知在⊙O的内接四边形ABCD中,AD=BC,AD∥BC.试判断四边形ABCD的形状,并加以证明.
13.如图11,四边形ABCD内接于⊙O,∠B=50°,∠ACD=25°,∠BAD=65°.求证:
(1)AD=CD;
(2)AB是⊙O的直径.
图11
14.如图12,△ABC内接于⊙O且AB=AC,延长BC至点D,使CD=AC,连接AD交⊙O于点E,连接BE,CE.
(1)求证:△ABE≌△CDE.
(2)填空:
①连接AO,CO,当∠ABC的度数为________时,四边形AOCE是菱形;
②若AE=6,EF=4,则DE的长为________.
图12
附加题
图形变换题已知:如图13,AB是⊙O的一条弦,C为的中点,CD是⊙O的直径,过点C的直线l交AB所在直线于点E,交⊙O于点F,连接DF.
(1)猜想∠CEB与∠FDC的数量关系,并证明你的结论;
(2)将直线l绕点C旋转(与CD不重合),在旋转过程中,点E,F的位置也随之变化,请在下面的两个备用图中分别画出直线l在不同位置时,使(1)中的结论仍然成立的图形,标上相应字母,并选其中一个图形给予证明.
图13
参考答案
1.[答案]
C
2.[答案]
B
3.[解析]
B ∵AB为⊙O的直径,∴∠ADB=90°.∵∠A和∠BCD都是弧BD所对的圆周角,∴∠A=∠BCD=40°,∴∠ABD=90°-40°=50°.故选B.
4.[解析]
C 如图,连接AD.
∵CD是⊙O的直径,
∴∠CAD=90°(直径所对的圆周角是直角).
又∵∠1=30°,
∴∠DAB=60°.
∵∠DAB=∠2(同弧所对的圆周角相等),
∴∠2=60°.故选C.
5.[答案]
B
6.[解析]
B 作直径AD,连接CD,则∠ACD=90°.∵∠D=∠B,∴sinD=sinB=.
在Rt△ADC中,∵AC=2,∴AD==3,
∴⊙O的直径为3.
故选B.
7.[解析]
C 连接BD.∵AD=CD,
∴∠DAC=∠ACD.
∵AB为直径,∴∠ADB=∠ACB=90°,
∴∠DAB+∠ABD=90°.
∵DE⊥AB,∴∠DAB+∠ADE=90°,
∴∠ADE=∠ABD.
∵∠ABD=∠ACD,∴∠DAC=∠ADE,
∴AF=DF=5.
在Rt△AEF中,sin∠CAB==,
∴EF=3,∴AE=4,DE=3+5=8.
易得△ADE∽△DBE,∴=,
∴BE===16,
∴AB=16+4=20.
在Rt△ABC中,sin∠CAB==,
∴BC=12.
8.[答案]
120°
[解析]
∵∠A,∠B,∠C的度数之比为4∶3∶5,∴设∠A=4x,则∠B=3x,∠C=5x.
∵四边形ABCD是圆内接四边形,∴∠A+∠C=180°,即4x+5x=180°,解得x=20°,
∴∠B=3x=60°,∴∠D=180°-60°=120°.
9.[答案]
55°
[解析]
∵四边形ABCD为⊙O的内接四边形,∴∠A+∠BCD=∠BCF+∠BCD=180°,
∴∠A=∠BCF.
∵∠EBF=∠A+∠E,而∠EBF=180°-∠BCF-∠F,
∴∠A+∠E=180°-∠BCF-∠F,
∴∠A+∠E=180-∠A-∠F,
即2∠A=180°-(∠E+∠F)=110°,
∴∠A=55°.
10.[答案]
140
[解析]
作劣弧AB所对的圆周角∠ADB,如图,则∠ACB+∠ADB=180°,
∴∠ADB=180°-110°=70°,
∴∠AOB=2∠ADB=140°.
11.[答案]
2
[解析]
∵AB是半圆O的直径,
∴∠ACB=90°.
∵∠CAB=30°,∴∠ABC=60°.
∵AD=DC,且所对的圆心角为30°×2=60°,
∴,,所对的圆心角均为60°,
∴BC=AD.
在Rt△ABC中,∵∠CAB=30°,AC=2
,
∴BC=2
×tan30°=2,
∴AD=2.
12.[解析]
因为AD=BC,AD∥BC,所以四边形ABCD是平行四边形.再根据圆内接四边形的性质可得出∠B=∠D=90°,因此,四边形ABCD是矩形.
解:四边形ABCD为矩形.
证明:如图.
∵AD∥BC,AD=BC,
∴四边形ABCD为平行四边形,
∴∠B=∠D.
∵四边形ABCD内接于⊙O,
∴∠B+∠D=180°,
∴∠B=∠D=90°,
∴?ABCD是矩形.
13.证明:(1)∵四边形ABCD内接于⊙O,
∴∠D=180°-∠B=130°.
∵∠ACD=25°,
∴∠DAC=180°-∠D-∠ACD=25°,
∴∠DAC=∠ACD,
∴AD=CD.
(2)∵∠BAC=∠BAD-∠DAC=65°-25°=40°,∠B=50°,
∴∠ACB=180°-∠B-∠BAC=90°,
∴AB是⊙O的直径.
14.解:(1)证明:∵AB=AC,CD=AC,
∴∠ABC=∠ACB,AB=CD.
∵四边形ABCE是圆内接四边形,
∴∠ECD=∠EAB,∠CED=∠ABC.
∵∠ABC=∠ACB=∠AEB,
∴∠CED=∠AEB.
在△ABE和△CDE中,
∵∠AEB=∠CED,∠EAB=∠ECD,AB=CD,
∴△ABE≌△CDE(AAS).
(2)①60° ②9
附加题
[解析]
(1)根据垂径定理的推论得到CD⊥AB,根据圆周角定理的推论得到∠CFD=90°,然后通过等量代换证得∠CEB=∠FDC;(2)根据垂径定理得到CD⊥AB,∠CFD=90°,然后通过等量代换证得∠CEB=∠FDC.
解:(1)∠CEB=∠FDC.
证明:∵CD是⊙O的直径,C为的中点,
∴CD⊥AB,
∴∠CEB+∠ECD=90°.
∵CD是⊙O的直径,
∴∠CFD=90°,
∴∠FDC+∠ECD=90°,
∴∠CEB=∠FDC.
(2)所画图形与证明均不唯一,如图①②.
选图②进行证明:如图②.
∵CD是⊙O的直径,C为的中点,
∴CD⊥AB,∴∠CEB+∠ECD=90°.
∵CD是⊙O的直径,∴∠CFD=90°,
∴∠FDC+∠ECD=90°,∴∠CEB=∠FDC.
