北师大版九年级数学下册 3.9 弧长及扇形的面积(Word版 含答案)
文档属性
| 名称 | 北师大版九年级数学下册 3.9 弧长及扇形的面积(Word版 含答案) | 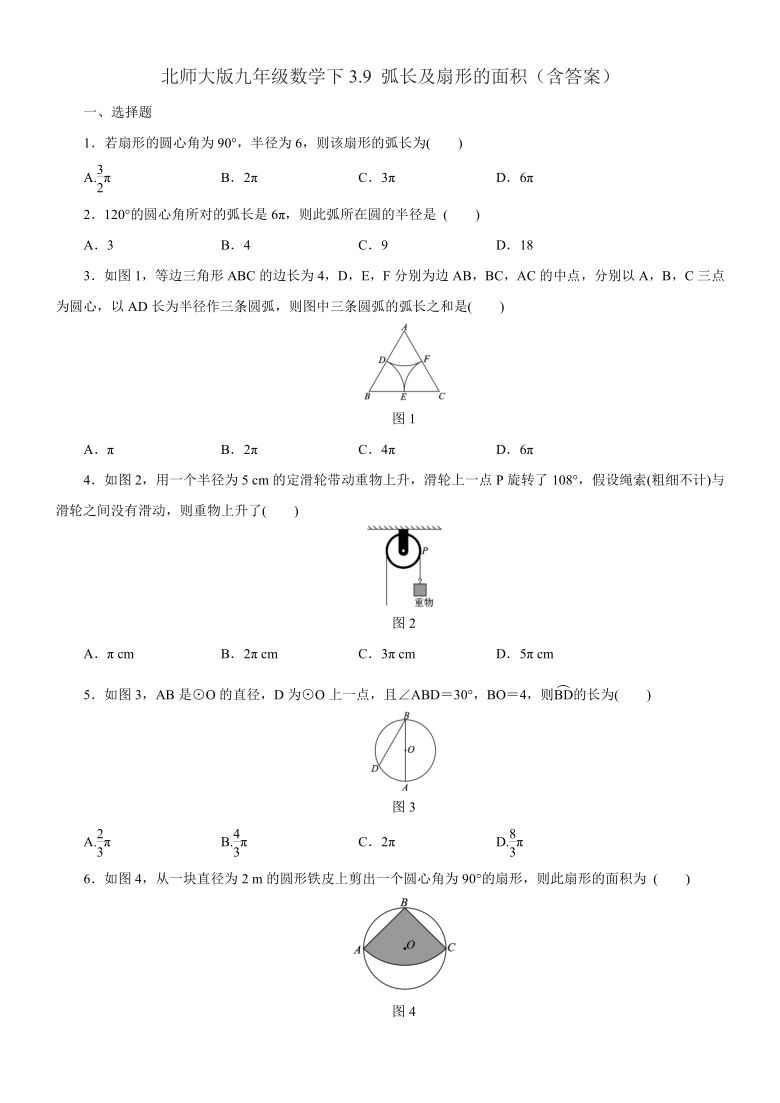 | |
| 格式 | docx | ||
| 文件大小 | 481.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 00:00:38 | ||
图片预览




文档简介
北师大版九年级数学下3.9
弧长及扇形的面积(含答案)
一、选择题
1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )
A.π
B.2π
C.3π
D.6π
2.120°的圆心角所对的弧长是6π,则此弧所在圆的半径是
( )
A.3
B.4
C.9
D.18
3.如图1,等边三角形ABC的边长为4,D,E,F分别为边AB,BC,AC的中点,分别以A,B,C三点为圆心,以AD长为半径作三条圆弧,则图中三条圆弧的弧长之和是( )
图1
A.π
B.2π
C.4π
D.6π
4.如图2,用一个半径为5
cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
图2
A.π
cm
B.2π
cm
C.3π
cm
D.5π
cm
5.如图3,AB是⊙O的直径,D为⊙O上一点,且∠ABD=30°,BO=4,则的长为( )
图3
A.π
B.π
C.2π
D.π
6.如图4,从一块直径为2
m的圆形铁皮上剪出一个圆心角为90°的扇形,则此扇形的面积为
( )
图4
A.
m2
B.π
m2
C.π
m2
D.2π
m2
二、填空题
7.一个扇形的弧长是11π
cm,半径是18
cm,则此扇形的圆心角是________度.
8.如图5,分别以正三角形的3个顶点为圆心,边长为半径画弧,三段弧围成的图形称为莱洛三角形.若正三角形的边长为6
cm,则该莱洛三角形的周长为________
cm.
图5
9.如图6,在边长为4的正方形ABCD中,先以点A为圆心,AD长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则两弧之间的阴影部分的面积是________.(结果保留π)
图6
10.如图7,在Rt△ABC中,∠ACB=90°,AC=BC=2,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积为________.
图7
三、解答题
11.如图8,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连接BC.
(1)求证:AE=ED;
(2)若AB=10,∠CBD=36°,求的长.
图8
12.如图9,四边形ABCD是正方形,以边AB为直径作⊙O,点E在BC边上,连接AE交⊙O于点F,连接BF并延长交CD于点G.
(1)求证:△ABE≌△BCG;
(2)若∠AEB=55°,OA=3,求的长(结果保留π).
图9
13.如图10,已知AB,CD是⊙O的两条直径,AE∥CD交⊙O于点E,连接BE交CD于点F.
(1)求证:=;
(2)若⊙O的半径为6,AE=6
,求图中阴影部分的面积.
图10
附加题
研究型在学习扇形的面积公式时,同学们推得S扇形=,并通过比较扇形面积公式与弧长公式l=,得出扇形面积的另一种计算方法S扇形=lR.接着老师让同学们解决以下两个问题:
问题
Ⅰ:求弧长为4π,圆心角为120°的扇形的面积.
问题Ⅱ:某小区设计的花坛形状如图11中的阴影部分,已知弧AB和弧CD所在圆的圆心都是点O,弧AB的长为l1,弧CD的长为l2,AC=BD=d,求花坛的面积.
(1)请你解答问题Ⅰ.
(2)在解完问题
Ⅱ
后的全班交流中,一名同学发现扇形面积公式S扇形=lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S=(l1+l2)d.他的猜想正确吗?如果正确,请写出推导过程;如果不正确,请说明理由.
图11
参考答案
1.[答案]
C
2.[解析]
C 根据弧长公式l=,得6π=,解得r=9.故选C.
3.[解析]
B 依题意知,图中三条圆弧的弧长之和=×3=2π.故选B.
4.[解析]
C 根据题意,得l==3π(cm),则重物上升了3π
cm.故选C.
5.
[解析]
D 如图,连接OD.
∵∠ABD=30°,∴∠AOD=2∠ABD=60°,∴∠BOD=120°,∴的长==.故选D.
6.[解析]
A 连接AC,如图.
∵从一块直径为2
m的圆形铁皮上剪出一个圆心角为90°的扇形,即∠ABC=90°,
∴AC为直径,即AC=2
m,AB=BC.
∵AB2+BC2=22,
∴AB=BC=
m,
∴这个扇形的面积为=(m2).
7.[答案]
110
[解析]
根据l===11π,
解得n=110.
故答案为110.
8.[答案]
6π
[解析]
该莱洛三角形的周长=3×=6π(cm).故答案为6π.
9.[答案]
2π
10.[答案]
[解析]
∵∠ACB=90°,AC=BC=2,
∴AB=2
,
∴S扇形BAD==.
又∵Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,
∴Rt△ADE≌Rt△ABC,
∴S阴影部分=S△ADE+S扇形BAD-S△ABC=S扇形BAD=.
故答案为.
11.解:(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°.
∵OC∥BD,∴∠AEO=∠ADB=90°,
即OC⊥AD,∴AE=ED.
(2)∵OC⊥AD,∴=,
∴∠ABC=∠CBD=36°,
∴∠AOC=2∠ABC=2×36°=72°,
∴的长==2π.
12.解:(1)证明:∵四边形ABCD是正方形,AB为⊙O的直径,
∴AB=BC,∠ABE=∠BCG=∠AFB=90°,
∴∠BAF+∠ABF=90°,∠ABF+∠EBF=90°,
∴∠EBF=∠BAF,即∠CBG=∠BAE.
在△ABE与△BCG中,∵∠BAE=∠CBG,AB=BC,∠ABE=∠BCG,
∴△ABE≌△BCG(ASA).
(2)如图,连接OF.∵∠ABE=90°,∠AEB=55°,
∴∠BAE=90°-55°=35°,
∴∠BOF=2∠BAE=70°.
∵OA=3,∴的长==.
13.解:(1)证明:如图,连接OE.
∵OA=OE,
∴∠OAE=∠OEA.
∵AE∥CD,
∴∠OEA=∠EOD,∠OAE=∠BOD,
∴∠EOD=∠BOD,
∴=.
(2)如图,过点O作OH⊥AE于点H,
则AH=HE=AE=3
,cos∠OAH===,
∴∠OAH=30°,
∴OH=OA=3,∠AOH=60°,
∴∠AOE=120°,
∴S阴影部分=-×6
×3=12π-9
.
附加题
[解析]
根据扇形面积公式、弧长公式之间的关系,结合已知条件推出结果.
解:(1)∵扇形的弧长为4π,圆心角为120°,
∴扇形的半径R1==6,
∴S扇形=lR1=×4π×6=12π.
(2)他的猜想正确.
设大扇形的半径为R,小扇形的半径为r,圆心角的度数为n°,
则由弧长公式得R=,r=,
∴花坛的面积为
l1R-l2r
=·l1·-·l2·
=
=(l1+l2)(l1-l2)
=·(l1+l2)(R-r)
=(l1+l2)(R-r)=(l1+l2)d.
故他的猜想正确.
弧长及扇形的面积(含答案)
一、选择题
1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )
A.π
B.2π
C.3π
D.6π
2.120°的圆心角所对的弧长是6π,则此弧所在圆的半径是
( )
A.3
B.4
C.9
D.18
3.如图1,等边三角形ABC的边长为4,D,E,F分别为边AB,BC,AC的中点,分别以A,B,C三点为圆心,以AD长为半径作三条圆弧,则图中三条圆弧的弧长之和是( )
图1
A.π
B.2π
C.4π
D.6π
4.如图2,用一个半径为5
cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
图2
A.π
cm
B.2π
cm
C.3π
cm
D.5π
cm
5.如图3,AB是⊙O的直径,D为⊙O上一点,且∠ABD=30°,BO=4,则的长为( )
图3
A.π
B.π
C.2π
D.π
6.如图4,从一块直径为2
m的圆形铁皮上剪出一个圆心角为90°的扇形,则此扇形的面积为
( )
图4
A.
m2
B.π
m2
C.π
m2
D.2π
m2
二、填空题
7.一个扇形的弧长是11π
cm,半径是18
cm,则此扇形的圆心角是________度.
8.如图5,分别以正三角形的3个顶点为圆心,边长为半径画弧,三段弧围成的图形称为莱洛三角形.若正三角形的边长为6
cm,则该莱洛三角形的周长为________
cm.
图5
9.如图6,在边长为4的正方形ABCD中,先以点A为圆心,AD长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则两弧之间的阴影部分的面积是________.(结果保留π)
图6
10.如图7,在Rt△ABC中,∠ACB=90°,AC=BC=2,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积为________.
图7
三、解答题
11.如图8,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连接BC.
(1)求证:AE=ED;
(2)若AB=10,∠CBD=36°,求的长.
图8
12.如图9,四边形ABCD是正方形,以边AB为直径作⊙O,点E在BC边上,连接AE交⊙O于点F,连接BF并延长交CD于点G.
(1)求证:△ABE≌△BCG;
(2)若∠AEB=55°,OA=3,求的长(结果保留π).
图9
13.如图10,已知AB,CD是⊙O的两条直径,AE∥CD交⊙O于点E,连接BE交CD于点F.
(1)求证:=;
(2)若⊙O的半径为6,AE=6
,求图中阴影部分的面积.
图10
附加题
研究型在学习扇形的面积公式时,同学们推得S扇形=,并通过比较扇形面积公式与弧长公式l=,得出扇形面积的另一种计算方法S扇形=lR.接着老师让同学们解决以下两个问题:
问题
Ⅰ:求弧长为4π,圆心角为120°的扇形的面积.
问题Ⅱ:某小区设计的花坛形状如图11中的阴影部分,已知弧AB和弧CD所在圆的圆心都是点O,弧AB的长为l1,弧CD的长为l2,AC=BD=d,求花坛的面积.
(1)请你解答问题Ⅰ.
(2)在解完问题
Ⅱ
后的全班交流中,一名同学发现扇形面积公式S扇形=lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S=(l1+l2)d.他的猜想正确吗?如果正确,请写出推导过程;如果不正确,请说明理由.
图11
参考答案
1.[答案]
C
2.[解析]
C 根据弧长公式l=,得6π=,解得r=9.故选C.
3.[解析]
B 依题意知,图中三条圆弧的弧长之和=×3=2π.故选B.
4.[解析]
C 根据题意,得l==3π(cm),则重物上升了3π
cm.故选C.
5.
[解析]
D 如图,连接OD.
∵∠ABD=30°,∴∠AOD=2∠ABD=60°,∴∠BOD=120°,∴的长==.故选D.
6.[解析]
A 连接AC,如图.
∵从一块直径为2
m的圆形铁皮上剪出一个圆心角为90°的扇形,即∠ABC=90°,
∴AC为直径,即AC=2
m,AB=BC.
∵AB2+BC2=22,
∴AB=BC=
m,
∴这个扇形的面积为=(m2).
7.[答案]
110
[解析]
根据l===11π,
解得n=110.
故答案为110.
8.[答案]
6π
[解析]
该莱洛三角形的周长=3×=6π(cm).故答案为6π.
9.[答案]
2π
10.[答案]
[解析]
∵∠ACB=90°,AC=BC=2,
∴AB=2
,
∴S扇形BAD==.
又∵Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,
∴Rt△ADE≌Rt△ABC,
∴S阴影部分=S△ADE+S扇形BAD-S△ABC=S扇形BAD=.
故答案为.
11.解:(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°.
∵OC∥BD,∴∠AEO=∠ADB=90°,
即OC⊥AD,∴AE=ED.
(2)∵OC⊥AD,∴=,
∴∠ABC=∠CBD=36°,
∴∠AOC=2∠ABC=2×36°=72°,
∴的长==2π.
12.解:(1)证明:∵四边形ABCD是正方形,AB为⊙O的直径,
∴AB=BC,∠ABE=∠BCG=∠AFB=90°,
∴∠BAF+∠ABF=90°,∠ABF+∠EBF=90°,
∴∠EBF=∠BAF,即∠CBG=∠BAE.
在△ABE与△BCG中,∵∠BAE=∠CBG,AB=BC,∠ABE=∠BCG,
∴△ABE≌△BCG(ASA).
(2)如图,连接OF.∵∠ABE=90°,∠AEB=55°,
∴∠BAE=90°-55°=35°,
∴∠BOF=2∠BAE=70°.
∵OA=3,∴的长==.
13.解:(1)证明:如图,连接OE.
∵OA=OE,
∴∠OAE=∠OEA.
∵AE∥CD,
∴∠OEA=∠EOD,∠OAE=∠BOD,
∴∠EOD=∠BOD,
∴=.
(2)如图,过点O作OH⊥AE于点H,
则AH=HE=AE=3
,cos∠OAH===,
∴∠OAH=30°,
∴OH=OA=3,∠AOH=60°,
∴∠AOE=120°,
∴S阴影部分=-×6
×3=12π-9
.
附加题
[解析]
根据扇形面积公式、弧长公式之间的关系,结合已知条件推出结果.
解:(1)∵扇形的弧长为4π,圆心角为120°,
∴扇形的半径R1==6,
∴S扇形=lR1=×4π×6=12π.
(2)他的猜想正确.
设大扇形的半径为R,小扇形的半径为r,圆心角的度数为n°,
则由弧长公式得R=,r=,
∴花坛的面积为
l1R-l2r
=·l1·-·l2·
=
=(l1+l2)(l1-l2)
=·(l1+l2)(R-r)
=(l1+l2)(R-r)=(l1+l2)d.
故他的猜想正确.
