沪科版九年级数学下册 第二十四章 圆巩固检测题(Word版 含答案)
文档属性
| 名称 | 沪科版九年级数学下册 第二十四章 圆巩固检测题(Word版 含答案) | 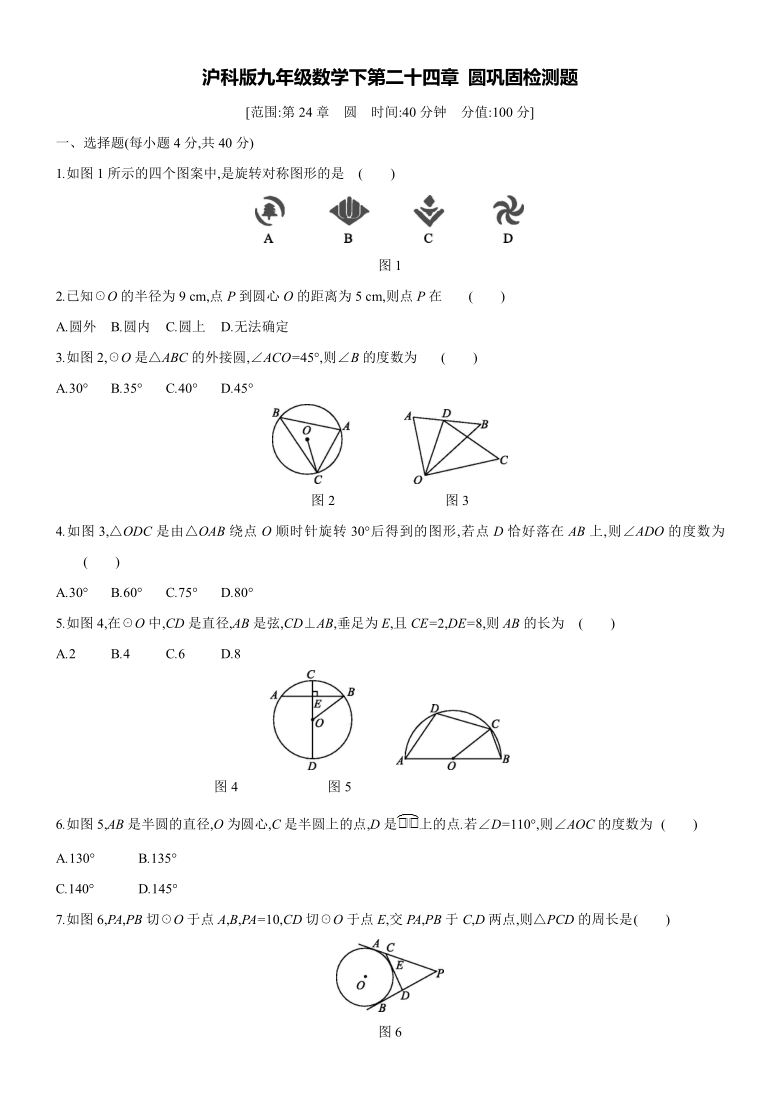 | |
| 格式 | doc | ||
| 文件大小 | 602.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 00:02:28 | ||
图片预览




文档简介
沪科版九年级数学下第二十四章 圆巩固检测题
[范围:第24章 圆 时间:40分钟 分值:100分]
一、选择题(每小题4分,共40分)
1.如图1所示的四个图案中,是旋转对称图形的是 ( )
图1
2.已知☉O的半径为9 cm,点P到圆心O的距离为5 cm,则点P在 ( )
A.圆外 B.圆内 C.圆上 D.无法确定
3.如图2,☉O是△ABC的外接圆,∠ACO=45°,则∠B的度数为 ( )
A.30° B.35° C.40° D.45°
图2 图3
4.如图3,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,则∠ADO的度数为 ( )
A.30° B.60° C.75° D.80°
5.如图4,在☉O中,CD是直径,AB是弦,CD⊥AB,垂足为E,且CE=2,DE=8,则AB的长为 ( )
A.2 B.4 C.6 D.8
图4 图5
6.如图5,AB是半圆的直径,O为圆心,C是半圆上的点,D是上的点.若∠D=110°,则∠AOC的度数为 ( )
A.130° B.135°
C.140° D.145°
7.如图6,PA,PB切☉O于点A,B,PA=10,CD切☉O于点E,交PA,PB于C,D两点,则△PCD的周长是 ( )
图6
A.10 B.18 C.20 D.22
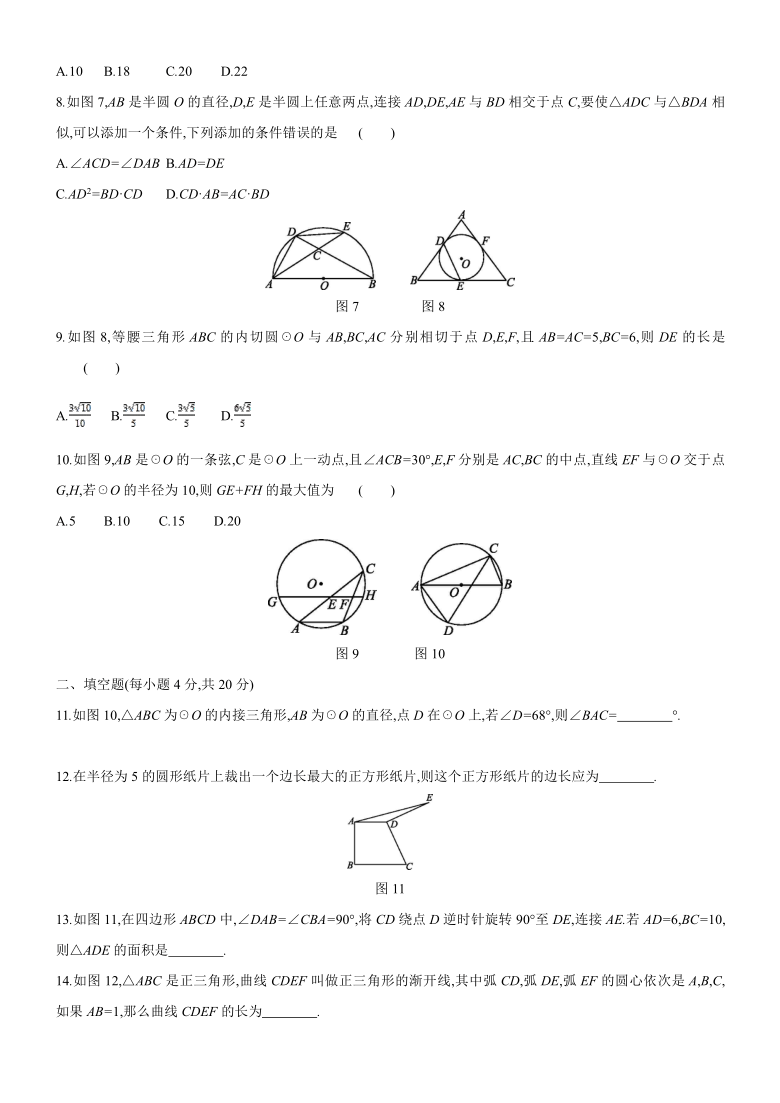
8.如图7,AB是半圆O的直径,D,E是半圆上任意两点,连接AD,DE,AE与BD相交于点C,要使△ADC与△BDA相似,可以添加一个条件,下列添加的条件错误的是 ( )
A.∠ACD=∠DAB B.AD=DE
C.AD2=BD·CD D.CD·AB=AC·BD
图7 图8
9.如图8,等腰三角形ABC的内切圆☉O与AB,BC,AC分别相切于点D,E,F,且AB=AC=5,BC=6,则DE的长是 ( )
A. B. C. D.
10.如图9,AB是☉O的一条弦,C是☉O上一动点,且∠ACB=30°,E,F分别是AC,BC的中点,直线EF与☉O交于点G,H,若☉O的半径为10,则GE+FH的最大值为 ( )
A.5 B.10 C.15 D.20
图9 图10
二、填空题(每小题4分,共20分)
11.如图10,△ABC为☉O的内接三角形,AB为☉O的直径,点D在☉O上,若∠D=68°,则∠BAC= °.?
12.在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为 .?
图11
13.如图11,在四边形ABCD中,∠DAB=∠CBA=90°,将CD绕点D逆时针旋转90°至DE,连接AE.若AD=6,BC=10,则△ADE的面积是 .?
14.如图12,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中弧CD,弧DE,弧EF的圆心依次是A,B,C,如果AB=1,那么曲线CDEF的长为 .?
图12 图13
15.如图13,AB为☉O的直径,P为AB延长线上的一点,过点P作☉O的切线PE,切点为M,过A,B两点分别作PE的垂线AC,BD,垂足分别为C,D,连接AM,则下列结论正确的是 .(写出所有正确结论的序号)?
①AM平分∠CAB;②AM2=AC·AB;③若AB=4,∠APE=30°,则的长为;④若AC=3,BD=1,则有CM=DM=.
三、解答题(共40分)
16.(12分)如图14,在☉O中,弦AB与CD相交于点E,AB=CD,连接AD,BC.
求证:(1)=;
(2)AE=CE.
图14
17.(14分)如图15,AB是☉O的切线,B为切点,圆心O在AC上,∠A=30°,D为的中点.
(1)求证:AB=BC;
(2)试判断四边形BOCD的形状,并说明理由.
图15
18.(14分)如图16,在Rt△ABC中,∠B=90°,∠BAC的平分线AD交BC于点D,点E在AC上,以AE为直径的☉O经过点D.
(1)求证:①BC是☉O的切线;
②CD2=CE·CA.
(2)若F是劣弧AD的中点,且CE=3,试求阴影部分的面积.
图16
参考答案
1.D
2.B [解析] 因为点P到圆心的距离为5 cm,小于圆的半径9 cm,所以点P在圆内.
3.D [解析] 连接OA,可得∠AOC=90°,∴∠B=45°.
4.C
5.D [解析] ∵CE=2,DE=8,∴CD=10,
∴OC=OB=5,∴OE=3.
∵AB⊥CD,∴在Rt△OBE中,根据勾股定理,得BE=4,∴AB=2BE=8.
故选D.
6.C 7.C 8.D
9.D [解析] 如图,连接OA,OE,OB,OB交DE于点H.
∵等腰三角形ABC的内切圆☉O与AB,BC,AC分别相切于点D,E,F,
∴OA平分∠BAC,OE⊥BC,OD⊥AB,BE=BD.
∵AB=AC,∴OA⊥BC,∴点A,O,E共线,即AE⊥BC,∴BE=CE=3.
在Rt△ABE中,AE==4.
∵BD=BE=3,∴AD=2.
设☉O的半径为r,则OD=OE=r,AO=4-r.
在Rt△AOD中,r2+22=(4-r)2,解得r=.
在Rt△BOE中,OB==.
∵BE=BD,OE=OD,∴OB垂直平分DE,
∴DH=EH,OB⊥DE.
∵S△BOE=HE·OB=OE·BE,
∴HE===,
∴DE=2HE=.
故选D.
10.C [解析] 如图,连接OA,OB.
∵∠ACB=30°,
∴∠AOB=2∠ACB=60°.
∵OA=OB,
∴△AOB为等边三角形.
∵☉O的半径为10,
∴AB=OA=OB=10.
∵E,F分别是AC,BC的中点,
∴EF=AB=5.
要求GE+FH有最大值,即求GE+FH+EF(弦GH)的最大值.
∵当弦GH是圆的直径时,它有最大值,为10×2=20,
∴GE+FH的最大值为20-5=15.故选C.
11.22 [解析] ∵∠B与∠D都是所对的圆周角,∴∠B=∠D=68°.
∵AB为☉O的直径,∴∠ACB=90°,
∴∠BAC=90°-∠B=90°-68°=22°.
12.5
13.12 [解析] 如图,过点D作DH⊥BC于点H,过点E作EF⊥AD交AD的延长线于点F,
则HC=BC-BH=BC-AD=10-6=4.
∵将CD绕点D逆时针旋转90°至DE,
∴△DHC≌△DFE,
∴EF=HC=4,且∠EFA=∠DHC=90°,
∴S△ADE=AD·EF=×6×4=12.
14.4π [解析] ==,==,==2π,
所以曲线CDEF的长=++2π=4π.
15.①②④ [解析] 如图,连接OM,BM.
∵PE是☉O的切线,
∴OM⊥PE.
∵AC⊥PE,
∴AC∥OM,
∴∠CAM=∠AMO.
∵OA=OM,
∴∠AMO=∠MAO,
∴∠CAM=∠MAO,
∴AM平分∠CAB.①正确.
∵AB为☉O的直径,
∴∠AMB=90°=∠ACM.
∵∠CAM=∠MAO,
∴△AMC∽△ABM,
∴=,
∴AM2=AC·AB.②正确.
∵∠P=30°,
∴∠MOP=60°.
∵AB=4,
∴半径r=2,
∴==π.③错误.
∵BD∥OM∥AC,OA=OB,
∴CM=DM.
∵∠CAM+∠AMC=90°,∠AMC+∠BMD=90°,∴∠CAM=∠BMD.
∵∠ACM=∠BDM=90°,∴△ACM∽△MDB,∴=,
∴CM·DM=3×1=3.∴CM=DM=.④正确.
综上所述,结论正确的有①②④.
16.证明:(1)如图,连接AO,BO,CO,DO.
∵AB=CD,
∴∠AOB=∠COD,
∴∠AOD=∠BOC,
∴=.
(2)∵=,∴AD=BC.
∵=,∴∠ADC=∠ABC.
又∵∠AED=∠CEB,∴△ADE≌△CBE,
∴AE=CE.
17.解:(1)证明:∵AB是☉O的切线,
∴∠OBA=90°,∴∠AOB=90°-30°=60°.
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OCB=∠AOB=30°=∠A,
∴AB=BC.
(2)四边形BOCD是菱形.
理由:如图,连接OD,交BC于点M.
∵D为的中点,∴OD垂直平分BC.
在Rt△OMC中,
∵∠OCB=30°,∴OC=2OM=OD,
∴OM=MD,
∴四边形BOCD是菱形.
18.解:(1)证明:①如图,连接OD.
∵AD是∠BAC的平分线,
∴∠DAB=∠DAO.
∵OD=OA,
∴∠DAO=∠ODA,则∠DAB=∠ODA,
∴DO∥AB.
而∠B=90°,∴∠ODB=90°.
又∵OD是☉O的半径,∴BC是☉O的切线.
②如图,连接DE.
∵BC是☉O的切线,
∴∠ODC=90°,即∠CDE+∠ODE=90°.
∵AE为☉O的直径,∴∠EDA=90°,即∠ADO+∠ODE=90°,
∴∠CDE=∠ADO.
∵OA=OD,∴∠ADO=∠DAC,
∴∠CDE=∠DAC.
又∵∠C=∠C,
∴△CDE∽△CAD,∴=,
∴CD2=CE·CA.
(2)如图,连接DF,OF.
∵F是劣弧AD的中点,
∴OF是DA的垂直平分线,
∴DF=AF,
∴∠FDA=∠FAD.
∵DO∥AB,
∴∠ODA=∠FAD,
∴∠ODA=∠DAO=∠FDA=∠FAD,
易知AF=DF=OA=OD,
∴△OFD,△OFA是等边三角形,
∴∠DOF=∠FOA=60°,∴∠DOC=60°,
则∠C=30°,
∴OD=OC=(OE+CE).
又∵OE=OD,∴CE=OE=3.
易知S阴影=S扇形DOF,
∴S阴影=×π×32=.
[范围:第24章 圆 时间:40分钟 分值:100分]
一、选择题(每小题4分,共40分)
1.如图1所示的四个图案中,是旋转对称图形的是 ( )
图1
2.已知☉O的半径为9 cm,点P到圆心O的距离为5 cm,则点P在 ( )
A.圆外 B.圆内 C.圆上 D.无法确定
3.如图2,☉O是△ABC的外接圆,∠ACO=45°,则∠B的度数为 ( )
A.30° B.35° C.40° D.45°
图2 图3
4.如图3,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,则∠ADO的度数为 ( )
A.30° B.60° C.75° D.80°
5.如图4,在☉O中,CD是直径,AB是弦,CD⊥AB,垂足为E,且CE=2,DE=8,则AB的长为 ( )
A.2 B.4 C.6 D.8
图4 图5
6.如图5,AB是半圆的直径,O为圆心,C是半圆上的点,D是上的点.若∠D=110°,则∠AOC的度数为 ( )
A.130° B.135°
C.140° D.145°
7.如图6,PA,PB切☉O于点A,B,PA=10,CD切☉O于点E,交PA,PB于C,D两点,则△PCD的周长是 ( )
图6
A.10 B.18 C.20 D.22
8.如图7,AB是半圆O的直径,D,E是半圆上任意两点,连接AD,DE,AE与BD相交于点C,要使△ADC与△BDA相似,可以添加一个条件,下列添加的条件错误的是 ( )
A.∠ACD=∠DAB B.AD=DE
C.AD2=BD·CD D.CD·AB=AC·BD
图7 图8
9.如图8,等腰三角形ABC的内切圆☉O与AB,BC,AC分别相切于点D,E,F,且AB=AC=5,BC=6,则DE的长是 ( )
A. B. C. D.
10.如图9,AB是☉O的一条弦,C是☉O上一动点,且∠ACB=30°,E,F分别是AC,BC的中点,直线EF与☉O交于点G,H,若☉O的半径为10,则GE+FH的最大值为 ( )
A.5 B.10 C.15 D.20
图9 图10
二、填空题(每小题4分,共20分)
11.如图10,△ABC为☉O的内接三角形,AB为☉O的直径,点D在☉O上,若∠D=68°,则∠BAC= °.?
12.在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为 .?
图11
13.如图11,在四边形ABCD中,∠DAB=∠CBA=90°,将CD绕点D逆时针旋转90°至DE,连接AE.若AD=6,BC=10,则△ADE的面积是 .?
14.如图12,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中弧CD,弧DE,弧EF的圆心依次是A,B,C,如果AB=1,那么曲线CDEF的长为 .?
图12 图13
15.如图13,AB为☉O的直径,P为AB延长线上的一点,过点P作☉O的切线PE,切点为M,过A,B两点分别作PE的垂线AC,BD,垂足分别为C,D,连接AM,则下列结论正确的是 .(写出所有正确结论的序号)?
①AM平分∠CAB;②AM2=AC·AB;③若AB=4,∠APE=30°,则的长为;④若AC=3,BD=1,则有CM=DM=.
三、解答题(共40分)
16.(12分)如图14,在☉O中,弦AB与CD相交于点E,AB=CD,连接AD,BC.
求证:(1)=;
(2)AE=CE.
图14
17.(14分)如图15,AB是☉O的切线,B为切点,圆心O在AC上,∠A=30°,D为的中点.
(1)求证:AB=BC;
(2)试判断四边形BOCD的形状,并说明理由.
图15
18.(14分)如图16,在Rt△ABC中,∠B=90°,∠BAC的平分线AD交BC于点D,点E在AC上,以AE为直径的☉O经过点D.
(1)求证:①BC是☉O的切线;
②CD2=CE·CA.
(2)若F是劣弧AD的中点,且CE=3,试求阴影部分的面积.
图16
参考答案
1.D
2.B [解析] 因为点P到圆心的距离为5 cm,小于圆的半径9 cm,所以点P在圆内.
3.D [解析] 连接OA,可得∠AOC=90°,∴∠B=45°.
4.C
5.D [解析] ∵CE=2,DE=8,∴CD=10,
∴OC=OB=5,∴OE=3.
∵AB⊥CD,∴在Rt△OBE中,根据勾股定理,得BE=4,∴AB=2BE=8.
故选D.
6.C 7.C 8.D
9.D [解析] 如图,连接OA,OE,OB,OB交DE于点H.
∵等腰三角形ABC的内切圆☉O与AB,BC,AC分别相切于点D,E,F,
∴OA平分∠BAC,OE⊥BC,OD⊥AB,BE=BD.
∵AB=AC,∴OA⊥BC,∴点A,O,E共线,即AE⊥BC,∴BE=CE=3.
在Rt△ABE中,AE==4.
∵BD=BE=3,∴AD=2.
设☉O的半径为r,则OD=OE=r,AO=4-r.
在Rt△AOD中,r2+22=(4-r)2,解得r=.
在Rt△BOE中,OB==.
∵BE=BD,OE=OD,∴OB垂直平分DE,
∴DH=EH,OB⊥DE.
∵S△BOE=HE·OB=OE·BE,
∴HE===,
∴DE=2HE=.
故选D.
10.C [解析] 如图,连接OA,OB.
∵∠ACB=30°,
∴∠AOB=2∠ACB=60°.
∵OA=OB,
∴△AOB为等边三角形.
∵☉O的半径为10,
∴AB=OA=OB=10.
∵E,F分别是AC,BC的中点,
∴EF=AB=5.
要求GE+FH有最大值,即求GE+FH+EF(弦GH)的最大值.
∵当弦GH是圆的直径时,它有最大值,为10×2=20,
∴GE+FH的最大值为20-5=15.故选C.
11.22 [解析] ∵∠B与∠D都是所对的圆周角,∴∠B=∠D=68°.
∵AB为☉O的直径,∴∠ACB=90°,
∴∠BAC=90°-∠B=90°-68°=22°.
12.5
13.12 [解析] 如图,过点D作DH⊥BC于点H,过点E作EF⊥AD交AD的延长线于点F,
则HC=BC-BH=BC-AD=10-6=4.
∵将CD绕点D逆时针旋转90°至DE,
∴△DHC≌△DFE,
∴EF=HC=4,且∠EFA=∠DHC=90°,
∴S△ADE=AD·EF=×6×4=12.
14.4π [解析] ==,==,==2π,
所以曲线CDEF的长=++2π=4π.
15.①②④ [解析] 如图,连接OM,BM.
∵PE是☉O的切线,
∴OM⊥PE.
∵AC⊥PE,
∴AC∥OM,
∴∠CAM=∠AMO.
∵OA=OM,
∴∠AMO=∠MAO,
∴∠CAM=∠MAO,
∴AM平分∠CAB.①正确.
∵AB为☉O的直径,
∴∠AMB=90°=∠ACM.
∵∠CAM=∠MAO,
∴△AMC∽△ABM,
∴=,
∴AM2=AC·AB.②正确.
∵∠P=30°,
∴∠MOP=60°.
∵AB=4,
∴半径r=2,
∴==π.③错误.
∵BD∥OM∥AC,OA=OB,
∴CM=DM.
∵∠CAM+∠AMC=90°,∠AMC+∠BMD=90°,∴∠CAM=∠BMD.
∵∠ACM=∠BDM=90°,∴△ACM∽△MDB,∴=,
∴CM·DM=3×1=3.∴CM=DM=.④正确.
综上所述,结论正确的有①②④.
16.证明:(1)如图,连接AO,BO,CO,DO.
∵AB=CD,
∴∠AOB=∠COD,
∴∠AOD=∠BOC,
∴=.
(2)∵=,∴AD=BC.
∵=,∴∠ADC=∠ABC.
又∵∠AED=∠CEB,∴△ADE≌△CBE,
∴AE=CE.
17.解:(1)证明:∵AB是☉O的切线,
∴∠OBA=90°,∴∠AOB=90°-30°=60°.
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OCB=∠AOB=30°=∠A,
∴AB=BC.
(2)四边形BOCD是菱形.
理由:如图,连接OD,交BC于点M.
∵D为的中点,∴OD垂直平分BC.
在Rt△OMC中,
∵∠OCB=30°,∴OC=2OM=OD,
∴OM=MD,
∴四边形BOCD是菱形.
18.解:(1)证明:①如图,连接OD.
∵AD是∠BAC的平分线,
∴∠DAB=∠DAO.
∵OD=OA,
∴∠DAO=∠ODA,则∠DAB=∠ODA,
∴DO∥AB.
而∠B=90°,∴∠ODB=90°.
又∵OD是☉O的半径,∴BC是☉O的切线.
②如图,连接DE.
∵BC是☉O的切线,
∴∠ODC=90°,即∠CDE+∠ODE=90°.
∵AE为☉O的直径,∴∠EDA=90°,即∠ADO+∠ODE=90°,
∴∠CDE=∠ADO.
∵OA=OD,∴∠ADO=∠DAC,
∴∠CDE=∠DAC.
又∵∠C=∠C,
∴△CDE∽△CAD,∴=,
∴CD2=CE·CA.
(2)如图,连接DF,OF.
∵F是劣弧AD的中点,
∴OF是DA的垂直平分线,
∴DF=AF,
∴∠FDA=∠FAD.
∵DO∥AB,
∴∠ODA=∠FAD,
∴∠ODA=∠DAO=∠FDA=∠FAD,
易知AF=DF=OA=OD,
∴△OFD,△OFA是等边三角形,
∴∠DOF=∠FOA=60°,∴∠DOC=60°,
则∠C=30°,
∴OD=OC=(OE+CE).
又∵OE=OD,∴CE=OE=3.
易知S阴影=S扇形DOF,
∴S阴影=×π×32=.
