苏科版数学八年级上册 3.1 勾股定理 作业题 (word版 无答案)
文档属性
| 名称 | 苏科版数学八年级上册 3.1 勾股定理 作业题 (word版 无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 138.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 16:32:18 | ||
图片预览

文档简介
勾股定理作业
知识点
勾股定理:
勾股定理逆定理:
选择题:
1.已知一个Rt△的两边长分别为3和4,则第三边长的平方是( )
A、25
B、14
C、7
D、7或25
2.下列各组数中,以a,b,c为边的三角形不是Rt△的是( )
A、a=1.5,b=2,c=3
B、a=7,b=24,c=25
C、a=6,b=8,c=10
D、a=3,b=4,c=5
3.若线段a,b,c组成Rt△,则它们的比为( )
A、2∶3∶4
B、3∶4∶6
C、5∶12∶13
D、4∶6∶7
4.Rt△一直角边的长为11,另两边为自然数,则Rt△的周长为( )
A、121
B、120
C、132
D、不能确定
5.如果Rt△两直角边的比为5∶12,则斜边上的高与斜边的比为( )
A、60∶13
B、5∶12
C、12∶13
D、60∶169
6.如果Rt△的两直角边长分别为n2-1,2n(n>1),那么它的斜边长是( )
A、2n
B、n+1
C、n2-1
D、n2+1
7.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是( )
A、24cm2
B、36cm2
C、48cm2
D、60cm2
8.等腰三角形底边上的高为8,周长为32,则三角形的面积为( )
A、56
B、48
C、40
D、32
9.三角形的三边长为(a+b)2=c2+2ab,则这个三角形是(
)
A.
等边三角形;
B.
钝角三角形;
C.
直角三角形;
D.
锐角三角形.
10.某市在旧城改造中,计划在市内一块如图所示的三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )
A、450a元
B、225a
元
C、150a元
D、300a元
11.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A、6cm2
B、8cm2
C、10cm2
D、12cm2
12.已知,如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )
A、25海里
B、30海里
C、35海里
D、40海里
13.
若一个直角三角形的一条直角边长是7cm,另一条直角边比斜边短1cm,则斜边长为
(
)
A.18
cm
B.20
cm
C.24
cm
D.25
cm
14.一条河的宽度处处相等,小强想从河的南岸横游到北岸去,由于水流影响,小强上岸地点偏离目标地点200m,他在水中实际游了520m,那么该河的宽度为(
)
A.440
m
B.460
m
C.480
m
D.
500
m
填空题:
1.在Rt△ABC中,∠C=90°,①若a=5,b=12,则c=___________;②若a=15,c=25,则b=___________;③若c=61,b=60,则a=__________;④若a∶b=3∶4,c=10则SRt△ABC=________。
2.直角三角形两直角边长分别为5和12,则它斜边上的高为__________。
3.在平静的湖面上,有一支红莲,高出水面1米,阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的水平距离为2米,问这里水深是________m。
4.已知两条线段的长为5cm和12cm,当第三条线段的长为????????????????
cm时,这三条线段能组成一个直角三角形.
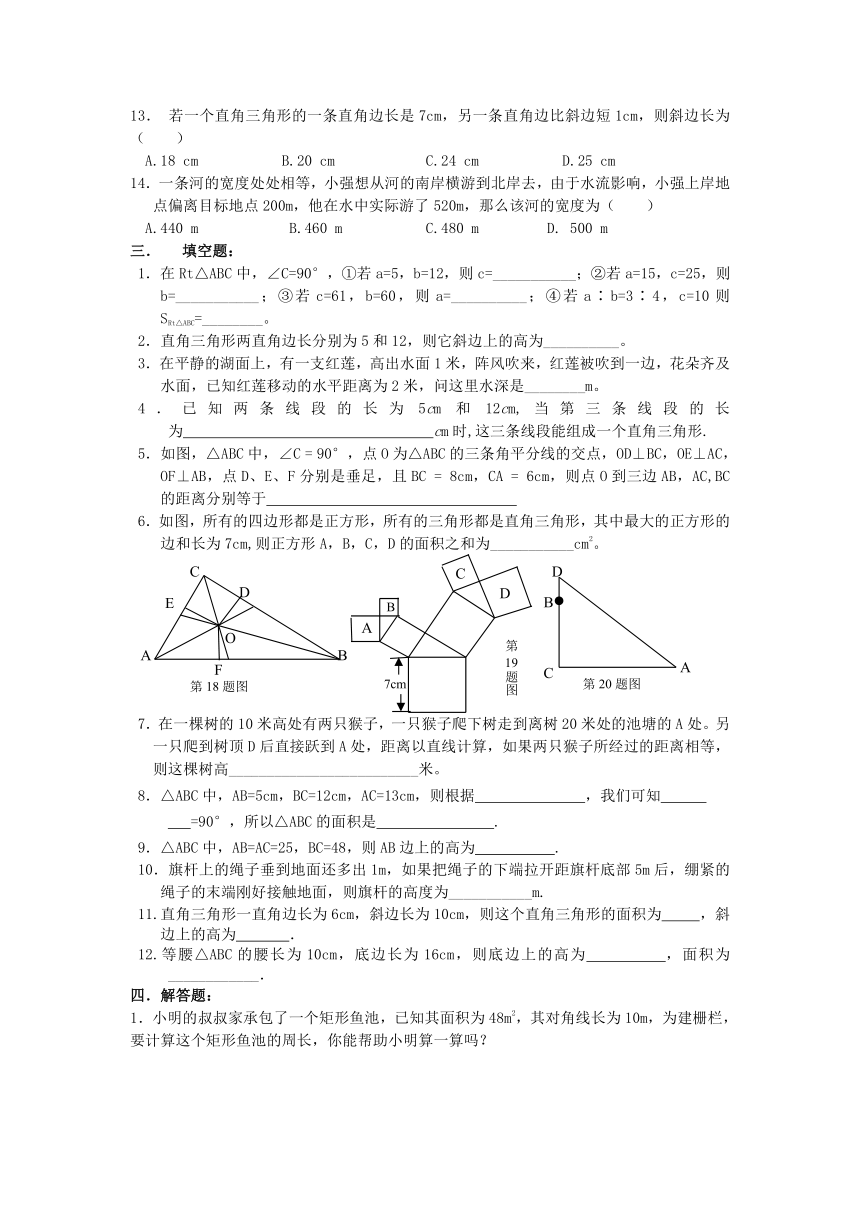
5.如图,△ABC中,∠C
=
90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且BC
=
8cm,CA
=
6cm,则点O到三边AB,AC,BC的距离分别等于
6.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边和长为7cm,则正方形A,B,C,D的面积之和为___________cm2。
7.在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A处。另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高_________________________米。
8.△ABC中,AB=5cm,BC=12cm,AC=13cm,则根据
,我们可知
=90°,所以△ABC的面积是
.
9.△ABC中,AB=AC=25,BC=48,则AB边上的高为
.
10.旗杆上的绳子垂到地面还多出1m,如果把绳子的下端拉开距旗杆底部5m后,绷紧的绳子的末端刚好接触地面,则旗杆的高度为___________m.
11.直角三角形一直角边长为6cm,斜边长为10cm,则这个直角三角形的面积为
,斜边上的高为
.
12.等腰△ABC的腰长为10cm,底边长为16cm,则底边上的高为
,面积为____________.
四.解答题:
1.小明的叔叔家承包了一个矩形鱼池,已知其面积为48m2,其对角线长为10m,为建栅栏,要计算这个矩形鱼池的周长,你能帮助小明算一算吗?
2.如图,铁路上A,B两点相距25km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
3.已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,求四边形ABCD的面积。
4.如图,在Rt△ABC中,∠C=90°,∠CAD=∠DAB,CD=1.5,BD=2.5,求AC的长.
5.如图,在边长为c的正方形中,有四个斜边为c的全等直角三角形,已知其直角边长为a,b(a>b).利用这个图试说明勾股定理?
6.如图,在△ABC中,AB=AC,P为BC上任意一点,请用学过的知识说明:AB2-AP2=PB×PC。
7.欲将一根长129cm的木棒放在长、高、宽分别是40cm、30cm、120cm的木箱中,能放得进去吗?请画图标字母说明理由.
8.已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,满足a2+b2+c2+338=10a+24b+26c。
试判断△ABC的形状。
9.已知:如图,AD=4,CD=3,∠ADC=90°,AB=13,BC=12.求图形的面积.
10.
A城气象台测的台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内时受台风影响的区域。
(1)A城是否受到这次台风的影响?说明理由。
(2)若A城受到这次台风的影响,那么A城遭受这次台风影响有多长时间?
知识点
勾股定理:
勾股定理逆定理:
选择题:
1.已知一个Rt△的两边长分别为3和4,则第三边长的平方是( )
A、25
B、14
C、7
D、7或25
2.下列各组数中,以a,b,c为边的三角形不是Rt△的是( )
A、a=1.5,b=2,c=3
B、a=7,b=24,c=25
C、a=6,b=8,c=10
D、a=3,b=4,c=5
3.若线段a,b,c组成Rt△,则它们的比为( )
A、2∶3∶4
B、3∶4∶6
C、5∶12∶13
D、4∶6∶7
4.Rt△一直角边的长为11,另两边为自然数,则Rt△的周长为( )
A、121
B、120
C、132
D、不能确定
5.如果Rt△两直角边的比为5∶12,则斜边上的高与斜边的比为( )
A、60∶13
B、5∶12
C、12∶13
D、60∶169
6.如果Rt△的两直角边长分别为n2-1,2n(n>1),那么它的斜边长是( )
A、2n
B、n+1
C、n2-1
D、n2+1
7.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是( )
A、24cm2
B、36cm2
C、48cm2
D、60cm2
8.等腰三角形底边上的高为8,周长为32,则三角形的面积为( )
A、56
B、48
C、40
D、32
9.三角形的三边长为(a+b)2=c2+2ab,则这个三角形是(
)
A.
等边三角形;
B.
钝角三角形;
C.
直角三角形;
D.
锐角三角形.
10.某市在旧城改造中,计划在市内一块如图所示的三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )
A、450a元
B、225a
元
C、150a元
D、300a元
11.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A、6cm2
B、8cm2
C、10cm2
D、12cm2
12.已知,如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )
A、25海里
B、30海里
C、35海里
D、40海里
13.
若一个直角三角形的一条直角边长是7cm,另一条直角边比斜边短1cm,则斜边长为
(
)
A.18
cm
B.20
cm
C.24
cm
D.25
cm
14.一条河的宽度处处相等,小强想从河的南岸横游到北岸去,由于水流影响,小强上岸地点偏离目标地点200m,他在水中实际游了520m,那么该河的宽度为(
)
A.440
m
B.460
m
C.480
m
D.
500
m
填空题:
1.在Rt△ABC中,∠C=90°,①若a=5,b=12,则c=___________;②若a=15,c=25,则b=___________;③若c=61,b=60,则a=__________;④若a∶b=3∶4,c=10则SRt△ABC=________。
2.直角三角形两直角边长分别为5和12,则它斜边上的高为__________。
3.在平静的湖面上,有一支红莲,高出水面1米,阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的水平距离为2米,问这里水深是________m。
4.已知两条线段的长为5cm和12cm,当第三条线段的长为????????????????
cm时,这三条线段能组成一个直角三角形.
5.如图,△ABC中,∠C
=
90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且BC
=
8cm,CA
=
6cm,则点O到三边AB,AC,BC的距离分别等于
6.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边和长为7cm,则正方形A,B,C,D的面积之和为___________cm2。
7.在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A处。另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高_________________________米。
8.△ABC中,AB=5cm,BC=12cm,AC=13cm,则根据
,我们可知
=90°,所以△ABC的面积是
.
9.△ABC中,AB=AC=25,BC=48,则AB边上的高为
.
10.旗杆上的绳子垂到地面还多出1m,如果把绳子的下端拉开距旗杆底部5m后,绷紧的绳子的末端刚好接触地面,则旗杆的高度为___________m.
11.直角三角形一直角边长为6cm,斜边长为10cm,则这个直角三角形的面积为
,斜边上的高为
.
12.等腰△ABC的腰长为10cm,底边长为16cm,则底边上的高为
,面积为____________.
四.解答题:
1.小明的叔叔家承包了一个矩形鱼池,已知其面积为48m2,其对角线长为10m,为建栅栏,要计算这个矩形鱼池的周长,你能帮助小明算一算吗?
2.如图,铁路上A,B两点相距25km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
3.已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,求四边形ABCD的面积。
4.如图,在Rt△ABC中,∠C=90°,∠CAD=∠DAB,CD=1.5,BD=2.5,求AC的长.
5.如图,在边长为c的正方形中,有四个斜边为c的全等直角三角形,已知其直角边长为a,b(a>b).利用这个图试说明勾股定理?
6.如图,在△ABC中,AB=AC,P为BC上任意一点,请用学过的知识说明:AB2-AP2=PB×PC。
7.欲将一根长129cm的木棒放在长、高、宽分别是40cm、30cm、120cm的木箱中,能放得进去吗?请画图标字母说明理由.
8.已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,满足a2+b2+c2+338=10a+24b+26c。
试判断△ABC的形状。
9.已知:如图,AD=4,CD=3,∠ADC=90°,AB=13,BC=12.求图形的面积.
10.
A城气象台测的台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内时受台风影响的区域。
(1)A城是否受到这次台风的影响?说明理由。
(2)若A城受到这次台风的影响,那么A城遭受这次台风影响有多长时间?
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
