2020年秋人教版九年级数学上册专题小练习十九 24.4 弧长及扇形的面积(word版 含答案)
文档属性
| 名称 | 2020年秋人教版九年级数学上册专题小练习十九 24.4 弧长及扇形的面积(word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 162.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 16:35:11 | ||
图片预览

文档简介
2020年人教版九年级数学上册专题小练习
《圆-扇形弧长与面积》
、选择题
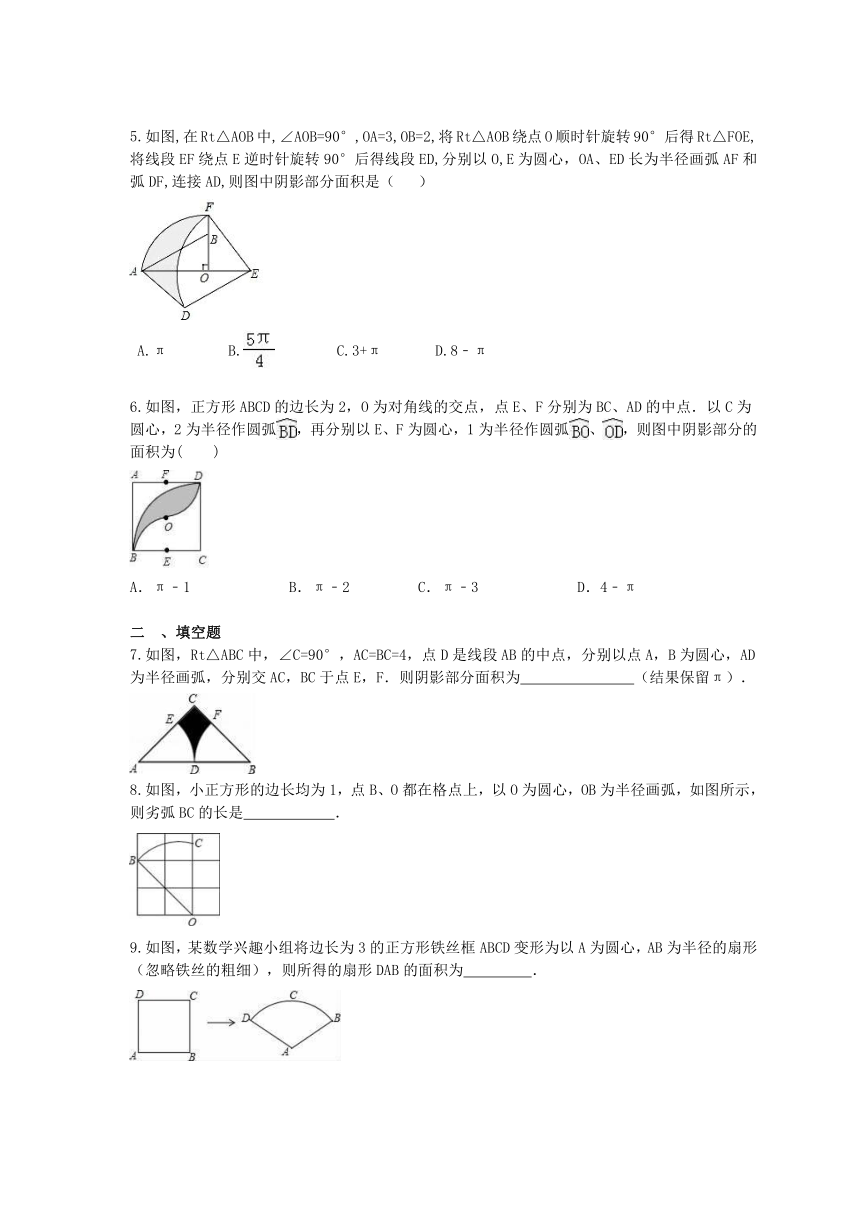
图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是(
)
A.甲先到B点
B.乙先到B点
C.甲、乙同时到B
D.无法确定
如图,圆锥底面半径为rcm,母线长为10cm,其侧面展开图是圆心角为216°的扇形,则r的值为(
)
A.3
B.6
C.3π
D.6π
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长( )
A.2π
B.π
C.
D.
如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(阴影部分)面积之和为S2,则=(
)
A.
B.
C.
D.1
如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是(
)
A.π
B.
C.3+π
D.8﹣π
如图,正方形ABCD的边长为2,O为对角线的交点,点E、F分别为BC、AD的中点.以C为圆心,2为半径作圆弧,再分别以E、F为圆心,1为半径作圆弧、,则图中阴影部分的面积为( )
A.π﹣1??????
B.π﹣2????
C.π﹣3??????
D.4﹣π
、填空题
如图,Rt△ABC中,∠C=90°,AC=BC=4,点D是线段AB的中点,分别以点A,B为圆心,AD为半径画弧,分别交AC,BC于点E,F.则阴影部分面积为 ?????
(结果保留π).
如图,小正方形的边长均为1,点B、O都在格点上,以O为圆心,OB为半径画弧,如图所示,则劣弧BC的长是 .
如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为
.
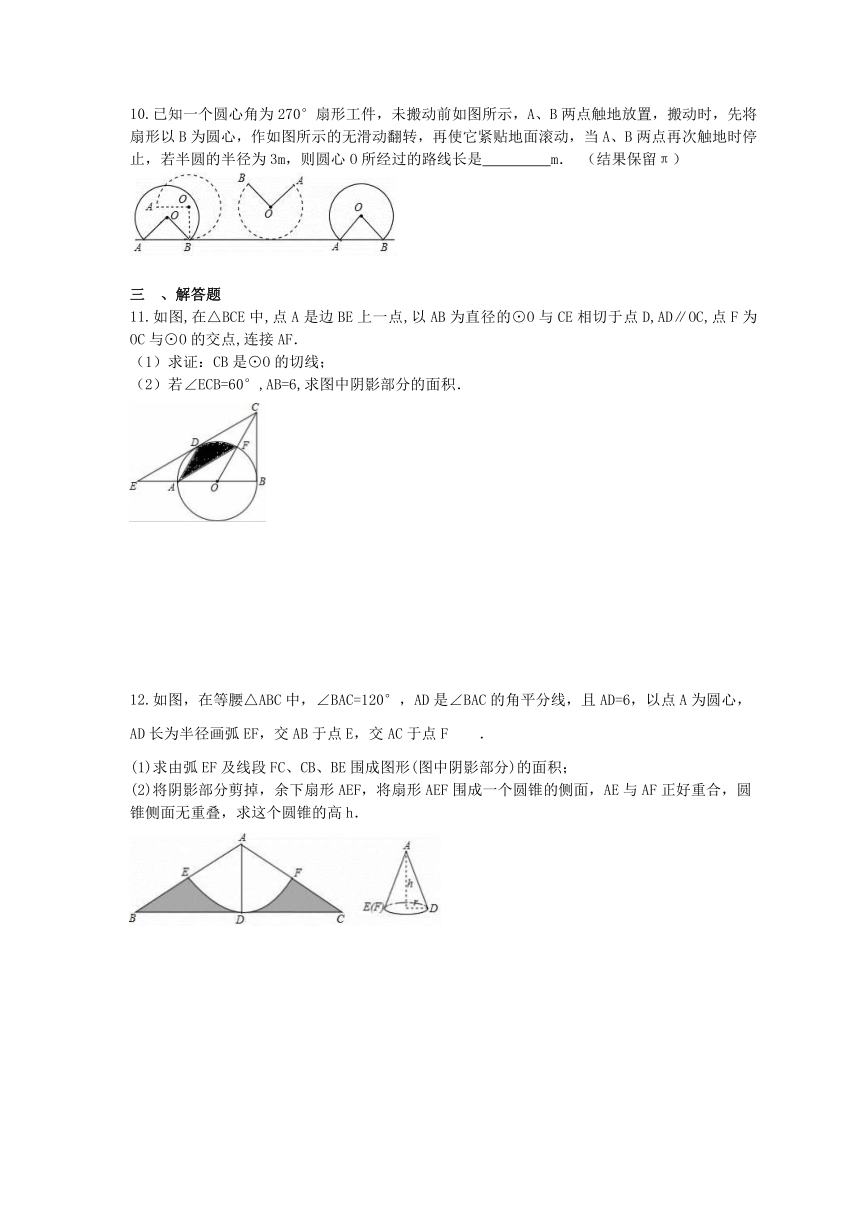
已知一个圆心角为270°扇形工件,未搬动前如图所示,A、B两点触地放置,搬动时,先将扇形以B为圆心,作如图所示的无滑动翻转,再使它紧贴地面滚动,当A、B两点再次触地时停止,若半圆的半径为3m,则圆心O所经过的路线长是
????m.
(结果保留π)
、解答题
如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.
(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;
(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
参考答案
C
A
B.
B
D
答案为:B
答案为:8﹣2π.
答案为:π.
答案为:9.
答案为:6π?
?
【解答】(1)证明:连接OD,与AF相交于点G,
∵CE与⊙O相切于点D,∴OD⊥CE,∴∠CDO=90°,
∵AD∥OC,∴∠ADO=∠DOC,∠DAO=∠BOC,
∵OA=OD,∴∠ADO=∠DAO,∴∠DOC=∠BOC,
在△CDO和△CBO中,,∴△CDO≌△CBO,
∴∠CBO=∠CDO=90°,∴CB是⊙O的切线.
(2)由(1)可知∠DOA=∠BCO,∠DOC=∠BOC,
∵∠ECB=60°,∴∠DCO=∠BCO=∠ECB=30°,∴∠DOC=∠BOC=60°∴∠DOA=60°,
∵OA=OD,∴△OAD是等边三角形,∴AD=OD=OF,∵∠GOF=∠ADO,
在△ADG和△FOG中,,∴△ADG≌△FOG,∴S△ADG=S△FOG,
∵AB=6,∴⊙O的半径r=3,∴S阴=S扇形ODF==π.
解:∵在等腰△ABC中,∠BAC=120°,
∴∠B=30°,
∵AD是∠BAC的角平分线,
∴AD⊥BC,BD=CD,
∴BD=AD=6,
∴BC=2BD=12,
∴由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积
=S△ABC﹣S扇形EAF=×6×12﹣=36﹣12π;
(2)设圆锥的底面圆的半径为r,
根据题意得2πr=,解得r=2,
这个圆锥的高h==4.
《圆-扇形弧长与面积》
、选择题
图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是(
)
A.甲先到B点
B.乙先到B点
C.甲、乙同时到B
D.无法确定
如图,圆锥底面半径为rcm,母线长为10cm,其侧面展开图是圆心角为216°的扇形,则r的值为(
)
A.3
B.6
C.3π
D.6π
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长( )
A.2π
B.π
C.
D.
如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(阴影部分)面积之和为S2,则=(
)
A.
B.
C.
D.1
如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是(
)
A.π
B.
C.3+π
D.8﹣π
如图,正方形ABCD的边长为2,O为对角线的交点,点E、F分别为BC、AD的中点.以C为圆心,2为半径作圆弧,再分别以E、F为圆心,1为半径作圆弧、,则图中阴影部分的面积为( )
A.π﹣1??????
B.π﹣2????
C.π﹣3??????
D.4﹣π
、填空题
如图,Rt△ABC中,∠C=90°,AC=BC=4,点D是线段AB的中点,分别以点A,B为圆心,AD为半径画弧,分别交AC,BC于点E,F.则阴影部分面积为 ?????
(结果保留π).
如图,小正方形的边长均为1,点B、O都在格点上,以O为圆心,OB为半径画弧,如图所示,则劣弧BC的长是 .
如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为
.
已知一个圆心角为270°扇形工件,未搬动前如图所示,A、B两点触地放置,搬动时,先将扇形以B为圆心,作如图所示的无滑动翻转,再使它紧贴地面滚动,当A、B两点再次触地时停止,若半圆的半径为3m,则圆心O所经过的路线长是
????m.
(结果保留π)
、解答题
如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.
(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;
(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
参考答案
C
A
B.
B
D
答案为:B
答案为:8﹣2π.
答案为:π.
答案为:9.
答案为:6π?
?
【解答】(1)证明:连接OD,与AF相交于点G,
∵CE与⊙O相切于点D,∴OD⊥CE,∴∠CDO=90°,
∵AD∥OC,∴∠ADO=∠DOC,∠DAO=∠BOC,
∵OA=OD,∴∠ADO=∠DAO,∴∠DOC=∠BOC,
在△CDO和△CBO中,,∴△CDO≌△CBO,
∴∠CBO=∠CDO=90°,∴CB是⊙O的切线.
(2)由(1)可知∠DOA=∠BCO,∠DOC=∠BOC,
∵∠ECB=60°,∴∠DCO=∠BCO=∠ECB=30°,∴∠DOC=∠BOC=60°∴∠DOA=60°,
∵OA=OD,∴△OAD是等边三角形,∴AD=OD=OF,∵∠GOF=∠ADO,
在△ADG和△FOG中,,∴△ADG≌△FOG,∴S△ADG=S△FOG,
∵AB=6,∴⊙O的半径r=3,∴S阴=S扇形ODF==π.
解:∵在等腰△ABC中,∠BAC=120°,
∴∠B=30°,
∵AD是∠BAC的角平分线,
∴AD⊥BC,BD=CD,
∴BD=AD=6,
∴BC=2BD=12,
∴由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积
=S△ABC﹣S扇形EAF=×6×12﹣=36﹣12π;
(2)设圆锥的底面圆的半径为r,
根据题意得2πr=,解得r=2,
这个圆锥的高h==4.
同课章节目录
