华东师大版九年级数学下册第27章 圆中考试题训练(Word版 含答案)
文档属性
| 名称 | 华东师大版九年级数学下册第27章 圆中考试题训练(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 267.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 19:32:33 | ||
图片预览

文档简介
第27章
圆
中考演练
一、选择题
1.[2020·泸州]
如图27-Y-1,在☉O中,=,∠ABC=70°,则∠BOC的度数为
( )
A.100°
B.90°
C.80°
D.70°
图27-Y-1
图27-Y-2
2.[2020·哈尔滨]
如图27-Y-2,AB为☉O的切线,A为切点,OB交☉O于点C,点D在☉O上,连结AD,CD,OA.若∠ADC=35°,则∠ABO的度数为
( )
A.25°
B.20°
C.30°
D.35°
3.[2020·滨州]
在☉O中,直径AB=15,弦DE⊥AB于点C,若OC∶OB=3∶5,则DE的长为( )
A.6
B.9
C.12
D.15
4.[2019·凉山州改编]
有下列命题:①两条长度相等的弧叫做等弧;②过直径的端点所作的垂线是圆的切线;③相等的圆心角所对的弧相等;④平分弦的直径垂直于弦.其中真命题的个数为
( )
A.1
B.2
C.3
D.4
5.[2020·常德]
一个圆锥的底面半径r=10,高h=20,则这个圆锥的侧面积是
( )
A.100π
B.200π
C.100π
D.200π
6.[2019·宁波]
如图27-Y-3所示,矩形纸片ABCD中,AD=6
cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为
( )
图27-Y-3
A.3.5
cm
B.4
cm
C.4.5
cm
D.5
cm
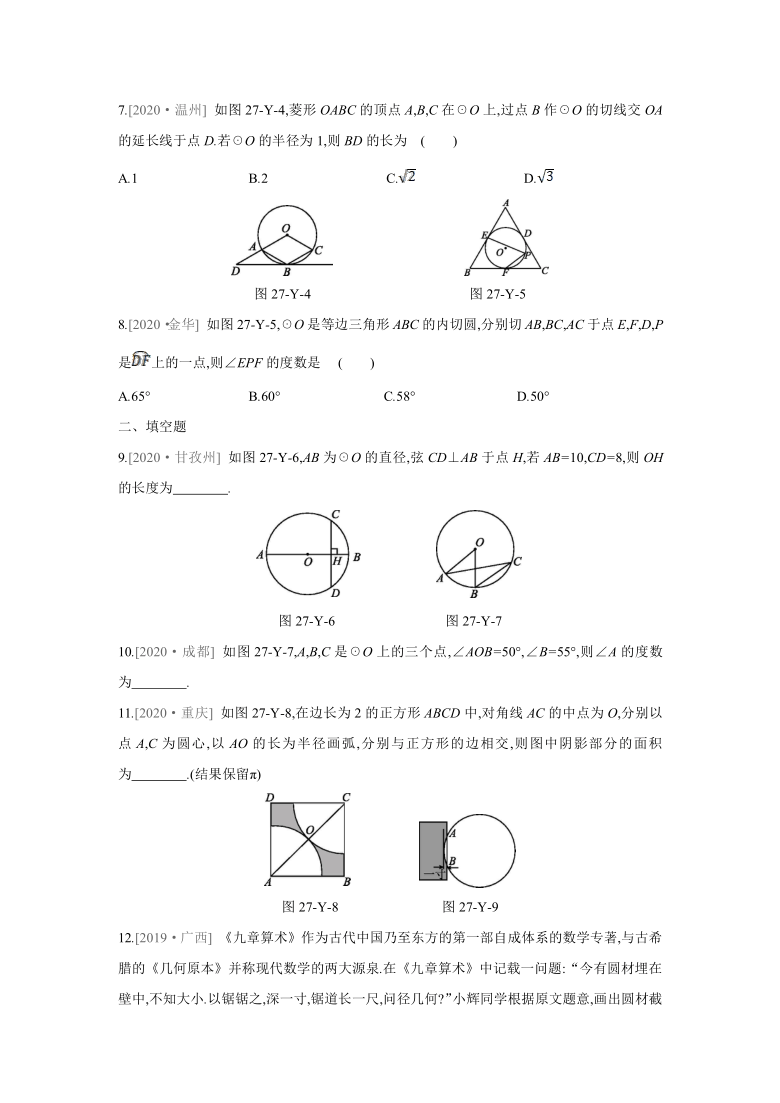
7.[2020·温州]
如图27-Y-4,菱形OABC的顶点A,B,C在☉O上,过点B作☉O的切线交OA的延长线于点D.若☉O的半径为1,则BD的长为
( )
A.1
B.2
C.
D.
图27-Y-4
图27-Y-5
8.[2020·金华]
如图27-Y-5,☉O是等边三角形ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是上的一点,则∠EPF的度数是
( )
A.65°
B.60°
C.58°
D.50°
二、填空题
9.[2020·甘孜州]
如图27-Y-6,AB为☉O的直径,弦CD⊥AB于点H,若AB=10,CD=8,则OH的长度为 .?
图27-Y-6
图27-Y-7
10.[2020·成都]
如图27-Y-7,A,B,C是☉O上的三个点,∠AOB=50°,∠B=55°,则∠A的度数为 .?
11.[2020·重庆]
如图27-Y-8,在边长为2的正方形ABCD中,对角线AC的中点为O,分别以点A,C为圆心,以AO的长为半径画弧,分别与正方形的边相交,则图中阴影部分的面积为 .(结果保留π)?
图27-Y-8
图27-Y-9
12.[2019·广西]
《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载一问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图27-Y-9所示,已知:锯口深为1寸,锯道AB=1尺(1尺=10寸),则该圆材的直径为
寸.?
13.[2019·眉山]
如图27-Y-10,在Rt△AOB中,OA=OB=4,☉O的半径为2,P是AB边上的动点,过点P作☉O的一条切线PQ(Q为切点),则线段PQ长的最小值为 .?
图27-Y-10
三、解答题
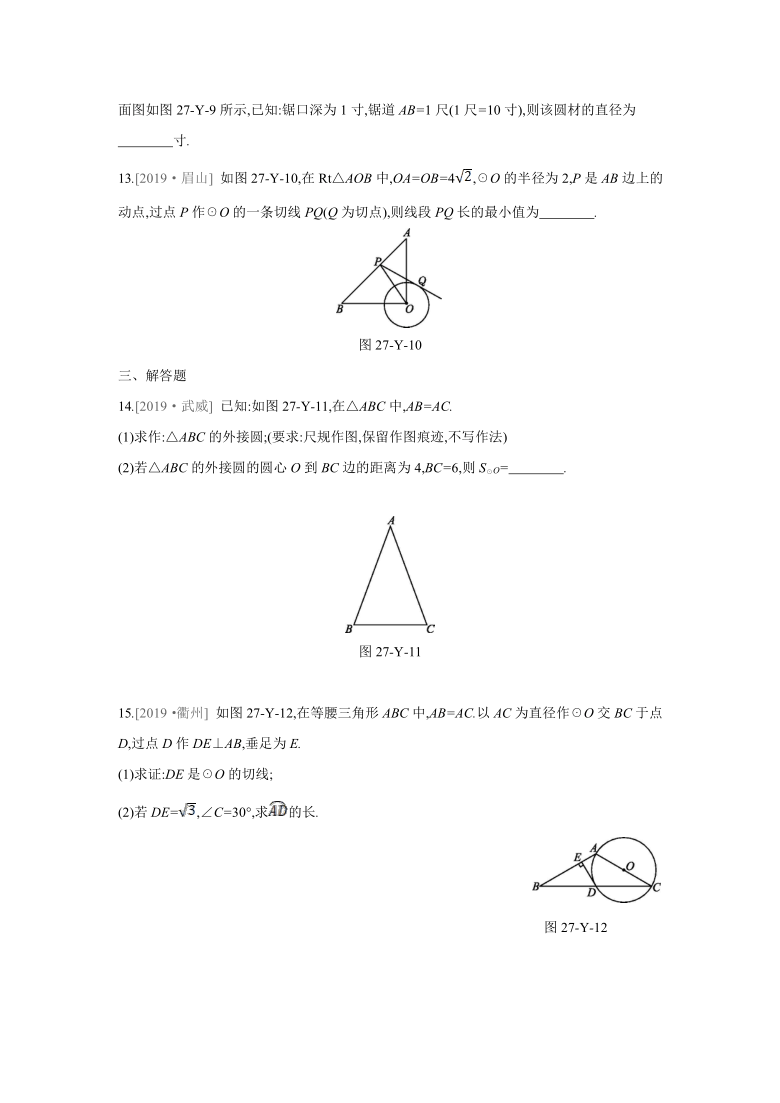
14.[2019·武威]
已知:如图27-Y-11,在△ABC中,AB=AC.
(1)求作:△ABC的外接圆;(要求:尺规作图,保留作图痕迹,不写作法)
(2)若△ABC的外接圆的圆心O到BC边的距离为4,BC=6,则S☉O= .?
图27-Y-11
15.[2019·衢州]
如图27-Y-12,在等腰三角形ABC中,AB=AC.以AC为直径作☉O交BC于点D,过点D作DE⊥AB,垂足为E.
(1)求证:DE是☉O的切线;
(2)若DE=,∠C=30°,求的长.
图27-Y-12
16.[2020·遵义]
如图27-Y-13,AB是☉O的直径,C是☉O上一点,∠CAB的平分线AD交于点D,过点D作DE∥BC交AC的延长线于点E.
(1)求证:DE是☉O的切线;
(2)过点D作DF⊥AB于点F,连结BD.若OF=1,BF=2,求BD的长度.
图27-Y-13
17.[2020·温州]
如图27-Y-14,C,D为☉O上两点,且在直径AB两侧,连结CD交AB于点E,G是上一点,∠ADC=∠G.
(1)求证:∠1=∠2;
(2)若点C关于DG的对称点为F,连结CF.当点F落在直径AB上时,CF=10,tan∠1=,求☉O的半径.
图27-Y-14
答案
1.[答案]
C
2.[答案]
B
3.[答案]
C
4.[解析]
A 长度相等的弧不一定能重合,所以不一定是等弧;“过直径的端点所作的垂线”符合过半径外端且与这条半径垂直,所以这样的直线是圆的切线;在同圆或等圆中,相等的圆心角所对的弧相等;平分弦(不是直径)的直径垂直于弦,所以只有②是对的.故选A.
5.[答案]
C
6.[答案]
B
7.[解析]
D 连结OB.∵四边形OABC是菱形,∴OA=AB.
∵OA=OB,∴OA=AB=OB,∴∠AOB=60°.
∵BD是☉O的切线,∴∠DBO=90°.
∵OB=1,∴BD=OB=.
8.[解析]
B 连结OE,OF.∵☉O是△ABC的内切圆,E,F是切点,
∴OE⊥AB,OF⊥BC,∴∠OEB=∠OFB=90°.
∵△ABC是等边三角形,
∴∠B=60°,∴∠EOF=120°,∴∠EPF=∠EOF=60°.
9.[答案]
3
10.[答案]
30°
11.[答案]
4-π
12.[答案]
26
13.[答案]
2
[解析]
连结OQ,如图所示.∵PQ是☉O的切线,∴OQ⊥PQ.
根据勾股定理知PQ2=OP2-OQ2,∴当PO⊥AB时,线段PQ最短.
∵在Rt△AOB中,OA=OB=4,∴AB=OA=8,
∴S△AOB=OA·OB=AB·OP,即OP==4,∴PQ===2.
14.解:(1)如图,☉O即为所求.
(2)25π
15.解:(1)证明:如图,连结OD.
∵OC=OD,AB=AC,∴∠1=∠C,∠C=∠B,∴∠1=∠B.
∵DE⊥AB,∴∠2+∠B=90°,∴∠2+∠1=90°,∴∠ODE=90°.
又∵OD是☉O的半径,∴DE为☉O的切线.
(2)如图,连结AD.∵AC为☉O的直径,∴∠ADC=90°.
又∵AB=AC,∴BD=CD.
∵∠C=30°,∴∠AOD=60°.
∵DE=,∴CD=BD=2.
在Rt△ADC中,cosC===,∴AC=4,∴OA=OC=2,∴=×π×2=π.
16.解:(1)证明:连结OD,如图.
∵AB是☉O的直径,∴∠ACB=∠ADB=90°,
∵OA=OD,∴∠OAD=∠ADO.
∵AD平分∠CAB,∴∠DAE=∠OAD,∴∠ADO=∠DAE,∴OD∥AE.
∵DE∥BC,∴∠E=∠ACB=90°,∴∠ODE=180°-∠E=90°,
∴DE是☉O的切线.
(2)∵OF=1,BF=2,∴OB=3,∴AB=6.
∵DF⊥AB,∴∠DFB=90°,∴∠ADB=∠DFB.
又∵∠DBF=∠ABD,∴△DBF∽△ABD,∴=,∴BD2=BF·AB=2×6=12,∴BD=2.
17.解:(1)证明:∵∠ADC=∠G,∴=.
又∵AB为☉O的直径,∴=,∴∠1=∠2.
(2)如图,连结DF.
∵=,AB是☉O的直径,∴AB⊥CD,CE=DE,∴DF=CF=10.
∵点C,F关于DG对称,∴DC=DF=10,∴DE=5.
∵tan∠1==,∴EB=DE·tan∠1=2.
∵∠1=∠2,∴tan∠2==,∴AE==,∴AB=AE+EB=,∴☉O的半径为.
圆
中考演练
一、选择题
1.[2020·泸州]
如图27-Y-1,在☉O中,=,∠ABC=70°,则∠BOC的度数为
( )
A.100°
B.90°
C.80°
D.70°
图27-Y-1
图27-Y-2
2.[2020·哈尔滨]
如图27-Y-2,AB为☉O的切线,A为切点,OB交☉O于点C,点D在☉O上,连结AD,CD,OA.若∠ADC=35°,则∠ABO的度数为
( )
A.25°
B.20°
C.30°
D.35°
3.[2020·滨州]
在☉O中,直径AB=15,弦DE⊥AB于点C,若OC∶OB=3∶5,则DE的长为( )
A.6
B.9
C.12
D.15
4.[2019·凉山州改编]
有下列命题:①两条长度相等的弧叫做等弧;②过直径的端点所作的垂线是圆的切线;③相等的圆心角所对的弧相等;④平分弦的直径垂直于弦.其中真命题的个数为
( )
A.1
B.2
C.3
D.4
5.[2020·常德]
一个圆锥的底面半径r=10,高h=20,则这个圆锥的侧面积是
( )
A.100π
B.200π
C.100π
D.200π
6.[2019·宁波]
如图27-Y-3所示,矩形纸片ABCD中,AD=6
cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为
( )
图27-Y-3
A.3.5
cm
B.4
cm
C.4.5
cm
D.5
cm
7.[2020·温州]
如图27-Y-4,菱形OABC的顶点A,B,C在☉O上,过点B作☉O的切线交OA的延长线于点D.若☉O的半径为1,则BD的长为
( )
A.1
B.2
C.
D.
图27-Y-4
图27-Y-5
8.[2020·金华]
如图27-Y-5,☉O是等边三角形ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是上的一点,则∠EPF的度数是
( )
A.65°
B.60°
C.58°
D.50°
二、填空题
9.[2020·甘孜州]
如图27-Y-6,AB为☉O的直径,弦CD⊥AB于点H,若AB=10,CD=8,则OH的长度为 .?
图27-Y-6
图27-Y-7
10.[2020·成都]
如图27-Y-7,A,B,C是☉O上的三个点,∠AOB=50°,∠B=55°,则∠A的度数为 .?
11.[2020·重庆]
如图27-Y-8,在边长为2的正方形ABCD中,对角线AC的中点为O,分别以点A,C为圆心,以AO的长为半径画弧,分别与正方形的边相交,则图中阴影部分的面积为 .(结果保留π)?
图27-Y-8
图27-Y-9
12.[2019·广西]
《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载一问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图27-Y-9所示,已知:锯口深为1寸,锯道AB=1尺(1尺=10寸),则该圆材的直径为
寸.?
13.[2019·眉山]
如图27-Y-10,在Rt△AOB中,OA=OB=4,☉O的半径为2,P是AB边上的动点,过点P作☉O的一条切线PQ(Q为切点),则线段PQ长的最小值为 .?
图27-Y-10
三、解答题
14.[2019·武威]
已知:如图27-Y-11,在△ABC中,AB=AC.
(1)求作:△ABC的外接圆;(要求:尺规作图,保留作图痕迹,不写作法)
(2)若△ABC的外接圆的圆心O到BC边的距离为4,BC=6,则S☉O= .?
图27-Y-11
15.[2019·衢州]
如图27-Y-12,在等腰三角形ABC中,AB=AC.以AC为直径作☉O交BC于点D,过点D作DE⊥AB,垂足为E.
(1)求证:DE是☉O的切线;
(2)若DE=,∠C=30°,求的长.
图27-Y-12
16.[2020·遵义]
如图27-Y-13,AB是☉O的直径,C是☉O上一点,∠CAB的平分线AD交于点D,过点D作DE∥BC交AC的延长线于点E.
(1)求证:DE是☉O的切线;
(2)过点D作DF⊥AB于点F,连结BD.若OF=1,BF=2,求BD的长度.
图27-Y-13
17.[2020·温州]
如图27-Y-14,C,D为☉O上两点,且在直径AB两侧,连结CD交AB于点E,G是上一点,∠ADC=∠G.
(1)求证:∠1=∠2;
(2)若点C关于DG的对称点为F,连结CF.当点F落在直径AB上时,CF=10,tan∠1=,求☉O的半径.
图27-Y-14
答案
1.[答案]
C
2.[答案]
B
3.[答案]
C
4.[解析]
A 长度相等的弧不一定能重合,所以不一定是等弧;“过直径的端点所作的垂线”符合过半径外端且与这条半径垂直,所以这样的直线是圆的切线;在同圆或等圆中,相等的圆心角所对的弧相等;平分弦(不是直径)的直径垂直于弦,所以只有②是对的.故选A.
5.[答案]
C
6.[答案]
B
7.[解析]
D 连结OB.∵四边形OABC是菱形,∴OA=AB.
∵OA=OB,∴OA=AB=OB,∴∠AOB=60°.
∵BD是☉O的切线,∴∠DBO=90°.
∵OB=1,∴BD=OB=.
8.[解析]
B 连结OE,OF.∵☉O是△ABC的内切圆,E,F是切点,
∴OE⊥AB,OF⊥BC,∴∠OEB=∠OFB=90°.
∵△ABC是等边三角形,
∴∠B=60°,∴∠EOF=120°,∴∠EPF=∠EOF=60°.
9.[答案]
3
10.[答案]
30°
11.[答案]
4-π
12.[答案]
26
13.[答案]
2
[解析]
连结OQ,如图所示.∵PQ是☉O的切线,∴OQ⊥PQ.
根据勾股定理知PQ2=OP2-OQ2,∴当PO⊥AB时,线段PQ最短.
∵在Rt△AOB中,OA=OB=4,∴AB=OA=8,
∴S△AOB=OA·OB=AB·OP,即OP==4,∴PQ===2.
14.解:(1)如图,☉O即为所求.
(2)25π
15.解:(1)证明:如图,连结OD.
∵OC=OD,AB=AC,∴∠1=∠C,∠C=∠B,∴∠1=∠B.
∵DE⊥AB,∴∠2+∠B=90°,∴∠2+∠1=90°,∴∠ODE=90°.
又∵OD是☉O的半径,∴DE为☉O的切线.
(2)如图,连结AD.∵AC为☉O的直径,∴∠ADC=90°.
又∵AB=AC,∴BD=CD.
∵∠C=30°,∴∠AOD=60°.
∵DE=,∴CD=BD=2.
在Rt△ADC中,cosC===,∴AC=4,∴OA=OC=2,∴=×π×2=π.
16.解:(1)证明:连结OD,如图.
∵AB是☉O的直径,∴∠ACB=∠ADB=90°,
∵OA=OD,∴∠OAD=∠ADO.
∵AD平分∠CAB,∴∠DAE=∠OAD,∴∠ADO=∠DAE,∴OD∥AE.
∵DE∥BC,∴∠E=∠ACB=90°,∴∠ODE=180°-∠E=90°,
∴DE是☉O的切线.
(2)∵OF=1,BF=2,∴OB=3,∴AB=6.
∵DF⊥AB,∴∠DFB=90°,∴∠ADB=∠DFB.
又∵∠DBF=∠ABD,∴△DBF∽△ABD,∴=,∴BD2=BF·AB=2×6=12,∴BD=2.
17.解:(1)证明:∵∠ADC=∠G,∴=.
又∵AB为☉O的直径,∴=,∴∠1=∠2.
(2)如图,连结DF.
∵=,AB是☉O的直径,∴AB⊥CD,CE=DE,∴DF=CF=10.
∵点C,F关于DG对称,∴DC=DF=10,∴DE=5.
∵tan∠1==,∴EB=DE·tan∠1=2.
∵∠1=∠2,∴tan∠2==,∴AE==,∴AB=AE+EB=,∴☉O的半径为.
