苏科版数学八年级上册 6.3一次函数的图像 (2)教案
文档属性
| 名称 | 苏科版数学八年级上册 6.3一次函数的图像 (2)教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 100.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 00:00:00 | ||
图片预览

文档简介
《一次函数的图像(2)》教学设计
一、教学目标
理解一次函数及其图像的相关性质
能熟练画出一次函数图像
进一步培养学生数形结合的意识和能力
经历一次函数及其图像有关性质的探究过程,培养学生探究、合作的能力
二、教学重点:一次函数图像的性质
三、教学难点:一次函数图像性质的探究
四、教学过程
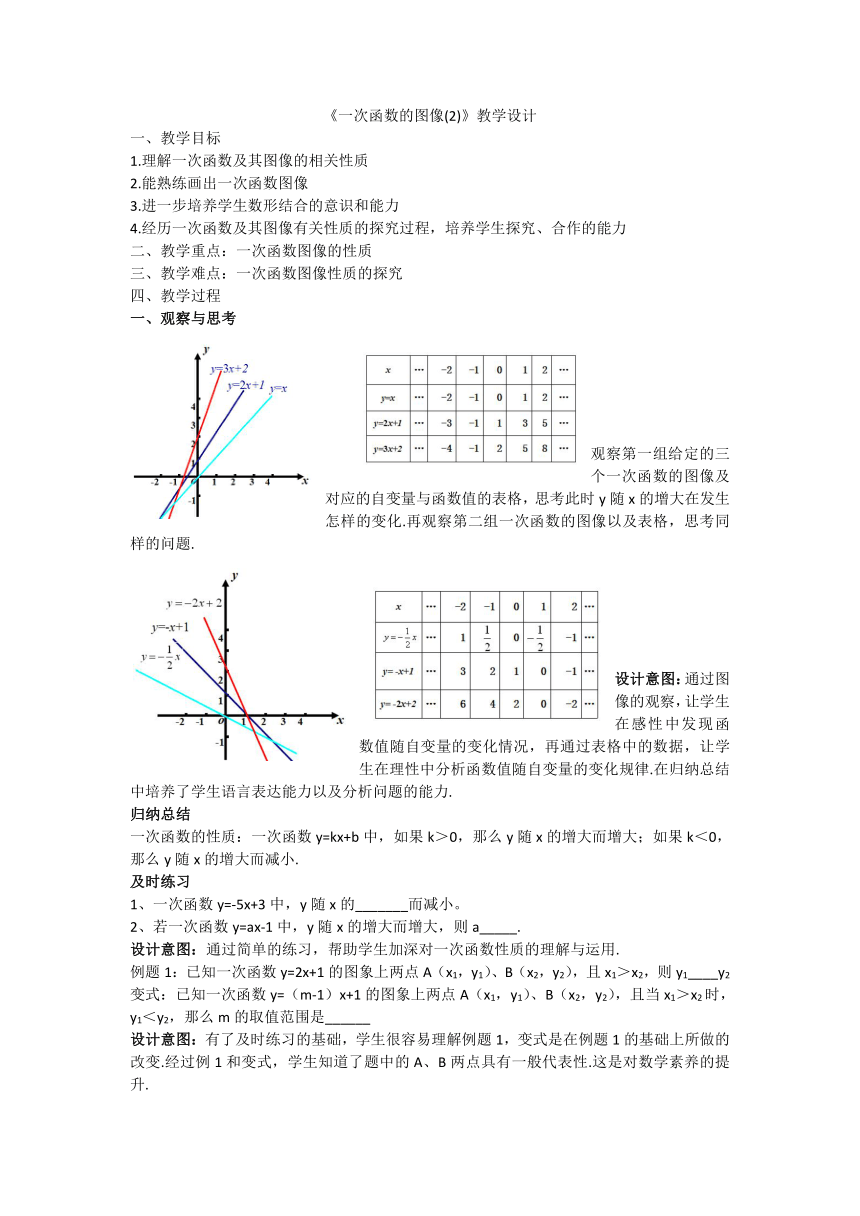
观察与思考
观察第一组给定的三个一次函数的图像及对应的自变量与函数值的表格,思考此时y随x的增大在发生怎样的变化.再观察第二组一次函数的图像以及表格,思考同样的问题.
设计意图:通过图像的观察,让学生在感性中发现函数值随自变量的变化情况,再通过表格中的数据,让学生在理性中分析函数值随自变量的变化规律.在归纳总结中培养了学生语言表达能力以及分析问题的能力.
归纳总结
一次函数的性质:一次函数y=kx+b中,如果k>0,那么y随x的增大而增大;如果k<0,那么y随x的增大而减小.
及时练习
1、一次函数y=-5x+3中,y随x的_______而减小。
2、若一次函数y=ax-1中,y随x的增大而增大,则a_____.
设计意图:通过简单的练习,帮助学生加深对一次函数性质的理解与运用.
例题1:已知一次函数y=2x+1的图象上两点A(x1,y1)、B(x2,y2),且x1>x2,则y1____y2
变式:已知一次函数y=(m-1)x+1的图象上两点A(x1,y1)、B(x2,y2),且当x1>x2时,y1<y2,那么m的取值范围是______
设计意图:有了及时练习的基础,学生很容易理解例题1,变式是在例题1的基础上所做的改变.经过例1和变式,学生知道了题中的A、B两点具有一般代表性.这是对数学素养的提升.
观察与思考
给出两组自变量前面的系数不同的一次函数图像,每一组函数图像中的三条直线均互相平行,学生通过观察函数图像的位置关系以及函数表达式的特点,思考一次函数的表达式与图像位置关系之间的联系.
设计意图:在一次函数性质的学习中学生体会到了函数表达式对函数的性质有一定的内在联系,有了这样的意识,学生会比较容易将一次函数的表达式与图像特点联系起来.
归纳总结
直线的平行:直线y1=k1x+b1与直线y2=k2x+b2平行
k1=k2(b1≠b2)
通过以上的学习,学生知道了两个一次函数表达式中自变量前的系数可以决定这两个函数图像的位置关系,从而一个图像可以由另一个图像平移得到.如何平移,在没有进行引导的时候,学生的回答是可以把正比例函数上下平移得到另外两条直线(这是一种感性的认识).进一步引导学生将正比例函数上下平移多少个单位可以得到另外两个函数图像.
设计意图:学生在引导下会进一步思考平移多少个单位距离的问题.学生主要是通过图像与y轴的交点来回答的,虽然这是一个特殊点,但是通过这样的学习,可以让学生知道研究函数图像问题可以借助图像上的一点来研究,从而进一步提高了学生的数学素养.
归纳总结
直线的平移:直线y=kx+b可以看成是由直线y=kx通过平移得到,
(1)当b>0,沿着y轴向上平移
b
个单位;
(2)当b<0,沿着y轴向下平移|b|个单位.
例题2:已知直线y=ax+b与直线y=2x+1平行,且经过点(-3,
4),则a=____,
b=_____
变式:若一次函数的图象平行于直线y=2x,且与x轴交于点(-3,
0),则这个一次函数关系式为______________
设计意图:有了例2的铺垫,在解决变式的时候学生就知道要求一次函数关系式,可以先设一次函数关系式为y=kx+b,再根据条件分别求出k与b.
例题3:将一次函数y=-5x+1的图象沿y轴向下平移3个单位后的函数关系式为__________
变式:若一次函数y=-x-3是由某一次函数图象沿y轴向下平移4个单位得到的,则此一次函数关系式为_____________
延伸:直线y=-x+2向___平移_____个单位后刚好
经过点(-3,
-2)
设计意图:一次函数表达式中的常数项就是图像与y轴交点的纵坐标,再由之前的学习可以得到平移保持自变量系数不变,而常数项可以通过图像与纵坐标交点得到.从而强化了学生通过点来处理函数问题的意识.在得到了函数表达式后可以进一步引导学生求平移后的函数表达式可以直接对原一次函数表达式进行加减即可.而延伸题其实是个开放题,可以用熟悉的上下平移,也可以通过点来研究左右平移.
课堂小结
一次函数的性质:
一次函数y=kx+b中,
如果k>0,那么y随x的增大而增大;
如果k<0,那么y随x的增大而减小.
直线的平行:
若直线y1=k1x+b1与直线y2=k2x+b2平行,则k1=k2(b1≠b2)
直线的平移:直线y=kx+b可以看成是由直线y=kx通过平移得到,
(1)当b>0,沿着y轴向上平移
b
个单位;
(2)当b<0,沿着y轴向下平移|b|个单位.
一、教学目标
理解一次函数及其图像的相关性质
能熟练画出一次函数图像
进一步培养学生数形结合的意识和能力
经历一次函数及其图像有关性质的探究过程,培养学生探究、合作的能力
二、教学重点:一次函数图像的性质
三、教学难点:一次函数图像性质的探究
四、教学过程
观察与思考
观察第一组给定的三个一次函数的图像及对应的自变量与函数值的表格,思考此时y随x的增大在发生怎样的变化.再观察第二组一次函数的图像以及表格,思考同样的问题.
设计意图:通过图像的观察,让学生在感性中发现函数值随自变量的变化情况,再通过表格中的数据,让学生在理性中分析函数值随自变量的变化规律.在归纳总结中培养了学生语言表达能力以及分析问题的能力.
归纳总结
一次函数的性质:一次函数y=kx+b中,如果k>0,那么y随x的增大而增大;如果k<0,那么y随x的增大而减小.
及时练习
1、一次函数y=-5x+3中,y随x的_______而减小。
2、若一次函数y=ax-1中,y随x的增大而增大,则a_____.
设计意图:通过简单的练习,帮助学生加深对一次函数性质的理解与运用.
例题1:已知一次函数y=2x+1的图象上两点A(x1,y1)、B(x2,y2),且x1>x2,则y1____y2
变式:已知一次函数y=(m-1)x+1的图象上两点A(x1,y1)、B(x2,y2),且当x1>x2时,y1<y2,那么m的取值范围是______
设计意图:有了及时练习的基础,学生很容易理解例题1,变式是在例题1的基础上所做的改变.经过例1和变式,学生知道了题中的A、B两点具有一般代表性.这是对数学素养的提升.
观察与思考
给出两组自变量前面的系数不同的一次函数图像,每一组函数图像中的三条直线均互相平行,学生通过观察函数图像的位置关系以及函数表达式的特点,思考一次函数的表达式与图像位置关系之间的联系.
设计意图:在一次函数性质的学习中学生体会到了函数表达式对函数的性质有一定的内在联系,有了这样的意识,学生会比较容易将一次函数的表达式与图像特点联系起来.
归纳总结
直线的平行:直线y1=k1x+b1与直线y2=k2x+b2平行
k1=k2(b1≠b2)
通过以上的学习,学生知道了两个一次函数表达式中自变量前的系数可以决定这两个函数图像的位置关系,从而一个图像可以由另一个图像平移得到.如何平移,在没有进行引导的时候,学生的回答是可以把正比例函数上下平移得到另外两条直线(这是一种感性的认识).进一步引导学生将正比例函数上下平移多少个单位可以得到另外两个函数图像.
设计意图:学生在引导下会进一步思考平移多少个单位距离的问题.学生主要是通过图像与y轴的交点来回答的,虽然这是一个特殊点,但是通过这样的学习,可以让学生知道研究函数图像问题可以借助图像上的一点来研究,从而进一步提高了学生的数学素养.
归纳总结
直线的平移:直线y=kx+b可以看成是由直线y=kx通过平移得到,
(1)当b>0,沿着y轴向上平移
b
个单位;
(2)当b<0,沿着y轴向下平移|b|个单位.
例题2:已知直线y=ax+b与直线y=2x+1平行,且经过点(-3,
4),则a=____,
b=_____
变式:若一次函数的图象平行于直线y=2x,且与x轴交于点(-3,
0),则这个一次函数关系式为______________
设计意图:有了例2的铺垫,在解决变式的时候学生就知道要求一次函数关系式,可以先设一次函数关系式为y=kx+b,再根据条件分别求出k与b.
例题3:将一次函数y=-5x+1的图象沿y轴向下平移3个单位后的函数关系式为__________
变式:若一次函数y=-x-3是由某一次函数图象沿y轴向下平移4个单位得到的,则此一次函数关系式为_____________
延伸:直线y=-x+2向___平移_____个单位后刚好
经过点(-3,
-2)
设计意图:一次函数表达式中的常数项就是图像与y轴交点的纵坐标,再由之前的学习可以得到平移保持自变量系数不变,而常数项可以通过图像与纵坐标交点得到.从而强化了学生通过点来处理函数问题的意识.在得到了函数表达式后可以进一步引导学生求平移后的函数表达式可以直接对原一次函数表达式进行加减即可.而延伸题其实是个开放题,可以用熟悉的上下平移,也可以通过点来研究左右平移.
课堂小结
一次函数的性质:
一次函数y=kx+b中,
如果k>0,那么y随x的增大而增大;
如果k<0,那么y随x的增大而减小.
直线的平行:
若直线y1=k1x+b1与直线y2=k2x+b2平行,则k1=k2(b1≠b2)
直线的平移:直线y=kx+b可以看成是由直线y=kx通过平移得到,
(1)当b>0,沿着y轴向上平移
b
个单位;
(2)当b<0,沿着y轴向下平移|b|个单位.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
