人教版八年级上册数学第十二章全等三角形复习学案
文档属性
| 名称 | 人教版八年级上册数学第十二章全等三角形复习学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 142.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 19:33:21 | ||
图片预览


文档简介
教师
学生:
上课时间
年
月
日
阶段
基础(√
)
提高(
)
强化(
)
课时计划
共(
)次课、第(
)次课
教学课题
全等三角形
教学目标
1、掌握三角形全等的判定方法,利用三角形全等进行证明,掌握综合法证明的格式.
2强化知识及常考题型
教学
重点难点
教学重点:常见辅助线的作法及用三角形全等和角平分线的性质进行证明有关问题
教学难点:
灵活应用所学知识解决问题,精炼准确表达推理过程
教
学
过
程
见附件
教学反思
相信自己可以
伟大的梦想让成就随之成长,渺小的希望让你永落人群之后,相信自己,就必然会做到;一切都由意识掌控。如果自认高人一等,就一定出类拔萃,即使第一枚奖章还未颁发,你已获得难得的自信,你已懂得随梦想起飞。生命的战争并不总青睐于所谓的强者;或早或晚,赢得胜利的人,是相信是自己可以的人。
类型一:全等三角形的性质和判定
例题:
例1、两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:DC⊥BE
.
举一反三:如图,已知:AE⊥AB,AD⊥AC,AB=AC,∠B=∠C,求证:BD=CE.
类型二:常见辅助线的作法:
???
(1)在△ABC中,如AD是中线,常采用的作法是:
???
①延长AD到E,使DE=AD,连结BE(或过B作BE∥AC,交AD的延长线于E),如图甲。
???
②取AC的中点E,连结DE(或过D作DE∥BA,交AC于E),如图乙。
???
③延长BA至E,使AE=AB,连结CE(或过C作CE∥AD交BA的延长线于E),如图丙。
???
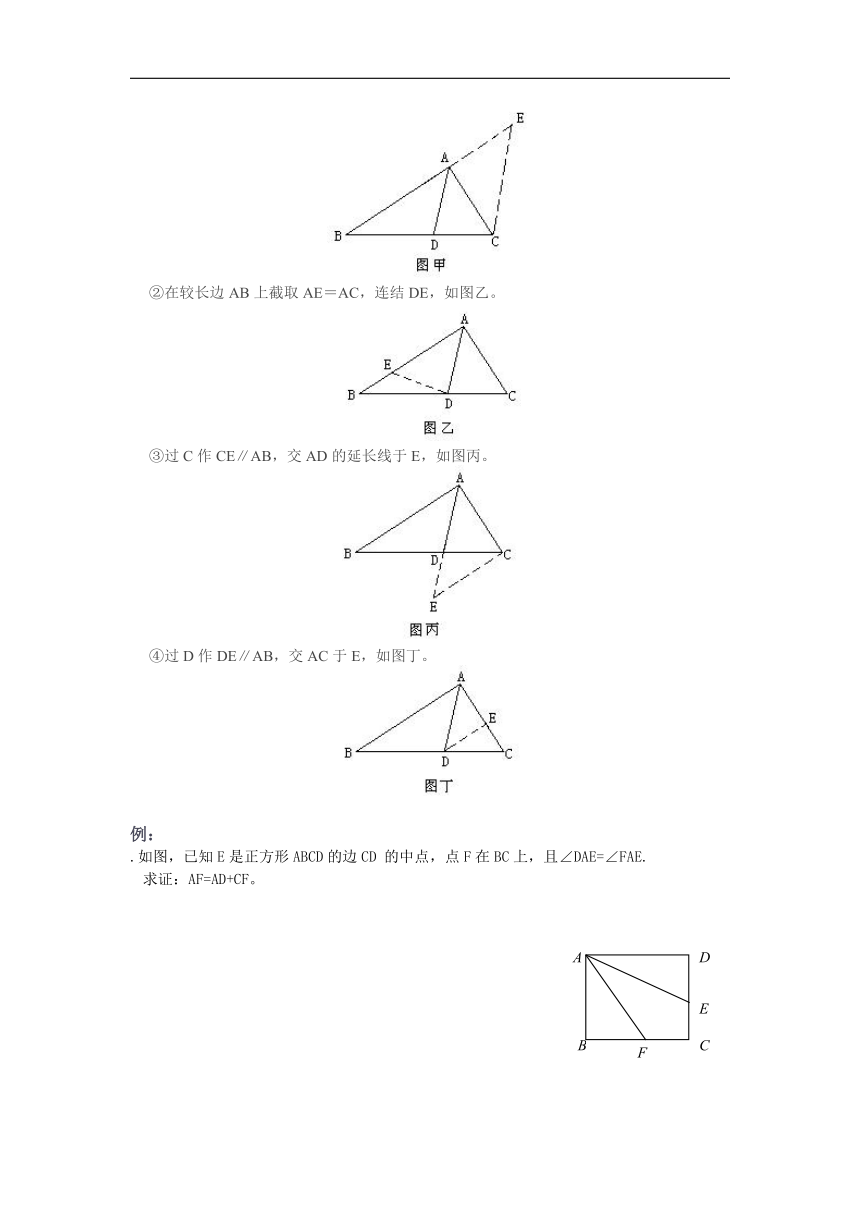
(2)在△ABC中,若AD是∠BAC的平分线,常采用的作法是:
???
①延长BA至E,使AE=AC,连结CE(或过C作CE∥AD,交BA的延长线于E),如图甲。
???
②在较长边AB上截取AE=AC,连结DE,如图乙。
???
③过C作CE∥AB,交AD的延长线于E,如图丙。
???
④过D作DE∥AB,交AC于E,如图丁。
例:
.如图,已知E是正方形ABCD的边CD
的中点,点F在BC上,且∠DAE=∠FAE.
求证:AF=AD+CF。
变式.
(8分)
如图所示,在△ABC中,∠C=90°,
AD是
∠BAC的平分线,DE⊥AB交AB于E,
F在AC上,BD=DF.
证明:(1)CF=EB.(2)AB=AF+2EB.
变式.如图,在△ABC中,∠B=60°,△ABC的角平分线AD,CE相交于点O.试说明AE+CD=AC..如图,在△ABC中,∠B=60°,△ABC的角平分线AD,CE相交于点O.试说明AE+CD=AC.
???
(3)在△ABC中,若D是AB的中点,常采用的作法是:
???
①过D作DE∥BC,交AC于E。
???
②取AC的中点E,连结DE。
???
③连结CD,用中线的性质。
???
④若已知△ABC为特殊三角形,可利用特殊三角形的性质:如为等腰三角形,考虑顶点平分线;若为直角三角形,考虑斜边中线;若为有一个角是30°的直角三角形,考虑斜边中线及30°角所对边之间的关系,常可作出中线。
?
(4)构造全等三角形法:
例,、在ΔABC中,AB>AC.求证:∠B<∠C
例.
已知:如图,AB∥CD,AD∥BC,证明:AB=DC,AD=BC
???
?例
如图,△ABC中,∠A=90°,AB=AC,BD平分∠ABC交AC于D,CE⊥BD的延长线于E,求证:BD=2CE。
???
分析:
和CE⊥BD”,想到延长CE、BA相交于F,因此先证明CF=2CE,再证明BD=CF。由此知需要证明△ABD≌△ACF。
综合题:
例.
(9分)如图所示,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.
求证:AF平分∠BAC.
例.
(9分)
已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图①),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点
H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.
14.已知:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE于D,CE⊥AE于E,(1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由;(2)当直线AE处于如图②的位置时,则BD,DE,CE的关系如何?请说明理由;(3)归纳(1)(2),请用简洁的语言表达BD,DE,CE之间的关系。
练习:
?
1.
如图1,已知△ABC是直角三角形,∠C=90°,∠A=60°,AB=8cm,CD是AB边上的高,则AD=___________,BD=___________。
图1
?
2
如图2,已知AB=AC=10cm,AB∥CD,CD⊥AD,若∠B=75°,则∠DAC=___________,AD=___________cm。
图2
3.
如图6,AD⊥AB,AE⊥AC,AD=AB,AE=AC,则下列各式中正确的是(???
)
图6
???
A.
△ABD≌△ACE??????????????????????????
B.
△ADF≌△AEG
???
C.
△BMF≌△CMG?????????????????????????
D.
△ADC≌△ABE
?
4已知:在△ABC中,AD是BC边上的高,AB=AC,∠BAC=120°,DE⊥AB于E,DF⊥AC于F。
???
求证:。
5如图7,在△ABC中,∠BAC=90°,D是△ABC内一点,将△ADB绕A点旋转至△AD'C,△AD'C与△ADB能完全重合,求∠DAD'的度数。
图7
6,:如图8△ABC是边长为1的等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,点M、N分别在AB、AC上,且∠MDN=60°
???
求证:△AMN的周长l=2
学生:
上课时间
年
月
日
阶段
基础(√
)
提高(
)
强化(
)
课时计划
共(
)次课、第(
)次课
教学课题
全等三角形
教学目标
1、掌握三角形全等的判定方法,利用三角形全等进行证明,掌握综合法证明的格式.
2强化知识及常考题型
教学
重点难点
教学重点:常见辅助线的作法及用三角形全等和角平分线的性质进行证明有关问题
教学难点:
灵活应用所学知识解决问题,精炼准确表达推理过程
教
学
过
程
见附件
教学反思
相信自己可以
伟大的梦想让成就随之成长,渺小的希望让你永落人群之后,相信自己,就必然会做到;一切都由意识掌控。如果自认高人一等,就一定出类拔萃,即使第一枚奖章还未颁发,你已获得难得的自信,你已懂得随梦想起飞。生命的战争并不总青睐于所谓的强者;或早或晚,赢得胜利的人,是相信是自己可以的人。
类型一:全等三角形的性质和判定
例题:
例1、两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:DC⊥BE
.
举一反三:如图,已知:AE⊥AB,AD⊥AC,AB=AC,∠B=∠C,求证:BD=CE.
类型二:常见辅助线的作法:
???
(1)在△ABC中,如AD是中线,常采用的作法是:
???
①延长AD到E,使DE=AD,连结BE(或过B作BE∥AC,交AD的延长线于E),如图甲。
???
②取AC的中点E,连结DE(或过D作DE∥BA,交AC于E),如图乙。
???
③延长BA至E,使AE=AB,连结CE(或过C作CE∥AD交BA的延长线于E),如图丙。
???
(2)在△ABC中,若AD是∠BAC的平分线,常采用的作法是:
???
①延长BA至E,使AE=AC,连结CE(或过C作CE∥AD,交BA的延长线于E),如图甲。
???
②在较长边AB上截取AE=AC,连结DE,如图乙。
???
③过C作CE∥AB,交AD的延长线于E,如图丙。
???
④过D作DE∥AB,交AC于E,如图丁。
例:
.如图,已知E是正方形ABCD的边CD
的中点,点F在BC上,且∠DAE=∠FAE.
求证:AF=AD+CF。
变式.
(8分)
如图所示,在△ABC中,∠C=90°,
AD是
∠BAC的平分线,DE⊥AB交AB于E,
F在AC上,BD=DF.
证明:(1)CF=EB.(2)AB=AF+2EB.
变式.如图,在△ABC中,∠B=60°,△ABC的角平分线AD,CE相交于点O.试说明AE+CD=AC..如图,在△ABC中,∠B=60°,△ABC的角平分线AD,CE相交于点O.试说明AE+CD=AC.
???
(3)在△ABC中,若D是AB的中点,常采用的作法是:
???
①过D作DE∥BC,交AC于E。
???
②取AC的中点E,连结DE。
???
③连结CD,用中线的性质。
???
④若已知△ABC为特殊三角形,可利用特殊三角形的性质:如为等腰三角形,考虑顶点平分线;若为直角三角形,考虑斜边中线;若为有一个角是30°的直角三角形,考虑斜边中线及30°角所对边之间的关系,常可作出中线。
?
(4)构造全等三角形法:
例,、在ΔABC中,AB>AC.求证:∠B<∠C
例.
已知:如图,AB∥CD,AD∥BC,证明:AB=DC,AD=BC
???
?例
如图,△ABC中,∠A=90°,AB=AC,BD平分∠ABC交AC于D,CE⊥BD的延长线于E,求证:BD=2CE。
???
分析:
和CE⊥BD”,想到延长CE、BA相交于F,因此先证明CF=2CE,再证明BD=CF。由此知需要证明△ABD≌△ACF。
综合题:
例.
(9分)如图所示,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.
求证:AF平分∠BAC.
例.
(9分)
已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图①),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点
H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.
14.已知:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE于D,CE⊥AE于E,(1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由;(2)当直线AE处于如图②的位置时,则BD,DE,CE的关系如何?请说明理由;(3)归纳(1)(2),请用简洁的语言表达BD,DE,CE之间的关系。
练习:
?
1.
如图1,已知△ABC是直角三角形,∠C=90°,∠A=60°,AB=8cm,CD是AB边上的高,则AD=___________,BD=___________。
图1
?
2
如图2,已知AB=AC=10cm,AB∥CD,CD⊥AD,若∠B=75°,则∠DAC=___________,AD=___________cm。
图2
3.
如图6,AD⊥AB,AE⊥AC,AD=AB,AE=AC,则下列各式中正确的是(???
)
图6
???
A.
△ABD≌△ACE??????????????????????????
B.
△ADF≌△AEG
???
C.
△BMF≌△CMG?????????????????????????
D.
△ADC≌△ABE
?
4已知:在△ABC中,AD是BC边上的高,AB=AC,∠BAC=120°,DE⊥AB于E,DF⊥AC于F。
???
求证:。
5如图7,在△ABC中,∠BAC=90°,D是△ABC内一点,将△ADB绕A点旋转至△AD'C,△AD'C与△ADB能完全重合,求∠DAD'的度数。
图7
6,:如图8△ABC是边长为1的等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,点M、N分别在AB、AC上,且∠MDN=60°
???
求证:△AMN的周长l=2
