人教版八年级上册数学第十一章三角形的复习学案
文档属性
| 名称 | 人教版八年级上册数学第十一章三角形的复习学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 00:00:00 | ||
图片预览



文档简介
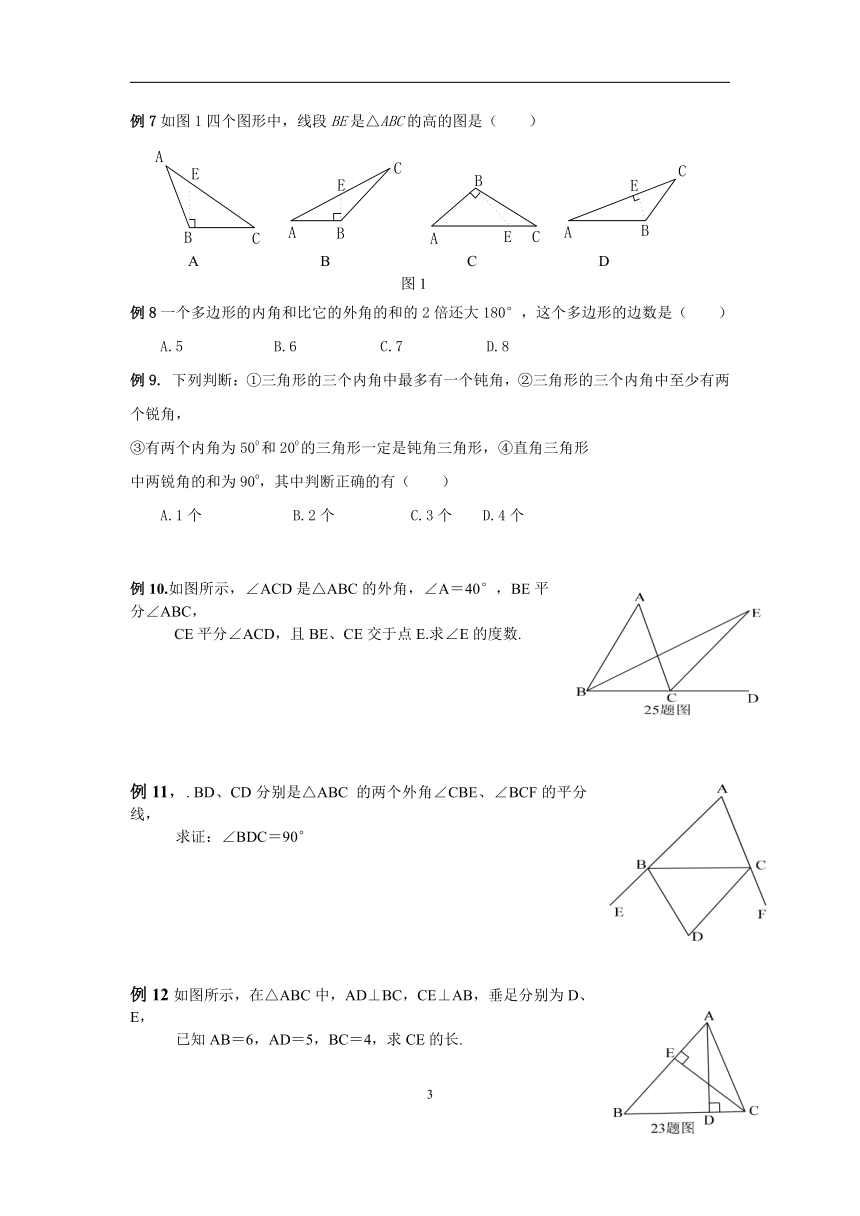
三角形复习教案
本章知识点
1、三角形的定义:由不在同一直线上的
条线段
连接所组成的图形
2、三角形的表示方法:三角形ABC可表示为:
;
3、三角形的有关元素:
(1)ΔABC的顶点分别为A、
、
;
(2)ΔABC的内角分别为∠ABC,
,
;
(3)ΔABC的三条边分别为AB,
,
;或,
、
;
(4)顶点A的对边是
,顶点B的对边分别是
,顶点C的对边分别是
。
4、三角形的分类:
锐角三角形
①按角分类
不等边三角形:
三角形三条边
②
按边分类
底边和腰不
的等腰三角形
等腰三角形
(有两条边相等)
等边三角形:三条边都
5、三角形三边的关系:
⑴、三角形的任意两边之和
第三边;
⑵、三角形的任意两边之差
第三边。
6、几何语言表示三角形的高、中线、解平分线;
(1)三角形的中线(如图一):
∵CF是AB上的中线
∴①AF
=
=
②AB=2
=2
(2)三角形的角平分线(如图二):
∵BE是ΔABC中∠ABC的角平分线
∴①∠1=∠2=
∠ABC
②∠ABC=2∠
=2∠
(3)三角形的高线(如图三):
∵AD为ΔABC中BC边上的高,
∴①
⊥
②∠
=∠
=90°
7、三角形内角和定理:三角形的三个内角和等于
。
8、三角形的外角:
(1)三角形的外角的定义:三角形的
与
组成的角叫做三角形的外角。
(2)三角形外角的性质:
①三角形的一个外角与它相邻的内角
;
②三角形的一个外角
与它不相邻的两个内角的和;
③三角形的一个外角
任何一个与它不相邻的内角。
(3)三角形的外角和等于
。
9、多边形:
(1)多边形的定义:在平面内,由一些不在同一条直线上的线段
组成的图形叫做多边形。
(2)多边形的对角线:连接多边形
两个顶点的线段。
(3)从n边形的一个顶点出发,可以引 条对角线,一共可以引
对角线。
(4)从n边形的一个顶点出发,可以引 条对角线,它将n边形分成 个三角形.
(5)正多边形的定义:在平面内,各个
都相等,各条
也都相等的多边形叫做正多边形。
10、n边形的内角和定理:n边形的内角和等于
。
11、n边形的外角和定理:n边形的外角和等于
。
12、正n边形的每个内角等于
;正n边形的每个外角等于
。
经典例题:
有下列长度的三条线段,能组成三角形的是( )
A
2cm,3cm,4cm B
1cm,4cm,2cm
C1cm,2cm,3cm
D
6cm,2cm,3cm
例2.
六边形的对角线的条数是(
)
(A)7
(B)8
(C)9
(D)10
例3.右图中三角形的个数是(
)
A.6
B.7
C.8
D.9
例4.能把一个任意三角形分成面积相等的两部分是( )
A.角平分线 B.中线 C.高 D.A、B、C都可以
例5下列不能够镶嵌的正多边形组合是( )
A.正三角形与正六边形
B.正方形与正六边形
C.正三角形与正方形
D.正五边形与正十边形
例6.一个三角形三个内角的度数之比为,这个三角形一定是(
)
A.直角三角形
B.等腰三角形
C.锐角三角形
D.钝角三角形
.
变式:
三角形的一个外角是锐角,则此三角形的形状是(
)
A.锐角三角形
B.钝角三角形
C.直角三角形
D.无
例7如图1四个图形中,线段BE是△ABC的高的图是( )
例8一个多边形的内角和比它的外角的和的2倍还大180°,这个多边形的边数是(
)
A.5
B.6
C.7
D.8
例9.
下列判断:①三角形的三个内角中最多有一个钝角,②三角形的三个内角中至少有两个锐角,
③有两个内角为500和200的三角形一定是钝角三角形,④直角三角形
中两锐角的和为900,其中判断正确的有( )
A.1个
B.2个
C.3个
D.4个
例10.如图所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,
CE平分∠ACD,且BE、CE交于点E.求∠E的度数.
例11,.
BD、CD分别是△ABC
的两个外角∠CBE、∠BCF的平分线,
求证:∠BDC=90°
例12如图所示,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,
已知AB=6,AD=5,BC=4,求CE的长.
例13.在一次班会上,班主任给6位同学过生日,买了一块三角形的蛋糕,平均分给这六位同学,要求只切三刀,你有办法达到要求吗?试把你的方案画出来.并说明理由.
例14.(本小题5分)一个零件的形状如图所示,零件要求∠A必须等于90°,∠B和∠C分别为45°和35°,检验工人量得∠BDC=159°,就断定这个零件不合格,你知道为什么吗?
【解题方案】可由∠C,∠B,∠A求∠BDC≠159°,则零件就不合格.
例15如图5,四边形ABCD中,∠A=∠C=90°,BE、CF分别是∠B、∠D的平分线.
(1)∠1与∠2有何关系,为什么?
(2)BE与DF有何关系?请说明理由.
例16.如图22(1)所示,称“对顶三角形”,其中,∠A+∠B=∠C+∠D,
利用这个结论,完成下列填空.
如图22题(2),∠A+∠B+∠C+∠D+∠E=
.
如图22题(3),∠A+∠B+∠C+∠D+∠E=
.
如图22题(4),∠1+∠2+∠3+∠4+∠5+∠6=
.
如图22题(5),∠1+∠2+∠3+∠4+∠5+∠6+∠7=
.
练习:
1、以下列长度(cm)的三条小木棒,若首尾顺次连接,能钉成三角形的是(
)。
(A)10、14、24
(B)12、16、32
(C)16、6、4
(D)8、10、12
2、下面各角能成为某多边形的内角和的是( )
A.430°
B.4343°
C.4320°
D.4360°
3、一个多边形的内角和比它的外角的和的2倍还大180°,这个多边形的边数是(
)
A.5
B.6
C.7
D.8
4、在下列条件中:①∠A+∠B=∠C,②∠A∶∠B∶∠C=1∶2∶3,③∠A=90°-∠B,④∠A=∠B-∠C中,能确定△ABC是直角三角形的条件有( ).
A.1个
B.2个
C.3个
D.4个
5、一个角的两边分别垂直于另一个角的两边,那么这两个角之间的关系是( ).
A.相等
B.互补
C.相等或互补
D.无法确
6、如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( ).
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2)
7、五角星的顶点为A、B、C、D、E,∠A
+∠B
+∠C
+∠D
+∠E
的度数为(
)
A、90°
B、180°
C、270°
D、360°
8、如图,将一副三角板叠放在一起,使直角的顶点重合
于O,则∠AOC+∠DOB=(
)
A、900
B、1200
C、1600
D、1800
9、一个多边形的内角和是外角和的2倍,则这个多边形的边数为(
)
A、4
B、5
C、6
D、7
10、过多边形的一个顶点的所有对角线把多边形分成8个三角形,这个多边形
的边数是(
)
A、8
B、9
C、10
D、11
(二)填空题:
1、已知等腰三角形两边长是4cm和7cm,则它的周长是
。
2已知等腰三角形的一个内角是50°,则它的另外两个内角是
。
3、如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,
DF⊥CE,则∠CDF=________度
4、一个多边形的每一个外角都等于30°,这个多边形的边数是
_________________,它的内角和是__________度。
5,为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样
做的道理是
。
,6,、若三角形三个内角度数的比为2:3:4,则相应的外角比
是
.
,7、如图ABC中,AD是BC上的中线,BE是ABD中AD边上的中线,若ABC
的面积是24,则ABE的面积是________。
8.三角形的三边长分别为5,1+2x,8,则x的取值范围是________.
9,若一个等腰三角形的两边长分别是3
cm和5
cm,则它的周长是
cm。
10,一些大小、形状完全相同的三角形----------密铺地板,正五边形-----------密铺地板.
(三)解答题:
1、已知一个三角形的三边长分别是4,2a
–
3
,5,其中a是奇数,求a的值。
2、如图,在⊿ABC中,∠B
=
50?,∠C
=
70?,AD是高,AE是角平分线,
求∠EAD的度数。
3、如图,AD是⊿ABC的外角平分线,交BC的延长线于D点,若∠B
=
30?,∠DAE
=
55?,求∠ACD的度数。
4、如图,经测量,B处在A处的南偏西57°的方向,C处在A处的南偏东15°方向,C处在B处的北偏东82°方向,求∠C的度数.
5.
如图,DE∥BC,∠ADE=∠EFC,那么∠1与∠2相等吗?说明理由。
5.
如图,长方形OABC中,O为平面直角坐标系的原点,A、C两点的坐标分别为(3,0),(0,5),点B在第一象限内。
(1)如图1,写出点B的坐标(
);
(2)如图2,若过点C的直线CD交AB于点D,且把长方形OABC的周长分为3:1两部分,求点D的坐标(
);
(3)如图3,将(2)中的线段CD向下平移2个单位,得到C/D/,试计算四边形OAD/C/的面积
.
8
本章知识点
1、三角形的定义:由不在同一直线上的
条线段
连接所组成的图形
2、三角形的表示方法:三角形ABC可表示为:
;
3、三角形的有关元素:
(1)ΔABC的顶点分别为A、
、
;
(2)ΔABC的内角分别为∠ABC,
,
;
(3)ΔABC的三条边分别为AB,
,
;或,
、
;
(4)顶点A的对边是
,顶点B的对边分别是
,顶点C的对边分别是
。
4、三角形的分类:
锐角三角形
①按角分类
不等边三角形:
三角形三条边
②
按边分类
底边和腰不
的等腰三角形
等腰三角形
(有两条边相等)
等边三角形:三条边都
5、三角形三边的关系:
⑴、三角形的任意两边之和
第三边;
⑵、三角形的任意两边之差
第三边。
6、几何语言表示三角形的高、中线、解平分线;
(1)三角形的中线(如图一):
∵CF是AB上的中线
∴①AF
=
=
②AB=2
=2
(2)三角形的角平分线(如图二):
∵BE是ΔABC中∠ABC的角平分线
∴①∠1=∠2=
∠ABC
②∠ABC=2∠
=2∠
(3)三角形的高线(如图三):
∵AD为ΔABC中BC边上的高,
∴①
⊥
②∠
=∠
=90°
7、三角形内角和定理:三角形的三个内角和等于
。
8、三角形的外角:
(1)三角形的外角的定义:三角形的
与
组成的角叫做三角形的外角。
(2)三角形外角的性质:
①三角形的一个外角与它相邻的内角
;
②三角形的一个外角
与它不相邻的两个内角的和;
③三角形的一个外角
任何一个与它不相邻的内角。
(3)三角形的外角和等于
。
9、多边形:
(1)多边形的定义:在平面内,由一些不在同一条直线上的线段
组成的图形叫做多边形。
(2)多边形的对角线:连接多边形
两个顶点的线段。
(3)从n边形的一个顶点出发,可以引 条对角线,一共可以引
对角线。
(4)从n边形的一个顶点出发,可以引 条对角线,它将n边形分成 个三角形.
(5)正多边形的定义:在平面内,各个
都相等,各条
也都相等的多边形叫做正多边形。
10、n边形的内角和定理:n边形的内角和等于
。
11、n边形的外角和定理:n边形的外角和等于
。
12、正n边形的每个内角等于
;正n边形的每个外角等于
。
经典例题:
有下列长度的三条线段,能组成三角形的是( )
A
2cm,3cm,4cm B
1cm,4cm,2cm
C1cm,2cm,3cm
D
6cm,2cm,3cm
例2.
六边形的对角线的条数是(
)
(A)7
(B)8
(C)9
(D)10
例3.右图中三角形的个数是(
)
A.6
B.7
C.8
D.9
例4.能把一个任意三角形分成面积相等的两部分是( )
A.角平分线 B.中线 C.高 D.A、B、C都可以
例5下列不能够镶嵌的正多边形组合是( )
A.正三角形与正六边形
B.正方形与正六边形
C.正三角形与正方形
D.正五边形与正十边形
例6.一个三角形三个内角的度数之比为,这个三角形一定是(
)
A.直角三角形
B.等腰三角形
C.锐角三角形
D.钝角三角形
.
变式:
三角形的一个外角是锐角,则此三角形的形状是(
)
A.锐角三角形
B.钝角三角形
C.直角三角形
D.无
例7如图1四个图形中,线段BE是△ABC的高的图是( )
例8一个多边形的内角和比它的外角的和的2倍还大180°,这个多边形的边数是(
)
A.5
B.6
C.7
D.8
例9.
下列判断:①三角形的三个内角中最多有一个钝角,②三角形的三个内角中至少有两个锐角,
③有两个内角为500和200的三角形一定是钝角三角形,④直角三角形
中两锐角的和为900,其中判断正确的有( )
A.1个
B.2个
C.3个
D.4个
例10.如图所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,
CE平分∠ACD,且BE、CE交于点E.求∠E的度数.
例11,.
BD、CD分别是△ABC
的两个外角∠CBE、∠BCF的平分线,
求证:∠BDC=90°
例12如图所示,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,
已知AB=6,AD=5,BC=4,求CE的长.
例13.在一次班会上,班主任给6位同学过生日,买了一块三角形的蛋糕,平均分给这六位同学,要求只切三刀,你有办法达到要求吗?试把你的方案画出来.并说明理由.
例14.(本小题5分)一个零件的形状如图所示,零件要求∠A必须等于90°,∠B和∠C分别为45°和35°,检验工人量得∠BDC=159°,就断定这个零件不合格,你知道为什么吗?
【解题方案】可由∠C,∠B,∠A求∠BDC≠159°,则零件就不合格.
例15如图5,四边形ABCD中,∠A=∠C=90°,BE、CF分别是∠B、∠D的平分线.
(1)∠1与∠2有何关系,为什么?
(2)BE与DF有何关系?请说明理由.
例16.如图22(1)所示,称“对顶三角形”,其中,∠A+∠B=∠C+∠D,
利用这个结论,完成下列填空.
如图22题(2),∠A+∠B+∠C+∠D+∠E=
.
如图22题(3),∠A+∠B+∠C+∠D+∠E=
.
如图22题(4),∠1+∠2+∠3+∠4+∠5+∠6=
.
如图22题(5),∠1+∠2+∠3+∠4+∠5+∠6+∠7=
.
练习:
1、以下列长度(cm)的三条小木棒,若首尾顺次连接,能钉成三角形的是(
)。
(A)10、14、24
(B)12、16、32
(C)16、6、4
(D)8、10、12
2、下面各角能成为某多边形的内角和的是( )
A.430°
B.4343°
C.4320°
D.4360°
3、一个多边形的内角和比它的外角的和的2倍还大180°,这个多边形的边数是(
)
A.5
B.6
C.7
D.8
4、在下列条件中:①∠A+∠B=∠C,②∠A∶∠B∶∠C=1∶2∶3,③∠A=90°-∠B,④∠A=∠B-∠C中,能确定△ABC是直角三角形的条件有( ).
A.1个
B.2个
C.3个
D.4个
5、一个角的两边分别垂直于另一个角的两边,那么这两个角之间的关系是( ).
A.相等
B.互补
C.相等或互补
D.无法确
6、如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( ).
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2)
7、五角星的顶点为A、B、C、D、E,∠A
+∠B
+∠C
+∠D
+∠E
的度数为(
)
A、90°
B、180°
C、270°
D、360°
8、如图,将一副三角板叠放在一起,使直角的顶点重合
于O,则∠AOC+∠DOB=(
)
A、900
B、1200
C、1600
D、1800
9、一个多边形的内角和是外角和的2倍,则这个多边形的边数为(
)
A、4
B、5
C、6
D、7
10、过多边形的一个顶点的所有对角线把多边形分成8个三角形,这个多边形
的边数是(
)
A、8
B、9
C、10
D、11
(二)填空题:
1、已知等腰三角形两边长是4cm和7cm,则它的周长是
。
2已知等腰三角形的一个内角是50°,则它的另外两个内角是
。
3、如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,
DF⊥CE,则∠CDF=________度
4、一个多边形的每一个外角都等于30°,这个多边形的边数是
_________________,它的内角和是__________度。
5,为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样
做的道理是
。
,6,、若三角形三个内角度数的比为2:3:4,则相应的外角比
是
.
,7、如图ABC中,AD是BC上的中线,BE是ABD中AD边上的中线,若ABC
的面积是24,则ABE的面积是________。
8.三角形的三边长分别为5,1+2x,8,则x的取值范围是________.
9,若一个等腰三角形的两边长分别是3
cm和5
cm,则它的周长是
cm。
10,一些大小、形状完全相同的三角形----------密铺地板,正五边形-----------密铺地板.
(三)解答题:
1、已知一个三角形的三边长分别是4,2a
–
3
,5,其中a是奇数,求a的值。
2、如图,在⊿ABC中,∠B
=
50?,∠C
=
70?,AD是高,AE是角平分线,
求∠EAD的度数。
3、如图,AD是⊿ABC的外角平分线,交BC的延长线于D点,若∠B
=
30?,∠DAE
=
55?,求∠ACD的度数。
4、如图,经测量,B处在A处的南偏西57°的方向,C处在A处的南偏东15°方向,C处在B处的北偏东82°方向,求∠C的度数.
5.
如图,DE∥BC,∠ADE=∠EFC,那么∠1与∠2相等吗?说明理由。
5.
如图,长方形OABC中,O为平面直角坐标系的原点,A、C两点的坐标分别为(3,0),(0,5),点B在第一象限内。
(1)如图1,写出点B的坐标(
);
(2)如图2,若过点C的直线CD交AB于点D,且把长方形OABC的周长分为3:1两部分,求点D的坐标(
);
(3)如图3,将(2)中的线段CD向下平移2个单位,得到C/D/,试计算四边形OAD/C/的面积
.
8
