人教版九年级数学下册导学案 27.3 第2课时 平面直角坐标系中的位似
文档属性
| 名称 | 人教版九年级数学下册导学案 27.3 第2课时 平面直角坐标系中的位似 |  | |
| 格式 | zip | ||
| 文件大小 | 444.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 21:17:38 | ||
图片预览



文档简介
27.3
位
似
第2课时
平面直角坐标系中的位似
学习目标:1.
理解平面直角坐标系中,位似图形对应点的坐标之间的联系.
2.
会用图形的坐标的变化表示图形的位似变换,掌握把一个图形按一定比例放大或缩小后,点的坐标变化的规律.
(重点、难点)
3.
了解四种图形变换
(平移、轴对称、旋转和位似)
的异同,并能在复杂图形中找出这些变换.
【自主学习】
一、知识链接
1.
两个相似多边形,如果它们对应顶点所在的直线相交于一点,我们就把这样的两个图形叫做
,这个交点叫做
.位似图形上任意一对对应点到位似中心的距离之比等于
,
对应线段
.
2.
如何判断两个图形是不是位似图形?
3.
画位似图形的一般步骤有哪些?
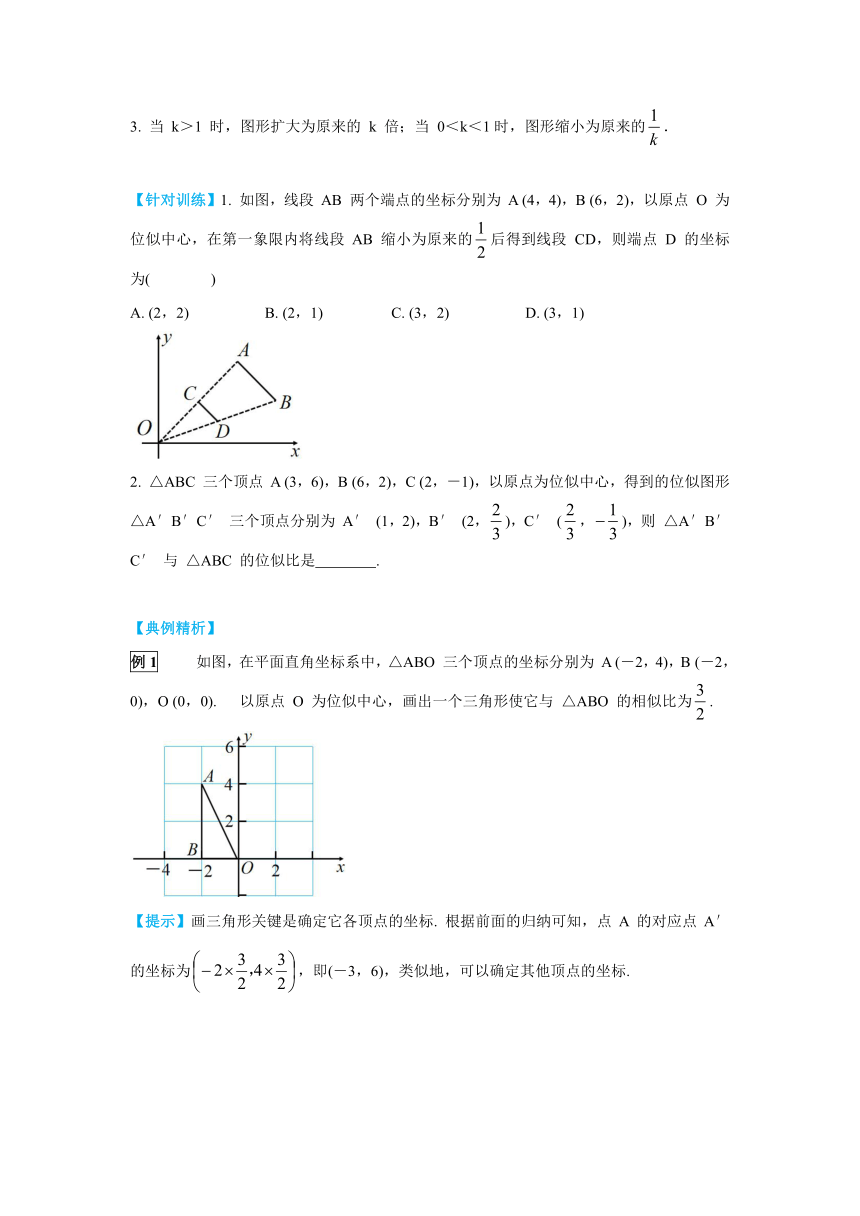
4.
位似的基本模型:
【合作探究】
要点探究
探究点1:平面直角坐标系中的位似变换
观察1
在平面直角坐标系中,有两点
A
(6,3),B
(6,0).以原点
O
为位似中心,相似比为,把线段
AB
缩小,观察对应点之间坐标的变化.
回答1
如图,把
AB
缩小后
A,B
的对应点为
A′
(
,
),
B'
(
,
);A"
(
,
),B"
(
,
).
观察1
△AOC
三个顶点坐标分别为
A
(4,4),O
(0,0),C
(5,0),以点
O
为位似中心,相似比为
2,将△AOC
放大,观察对应顶点坐标的变化.
回答2
如图,把
△AOC
放大后
A,O,C
的对应点为
A'
(
,
),C'
(
,
);A"
(
,
),C"
(
,
).
思考
1.在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?
2.所作位似图形与原图形在原点的同侧,那么对应顶点的坐标的比与其相似比是何关系?如果所作位似图形与原图形在原点的异侧呢?
【要点归纳】1.
在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可作两个.
2.
当位似图形在原点同侧时,其对应顶点的坐标的比为
k;当位似图形在原点两侧时,其对应顶点的坐标的比为-k.(位似中的相似比k一般指新图形与原图形的比)
3.
当
k>1
时,图形扩大为原来的
k
倍;当
0<k<1时,图形缩小为原来的.
【针对训练】1.
如图,线段
AB
两个端点的坐标分别为
A
(4,4),B
(6,2),以原点
O
为位似中心,在第一象限内将线段
AB
缩小为原来的后得到线段
CD,则端点
D
的坐标为(
)
A.
(2,2)
B.
(2,1)
C.
(3,2)
D.
(3,1)
2.
△ABC
三个顶点
A
(3,6),B
(6,2),C
(2,-1),以原点为位似中心,得到的位似图形
△A′B′C′
三个顶点分别为
A′
(1,2),B′
(2,),C′
(,),则
△A′B′C′
与
△ABC
的位似比是
.
【典例精析】
例1
如图,在平面直角坐标系中,△ABO
三个顶点的坐标分别为
A
(-2,4),B
(-2,0),O
(0,0).
以原点
O
为位似中心,画出一个三角形使它与
△ABO
的相似比为.
【提示】画三角形关键是确定它各顶点的坐标.
根据前面的归纳可知,点
A
的对应点
A′
的坐标为,即(-3,6),类似地,可以确定其他顶点的坐标.
【针对训练】在平面直角坐标系中,四边形
OABC
的顶点坐标分别为
O
(0,0),A
(6,0),B
(3,6),C
(-3,3).
以原点
O
为位似中心,画出四边形
OABC
的位似图形,使它与四边形
OABC
的相似是
2
:
3.
探究点2:平面直角坐标系中的图形变换
思考
至此,我们已经学习了四种变换:平移、轴对称、旋转和位似,你能说出它们之间的异同吗?在如图所示的图案中,你能找到这些变换吗?
【针对训练】将图中的
△ABC
做下列变换,画出相应的图形,指出三个顶点的坐标所发生的变化.(每个小方格的长度为1个单位长度)
(1)
沿
y
轴正向平移
3
个单位长度;
(2)
关于
x
轴对称;
(3)
在点C的左侧,以
点C
为位似中心,将△ABC
放大为原来的2倍;
(4)
以
C
为中心,将△ABC
顺时针旋转180°.
二、课堂小结
【达标练习】
1.
将平面直角坐标系中某个图形的各点坐标做如下变化,其中属于位似变换的是(
)
A.
将各点的纵坐标乘以
2,横坐标不变
B.
将各点的横坐标除以
2,纵坐标不变
C.
将各点的横坐标、纵坐标都乘以
2
D.
将各点的纵坐标减去
2,横坐标加上
2
2.
如图,小朋在坐标系中以A为位似中心画了两个位似的直角三角形,可不小心把
E
点弄脏了,则
E
点坐标为
(
)
A.(4,-3)
B.(4,-2)
C.(4,-4)
D.(4,-6)
第2题图
第3题图
3.
如图,某学习小组在讨论
“变化的鱼”时,知道大鱼与小鱼是位似图形,则小鱼上的点
(a,b)
对应大鱼上的点
.
4.
原点
O
是
△ABC
和
△A′B′C′
的位似中心,点
A
(1,0)
与点
A′
(-2,0)
是对应点,△ABC
的面积是,则
△A′B′C′的面积是
.
5.
△ABC
三个顶点坐标分别为
A
(2,-2),B
(4,-5),C
(5,-2),以原点
O
为位似中心,将这个三角形放大为原来的
2
倍.
6.
在
13×13
的网格图中,已知
△ABC
和点
M
(1,2).
(1)
以点
M
为位似中心,位似比为
2,画出
△ABC的位似图形
△A′B′C′;
(2)
写出
△A′B′C′
的各顶点坐标.
7.
如图,点
A
的坐标为
(3,4),点
O
的坐标为
(0,0),点
B
的坐标为
(4,0).
(1)
将
△AOB
沿
x
轴向左平移1
个单位长度后得△A1O1B1,则点
A1
的坐标为
,△A1O1B1的面积为
;
(2)
将
△AOB
绕原点旋转
180°后得
△A2O2B2,则点
A2
的坐标为
;
(3)
将
△AOB
沿
x
轴翻折后得
△A3O3B3,则点
A3
的坐标为
;
(4)
以
O
为位似中心,按比例尺
1
:
2
将
△AOB
放大后得
△A4O4B4,若点
B4
在
x
轴负半轴上,则点
A4的坐标为
,△A4O4B4的面积为
.
拓展提升:
8.
如图,正方形
ABCD
和正方形
OEFG
中,点
A
和点
F
的坐标分别为
(3,2),(-1,-1),则两个正方形的位似中心的坐标是
.
【分析】此时两个正方形位似,但未指明对应的点,因此需要分类讨论
参考答案
自主学习
一、知识链接
1.
位似图形
位似中心
相似比
平行或在同一条直线上
2.
解:看它的对应点的连线是否交于一点
3.
解:过位似中心与其他各个顶点各作一条直线,按位似比在直线截取对应长度的线段,依次连接.
合作探究
一、要点探究
探究点1:平面直角坐标系中的位似变换
回答1
2
1
2
0
-2
-1
-2
0
回答2
8
8
10
0
-8
-8
-10
0
【针对训练】1.
D
2.1:3
【典例精析】
例1
解:利用位似中对应点的坐标的变化规律,分别取点
A′
(-3,6),B′
(-3,0),O
(0,0).顺次连接点
A′
,B′
,O,所得的
△A′
B′
O
就是要画的一个图形.
【针对训练】解:画法一:将四边形
OABC
各顶点的坐标都乘;在平面直角坐标系中描点O
(0,0),A'
(4,0),B'
(2,4),C′
(-2,2),用线段顺次连接O,A',B',C'.
画法二:将四边形
OABC
各顶点的坐标都乘;在平面直角坐标系中描点O
(0,0),
A″
(-4,0),B″
(-2,-4),C″
(2,-2),用线段顺次连接O,A″,B″,C″.
探究点2:平面直角坐标系中的图形变换
【针对训练】解:(1)如图中红色三角形,横坐标不变,纵坐标加3;
(2)如图中蓝色三角形,纵坐标互为相反数;
(3)如图中粉色三角形,C不变,A横纵坐标均为-2,B的横坐标-1,纵坐标+1.
(4)如图中绿色三角形,C不变,A的横纵坐标均加4,B的横坐标加2,纵坐标-2.
当堂检测
1.
C
2.
A
3.
(-2a,-2b)
4.
6
5.
解:点的坐标为A'
(4,-4),B'
(8,-10),C'
(10,-4);A″
(-4,4),B″
(-8,10),C″
(-10,4).
6.
解:(1)如图所示.
(2)△A′B′C′
的各顶点坐标分别为
A′
(3,6),B′
(5,2),C′
(11,4).
7.
(1)
(2,4)
8
(2)
(-4,-3)
(3)
(3,-4)
(4)
(-6,-8)
32
拓展提升:
8.
(1,0)
或
(-5,-2)
位
似
第2课时
平面直角坐标系中的位似
学习目标:1.
理解平面直角坐标系中,位似图形对应点的坐标之间的联系.
2.
会用图形的坐标的变化表示图形的位似变换,掌握把一个图形按一定比例放大或缩小后,点的坐标变化的规律.
(重点、难点)
3.
了解四种图形变换
(平移、轴对称、旋转和位似)
的异同,并能在复杂图形中找出这些变换.
【自主学习】
一、知识链接
1.
两个相似多边形,如果它们对应顶点所在的直线相交于一点,我们就把这样的两个图形叫做
,这个交点叫做
.位似图形上任意一对对应点到位似中心的距离之比等于
,
对应线段
.
2.
如何判断两个图形是不是位似图形?
3.
画位似图形的一般步骤有哪些?
4.
位似的基本模型:
【合作探究】
要点探究
探究点1:平面直角坐标系中的位似变换
观察1
在平面直角坐标系中,有两点
A
(6,3),B
(6,0).以原点
O
为位似中心,相似比为,把线段
AB
缩小,观察对应点之间坐标的变化.
回答1
如图,把
AB
缩小后
A,B
的对应点为
A′
(
,
),
B'
(
,
);A"
(
,
),B"
(
,
).
观察1
△AOC
三个顶点坐标分别为
A
(4,4),O
(0,0),C
(5,0),以点
O
为位似中心,相似比为
2,将△AOC
放大,观察对应顶点坐标的变化.
回答2
如图,把
△AOC
放大后
A,O,C
的对应点为
A'
(
,
),C'
(
,
);A"
(
,
),C"
(
,
).
思考
1.在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?
2.所作位似图形与原图形在原点的同侧,那么对应顶点的坐标的比与其相似比是何关系?如果所作位似图形与原图形在原点的异侧呢?
【要点归纳】1.
在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可作两个.
2.
当位似图形在原点同侧时,其对应顶点的坐标的比为
k;当位似图形在原点两侧时,其对应顶点的坐标的比为-k.(位似中的相似比k一般指新图形与原图形的比)
3.
当
k>1
时,图形扩大为原来的
k
倍;当
0<k<1时,图形缩小为原来的.
【针对训练】1.
如图,线段
AB
两个端点的坐标分别为
A
(4,4),B
(6,2),以原点
O
为位似中心,在第一象限内将线段
AB
缩小为原来的后得到线段
CD,则端点
D
的坐标为(
)
A.
(2,2)
B.
(2,1)
C.
(3,2)
D.
(3,1)
2.
△ABC
三个顶点
A
(3,6),B
(6,2),C
(2,-1),以原点为位似中心,得到的位似图形
△A′B′C′
三个顶点分别为
A′
(1,2),B′
(2,),C′
(,),则
△A′B′C′
与
△ABC
的位似比是
.
【典例精析】
例1
如图,在平面直角坐标系中,△ABO
三个顶点的坐标分别为
A
(-2,4),B
(-2,0),O
(0,0).
以原点
O
为位似中心,画出一个三角形使它与
△ABO
的相似比为.
【提示】画三角形关键是确定它各顶点的坐标.
根据前面的归纳可知,点
A
的对应点
A′
的坐标为,即(-3,6),类似地,可以确定其他顶点的坐标.
【针对训练】在平面直角坐标系中,四边形
OABC
的顶点坐标分别为
O
(0,0),A
(6,0),B
(3,6),C
(-3,3).
以原点
O
为位似中心,画出四边形
OABC
的位似图形,使它与四边形
OABC
的相似是
2
:
3.
探究点2:平面直角坐标系中的图形变换
思考
至此,我们已经学习了四种变换:平移、轴对称、旋转和位似,你能说出它们之间的异同吗?在如图所示的图案中,你能找到这些变换吗?
【针对训练】将图中的
△ABC
做下列变换,画出相应的图形,指出三个顶点的坐标所发生的变化.(每个小方格的长度为1个单位长度)
(1)
沿
y
轴正向平移
3
个单位长度;
(2)
关于
x
轴对称;
(3)
在点C的左侧,以
点C
为位似中心,将△ABC
放大为原来的2倍;
(4)
以
C
为中心,将△ABC
顺时针旋转180°.
二、课堂小结
【达标练习】
1.
将平面直角坐标系中某个图形的各点坐标做如下变化,其中属于位似变换的是(
)
A.
将各点的纵坐标乘以
2,横坐标不变
B.
将各点的横坐标除以
2,纵坐标不变
C.
将各点的横坐标、纵坐标都乘以
2
D.
将各点的纵坐标减去
2,横坐标加上
2
2.
如图,小朋在坐标系中以A为位似中心画了两个位似的直角三角形,可不小心把
E
点弄脏了,则
E
点坐标为
(
)
A.(4,-3)
B.(4,-2)
C.(4,-4)
D.(4,-6)
第2题图
第3题图
3.
如图,某学习小组在讨论
“变化的鱼”时,知道大鱼与小鱼是位似图形,则小鱼上的点
(a,b)
对应大鱼上的点
.
4.
原点
O
是
△ABC
和
△A′B′C′
的位似中心,点
A
(1,0)
与点
A′
(-2,0)
是对应点,△ABC
的面积是,则
△A′B′C′的面积是
.
5.
△ABC
三个顶点坐标分别为
A
(2,-2),B
(4,-5),C
(5,-2),以原点
O
为位似中心,将这个三角形放大为原来的
2
倍.
6.
在
13×13
的网格图中,已知
△ABC
和点
M
(1,2).
(1)
以点
M
为位似中心,位似比为
2,画出
△ABC的位似图形
△A′B′C′;
(2)
写出
△A′B′C′
的各顶点坐标.
7.
如图,点
A
的坐标为
(3,4),点
O
的坐标为
(0,0),点
B
的坐标为
(4,0).
(1)
将
△AOB
沿
x
轴向左平移1
个单位长度后得△A1O1B1,则点
A1
的坐标为
,△A1O1B1的面积为
;
(2)
将
△AOB
绕原点旋转
180°后得
△A2O2B2,则点
A2
的坐标为
;
(3)
将
△AOB
沿
x
轴翻折后得
△A3O3B3,则点
A3
的坐标为
;
(4)
以
O
为位似中心,按比例尺
1
:
2
将
△AOB
放大后得
△A4O4B4,若点
B4
在
x
轴负半轴上,则点
A4的坐标为
,△A4O4B4的面积为
.
拓展提升:
8.
如图,正方形
ABCD
和正方形
OEFG
中,点
A
和点
F
的坐标分别为
(3,2),(-1,-1),则两个正方形的位似中心的坐标是
.
【分析】此时两个正方形位似,但未指明对应的点,因此需要分类讨论
参考答案
自主学习
一、知识链接
1.
位似图形
位似中心
相似比
平行或在同一条直线上
2.
解:看它的对应点的连线是否交于一点
3.
解:过位似中心与其他各个顶点各作一条直线,按位似比在直线截取对应长度的线段,依次连接.
合作探究
一、要点探究
探究点1:平面直角坐标系中的位似变换
回答1
2
1
2
0
-2
-1
-2
0
回答2
8
8
10
0
-8
-8
-10
0
【针对训练】1.
D
2.1:3
【典例精析】
例1
解:利用位似中对应点的坐标的变化规律,分别取点
A′
(-3,6),B′
(-3,0),O
(0,0).顺次连接点
A′
,B′
,O,所得的
△A′
B′
O
就是要画的一个图形.
【针对训练】解:画法一:将四边形
OABC
各顶点的坐标都乘;在平面直角坐标系中描点O
(0,0),A'
(4,0),B'
(2,4),C′
(-2,2),用线段顺次连接O,A',B',C'.
画法二:将四边形
OABC
各顶点的坐标都乘;在平面直角坐标系中描点O
(0,0),
A″
(-4,0),B″
(-2,-4),C″
(2,-2),用线段顺次连接O,A″,B″,C″.
探究点2:平面直角坐标系中的图形变换
【针对训练】解:(1)如图中红色三角形,横坐标不变,纵坐标加3;
(2)如图中蓝色三角形,纵坐标互为相反数;
(3)如图中粉色三角形,C不变,A横纵坐标均为-2,B的横坐标-1,纵坐标+1.
(4)如图中绿色三角形,C不变,A的横纵坐标均加4,B的横坐标加2,纵坐标-2.
当堂检测
1.
C
2.
A
3.
(-2a,-2b)
4.
6
5.
解:点的坐标为A'
(4,-4),B'
(8,-10),C'
(10,-4);A″
(-4,4),B″
(-8,10),C″
(-10,4).
6.
解:(1)如图所示.
(2)△A′B′C′
的各顶点坐标分别为
A′
(3,6),B′
(5,2),C′
(11,4).
7.
(1)
(2,4)
8
(2)
(-4,-3)
(3)
(3,-4)
(4)
(-6,-8)
32
拓展提升:
8.
(1,0)
或
(-5,-2)
