华师大版九年级数学上册 23章 图形的相似 单元检测题(word版,含答案)
文档属性
| 名称 | 华师大版九年级数学上册 23章 图形的相似 单元检测题(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 261.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 00:00:00 | ||
图片预览




文档简介
第23章检测题
时间:100分钟 满分:120分
一、选择题(每小题3分,共30分)
1.下列四条线段为成比例线段的是(
)
A.1
cm,2
cm,4
cm,6
cm
B.2
cm,3
cm,4
cm,6
cm
C.8
cm,5
cm,4
cm,3
cm
D.3
cm,6
cm,9
cm,12
cm
2.如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若=,则=(
)
A.
B.
C.
D.1
3.制作一块3
m×2
m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是(
)
A.360元
B.720元
C.1080元
D.2160元
4.在平面直角坐标系中,△OAB各顶点的坐标分别为:O(0,0),A(1,2),B(0,3),以O为位似中心,△OA′B′与△OAB位似,若B点的对应点B′的坐标为(0,-6),则A点的对应点A′坐标为(
)
A.(-2,-4)
B.(-4,-2)
C.(-1,-4)
D.(1,-4)
5.如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为(
)
A.2
B.4
C.6
D.8
,第5题图)
6.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为(
)
A.五丈
B.四丈五尺
C.一丈
D.五尺
,第6题图)
7.如图,点P是线段AB上一点,AD与BC交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则图中相似三角形有(
)
A.1对
B.2对
C.3对
D.4对
,第7题图)
8.如图,在△ABC中,点D,E分别是边AC,AB的中点,BD与CE交于点O,连结DE.下列结论:①=;②=;③=;④=.其中正确的个数有(
)
A.1个
B.2个
C.3个
D.4个
,第8题图)
9.如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则的值是(
)
A.
B.
C.
D.
,第9题图)
10.如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连结AF,CF,CF与AB交于G.有以下结论:①AE=BC;②AF=CF;③BF2=FG·FC;④EG·AE=BG·AB.其中正确的个数是(
)
A.1
B.2
C.3
D.4
,第10题图)
二、填空题(每小题3分,共24分)
11.已知:=,则的值是
.
12.如图所示,点E是平行四边形ABCD的边BC延长线上一点,连结AE,交CD于点F,连结BF.写出图中任意一对相似三角形:
.
,第12题图)
13.若△ABC与△DEF相似且面积之比为25∶16,则△ABC与△DEF的周长之比为
.
14.如图,在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连结DE,CD,如果DE=2.5,那么△ACD的周长是
.
,第14题图)
15.如图,已知正方形DEFG的顶点D,E在△ABC的边BC上,顶点G,F分别在边AB,AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是
.
,第15题图)
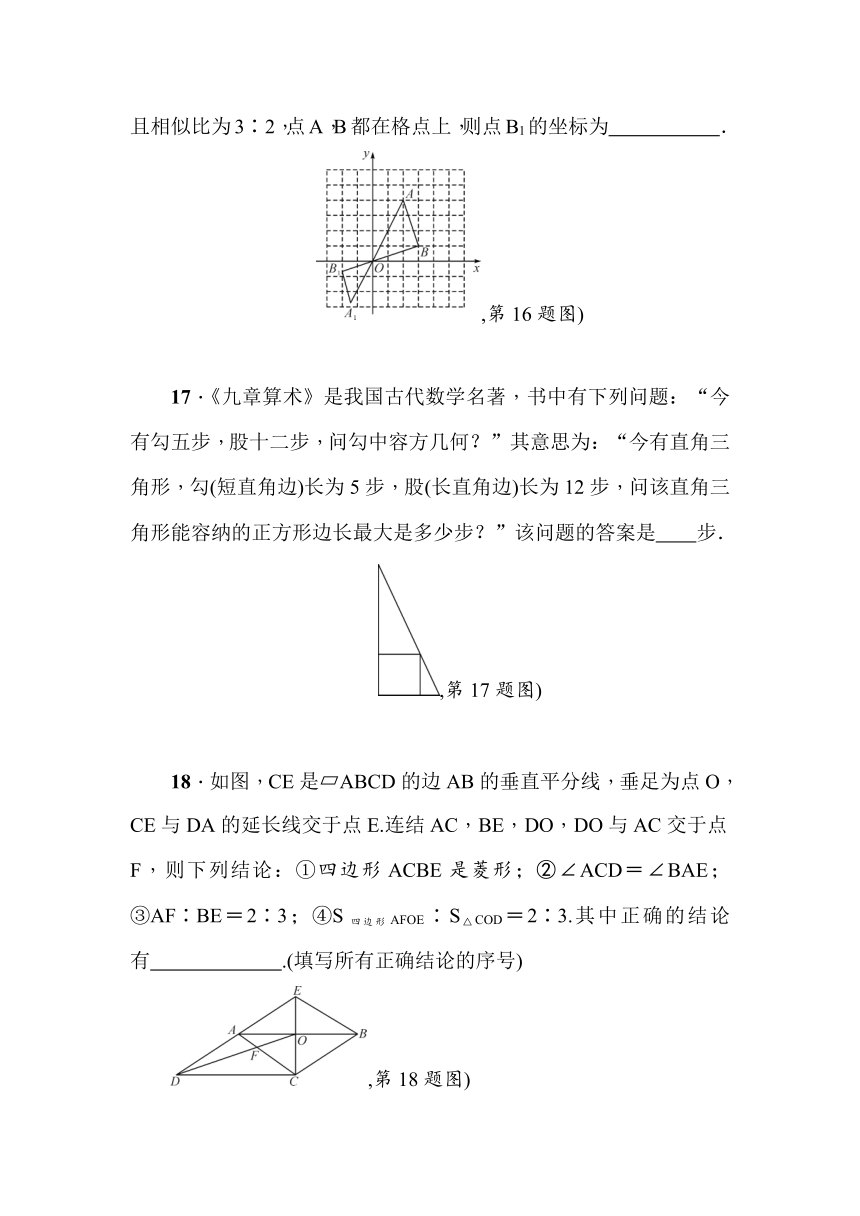
16.如图,在平面直角坐标系中,每个小方格都是边长为1个单位长度的正方形,已知△AOB与△A1OB1位似,位似中心为原点O,且相似比为3∶2,点A,B都在格点上,则点B1的坐标为
.
,第16题图)
17.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是
步.
,第17题图)
18.如图,CE是?ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E.连结AC,BE,DO,DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②∠ACD=∠BAE;③AF∶BE=2∶3;④S四边形AFOE∶S△COD=2∶3.其中正确的结论有
.(填写所有正确结论的序号)
,第18题图)
三、解答题(共66分)
19.(8分)已知△ABC三个顶点的坐标分别为A(-2,-2),B(-5,-4),C(-1,-5).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2,并写出点B2的坐标.
20.(8分)如图,已知AB∥CD,AD,BC相交于点E,F为BC上一点,且∠EAF=∠C.求证:(1)∠EAF=∠B;(2)AF2=FE·FB.
21.(8分)如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
22.(8分)某一天,小明和小亮来到一河边,想用遮阳帽和皮尺来测量这条河流的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择了一点B(点B与河对岸边上的一棵树的底部点D所确定的直线垂直于河岸).
(1)小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面的距离AB=1.7米;
(2)小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6米,小明的眼睛距离地面的距离CB=1.2米.
根据以上测量过程及测量数据,请你求出河宽BD是多少米.
23.(10分)如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,连结DE交边AB于点F,连结AC交DE于点G,且=.
(1)求证:AB∥CD;
(2)如果AD2=DG·DE,求证:=.
24.(10分)如图,在正方形ABCD中,点E,F分别是边AD,BC的中点,连结DF,过点E作EH⊥DF,垂足为H,EH的延长线交DC于点G.
(1)猜想DG与CF的数量关系,并证明你的结论;
(2)过点H作MN∥CD,分别交AD,BC于点M,N,若正方形ABCD的边长为10,点P是MN上一点,求△PDC周长的最小值.
25.(14分)如图①,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连结BO交AD于点F,OE⊥OB交BC边于点E.
(1)求证:△ABF∽△COE;
(2)当点O为AC的中点,=2时,如图②,求的值;
(3)当点O为AC的中点,=n时,请直接写出的值.
答案:
1.
B
2.
B
3.
C
4.
A
5.
B
6.
B
7.
C
8.
B
9.
C
10.
C
11.
-
12.
△ADF∽△ECF
13.
5∶4
14.
18
15.
16.
(-2,-)
17.
18.
①②④
19.
解:
(1)如图所示:△A1B1C1即为所求 (2)如图所示:△A2B2C2即为所求;B2(10,8)
20.
解:(1)∵AB∥CD,∴∠B=∠C,又∠C=∠EAF,∴∠EAF=∠B
(2)∵∠EAF=∠B,∠AFE=∠BFA,∴△AFE∽△BFA,则=,∴AF2=FE·FB
21.
解:(1)∵∠C=90°,△ACD沿AD折叠,∴∠C=∠AED=90°,∴∠DEB=∠C=90°,又∵∠B=∠B,∴△BDE∽△BAC (2)由勾股定理得AB=10,由折叠的性质知AE=AC=6,DE=CD,∠AED=∠C=90°,∴BE=AB-AE=10-6=4.由(1)知△BDE∽△BAC,∴=,∴DE=·AC=×6=3,在Rt△ADE中,由勾股定理得AD2=AE2+ED2,即AD2=62+32,∴AD=3
22.
解:易证△EBC∽△DBA,则有=,∴=,∴BD=13.6.答:河宽BD是13.6米
23.
解:(1)∵AD∥BC,∴△ADG∽△CEG,∴=,∵=,∴=,∴AB∥CD (2)AD∥BC,∴△ADG∽△CEG,∴=,∴=,∴=.∵AD2=DG·DE,∴=,∵AD∥BC,∴=,∴=
24.
解:(1)结论:CF=2DG.理由:∵四边形ABCD是正方形,∴AD=BC=CD=AB,∠ADC=∠C=90°,∵DE=AE,∴AD=CD=2DE,∵EG⊥DF,∴∠DHG=90°,∴∠CDF+∠DGE=90°,∠DGE+∠DEG=90°,∴∠CDF=∠DEG,∴△DEG∽△CDF,∴==,∴CF=2DG
(2)如图,作点C关于NM的对称点K,连结DK交MN于点P,连结PC,此时△PDC的周长最短.周长的最小值=CD+PD+PC=CD+PD+PK=CD+DK.由题意,得CD=AD=10,ED=AE=5,DG=,EG=,DH==,∴EH=2DH=2,∴HM==2,∴DM=CN=NK==1,在Rt△DCK中,DK===2,∴△PCD的周长的最小值为10+2
25.
解:(1)∵AD⊥BC,∴∠DAC+∠C=90°.∵∠BAC=90°,∴∠DAC+∠BAF=90°,∴∠BAF=∠C.∵OE⊥OB,∴∠BOA+∠COE=90°,∵∠BOA+∠ABF=90°,∴∠ABF=∠COE,∴△ABF∽△COE (2)过点O作AC垂线交BC于点H,则OH∥AB,由(1)得∠ABF=∠COE,∠BAF=∠C,∴∠AFB=∠OEC,∴∠AFO=∠HEO,而∠BAF=∠C,∴∠FAO=∠EHO,∴△OEH∽△OFA,∴OA∶OH=OF∶OE,又∵O为AC的中点,OH∥AB,∴OH为△ABC的中位线,∴OH=AB,OA=OC=AC,而=2,∴OA∶OH=2∶1,∴OF∶OE=2∶1,即=2 (3)=n
时间:100分钟 满分:120分
一、选择题(每小题3分,共30分)
1.下列四条线段为成比例线段的是(
)
A.1
cm,2
cm,4
cm,6
cm
B.2
cm,3
cm,4
cm,6
cm
C.8
cm,5
cm,4
cm,3
cm
D.3
cm,6
cm,9
cm,12
cm
2.如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若=,则=(
)
A.
B.
C.
D.1
3.制作一块3
m×2
m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是(
)
A.360元
B.720元
C.1080元
D.2160元
4.在平面直角坐标系中,△OAB各顶点的坐标分别为:O(0,0),A(1,2),B(0,3),以O为位似中心,△OA′B′与△OAB位似,若B点的对应点B′的坐标为(0,-6),则A点的对应点A′坐标为(
)
A.(-2,-4)
B.(-4,-2)
C.(-1,-4)
D.(1,-4)
5.如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为(
)
A.2
B.4
C.6
D.8
,第5题图)
6.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为(
)
A.五丈
B.四丈五尺
C.一丈
D.五尺
,第6题图)
7.如图,点P是线段AB上一点,AD与BC交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则图中相似三角形有(
)
A.1对
B.2对
C.3对
D.4对
,第7题图)
8.如图,在△ABC中,点D,E分别是边AC,AB的中点,BD与CE交于点O,连结DE.下列结论:①=;②=;③=;④=.其中正确的个数有(
)
A.1个
B.2个
C.3个
D.4个
,第8题图)
9.如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则的值是(
)
A.
B.
C.
D.
,第9题图)
10.如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连结AF,CF,CF与AB交于G.有以下结论:①AE=BC;②AF=CF;③BF2=FG·FC;④EG·AE=BG·AB.其中正确的个数是(
)
A.1
B.2
C.3
D.4
,第10题图)
二、填空题(每小题3分,共24分)
11.已知:=,则的值是
.
12.如图所示,点E是平行四边形ABCD的边BC延长线上一点,连结AE,交CD于点F,连结BF.写出图中任意一对相似三角形:
.
,第12题图)
13.若△ABC与△DEF相似且面积之比为25∶16,则△ABC与△DEF的周长之比为
.
14.如图,在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连结DE,CD,如果DE=2.5,那么△ACD的周长是
.
,第14题图)
15.如图,已知正方形DEFG的顶点D,E在△ABC的边BC上,顶点G,F分别在边AB,AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是
.
,第15题图)
16.如图,在平面直角坐标系中,每个小方格都是边长为1个单位长度的正方形,已知△AOB与△A1OB1位似,位似中心为原点O,且相似比为3∶2,点A,B都在格点上,则点B1的坐标为
.
,第16题图)
17.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是
步.
,第17题图)
18.如图,CE是?ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E.连结AC,BE,DO,DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②∠ACD=∠BAE;③AF∶BE=2∶3;④S四边形AFOE∶S△COD=2∶3.其中正确的结论有
.(填写所有正确结论的序号)
,第18题图)
三、解答题(共66分)
19.(8分)已知△ABC三个顶点的坐标分别为A(-2,-2),B(-5,-4),C(-1,-5).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2,并写出点B2的坐标.
20.(8分)如图,已知AB∥CD,AD,BC相交于点E,F为BC上一点,且∠EAF=∠C.求证:(1)∠EAF=∠B;(2)AF2=FE·FB.
21.(8分)如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
22.(8分)某一天,小明和小亮来到一河边,想用遮阳帽和皮尺来测量这条河流的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择了一点B(点B与河对岸边上的一棵树的底部点D所确定的直线垂直于河岸).
(1)小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面的距离AB=1.7米;
(2)小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6米,小明的眼睛距离地面的距离CB=1.2米.
根据以上测量过程及测量数据,请你求出河宽BD是多少米.
23.(10分)如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,连结DE交边AB于点F,连结AC交DE于点G,且=.
(1)求证:AB∥CD;
(2)如果AD2=DG·DE,求证:=.
24.(10分)如图,在正方形ABCD中,点E,F分别是边AD,BC的中点,连结DF,过点E作EH⊥DF,垂足为H,EH的延长线交DC于点G.
(1)猜想DG与CF的数量关系,并证明你的结论;
(2)过点H作MN∥CD,分别交AD,BC于点M,N,若正方形ABCD的边长为10,点P是MN上一点,求△PDC周长的最小值.
25.(14分)如图①,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连结BO交AD于点F,OE⊥OB交BC边于点E.
(1)求证:△ABF∽△COE;
(2)当点O为AC的中点,=2时,如图②,求的值;
(3)当点O为AC的中点,=n时,请直接写出的值.
答案:
1.
B
2.
B
3.
C
4.
A
5.
B
6.
B
7.
C
8.
B
9.
C
10.
C
11.
-
12.
△ADF∽△ECF
13.
5∶4
14.
18
15.
16.
(-2,-)
17.
18.
①②④
19.
解:
(1)如图所示:△A1B1C1即为所求 (2)如图所示:△A2B2C2即为所求;B2(10,8)
20.
解:(1)∵AB∥CD,∴∠B=∠C,又∠C=∠EAF,∴∠EAF=∠B
(2)∵∠EAF=∠B,∠AFE=∠BFA,∴△AFE∽△BFA,则=,∴AF2=FE·FB
21.
解:(1)∵∠C=90°,△ACD沿AD折叠,∴∠C=∠AED=90°,∴∠DEB=∠C=90°,又∵∠B=∠B,∴△BDE∽△BAC (2)由勾股定理得AB=10,由折叠的性质知AE=AC=6,DE=CD,∠AED=∠C=90°,∴BE=AB-AE=10-6=4.由(1)知△BDE∽△BAC,∴=,∴DE=·AC=×6=3,在Rt△ADE中,由勾股定理得AD2=AE2+ED2,即AD2=62+32,∴AD=3
22.
解:易证△EBC∽△DBA,则有=,∴=,∴BD=13.6.答:河宽BD是13.6米
23.
解:(1)∵AD∥BC,∴△ADG∽△CEG,∴=,∵=,∴=,∴AB∥CD (2)AD∥BC,∴△ADG∽△CEG,∴=,∴=,∴=.∵AD2=DG·DE,∴=,∵AD∥BC,∴=,∴=
24.
解:(1)结论:CF=2DG.理由:∵四边形ABCD是正方形,∴AD=BC=CD=AB,∠ADC=∠C=90°,∵DE=AE,∴AD=CD=2DE,∵EG⊥DF,∴∠DHG=90°,∴∠CDF+∠DGE=90°,∠DGE+∠DEG=90°,∴∠CDF=∠DEG,∴△DEG∽△CDF,∴==,∴CF=2DG
(2)如图,作点C关于NM的对称点K,连结DK交MN于点P,连结PC,此时△PDC的周长最短.周长的最小值=CD+PD+PC=CD+PD+PK=CD+DK.由题意,得CD=AD=10,ED=AE=5,DG=,EG=,DH==,∴EH=2DH=2,∴HM==2,∴DM=CN=NK==1,在Rt△DCK中,DK===2,∴△PCD的周长的最小值为10+2
25.
解:(1)∵AD⊥BC,∴∠DAC+∠C=90°.∵∠BAC=90°,∴∠DAC+∠BAF=90°,∴∠BAF=∠C.∵OE⊥OB,∴∠BOA+∠COE=90°,∵∠BOA+∠ABF=90°,∴∠ABF=∠COE,∴△ABF∽△COE (2)过点O作AC垂线交BC于点H,则OH∥AB,由(1)得∠ABF=∠COE,∠BAF=∠C,∴∠AFB=∠OEC,∴∠AFO=∠HEO,而∠BAF=∠C,∴∠FAO=∠EHO,∴△OEH∽△OFA,∴OA∶OH=OF∶OE,又∵O为AC的中点,OH∥AB,∴OH为△ABC的中位线,∴OH=AB,OA=OC=AC,而=2,∴OA∶OH=2∶1,∴OF∶OE=2∶1,即=2 (3)=n
