苏科版七年级数学上册第五章《走进图形世界》单元检测(2)(Word版 含答案)
文档属性
| 名称 | 苏科版七年级数学上册第五章《走进图形世界》单元检测(2)(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 601.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 23:06:53 | ||
图片预览

文档简介
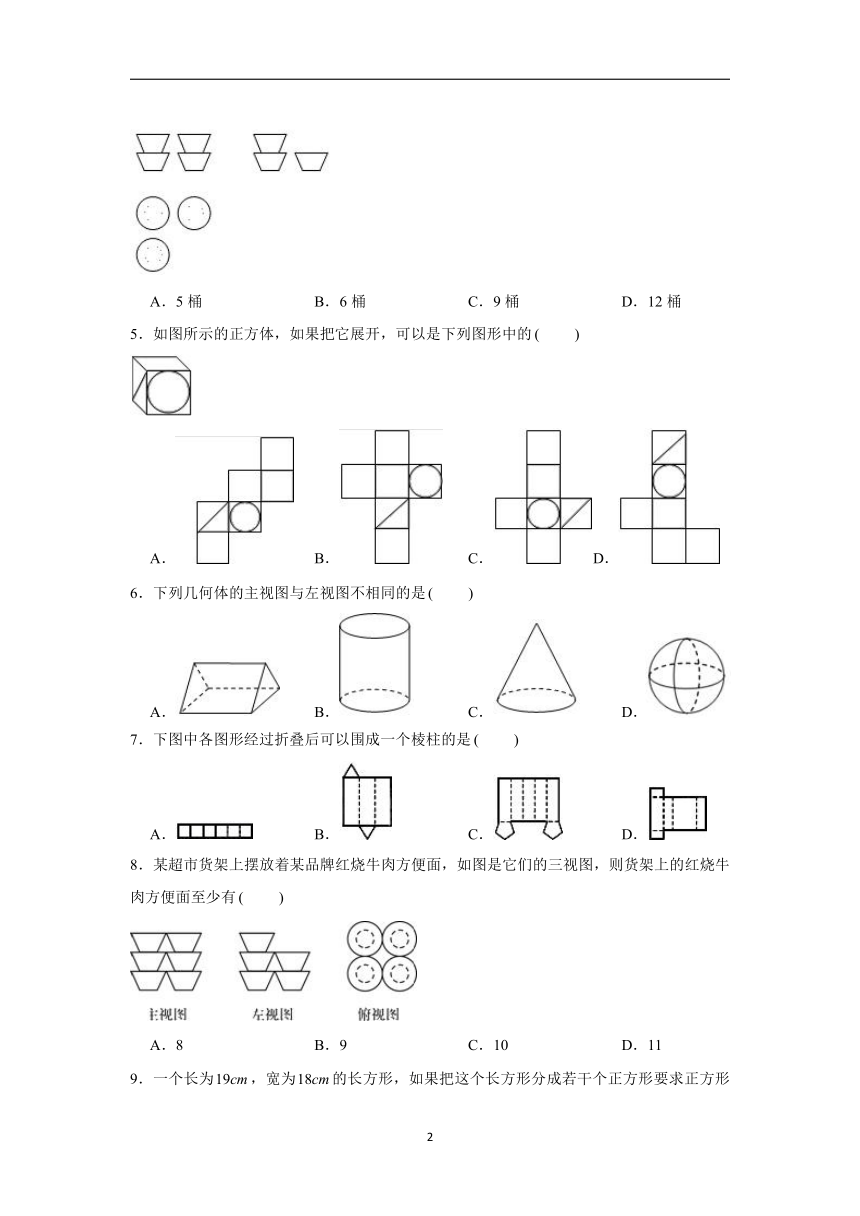
第五章《走进图形世界》单元检测(2)
一.选择题
1.一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到的这个几何体的形状图是
A.B.C.D.
2.(2020?德阳)如图是一个几何体的三视图,根据图中所示数据计算这个几何体的表面积是
A.
B.
C.
D.
3.一个几何体的主视图、左视图、俯视图都是圆形,这个几何体可能是
A.圆柱
B.圆锥
C.球
D.半球
4.若干个桶装方便面摆放在桌子上,小明从三个不同方向看到的图形如图所示,则这一堆方便面共有
A.5桶
B.6桶
C.9桶
D.12桶
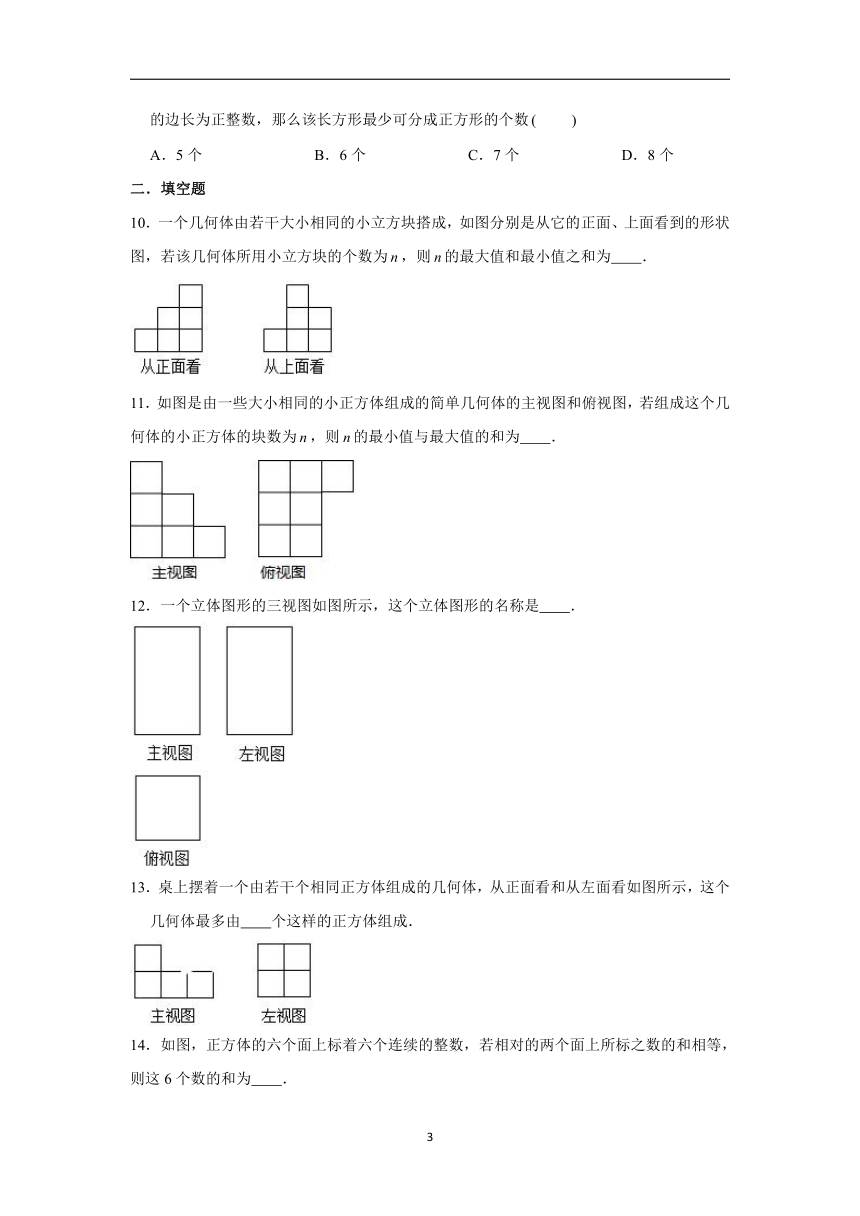
5.如图所示的正方体,如果把它展开,可以是下列图形中的
A.
B.
C.D.
6.下列几何体的主视图与左视图不相同的是
A.
B.
C.
D.
7.下图中各图形经过折叠后可以围成一个棱柱的是
A.
B.
C.
D.
8.某超市货架上摆放着某品牌红烧牛肉方便面,如图是它们的三视图,则货架上的红烧牛肉方便面至少有
A.8
B.9
C.10
D.11
9.一个长为,宽为的长方形,如果把这个长方形分成若干个正方形要求正方形的边长为正整数,那么该长方形最少可分成正方形的个数
A.5个
B.6个
C.7个
D.8个
二.填空题
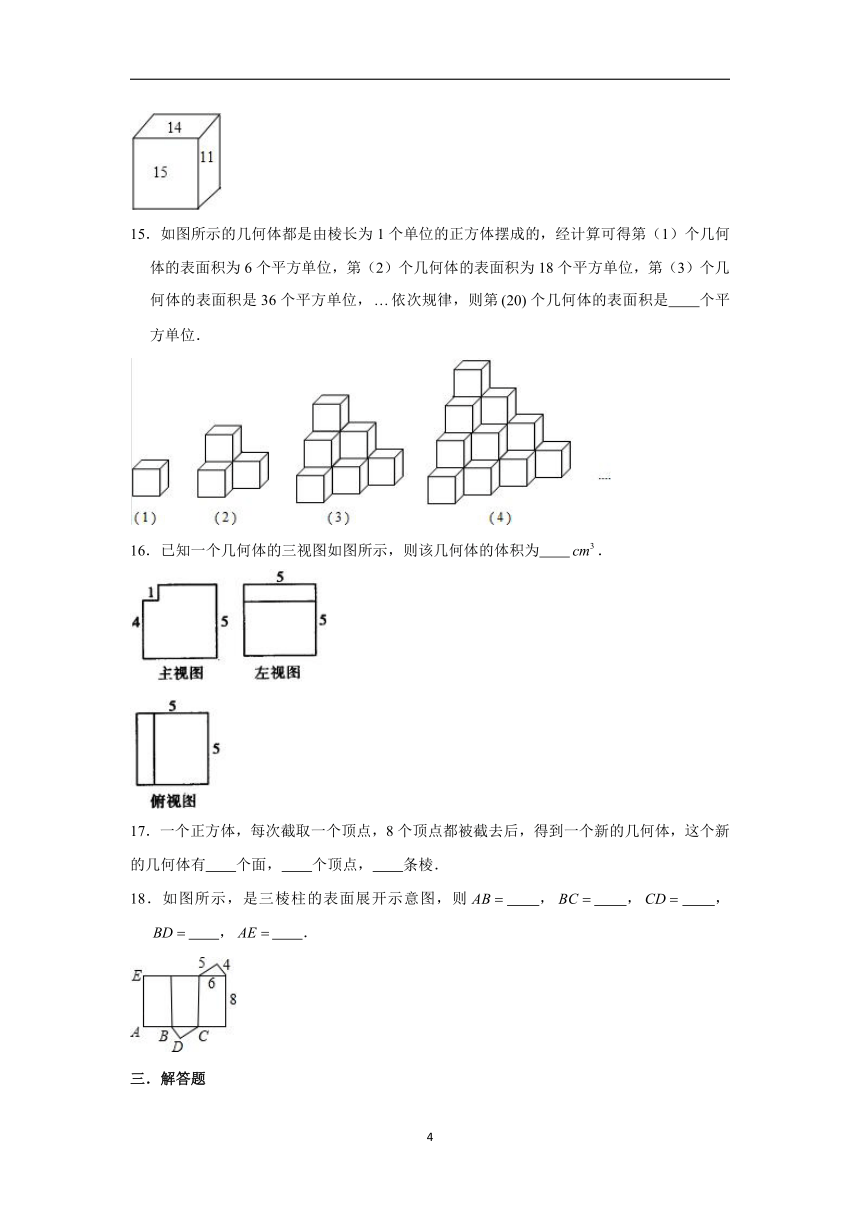
10.一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,若该几何体所用小立方块的个数为,则的最大值和最小值之和为 .
11.如图是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图,若组成这个几何体的小正方体的块数为,则的最小值与最大值的和为 .
12.一个立体图形的三视图如图所示,这个立体图形的名称是 .
13.桌上摆着一个由若干个相同正方体组成的几何体,从正面看和从左面看如图所示,这个几何体最多由 个这样的正方体组成.
14.如图,正方体的六个面上标着六个连续的整数,若相对的两个面上所标之数的和相等,则这6个数的和为 .
15.如图所示的几何体都是由棱长为1个单位的正方体摆成的,经计算可得第(1)个几何体的表面积为6个平方单位,第(2)个几何体的表面积为18个平方单位,第(3)个几何体的表面积是36个平方单位,依次规律,则第个几何体的表面积是 个平方单位.
16.已知一个几何体的三视图如图所示,则该几何体的体积为 .
17.一个正方体,每次截取一个顶点,8个顶点都被截去后,得到一个新的几何体,这个新的几何体有 个面, 个顶点, 条棱.
18.如图所示,是三棱柱的表面展开示意图,则 , , , , .
三.解答题
19.如图是由若干个大小相同的小正方体搭成的几何体,请画出从正面、左面、上面看到的这个几何体的形状图.
20.如图是小明10块棱长都为的正方体搭成的几何体.
(1)分别画出从正面、从左面、从上面看到的所搭几何体的形状图;
(2)小明所搭几何体的表面积(包括与桌面接触的部分)是 .
21.工厂生产某种零件,其示意图如下(单位:.
(1)该零件的主视图如图所示,请分别画出它的左视图和俯视图;
(2)如果要给该零件的表面涂上防锈漆,请你计算需要涂漆的面积.
22.如图是由7个相同小正方体组成的几何体,请在方格纸中分别画出它的三个视图.
23.如图所示是由几个小立方体所组成几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的从正面看和从左面看的形状图.
24.按要求完成下列视图问题
(1)如图(一,它是由6个同样大小的正方体摆成的几何体.将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?
(2)如图(二,请你借助图四虚线网格画出该几何体的俯视图.
(3)如图(三,它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助图四虚线网格画出该几何体的主视图.
25.(1)如图1是由大小相同的小立方块搭成的几何体,请在图2的方格中画出从上面和左面看到的该几何体的形状图.(只需用铅笔将虚线化为实线)
(2)若要用大小相同的小立方块搭一个几何体,使得它从上面和左面看到的形状图与你在图2方格中所画的形状图相同,则搭这样的一个几何体最大需要 个小立方块.
26.如图是小强用八块相同的小立方体搭成的一个几何体,从正面、左面和上面观察这个几何体,请你在下面相应的位置分别画出你所看到的几何体的形状图(在答题卡上画完图后请用黑色签字笔描图)
27.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:已知这个长方体纸盒高为,底面是一个正方形,并且这个长方体纸盒所有棱长的和是,求这个长方体纸盒的体积.
28.棱长为的正方体,摆成如图所示的形状.
(1)如果这一物体摆放三层,试求该物体的表面积;
(2)依图中摆放方法类推,如果该物体摆放了上下20层,求该物体的表面积.
(3)依图中摆放方法类推,如果该物体摆放了上下层,求该物体的表面积.
一.选择题
1.(2020秋?和平区期中)一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到的这个几何体的形状图是
A.
B.
C.D.
【解答】解:根据所给出的图形和数字可得:
主视图有4列,每列小正方形数目分别为1,2,3,2,
则符合题意的是;
故选:.
2.(2020?德阳)如图是一个几何体的三视图,根据图中所示数据计算这个几何体的表面积是
A.
B.
C.
D.
【解答】解:这个几何体的表面积,
故选:.
3.(2020?梁溪区一模)一个几何体的主视图、左视图、俯视图都是圆形,这个几何体可能是
A.圆柱
B.圆锥
C.球
D.半球
【解答】解:一个几何体的主视图、左视图、俯视图都是圆形,这个几何体可能是球,
故选:.
4.(2019秋?无为县期末)若干个桶装方便面摆放在桌子上,小明从三个不同方向看到的图形如图所示,则这一堆方便面共有
A.5桶
B.6桶
C.9桶
D.12桶
【解答】解:根据三视图的形状,可得到,俯视图上每个位置上放置的个数,进而得出总数量,
俯视图中的数,表示该位置放的数量,因此,
故选:.
5.(2017?双流区校级自主招生)如图所示的正方体,如果把它展开,可以是下列图形中的
A.
B.
C.D.
【解答】解:由“相间端是对面”可知、不符合题意,而折叠后,圆形在前面,正方形在上面,则三角形的面在右面,与原图不符,
只有折叠后符合,
故选:.
6.(2019秋?建湖县期末)下列几何体的主视图与左视图不相同的是
A.
B.
C.
D.
【解答】解:三棱柱的主视图为长方形,左视图是三角形,因此选项符合题意;
圆柱体的主视图、左视图都是长方形,因此选项不符合题意;
圆锥体的主视图、左视图都是三角形,因此选项不符合题意;
球体的主视图、左视图包括俯视图都是圆形的,因此选项不符合题意;
故选:.
7.(2020秋?沈河区校级月考)下图中各图形经过折叠后可以围成一个棱柱的是
A.
B.
C.
D.
【解答】解:选项缺少两个底面,不能围成棱柱;选项中折叠后没有上底面,不能折成棱柱,选项不能组成棱柱,是因为上下两底面四个边的长不能与侧面的边等长、重合.,只有能围成三棱柱.
故选:.
8.(2013?自贡)某超市货架上摆放着某品牌红烧牛肉方便面,如图是它们的三视图,则货架上的红烧牛肉方便面至少有
A.8
B.9
C.10
D.11
【解答】解:易得第一层有4碗,第二层最少有3碗,第三层最少有2碗,所以至少共有9个碗.
故选:.
9.一个长为,宽为的长方形,如果把这个长方形分成若干个正方形要求正方形的边长为正整数,那么该长方形最少可分成正方形的个数
A.5个
B.6个
C.7个
D.8个
【解答】解:7个正方形边长分别11,8,7,7,5,5,3.
另外,不可能分成5个或6个正方形,这个证明很麻烦,大概过程是通过编程列出所有可能的组合(如所有满足5个或6个数平方之和等于且最大两个和不超过19的整数组合),然后对每个组合逐一否定其可行性,所以不用担心有更少正方形的组合.
故选:.
二.填空题
10.(2020秋?武侯区校级期中)一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,若该几何体所用小立方块的个数为,则的最大值和最小值之和为 22 .
【解答】解:根据主视图、俯视图,可以得出最少时、最多时,在俯视图的相应位置上所摆放的个数如下:
最少时需要9个,最多时需要13个,
因此,
故答案为:22.
11.(2020秋?雁塔区校级月考)如图是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图,若组成这个几何体的小正方体的块数为,则的最小值与最大值的和为 26 .
【解答】解:根据主视图、俯视图,可以得出最少时、最多时,在俯视图的相应位置上所摆放的个数如下:
最少时需要10个,最多时需要16个,
因此,
故答案为:26.
12.(2019秋?辉县市期末)一个立体图形的三视图如图所示,这个立体图形的名称是 长方体 .
【解答】解:观察三视图可知,原来的几何体是长方体.
故答案为长方体.
13.(2016秋?简阳市期末)桌上摆着一个由若干个相同正方体组成的几何体,从正面看和从左面看如图所示,这个几何体最多由 8 个这样的正方体组成.
【解答】解:由主视图可得组合几何体有3列,由左视图可得组合几何体有2行,
最底层几何体最多正方体的个数为:,
由主视图和左视图可得第二层2个角各有一个正方体,
第二层共有2个正方体,
该组合几何体最多共有个正方体.
故答案为:8.
14.(2017秋?简阳市期中)如图,正方体的六个面上标着六个连续的整数,若相对的两个面上所标之数的和相等,则这6个数的和为 81 .
【解答】解:根据题意分析可得:六个面上分别写着六个连续的整数,
故六个整数可能为11,12,13,14,15,16或10,11,12,13,14,15;
且每个相对面上的两个数之和相等,
,
,
故可能为11,12,13,14,15,16或10,11,12,13,14,15,其和为81和和14必须为对面,在本体图片中,11和14为邻面,故不合题意,应舍去)
故答案为:81.
15.(2016秋?青羊区期末)如图所示的几何体都是由棱长为1个单位的正方体摆成的,经计算可得第(1)个几何体的表面积为6个平方单位,第(2)个几何体的表面积为18个平方单位,第(3)个几何体的表面积是36个平方单位,依次规律,则第个几何体的表面积是 1260 个平方单位.
【解答】解:结合图形,发现:
第个图形的表面积是个平方单位.
故答案为:1260.
16.已知一个几何体的三视图如图所示,则该几何体的体积为 120 .
【解答】解:根据图中三视图可得出其体积上下两个长方体的体积和.
17.一个正方体,每次截取一个顶点,8个顶点都被截去后,得到一个新的几何体,这个新的几何体有 14 个面, 个顶点, 条棱.
【解答】解:每截去一个顶点就会多出1个面,2个顶点和3条棱,那么得到的新的几何体就应该有个面,个顶点,条棱.
故填14、24、36.
18.如图所示,是三棱柱的表面展开示意图,则 4 , , , , .
【解答】解:由图可知,棱与与4是相对的,棱与5是相对的,棱与6是相对的,棱与8是相对的,
所以,,,,.
故填4、5、6、4、8.
三.解答题
19.(2020秋?铁西区期中)如图是由若干个大小相同的小正方体搭成的几何体,请画出从正面、左面、上面看到的这个几何体的形状图.
【解答】解:作出几何体的三视图,如图所示:
20.(2020秋?和平区期中)如图是小明10块棱长都为的正方体搭成的几何体.
(1)分别画出从正面、从左面、从上面看到的所搭几何体的形状图;
(2)小明所搭几何体的表面积(包括与桌面接触的部分)是 .
【解答】解:(1)三视图如图所示:
(2)表面积.
故答案为:.
21.(2019秋?溧水区期末)工厂生产某种零件,其示意图如下(单位:.
(1)该零件的主视图如图所示,请分别画出它的左视图和俯视图;
(2)如果要给该零件的表面涂上防锈漆,请你计算需要涂漆的面积.
【解答】解:(1)如图所示:
(2)
故需要涂漆的面积是.
22.(2019秋?大丰区期末)如图是由7个相同小正方体组成的几何体,请在方格纸中分别画出它的三个视图.
【解答】解:它的三个视图如图所示:
23.(2020秋?黄岛区校级月考)如图所示是由几个小立方体所组成几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的从正面看和从左面看的形状图.
【解答】解:如图所示:
24.(2020春?肇源县期末)按要求完成下列视图问题
(1)如图(一,它是由6个同样大小的正方体摆成的几何体.将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?
(2)如图(二,请你借助图四虚线网格画出该几何体的俯视图.
(3)如图(三,它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助图四虚线网格画出该几何体的主视图.
【解答】解:(1)如图(一,它是由6个同样大小的正方体摆成的几何体.将正方体①移走后,
新几何体的三视图与原几何体的三视图相比,左视图没有发生改变;
(2)如图1所示,
(3)如图2所示.
25.(2018秋?永安市期末)(1)如图1是由大小相同的小立方块搭成的几何体,请在图2的方格中画出从上面和左面看到的该几何体的形状图.(只需用铅笔将虚线化为实线)
(2)若要用大小相同的小立方块搭一个几何体,使得它从上面和左面看到的形状图与你在图2方格中所画的形状图相同,则搭这样的一个几何体最大需要 9 个小立方块.
【解答】解:(1)如图所示:
(2)搭这样的一个几何体最大需要个小立方块.
故答案为:9.
26.(2018秋?通川区期末)如图是小强用八块相同的小立方体搭成的一个几何体,从正面、左面和上面观察这个几何体,请你在下面相应的位置分别画出你所看到的几何体的形状图(在答题卡上画完图后请用黑色签字笔描图)
【解答】解:三视图如下:
27.(2018秋?张店区期中)小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了 8 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:已知这个长方体纸盒高为,底面是一个正方形,并且这个长方体纸盒所有棱长的和是,求这个长方体纸盒的体积.
【解答】解(1)由图可得,小明共剪了8条棱,
故答案为:8.
(2)如图,粘贴的位置有四种情况如下:
(3)长方体纸盒的底面是一个正方形,
可设底面边长,
长方体纸盒所有棱长的和是,长方体纸盒高为,
,
解得,
这个长方体纸盒的体积为:立方厘米.
28.(2018秋?温江区校级月考)棱长为的正方体,摆成如图所示的形状.
(1)如果这一物体摆放三层,试求该物体的表面积;
(2)依图中摆放方法类推,如果该物体摆放了上下20层,求该物体的表面积.
(3)依图中摆放方法类推,如果该物体摆放了上下层,求该物体的表面积.
【解答】解:(1).
故该物体的表面积为;
(2).
故该物体的表面积为;
(3).
故该物体的表面积为.
1
一.选择题
1.一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到的这个几何体的形状图是
A.B.C.D.
2.(2020?德阳)如图是一个几何体的三视图,根据图中所示数据计算这个几何体的表面积是
A.
B.
C.
D.
3.一个几何体的主视图、左视图、俯视图都是圆形,这个几何体可能是
A.圆柱
B.圆锥
C.球
D.半球
4.若干个桶装方便面摆放在桌子上,小明从三个不同方向看到的图形如图所示,则这一堆方便面共有
A.5桶
B.6桶
C.9桶
D.12桶
5.如图所示的正方体,如果把它展开,可以是下列图形中的
A.
B.
C.D.
6.下列几何体的主视图与左视图不相同的是
A.
B.
C.
D.
7.下图中各图形经过折叠后可以围成一个棱柱的是
A.
B.
C.
D.
8.某超市货架上摆放着某品牌红烧牛肉方便面,如图是它们的三视图,则货架上的红烧牛肉方便面至少有
A.8
B.9
C.10
D.11
9.一个长为,宽为的长方形,如果把这个长方形分成若干个正方形要求正方形的边长为正整数,那么该长方形最少可分成正方形的个数
A.5个
B.6个
C.7个
D.8个
二.填空题
10.一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,若该几何体所用小立方块的个数为,则的最大值和最小值之和为 .
11.如图是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图,若组成这个几何体的小正方体的块数为,则的最小值与最大值的和为 .
12.一个立体图形的三视图如图所示,这个立体图形的名称是 .
13.桌上摆着一个由若干个相同正方体组成的几何体,从正面看和从左面看如图所示,这个几何体最多由 个这样的正方体组成.
14.如图,正方体的六个面上标着六个连续的整数,若相对的两个面上所标之数的和相等,则这6个数的和为 .
15.如图所示的几何体都是由棱长为1个单位的正方体摆成的,经计算可得第(1)个几何体的表面积为6个平方单位,第(2)个几何体的表面积为18个平方单位,第(3)个几何体的表面积是36个平方单位,依次规律,则第个几何体的表面积是 个平方单位.
16.已知一个几何体的三视图如图所示,则该几何体的体积为 .
17.一个正方体,每次截取一个顶点,8个顶点都被截去后,得到一个新的几何体,这个新的几何体有 个面, 个顶点, 条棱.
18.如图所示,是三棱柱的表面展开示意图,则 , , , , .
三.解答题
19.如图是由若干个大小相同的小正方体搭成的几何体,请画出从正面、左面、上面看到的这个几何体的形状图.
20.如图是小明10块棱长都为的正方体搭成的几何体.
(1)分别画出从正面、从左面、从上面看到的所搭几何体的形状图;
(2)小明所搭几何体的表面积(包括与桌面接触的部分)是 .
21.工厂生产某种零件,其示意图如下(单位:.
(1)该零件的主视图如图所示,请分别画出它的左视图和俯视图;
(2)如果要给该零件的表面涂上防锈漆,请你计算需要涂漆的面积.
22.如图是由7个相同小正方体组成的几何体,请在方格纸中分别画出它的三个视图.
23.如图所示是由几个小立方体所组成几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的从正面看和从左面看的形状图.
24.按要求完成下列视图问题
(1)如图(一,它是由6个同样大小的正方体摆成的几何体.将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?
(2)如图(二,请你借助图四虚线网格画出该几何体的俯视图.
(3)如图(三,它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助图四虚线网格画出该几何体的主视图.
25.(1)如图1是由大小相同的小立方块搭成的几何体,请在图2的方格中画出从上面和左面看到的该几何体的形状图.(只需用铅笔将虚线化为实线)
(2)若要用大小相同的小立方块搭一个几何体,使得它从上面和左面看到的形状图与你在图2方格中所画的形状图相同,则搭这样的一个几何体最大需要 个小立方块.
26.如图是小强用八块相同的小立方体搭成的一个几何体,从正面、左面和上面观察这个几何体,请你在下面相应的位置分别画出你所看到的几何体的形状图(在答题卡上画完图后请用黑色签字笔描图)
27.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:已知这个长方体纸盒高为,底面是一个正方形,并且这个长方体纸盒所有棱长的和是,求这个长方体纸盒的体积.
28.棱长为的正方体,摆成如图所示的形状.
(1)如果这一物体摆放三层,试求该物体的表面积;
(2)依图中摆放方法类推,如果该物体摆放了上下20层,求该物体的表面积.
(3)依图中摆放方法类推,如果该物体摆放了上下层,求该物体的表面积.
一.选择题
1.(2020秋?和平区期中)一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到的这个几何体的形状图是
A.
B.
C.D.
【解答】解:根据所给出的图形和数字可得:
主视图有4列,每列小正方形数目分别为1,2,3,2,
则符合题意的是;
故选:.
2.(2020?德阳)如图是一个几何体的三视图,根据图中所示数据计算这个几何体的表面积是
A.
B.
C.
D.
【解答】解:这个几何体的表面积,
故选:.
3.(2020?梁溪区一模)一个几何体的主视图、左视图、俯视图都是圆形,这个几何体可能是
A.圆柱
B.圆锥
C.球
D.半球
【解答】解:一个几何体的主视图、左视图、俯视图都是圆形,这个几何体可能是球,
故选:.
4.(2019秋?无为县期末)若干个桶装方便面摆放在桌子上,小明从三个不同方向看到的图形如图所示,则这一堆方便面共有
A.5桶
B.6桶
C.9桶
D.12桶
【解答】解:根据三视图的形状,可得到,俯视图上每个位置上放置的个数,进而得出总数量,
俯视图中的数,表示该位置放的数量,因此,
故选:.
5.(2017?双流区校级自主招生)如图所示的正方体,如果把它展开,可以是下列图形中的
A.
B.
C.D.
【解答】解:由“相间端是对面”可知、不符合题意,而折叠后,圆形在前面,正方形在上面,则三角形的面在右面,与原图不符,
只有折叠后符合,
故选:.
6.(2019秋?建湖县期末)下列几何体的主视图与左视图不相同的是
A.
B.
C.
D.
【解答】解:三棱柱的主视图为长方形,左视图是三角形,因此选项符合题意;
圆柱体的主视图、左视图都是长方形,因此选项不符合题意;
圆锥体的主视图、左视图都是三角形,因此选项不符合题意;
球体的主视图、左视图包括俯视图都是圆形的,因此选项不符合题意;
故选:.
7.(2020秋?沈河区校级月考)下图中各图形经过折叠后可以围成一个棱柱的是
A.
B.
C.
D.
【解答】解:选项缺少两个底面,不能围成棱柱;选项中折叠后没有上底面,不能折成棱柱,选项不能组成棱柱,是因为上下两底面四个边的长不能与侧面的边等长、重合.,只有能围成三棱柱.
故选:.
8.(2013?自贡)某超市货架上摆放着某品牌红烧牛肉方便面,如图是它们的三视图,则货架上的红烧牛肉方便面至少有
A.8
B.9
C.10
D.11
【解答】解:易得第一层有4碗,第二层最少有3碗,第三层最少有2碗,所以至少共有9个碗.
故选:.
9.一个长为,宽为的长方形,如果把这个长方形分成若干个正方形要求正方形的边长为正整数,那么该长方形最少可分成正方形的个数
A.5个
B.6个
C.7个
D.8个
【解答】解:7个正方形边长分别11,8,7,7,5,5,3.
另外,不可能分成5个或6个正方形,这个证明很麻烦,大概过程是通过编程列出所有可能的组合(如所有满足5个或6个数平方之和等于且最大两个和不超过19的整数组合),然后对每个组合逐一否定其可行性,所以不用担心有更少正方形的组合.
故选:.
二.填空题
10.(2020秋?武侯区校级期中)一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,若该几何体所用小立方块的个数为,则的最大值和最小值之和为 22 .
【解答】解:根据主视图、俯视图,可以得出最少时、最多时,在俯视图的相应位置上所摆放的个数如下:
最少时需要9个,最多时需要13个,
因此,
故答案为:22.
11.(2020秋?雁塔区校级月考)如图是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图,若组成这个几何体的小正方体的块数为,则的最小值与最大值的和为 26 .
【解答】解:根据主视图、俯视图,可以得出最少时、最多时,在俯视图的相应位置上所摆放的个数如下:
最少时需要10个,最多时需要16个,
因此,
故答案为:26.
12.(2019秋?辉县市期末)一个立体图形的三视图如图所示,这个立体图形的名称是 长方体 .
【解答】解:观察三视图可知,原来的几何体是长方体.
故答案为长方体.
13.(2016秋?简阳市期末)桌上摆着一个由若干个相同正方体组成的几何体,从正面看和从左面看如图所示,这个几何体最多由 8 个这样的正方体组成.
【解答】解:由主视图可得组合几何体有3列,由左视图可得组合几何体有2行,
最底层几何体最多正方体的个数为:,
由主视图和左视图可得第二层2个角各有一个正方体,
第二层共有2个正方体,
该组合几何体最多共有个正方体.
故答案为:8.
14.(2017秋?简阳市期中)如图,正方体的六个面上标着六个连续的整数,若相对的两个面上所标之数的和相等,则这6个数的和为 81 .
【解答】解:根据题意分析可得:六个面上分别写着六个连续的整数,
故六个整数可能为11,12,13,14,15,16或10,11,12,13,14,15;
且每个相对面上的两个数之和相等,
,
,
故可能为11,12,13,14,15,16或10,11,12,13,14,15,其和为81和和14必须为对面,在本体图片中,11和14为邻面,故不合题意,应舍去)
故答案为:81.
15.(2016秋?青羊区期末)如图所示的几何体都是由棱长为1个单位的正方体摆成的,经计算可得第(1)个几何体的表面积为6个平方单位,第(2)个几何体的表面积为18个平方单位,第(3)个几何体的表面积是36个平方单位,依次规律,则第个几何体的表面积是 1260 个平方单位.
【解答】解:结合图形,发现:
第个图形的表面积是个平方单位.
故答案为:1260.
16.已知一个几何体的三视图如图所示,则该几何体的体积为 120 .
【解答】解:根据图中三视图可得出其体积上下两个长方体的体积和.
17.一个正方体,每次截取一个顶点,8个顶点都被截去后,得到一个新的几何体,这个新的几何体有 14 个面, 个顶点, 条棱.
【解答】解:每截去一个顶点就会多出1个面,2个顶点和3条棱,那么得到的新的几何体就应该有个面,个顶点,条棱.
故填14、24、36.
18.如图所示,是三棱柱的表面展开示意图,则 4 , , , , .
【解答】解:由图可知,棱与与4是相对的,棱与5是相对的,棱与6是相对的,棱与8是相对的,
所以,,,,.
故填4、5、6、4、8.
三.解答题
19.(2020秋?铁西区期中)如图是由若干个大小相同的小正方体搭成的几何体,请画出从正面、左面、上面看到的这个几何体的形状图.
【解答】解:作出几何体的三视图,如图所示:
20.(2020秋?和平区期中)如图是小明10块棱长都为的正方体搭成的几何体.
(1)分别画出从正面、从左面、从上面看到的所搭几何体的形状图;
(2)小明所搭几何体的表面积(包括与桌面接触的部分)是 .
【解答】解:(1)三视图如图所示:
(2)表面积.
故答案为:.
21.(2019秋?溧水区期末)工厂生产某种零件,其示意图如下(单位:.
(1)该零件的主视图如图所示,请分别画出它的左视图和俯视图;
(2)如果要给该零件的表面涂上防锈漆,请你计算需要涂漆的面积.
【解答】解:(1)如图所示:
(2)
故需要涂漆的面积是.
22.(2019秋?大丰区期末)如图是由7个相同小正方体组成的几何体,请在方格纸中分别画出它的三个视图.
【解答】解:它的三个视图如图所示:
23.(2020秋?黄岛区校级月考)如图所示是由几个小立方体所组成几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的从正面看和从左面看的形状图.
【解答】解:如图所示:
24.(2020春?肇源县期末)按要求完成下列视图问题
(1)如图(一,它是由6个同样大小的正方体摆成的几何体.将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?
(2)如图(二,请你借助图四虚线网格画出该几何体的俯视图.
(3)如图(三,它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助图四虚线网格画出该几何体的主视图.
【解答】解:(1)如图(一,它是由6个同样大小的正方体摆成的几何体.将正方体①移走后,
新几何体的三视图与原几何体的三视图相比,左视图没有发生改变;
(2)如图1所示,
(3)如图2所示.
25.(2018秋?永安市期末)(1)如图1是由大小相同的小立方块搭成的几何体,请在图2的方格中画出从上面和左面看到的该几何体的形状图.(只需用铅笔将虚线化为实线)
(2)若要用大小相同的小立方块搭一个几何体,使得它从上面和左面看到的形状图与你在图2方格中所画的形状图相同,则搭这样的一个几何体最大需要 9 个小立方块.
【解答】解:(1)如图所示:
(2)搭这样的一个几何体最大需要个小立方块.
故答案为:9.
26.(2018秋?通川区期末)如图是小强用八块相同的小立方体搭成的一个几何体,从正面、左面和上面观察这个几何体,请你在下面相应的位置分别画出你所看到的几何体的形状图(在答题卡上画完图后请用黑色签字笔描图)
【解答】解:三视图如下:
27.(2018秋?张店区期中)小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了 8 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:已知这个长方体纸盒高为,底面是一个正方形,并且这个长方体纸盒所有棱长的和是,求这个长方体纸盒的体积.
【解答】解(1)由图可得,小明共剪了8条棱,
故答案为:8.
(2)如图,粘贴的位置有四种情况如下:
(3)长方体纸盒的底面是一个正方形,
可设底面边长,
长方体纸盒所有棱长的和是,长方体纸盒高为,
,
解得,
这个长方体纸盒的体积为:立方厘米.
28.(2018秋?温江区校级月考)棱长为的正方体,摆成如图所示的形状.
(1)如果这一物体摆放三层,试求该物体的表面积;
(2)依图中摆放方法类推,如果该物体摆放了上下20层,求该物体的表面积.
(3)依图中摆放方法类推,如果该物体摆放了上下层,求该物体的表面积.
【解答】解:(1).
故该物体的表面积为;
(2).
故该物体的表面积为;
(3).
故该物体的表面积为.
1
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
