三角形全等的条件AAS导学案

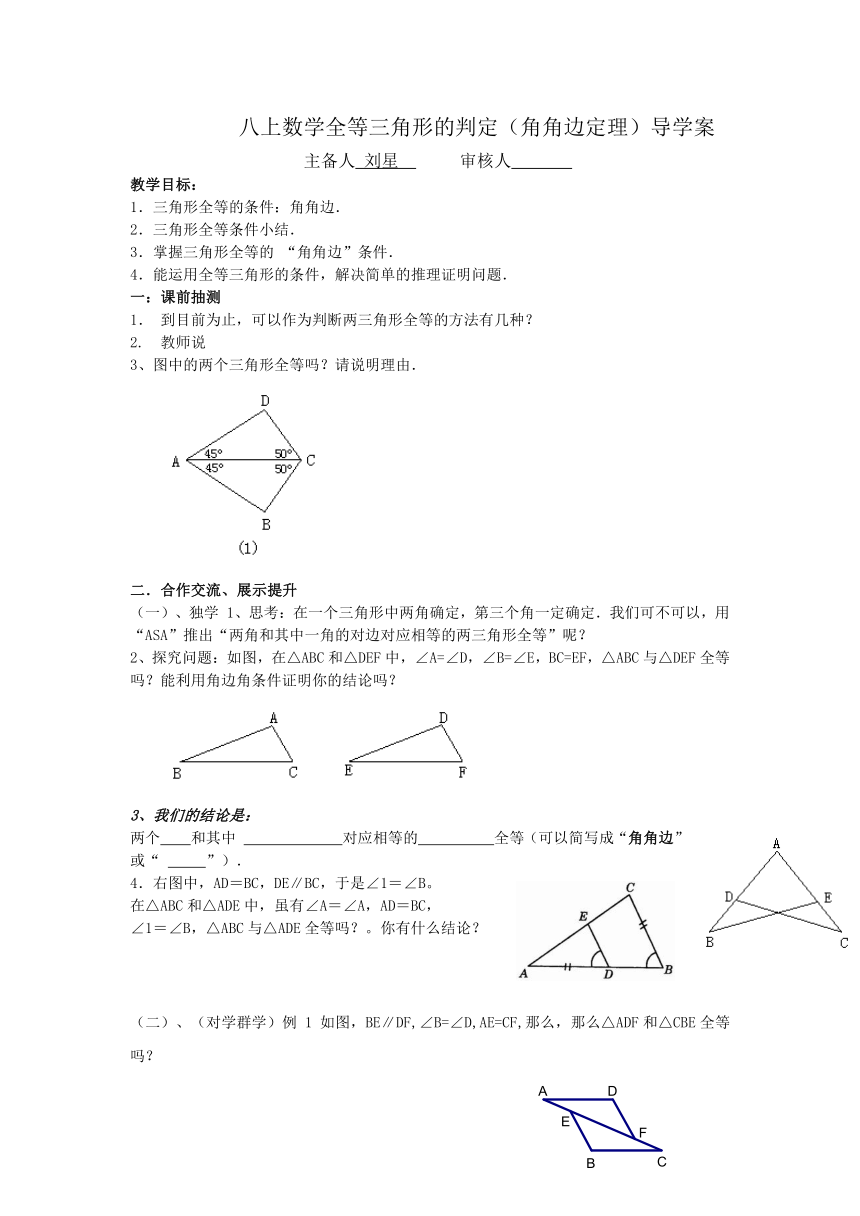
八上数学全等三角形的判定（角角边定理）导学案
主备人 刘星 审核人
教学目标：
1．三角形全等的条件：角角边．
2．三角形全等条件小结．
3．掌握三角形全等的 “角角边”条件．
4．能运用全等三角形的条件，解决简单的推理证明问题．
一：课前抽测
1． 到目前为止，可以作为判断两三角形全等的方法有几种？
2. 教师说
3、图中的两个三角形全等吗？请说明理由．
二．合作交流、展示提升
（一）、独学 1、思考：在一个三角形中两角确定，第三个角一定确定．我们可不可以，用“ASA”推出“两角和其中一角的对边对应相等的两三角形全等”呢？
2、探究问题：如图，在△ABC和△DEF中，∠A=∠D，∠B=∠E，BC=EF，△ABC与△DEF全等吗？能利用角边角条件证明你的结论吗？
3、我们的结论是：
两个 和其中 对应相等的 全等（可以简写成“角角边”或“ ”）．
4．右图中，AD＝BC，DE∥BC，于是∠1＝∠B。
在△ABC和△ADE中，虽有∠A＝∠A，AD＝BC，
∠1＝∠B，△ABC与△ADE全等吗？。你有什么结论？
（二）、（对学群学）例 1 如图，BE∥DF,∠B=∠D,AE=CF,那么，那么△ADF和△CBE全等吗？
例2 已知：△ABC和,BE，分别是对应边AC和边上的高，那么BE和相等吗？
我们的结论：
3、已知：如图中，∠1＝∠2，∠C＝∠D。求证：AC＝AD
三、穿插巩固：
1、至此，我们判定三角形全等的方法：
2、已知一边一角时怎样证明两三角形全等？已知两角呢？．
四、效果检测：
1．（由对学群学第3题改编）已知：如图中，∠1＝∠2，∠3＝∠4。求证：AC＝AD
证明： ∵∠3＝∠4（已知）
∴180°－∠____=180°－∠____， 即∠____=∠_____。
在△ 和△ 中，
　 ∴△ ≌△ （ASA）。
2、如下图，D在AB上，E在AC上，AB=AC，∠B=∠C．求证：AD=AE．
分析：AD和AE分别在△ADC和△AEB中，所以要证AD=AE，只需证明△ADC≌△AEB即可．